鋼彈簧浮置板鋼筋建模計算對比分析

陳真

（北京九州一軌隔振技術有限公司，北京 00070）

1 概述

鋼彈簧浮置板是近幾年國內廣泛應用的一種新型軌道減振降噪結構，國內外學者已對其做了深入研究。[1]但在對浮置板計算時，僅是把浮置板當作單一的混凝土材料，沒有考慮鋼筋的作用，也沒有給出為什么不考慮鋼筋作用的原因。本文詳細對比計算了幾種浮置板內部鋼筋的建模計算結果。

2 浮置板有限元模型的建立

有限元模型的建立是有限元分析的基礎，也是能否得到精確計算結果的關鍵。本文的有限元計算模型包括：直接建立不同情況下的模型、工況約束條件的建立、載荷的施加。

2.1 建立不同計算情況下的有限元模型

根據鋼彈簧浮置板上部有扣件、下部有鋼彈簧、內部鋼筋布置的特點，一次性建立出包含所有部件的有限元模型，在計算時根據計算所考慮的情況去掉不需要的部件。模型中浮置板用的是SOLID185實體單元，鋼筋用的是LINK180桿單元或者是BEAM188梁單元，鋼彈簧和扣件用的是COMBIN14彈簧單元，鋼軌用的是BEAM188梁單元。用于計算簡支靜力載荷和模態的模型見圖1；浮置板內的鋼筋見圖2；用于計算鋼彈簧浮置板模態和軸重載荷的模型見圖3；鋼彈簧浮置板見圖4。

圖1 用于計算簡支靜力載荷和模態的模型

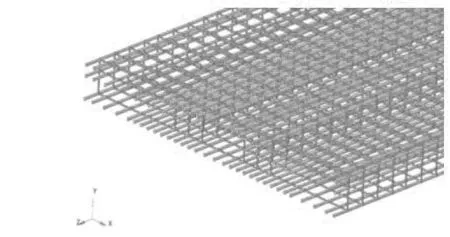
圖2 浮置板內的鋼筋

圖3 用于計算鋼彈簧浮置板模態和軸重載荷的模型

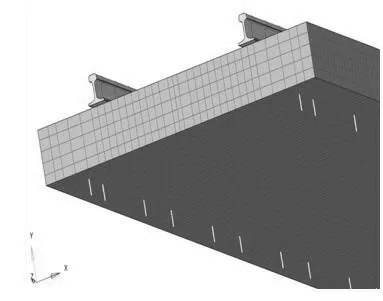
圖4 鋼彈簧浮置板

2.2 模型材料參數

模型的材料參數見表1。鋼軌的截面參數通過導入幾何外形由軟件自動計算。

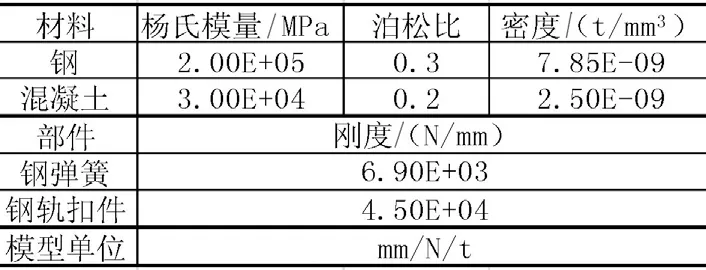
表1 材料參數

2.3 有限元模型邊界約束條件

邊界條件是實際工況在有限元模型上的表現形式。在建立有限元模型的邊界約束條件時，一般需要兩個環節：1）對實際工況條件進行量化；2）將量化后的工況條件定義為有限元模型的邊界條件。

2.3.1 浮置板簡支支撐工況

對浮置板簡支支撐工況計算時，約束浮置板一端的x,y兩個方向自由度和另外一端的x,y,z三個方向的自由度。浮置板簡支約束見圖5。

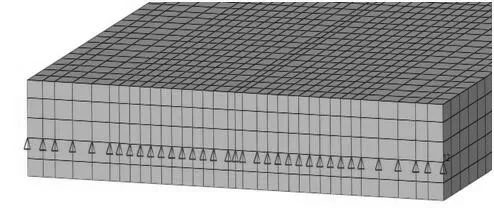
圖5 浮置板簡支約束

2.3.2 鋼彈簧浮置板載荷工況計算

對于此類工況的模型僅約束鋼彈簧底部六個方向的自由度。對于軸重加載僅施加了一個轉向架的載荷值。鋼彈簧的邊界條件見圖6；軸重加載位置見圖7。

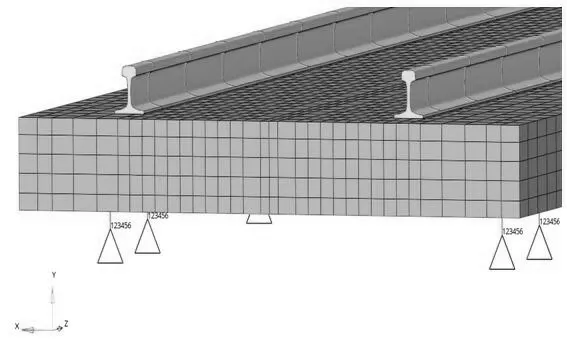
圖6 鋼彈簧的邊界條件

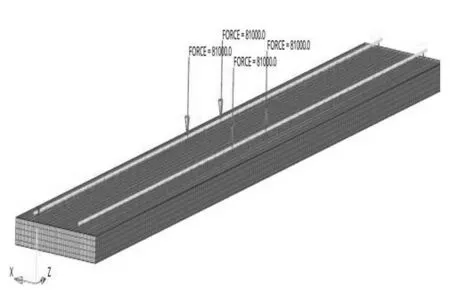
圖7 軸重加載位置

3 有限元計算及結果分析

將建立好的有限元模型施加載荷并進行邊界條件設置后（見圖8），導入ansys求解器中。本次共進行了4大類12種情況的計算。

圖8 浮置板計算示意圖

3.1 浮置板簡支支撐靜力載荷計算

此類計算為考量大跨度下浮置板的受力，計算時，浮置板內有無鋼筋及鋼筋單元類型不同都會影響計算結果的精度。簡支梁集中載荷受力見圖9。

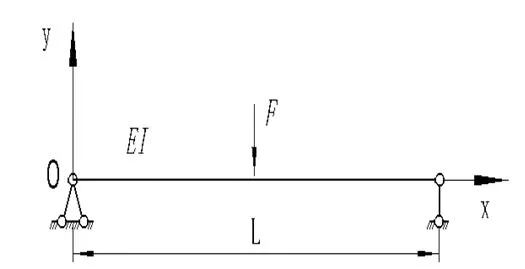
圖9 簡支梁集中載荷受力圖

依據材料力學：簡支梁跨中集中載荷的最大撓度計算公式為：

式中：

P—集中載荷，P=3500N；

E—混凝土彈性模量，對于混凝土，E=30 000MPa ；

I—浮置板截面慣性矩，I=8.49emm4；

L—浮置板的長度，L=25 000mm 。

將以上數值代入公式得到理論最大撓度值為Ymax=4.492mm 。

簡支梁集中載荷變形云圖見圖10；浮置板簡支支撐集中載荷計算結果見表2。

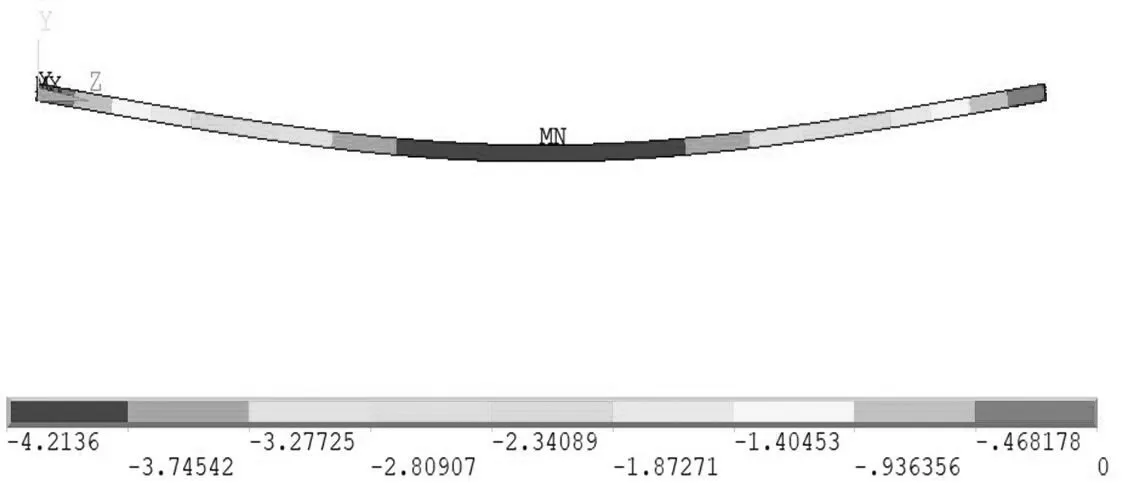
圖10 簡支梁集中載荷變形云圖

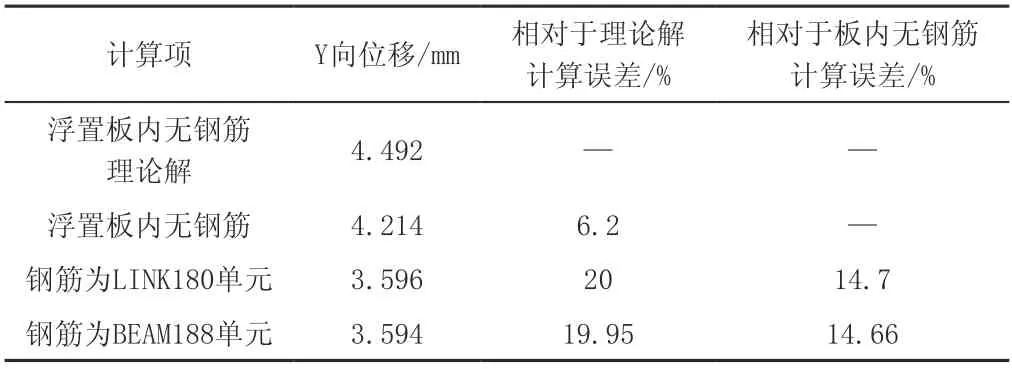
表2 浮置板簡支支撐集中載荷計算結果匯總

從表2的對比數據可知，對大跨度簡支支撐的浮置板在計算時不考慮鋼筋，對計算的結果影響較大。計算時鋼筋建模采用LINK單元和BEAM單元對計算結果幾乎沒有影響。

3.2 浮置板簡支支撐模態計算

本文計算均質等截面細直梁的橫向彎曲振動。假定條件為1）梁具有縱向對稱平面；2）梁的長度與截面高度之比大于10；3）忽略剪切變形和轉動慣量的影響。

設梁的長度為L，單位長度的質量P及抗彎剛度EI均為常數，建立坐標系。

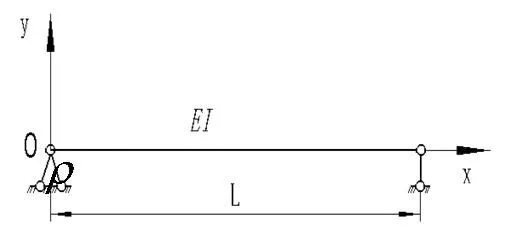
在梁上距左端x處取微元段dx，在任意瞬時t，剪力為Q(x,t)，彎矩為M(x,t)，均布載荷為p(x,t)，在微元段的橫向位移可用y(x,t)表示。按其受力情況，微元段沿y方向的運動方程為：

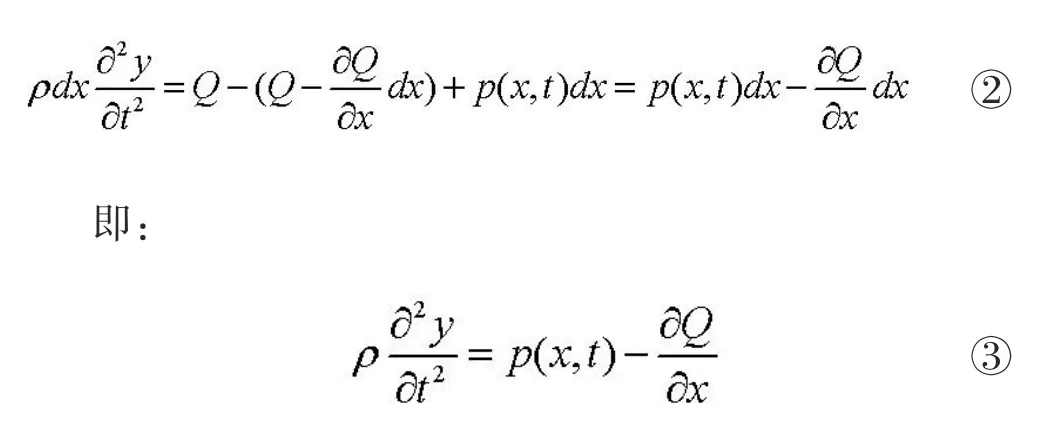
由微元右端截面力矩平衡方程可以得到：

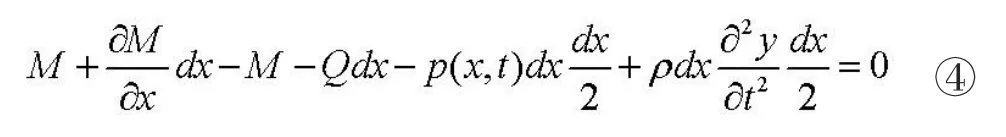
略去二階微量，則有：

由材料力學中的平面假設條件，可以得到彎矩與撓度曲線的關系，即：

將式④、⑤代入③，得：

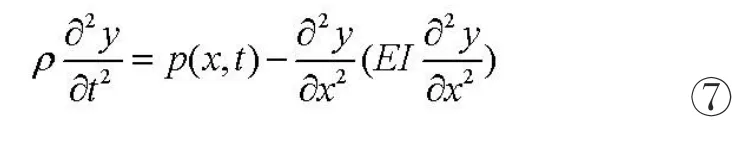
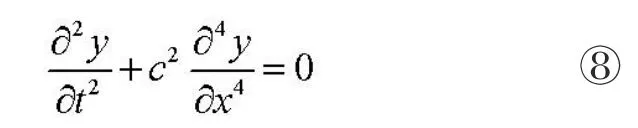
對方程⑦通過分離變量、引入雙曲函數和歐拉公式求其通解為：

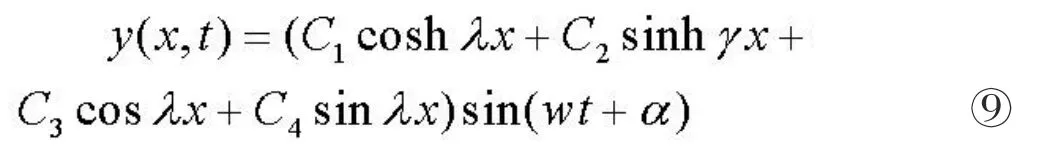
對于簡支梁其端部處的撓度與彎矩都為零，即邊界條件：

將邊界條件代入式⑦可得簡支梁的彎曲振動的頻率解為：

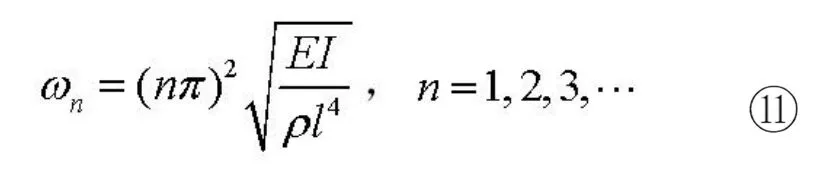
本文僅計算第一階彎曲振動頻率，其中：

E—混凝土彈性模量，對于混凝土E=30 000MPa ；

I—浮置板截面慣性矩，I=8.45e9mm4；

L—浮置板的長度，L=25 000mm；

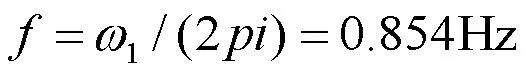
浮置板簡支支撐第一階模態見圖11；浮置板簡支模態計算結果見表3。

圖11 浮置板簡支支撐第一階模態

表3 浮置板簡支模態計算結果匯總

從表3的對比數據可知，有限元計算浮置板頻率值和理論計算值相差很小，在工程誤差范圍內。浮置板內有鋼筋和無鋼筋的頻率值對比誤差值也很小，在計算模態頻率值時，可以不考慮浮置板內鋼筋。

3.3 鋼彈簧浮置板模態計算

浮置板簡支支撐第一階模態見圖12；鋼彈簧浮置板模態計算結果見表4。

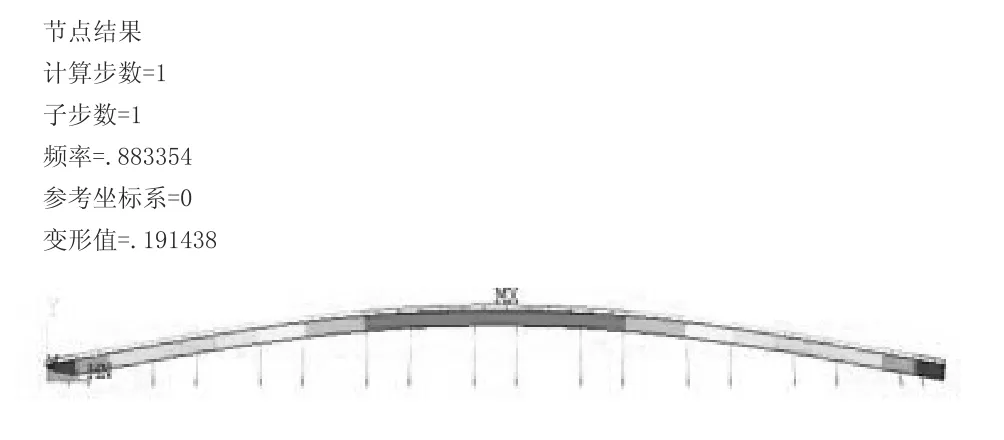
圖12 剛彈簧浮置板簡支支撐第一階模態

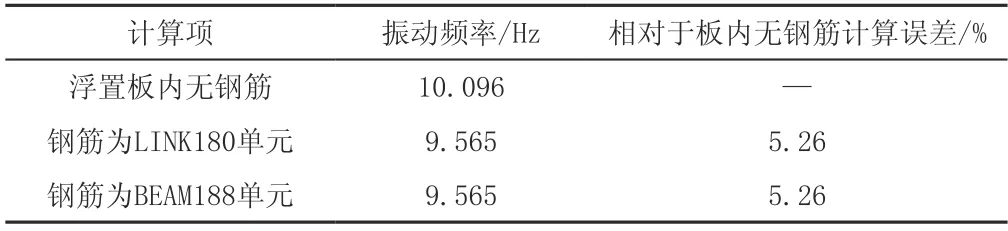
表4 鋼彈簧浮置板模態計算結果匯總

從表4的對比數據可知，浮置板內有鋼筋和無鋼筋對其頻率的計算有一定的影響，頻率結果值相差5.26%。鋼筋用LINK單元和BEAM單元建模對計算結果沒有影響。

3.4 鋼彈簧浮置板軸重載荷計算

鋼彈簧浮置板軸重載荷第一階模態見圖13；鋼彈簧浮置板軸重載荷計算結果見表5。

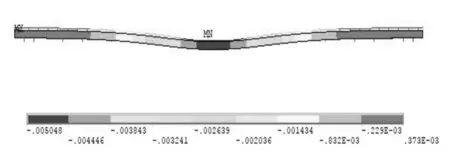
圖13 鋼彈簧浮置板軸重載荷第一階模態

表5 鋼彈簧浮置板軸重載荷計算結果匯總

從表5中計算結果可知，浮置板內有無鋼筋對于鋼彈簧浮置板系統的變形計算結果影響很小，誤差僅為2.42%。而鋼筋采用LINK單元和BEAM單元建模對計算結果無影響。

4 結語

（1）通過對浮置板簡支支撐靜力載荷的分析可知，對于大跨度的簡支支撐的浮置板計算其撓度時，需要考慮內部鋼筋的作用。而底部有鋼彈簧彈性支撐的浮置板在軸重載荷作用下，板內有無鋼筋撓度的計算結果相差很小，均在工程誤差范圍內，因此在對浮置板計算時，可以不考慮內部鋼筋的作用。

（2）無論是大垮度簡支支撐的浮置板還是底部有鋼彈簧彈性支撐的浮置板，計算浮置板內部有無鋼筋，對模態振型和頻率值影響都非常小。

（3）對比板內鋼筋的建模采用LINK單元或者是BEAM單元計算的結果，兩者的值幾乎一致，在后續計算時，可根據情況選用其中的一個。