限制失真的網格參數化方法

蔡興泉 孫辰 葛亞坤

摘 要：針對當前網格參數化效率較低、映射失真較嚴重的問題，提出一種限制失真的網格參數化方法。首先，預處理原始網格模型。輸入原3D網格模型，采用Half-Edge數據結構來重新組織網格并切割網格模型產生相應的切縫;構建Tutte映射把3D網格映射到一個2D凸多邊形域，即構建2D網格模型。然后，進行限制失真的網格參數化計算。將Tutte映射后的2D網格模型作為限制失真計算的初始數據，建立相對于原3D模型網格的失真度量函數;求得該度量函數的最小值點，即為映射后的網格坐標集合;將映射后的網格作為限制失真映射的輸入網格，設定迭代終止條件，循環迭代直至迭代結束，得到收斂的最優網格坐標;在計算映射失真度時，針對等距映射失真采用Dirichlet能量函數度量，針對共形映射失真采用盡可能等距（MIPS）能量函數度量;在求解映射失真度量函數的最小值點時采用代理函數法結合組合牛頓法的最優解方法。最終，實現了該方法并開發了一個原型系統。在原型系統中，分別設計了限制等距失真和限制共形失真的網格參數化實驗，對程序執行時間和失真能量下降情況進行了統計和對比，提供了相應的紋理映射效果展示。實驗數據表明，所提出的方法執行效率高、映射失真能量下降快，最優值收斂質量穩定;紋理映射時紋理著色均勻、布局緊致、線條均勻，符合實際應用的標準。

關鍵詞：網格參數化;限制失真;等距映射;共形映射;能量函數;最優坐標點

中圖分類號： TP391.9

文獻標志碼：A

Abstract：Aiming at the low efficiency and serious mapping distortion of current mesh parameterization， a mesh parameterization method with limiting distortion was proposed. Firstly， the original mesh model was pre-processed. After inputting the original 3D mesh model， the Half-Edge data structure was used to reorganize the mesh and the corresponding seams were generated by cutting the mesh model. The Tutte mapping was constructed to map the 3D mesh to a 2D convex polygon domain， that is to construct the 2D mesh model. Then， the mesh parameterization calculation with limiting distortion was performed. The Tutte-mapped 2D mesh model was used as the initial data for limiting distortion calculation， and the distortion metric function relative to the original 3D model mesh was established. The minimum value points of the metric function were obtained， which form the mapped mesh coordinate set. The mapped mesh was used as the input mesh to limit the distortion mapping， and the iteration termination condition was set. The iteration was performed cyclically until the termination? condition was satisfied， and the convergent optimal mesh coordinates were obtained. In calculating the mapping distortion， the Dirichlet energy function was used to measure the isometric mapping distortion， and the Most Isometric Parameterizations （MIPS） energy function was used for the conformal mapping distortion. The minimum of the mapping distortion energy function was solved by proxy function combining assembly-Newton method. Finally， this method was implemented and a prototype system was developed. In the prototype system， mesh parameterization experiments for limiting isometric distortion and limiting conformal distortion were designed respectively， statistics and comparisons of program execution time and distortion energy falling were performed， and the corresponding texture mapping effects were displayed. Experimental? results show that the proposed method has high execution efficiency， fast falling speed of mapping distortion energy and stable quality of optimal value convergence. When texture mapping is performed， the texture is evenly colored， close laid and uniformly lined， which meets the practical application standards.Key words：? mesh parameterization; limiting distortion; isometric mapping; conformal mapping; energy function; optimal coordinate point

0 引言

網格參數化是數字幾何處理中的熱點和難點[1]。網格參數化的任務是將三維空間的網格映射到二維空間，稱為平面參數化。網格參數化可用在紋理映射、網格變形、網格編輯等領域。

最初，數學家Tutte[2]證明了網格模型任何一個頂點的坐標可表示為其鄰接頂點坐標的加權組合，提出了邊界域凸組合映射，為網格參數化提供了理論基礎。在映射計算時，容易產生失真，如三角網格的邊長可能會變，三角網格的內角可能會變。三角網格的邊長在映射前后發生變化稱為等距失真;三角網格的內角在映射前后發生變化稱為共形失真。但是，Tutte算法在映射的過程中并沒有對映射失真進行約束。Hormann等[3]提出了保證無網格翻轉的映射，以保證網格不發生翻轉并降低映射產生的失真。Lipman[4]于2012年提出了限定失真的映射，設定了失真閾值，從而進一步減少映射帶來的失真，并拓寬了網格參數化的應用范圍。受該方法啟發，本文主要研究限制失真的網格參數化方法。

在限制失真時，需要構建映射失真度量函數。關于等距失真映射，Hormann提出了盡可能等距（Most Isometric Parameterizations， MIPS）能量函數，Alexa等[5]提出盡可能剛體（As Rigid As Possible， ARAP）能量函數，Smith等[6]于2015年提出了對稱狄利克雷（Symmetric Dirichlet， Dirichlet）能量函數。關于共形失真映射，Sorkine等[7]提出了比值能量函數，隨后又在文獻[8]中提出了盡可能相似（As Similar As Possible， ASAP）能量函數。綜合考慮能量函數的度量精確性和易優化性，本文選用狄利克雷能量函數作為等距映射的失真度量函數，選用盡可能等距能量函數作為共形映射的失真度量函數。

映射失真函數的最優坐標解依賴于數值最優化方法。文獻[9]中常用的數值優化方法有梯度下降法、牛頓法、擬牛頓法等。失真度量函數通常是非線性非凸的，有些能量函數帶有約束項。因此，需要改進這些最優化方法以解決最優坐標快速求解問題。對于梯度下降法，主要是根據原函數的一階導數確定下降方向。Kovalsky等[10]于2016年提出利用網格的Laplacian矩陣確定能量函數初始的下降方向。該方法在迭代前期失真下降較快，但是由于一階導數缺少自由度之間的耦合信息，導致在迭代后期收斂質量和效率較差。Rabinovich等[11]于2018年提出了代理函數方法，將難以優化求解的度量函數轉化為易優化的簡單函數，利用局部全局（Local-Global）的思想結合代理函數的一階導數信息確定下降方向。該方法在最優值求解迭代初期，能量下降速度很快。對于牛頓法，主要利用能量函數的Hessian矩陣確定原函數下降方向，要保持Hessian的正定。為此，Teran等[12]提出了投影牛頓法，對Hessian矩陣進行特征值分解，將非正的特征值設定為較小的正值，保持了矩陣的正定，從而保持了最優解的穩定性。該方法在實際求解過程中其計算過于復雜，時間復雜度表現較差。Shtengel等[13]提出組合牛頓法，對失真函數進行局部凸化，把非凸函數轉化為凸函數，并保持Hessian正定，保證了最優解的收斂穩定性和求解的效率。對于擬牛頓法，則介于梯度下降法和牛頓法之間，主要思想是利用一階導數信息來近似二階導數確定下降方向。Nocedal提出了低內存占用的擬牛頓法，此方法解決與初始解的選取無關的優化問題的能力較弱。為了在最優坐標解的求解中充分利用各種優化方法的優勢，當初始解離最優解距離較遠時，用代理函數法求解最優坐標;在當前解離最優解距離較近時，用組合牛頓法求解最優坐標。

當前網格參數化算法效率較低、映射失真較嚴重，本文主要研究限制失真的網格參數化方法。首先預處理原始網格模型，然后進行限制失真的網格參數化計算。

1 預處理原始網格模型

在進行網格參數化運算前，需要預處理原始網格模型。首先，輸入的是原網格模型OriginalModel。該網格模型是以頂點集和面片集為存儲格式的3D網格模型。這種3D網格模型是網格建模常用的存儲結構;然后，采用OpenMesh網格處理庫中高效的Half-Edge數據結構來重新組織網格數據;接著，切割網格模型，產生Seam，即在模型上產生相應的切縫;最后，利用切割好的模型構建Tutte映射，把3D網格映射到一個2D凸多邊形域，即2D網格模型。

1.1 切割網格模型

輸入原網格模型，利用Half-Edge數據結構來重新組織網格數據后，對原3D網格模型進行切割，產生切縫。目的是將虧格大于1、有多個洞的模型轉化為虧格為0、無洞的片狀拓撲模型。

對原3D網格模型進行切割時，有兩種方法，即Seamster網格切割法和幾何圖像法。Seamster網格切割法根據3D模型的高曲率點和模型中不可視區域確定切線，采用最小Steiner樹算法盡量縮短切縫長度;幾何圖像法采用網格參數化與網格切割交替迭代，將參數化失真嚴重的點作為下次切割的切點。

在實現時，本文用這兩種方法完成網格模型切割。這兩種方法都是運用代數拓撲理論保證切線能把任意虧格的模型轉化為虧格為0的開網格。

1.2 構建Tutte映射

由于Tutte映射既可以保證網格不發生翻轉，又可以保證映射后的網格不發生交叉，即可保證雙射。因此，本文在完成切割網格模型后，對模型構建Tutte映射，為后續參數化計算做好準備。

對模型構建Tutte映射時，首先將網格模型的邊界頂點集序列組成凸多邊形的邊界頂點集序列。邊界頂點較多，因此所圍成的凸多邊形邊界近似一個圓。本文在實現時，將凸多邊形邊界頂點集序列依次平均分布在一個單位圓上。

然后，解重心坐標映射方程（1）得到此凸多邊形區域所有內點的坐標。

這些內點的坐標即構建Tutte映射后的2D網格頂點的坐標。

重心坐標映射方程把內點坐標的求解運算轉化為線性系統的計算，也就是求解兩個線性系統Au=和Av=。在方程（1）中，向量u和向量v代表凸多邊形域所有內點的（u， v）坐標，向量和向量代表凸多邊形域所有邊界點的（u， v）坐標。

2 限制失真的網格參數化計算

網格參數化計算最基本的要求是：保證映射計算后的2D網格模型無網格翻轉，即映射前后兩個階段的2D網格的三個頂點順序均按逆時針順序排列。在映射計算時，容易產生失真，包括等距失真和共形失真。在網格參數化計算的過程中，嚴格消除等距失真或共形失真是難以做到的，但是，采用限制失真的方法在映射計算中盡量減少失真是可行的。

本文采用限制失真的網格參數化計算，具體步驟如下：

Step1：將Tutte映射計算后的2D網格作為限制失真計算的初始數據，建立相對于原3D模型網格OriginalModel的失真度量函數;

Step2：利用失真度量函數求得該度量函數的最小值點，即為映射后的網格坐標集合;

Step3：將映射后的網格作為限制失真映射的輸入網格，設定迭代終止條件，循環迭代Step1～2，直至迭代結束，得到收斂的最優網格坐標。

2.1 構建失真度量函數

網格參數化的處理過程實際上是每個網格的映射過程。該映射類型為分段線性映射。該映射定義在每個三角網格上，表達式如式（3）所示：

其中：J是映射函數的Jacobian二階矩陣，決定了映射的性質;b是位移平移量，為一個常量向量，在實際使用時一般用零向量代替;x、 y是映射前的網格頂點坐標;u和v是映射后的網格頂點坐標。無網格翻轉的約束條件為J的行列式值大于0。

計算映射失真度需要建立失真刻畫精確、計算簡單、容易求得最小值的失真度量函數。鑒于此，采用Dirichlet能量函數度量等距映射失真，采用MIPS能量函數度量共形映射失真。

2.1.1 基于Dirichlet能量函數度量的等距映射

等距映射保持三角網格的邊長在映射前后不變。由于Jacobian矩陣決定了變換的幾何性質，J的特征值決定了J的性質，故能量函數主要以J的特征值為變量。Dirichlet能量函數描述如式（4）所示：

共形映射保證映射前后網格的內角不變，即保證相似性。MIPS能量函數最初用來約束等距映射失真，但是其約束目標主要是σ1=σ2，更傾向于共形映射的約束目標，對等距失真的約束效果不如Dirichlet函數，所以用它作為共形映射的失真能量函數。此函數同樣具有計算量小、度量精確、魯棒性強等特點，MIPS能量函數描述如式（6）所示：

2.2 基于能量函數求解最優坐標點

映射失真度量函數的最小值點是映射后網格的最優坐標點。考慮到數值最優化方法各有優勢，采用代理函數法結合組合牛頓法的最優解方法。為了加速失真能量的下降，在前期失真能量值高的迭代步引入了參考網格，用參考網格代替原3D模型網格建立能量函數;接著利用此最優解方法求解映射后最優坐標，優化方法采用全局優化。通過數學理論分析結合實驗數據統計得出實驗的控制參數，參數具有普遍意義，對于不同的數據集有良好的魯棒性。

當失真能量下降率大于0.1時采用代理函數法;當能量下降率小于0.1大于0.01時采用組合牛頓法;當能量下降率小于0.001時，就不再建立參考網格，直接用組合牛頓法迭代得出最優解。對于Dirichlet能量函數，當能量梯度范數小于1×10-6時迭代停止;對于MIPS能量函數，當能量梯度范數小于1×10-4時迭代停止，最大迭代步數為100。

2.2.1 基于梯度下降的代理函數最優坐標解法

代理函數法的主要思想是通過優化比能量函數更易優化的代理能量函數來間接優化能量函數，而代理能量的優化可以看作盡可能剛體失真能量的局部全局優化方法的推廣。該方法的代理函數P（x）寫成式（8）的形式：

其中：矩陣U和V是當前Jacobian矩陣做特征值分解后的兩個旋轉矩陣;k指當前第k次迭代;λ取1×10-4;A表示網格的面積; f表示每個三角網格;‖·‖表示求矩陣的歐氏范數;SJ是Jacobian矩陣的特征值矩陣;D（SJ）是失真能量函數;

Λ為一個常量矩陣，根據失真能量函數確定。對于Dirichlet能量函數，旋轉矩陣的特征值矩陣SΛ兩個值均為1;對于MIPS能量函數，SΛ兩個值均為σ1 σ2。

最后利用函數的一階導數求得代理函數的下降方向。

2.2.2 組合牛頓最優坐標解法

組合牛頓法的主要思想是把非凸的失真能量函數做局部凸化轉化為凸函數，再用牛頓法得出函數的下降方向。失真能量函數可寫成復合函數，如式（11）所示：

最后利用所求得的Hessian矩陣確定能量函數的下降方向。

為求解能量函數的下降步長，首先根據能量函數的下降方向確定所有網格發生翻轉時的步長，并取所有步長的最小值作為最大步長;接著根據最大步長用基于Armijo準則的回溯算法求得失真函數的實際下降步長;最后結合能量函數的下降方向和下降步長得出映射后的網格坐標，即本次迭代后的網格坐標。

2.2.3 建立參考網格

遞進參數化的思想主要是建立參考網格代替原模型網格。本文在實現遞進參數化的計算時，具體步驟如下：

Step1：首先設定一個失真閾值，然后根據前一個迭代步結束后生成的模型網格，再結合原模型網格建立能量函數，最后根據能量函數確定映射函數Jacobian矩陣的特征值，再結合原模型網格計算得到參考網格;

Step2：首先由前一個迭代步產生的模型網格結合當前的參考網格建立能量函數，然后求解能量函數的最優坐標值得出當前迭代步的模型網格;

Step3：設定迭代終止條件，循環迭代Step1和Step2，直至迭代結束，得到收斂的最優網格坐標。

遞進參數化的原理是，較高的失真能量會影響最優解的求解速度。采用建立參考網格的方法，每次優化一個較小的失真，可以提高優化的效率。特別在選用了產生高失真能量值的能量函數，或迭代初始點離最優解距離較遠時使用效果更佳。但此方法會增加內存的開銷，故迭代次數不宜過多，當失真能量降到一個較低的水平時，此方法沒有明顯優勢。對Dirichlet能量約束的等距映射，首先采用指數插值法讓失真能量值等于200，方程如式（15）所示：

然后對每個網格用牛頓求根法計算t值。接著對所有網格取t的最小值，以最小值作為參數求得新的Jacobian矩陣特征值，最后根據特征值求出每個參考網格的頂點。對MIPS能量約束的共形映射，直接采用線性插值法根據約束目標迭代讓特征值相互接近，失真能量值小于3時迭代停止，取當前的特征值，以此求得參考網格的頂點坐標。

3 實驗與結果分析

本文設計并實現了所提出的限制失真的網格參數化方法，并開發了一個驗證系統。本文實驗中所采用的輸入模型選自法國INRIA的Unwarpped Meshes網格模型庫和中國科技大學的Disk-topology Meshes網格模型庫。實驗中的牛、兔、手掌模型取自Unwarpped Meshes庫，魚、人、玩偶模型取自Disk-topology Meshes網格模型庫。牛模型網格數量為69451個，兔模型網格數量為34504個，手掌模型網格數量為72598個，魚模型網格數量為16428個，人模型網格數量為19012個，玩偶模型網格數量為25082個。實驗硬件環境為Intel Core i7 7700 HQ，2.8GHz，四核心八線程CPU，Samsung 2400MHz 8GB內存，NVIDIA 1050 Ti 4GB顯卡，Windows 10 操作系統的筆記本電腦。在實現驗證系統時，采用C++作為編程語言，采用Visual Studio 2017作為開發工具。在進行相關稀疏矩陣和稀疏向量的計算時，利用Eigen計算庫完成。

網格參數化計算非常注重運行效率和映射失真的下降速度。失真分為等距失真和共形失真，因此，本文設計了限制等距失真映射實驗和限制共形失真映射實驗。兩個實驗均進行了較為客觀的實驗數據統計和較為主觀的紋理映射效果展示。實驗數據統計包括程序執行時間對比、失真能量下降情況對比等。在統計程序執行時間數據時，分別對牛、兔、手掌、魚、人、玩偶等模型進行1000次網格參數化計算，統計時間，最終求得平均值。在統計失真能量下降情況數據時，對每個模型迭代計算，統計相應的失真能量值。在紋理映射的實驗中，利用OpenGL紋理映射函數綁定參數化后的網格坐標，即原模型的紋理坐標，從而生成OriginalModel模型的紋理貼圖。

3.1 限制等距失真的網格參數化實驗

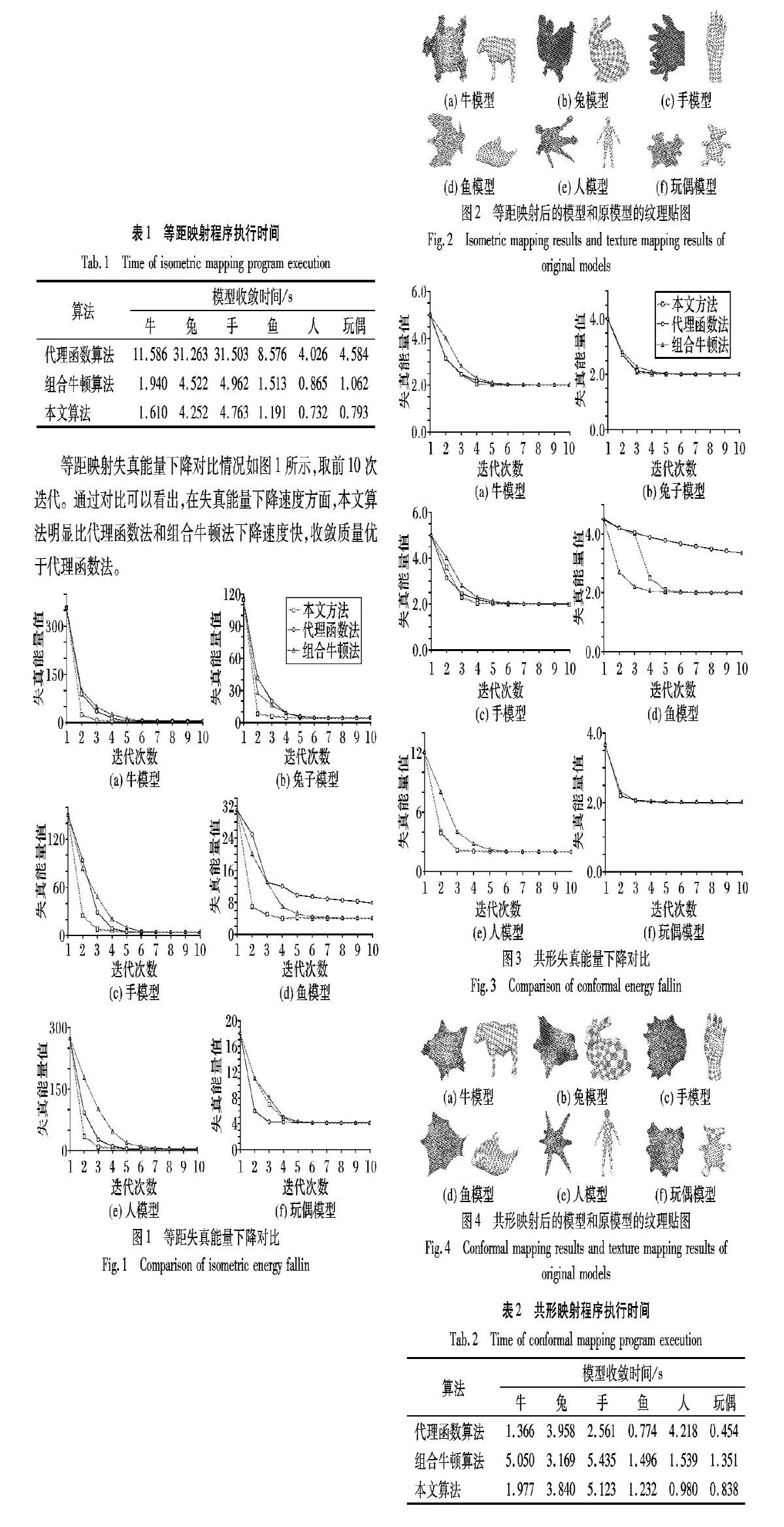
限制等距失真的網格參數化執行時間如表1所示。

從表1可看出：在處理相同模型時，本文算法程序執行時間明顯比代理函數算法和組合牛頓算法短。

等距映射失真能量下降對比情況如圖1所示，取前10次迭代。通過對比可以看出，在失真能量下降速度方面，本文算法明顯比代理函數法和組合牛頓法下降速度快，收斂質量優于代理函數法。

3.2 限制共形失真的網格參數化實驗

限制共形失真的網格參數化執行時間如表2所示。從表2可看出：在處理相同模型時，本文算法的程序執行時間明顯比組合牛頓法的短，但比代理函數法稍長。共形映射失真能量下降對比情況如圖3所示，取前10次迭代。通過對比可以看出，在失真能量下降速度方面，本文算法比代理函數法和組合牛頓法下降速度快，收斂質量優于代理函數法。模型共形映射后的結果和紋理貼圖效果如圖4所示。可以看出各區域紋理著色均勻，不同區域的紋理圖案具有相似性。

3.3 實驗結果分析

對映射實驗的統計數據進行分析。對于等距映射，能量函數每一項均為平方項，所以在映射失真時所產生的能量值較大，遞進式參數化策略在迭代前期能充分地發揮其優勢。采用代理函數法結合組合牛頓的方法使得求解效率得到提高，既能發揮基于梯度下降的代理函數方法在前期迭代的快速下降的優勢，又能發揮出牛頓法的二次收斂性和收斂穩定性。對于共形映射，由于所選用的失真能量函數每一項是比值項，所以產生的失真能量值相對較小，建立參考網格需要一定的程序時間和內存空間，所以最優坐標點的求解效率比等距映射低，但是相對于不采用參考網格的方法在程序時間上和優化結果上仍有優勢。值得注意的是，在迭代前期單獨使用代理函數法優化效率較高，但隨著迭代次數增加，當前解逐漸靠近最優解時收斂速度很慢。

從紋理映射效果上直觀分析，對于等距映射，映射產生的紋理效果布局緊致，紋理條紋呈現均勻，但在局部區域出現角度失真。對于共形映射，紋理布局在局部區域呈現松弛，出現距離失真，但是不同區域的相似性得到了體現，各區域紋理著色均勻，對于角度的失真約束更加可觀。在實際應用中，在對距離失真和紋理的均勻性要求嚴格的情況下，建議采用等距映射的參數化方法，在對角度失真和紋理的相似性要求嚴格的情況下，建議采用共形映射參數化。經實驗分析，該算法的魯棒性強，參數化結果對參數的調整很穩定。

4 結語

針對當前網格參數化效率較低、映射失真較嚴重的問題，本文提出了一種限制失真的網格參數化方法。首先，預處理原始網格模型。然后，進行限制失真的網格參數化計算。在計算映射失真度時，采用Dirichlet能量函數度量等距映射失真;采用MIPS能量函數度量共形映射失真。在求解映射失真度量函數的最小值點時，采用代理函數法結合組合牛頓法的最優解方法。最終設計并實現了該限制失真的網格參數化方法，開發了一個驗證系統，分別設計了限制等距失真和限制共形失真的網格參數化實驗。實驗數據表明，本文方法執行效率高，映射失真能量下降快，最優值收斂質量穩定;紋理映射時，紋理著色均勻、布局緊致、線條均勻、符合實際應用的標準。該方法可用在紋理映射、網格變形、網格編輯等領域。

下一步研究工作包括將本文方法擴展，應用于二維網格模型變形、三維網格模型變形、網格編輯、形狀插值、網格質量提升等工作中。

參考文獻（References）

[1] 郭鳳華， 張彩明， 焦文江. 網格參數化研究進展[J]. 軟件學報， 2016， 27（1）： 112-135（GUO F H， ZHANG C M， JIAO W J. Research progress on mesh parameterization[J]. Journal of Software， 2016， 27（1）： 112-135）.

[2] TUTTE W T. How to draw a graph[J]. Proceedings of the London Mathematical Society， 1963， 3（1）： 743-767.

[3] HORMANN K， GREINER G. MIPS： an efficient global parameterization method[EB/OL]. [2019-01-10]. https：//pdfs.semanticscholar.org/02e4/f09c9a6d0d770d31c9289d30b7b4e9b5d974.pdf.

[4] LIPMAN Y. Bounded distortion mapping spaces for triangular meshes[J]. ACM Transactions on Graphics， 2012， 31（4）： 108.

[5] ALEXA M， COHEN-OR D， LEVIN D. As-rigid-as-possible shape interpolation[C]// Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New York： ACM， 2000： 157-164.

[6] SMITH J， SCHAEFER S. Bijective parameterization with free boundaries[J]. ACM Transations on Graphics， 2015， 34（4）： 70.

[7] SORKINE O， COHEN-OR D， GOLDENTHAL R. Bounded-distortion piecewise mesh parameterization[C]// Proceedings of the 2002 Conference on Visualization. Piscataway： IEEE， 2002： 355-362.

[8] SORKINE O， ALEXA M. As-rigid-as-possible surface modeling[C]// Proceedings of the 5th Eurographics Symposium on Geometry Processing. Aire-la-Ville， Switzerland： Eurographics Association， 2007： 109-116.

[9] NOCEDAL J， WRINGT S J. Numerical Optimization[M]. Berlin： Springer， 1999： 1-10.

[10] KOVALSKY S Z， GALUN M， LIPMAN Y. Accelerated quadratic proxy for geometric optimization[J]. ACM Transactions on Graphics， 2016， 35（4）： 134.

[11] RABINOVICH M， PORANNE R， PANOZZO D， et al. Scalable locally injective maps[J]. ACM Transactions on Graphics， 2017， 36（4）： 37a.

[12] TERAN J， SIFAKIS E， IRVING G， et al. Robust quasi static finite elements and mesh simulation[C]// Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. New York： ACM， 2005： 181-190.

[13] SHETENGEL A， PORANNE R， SORKINE-HORNUNG O， et al. Geometric optimization via composite majorization[J]. ACM Transactions on Graphics， 2017， 36（4）： 38.

[14] SHEFFER A， HART J C. Seamster： inconspicuous low-distortion texture seam layout[C]// Proceedings of the 2002 Conference on Visualization. Piscataway： IEEE， 2002： 291-298.

[15] GU X F， STEVEN J G， HOPPE H. Geometry images[J]. ACM Transactions on Graphics， 2002， 21（3）： 355-361.

[16] FLOATER M S. One-to-one piecewise linear mappings over triangulations[J]. Mathematics of Computation， 2003， 72（242）： 685-696.

[17] LIU L， YE C， NI R， et al. Progressive parameterizations[J]. ACM Transations on Graphics， 2018， 37（4）： 41.

[18] AIGERMAN N， LIPMAN Y. Injective and bounded distortion mappings in 3D[J]. ACM Transactions on Graphics， 2013， 32（4）： 106.

[19] FU X， LIU Y， GUO B. Computing locally injective mappings by advanced MIPS[J]. ACM Transactions on Graphics， 2015， 34（4）： 71.

[20] WEBER O， ZORIN D. Locally injective parameterization with arbitrary fixed boundaries[J]. ACM Transactions on Graphics， 2014， 33（4）： 75.

[21] ZHU Y， BRIDSON R， KAUFMAN D M. Blended cured quasi-newton for distortion optimization[J]. ACM Transactions on Graphics， 2018， 37（4）： 40.

[22] RODOL E， LHNER Z， BRONSTEIN A M， et al. Functional maps representation on product manifolds[J]. Comouter Graphics Forum， 2019， 38（1）： 678-689.