大跨度屋蓋結(jié)構(gòu)平均風(fēng)壓和脈動(dòng)風(fēng)壓研究

任超洋，尤本祥，宋志強(qiáng)，孫遠(yuǎn)辰，溫阿強(qiáng)

(中國十七冶集團(tuán)有限公司, 安徽 馬鞍山 243000)

在工程實(shí)際中大跨度空間結(jié)構(gòu)建筑得到了十分廣泛的應(yīng)用，其發(fā)展速度相對以前加快，如我國在2008年奧運(yùn)會(huì)籌備期間已經(jīng)建好了包括“鳥巢”“水立方”等舉世聞名的大跨度空間結(jié)構(gòu)建筑。大跨度結(jié)構(gòu)是一種新穎的建筑結(jié)構(gòu)形式[1]，通常跨度在30 m以上的建筑統(tǒng)稱為大跨度建筑，其特點(diǎn)主要是質(zhì)量輕、阻尼比小、內(nèi)部可用空間較大、自振頻率低且柔度較大，主要應(yīng)用在展覽館、火車站、飛機(jī)場、大會(huì)堂等大型公共建筑上。目前對于大跨度屋蓋結(jié)構(gòu)的風(fēng)荷載研究已取得大量數(shù)據(jù)，但還不能像高層結(jié)構(gòu)和高聳結(jié)構(gòu)那樣在《規(guī)范》中給出一個(gè)具有代表性的風(fēng)荷載分布形式。大跨度空間結(jié)構(gòu)建筑的屋面平均風(fēng)荷載的獲取較為簡單，研究的關(guān)鍵部分在于如何獲取其脈動(dòng)部分的風(fēng)壓。20世紀(jì)以來，多以現(xiàn)場實(shí)測和風(fēng)洞試驗(yàn)獲得數(shù)據(jù)，隨著計(jì)算機(jī)技術(shù)的日漸成熟，利用數(shù)值方法獲得數(shù)據(jù)的方法已經(jīng)日趨流行。文獻(xiàn)[2]通過現(xiàn)場實(shí)測方法對Rugby通訊站測量了4個(gè)不同高度的風(fēng)荷載，并且在Cardington進(jìn)行了觀測，得出了不同高度的風(fēng)速與湍流積分尺度變化的關(guān)系。文獻(xiàn)[3]通過現(xiàn)場實(shí)測方法在1986年對悉尼的Belmore體育場進(jìn)行了實(shí)測，證明了實(shí)測與風(fēng)洞試驗(yàn)的風(fēng)壓系數(shù)平均值和極值較為接近，但是脈動(dòng)風(fēng)壓系數(shù)較小。文獻(xiàn)[4]通過風(fēng)洞實(shí)驗(yàn)于1893年在澳大利亞利用噴氣式飛機(jī)產(chǎn)生的氣流測得了縮小后的房屋模型的風(fēng)荷載分布情況。文獻(xiàn)[5]在1955—1957年通過加長風(fēng)洞來流試驗(yàn)段的長度成功模擬出了大氣邊界層。以上研究都是利用現(xiàn)場實(shí)測和風(fēng)洞試驗(yàn)來解決建筑物的湍流來流問題，本文的中心思想是利用數(shù)值模擬方法對大跨度平屋蓋、大跨度鞍形屋蓋、大跨度球面屋蓋以及大跨度懸挑屋蓋進(jìn)行數(shù)值模擬，主要目的是得出其平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)。數(shù)值模擬技術(shù)的基本思想是：把原來在時(shí)間域以及空間域上連續(xù)的物理量的場用一系列有限個(gè)離散點(diǎn)上的變量值的集合來代替，并通過求解代數(shù)方程組獲得場變量的近似值。國內(nèi)諸多專家學(xué)者都利用此方法完成了一些計(jì)算工作，比如陳善群等[6]通過運(yùn)用標(biāo)準(zhǔn)k-ε模型、重整化數(shù)群k-ε模型(RNGk-ε)和雷諾應(yīng)力模型(RSM)對二維單山包和多山包繞流進(jìn)行了數(shù)值模擬，確定了數(shù)值模擬對于山包數(shù)值模擬的可行性。盧春玲等[7]利用數(shù)值模擬中的大渦模擬方法對長沙機(jī)場擴(kuò)建航站樓屋蓋結(jié)構(gòu)進(jìn)行了計(jì)算，得出了屋蓋表面的風(fēng)壓分布以及最不利風(fēng)向角，并利用均方根誤差公式得出脈動(dòng)風(fēng)荷載的研究方法。本文將在這一基礎(chǔ)上對4種大跨度屋蓋進(jìn)行計(jì)算，本文所運(yùn)用的方法是大渦模擬，這是一種能夠在保證計(jì)算精度的情況下占用計(jì)算資源相對較少的方法。

1 研究方法與邊界條件設(shè)定

本文采用大渦模擬方法對平屋蓋、球面屋蓋、鞍形屋蓋和懸挑屋蓋進(jìn)行計(jì)算，并求得它們的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)。大渦模擬方法包括以下3個(gè)方面：

1.1 濾波器

1) 譜空間低通濾波器

(1)

在濾波空間的各個(gè)方向上用相同的濾波器，又稱為各向同性低通濾波，其數(shù)學(xué)表達(dá)式為

Gl(k)=θ(kc-|k|)

(2)

式中θ表示臺(tái)階函數(shù)，當(dāng)|x|<0時(shí)，θ(x)=0；當(dāng)|x|>0時(shí)，θ(x)=1。用kc=π/l表示截?cái)嗖〝?shù)，其中l(wèi)是相當(dāng)?shù)奈锢砜臻g濾波單位長度。

2) 物理空間的盒式濾波器

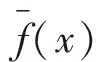
(3)

物理空間的濾波器同樣滿足正則條件，此條件可以保證過濾器內(nèi)各種物理量的守恒性，對于常數(shù)而言在此條件內(nèi)是不變的。

(4)

式中：Ω是過濾的空間體積。1維盒式的濾波器可以表示為

(5)

式中：l是濾波器的單位長度，物理空間盒式濾波器的特點(diǎn)就是以空間長度為標(biāo)準(zhǔn)，當(dāng)脈動(dòng)長度小于濾波器的單位長度時(shí)將會(huì)被過濾掉。

1.2 亞格子尺度模型

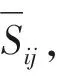
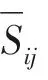
此模型下的速度張量渦黏系數(shù)vt可以如下表示：

(6)

(7)

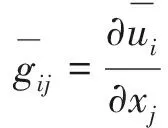
(8)

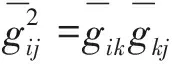
(9)

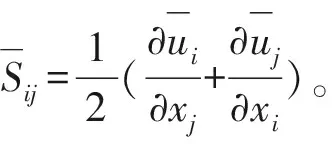
1.3 邊界條件

為了更好地得到入口處的風(fēng)速條件，并準(zhǔn)確模擬入口處風(fēng)的特征，在設(shè)置速度時(shí)采用已編輯好的UDF，使用UDF可以實(shí)現(xiàn)呈現(xiàn)指數(shù)形式的平均風(fēng)剖面：

(10)

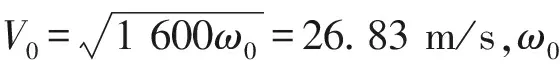
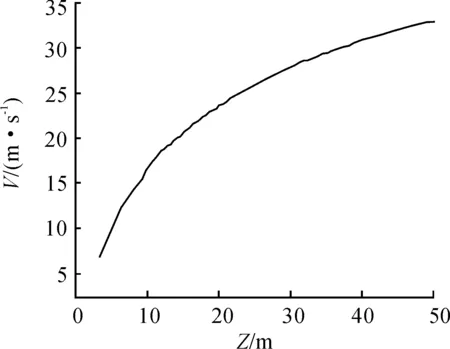
圖1 風(fēng)速剖面

入口處湍流強(qiáng)度邊界條件除了速度外還有兩個(gè)條件需要用UDF進(jìn)行定義與描述， 這兩個(gè)條件分別是湍動(dòng)能k和湍流耗散率ε。湍動(dòng)能k和湍流耗散率ε的數(shù)學(xué)表達(dá)式如下：

k(z)=1.2[I(z)*Vz]2

(11)

(12)

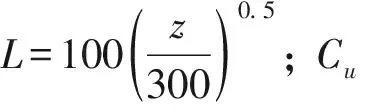
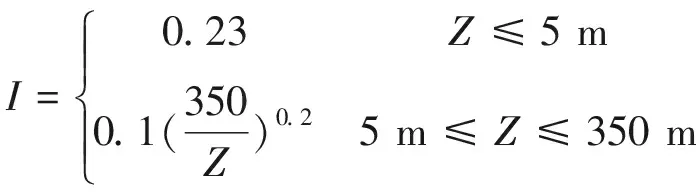
(13)

上表面、下表面和前后壁面條件設(shè)置為固壁無滑移邊界條件(Wall)，左邊界的邊界條件設(shè)置為速度入口(Velocity-inlet)，右邊界的邊界條件設(shè)置為自由出流(Outflow)，方柱表面同樣采用固壁無滑移邊界條件(Wall)。

2 數(shù)值驗(yàn)證

本算例利用ICEM CFD的幾何建模功能生成大跨平屋蓋結(jié)構(gòu)的三維模型，如圖2所示。數(shù)值模型為一個(gè)平屋蓋結(jié)構(gòu)形式，平屋蓋結(jié)構(gòu)被置于一個(gè)矩形的流場中，流場四周封閉。對于所需計(jì)算的平屋蓋結(jié)構(gòu)來說，計(jì)算區(qū)域是一個(gè)足夠大的空間，整個(gè)流場區(qū)域尺寸為80H×10H×15H。其中模型的長為80H、寬為10H、高為15H，模型的原點(diǎn)O定在方柱的左下側(cè)頂點(diǎn)處。計(jì)算模型平屋蓋結(jié)構(gòu)的尺寸的長和寬為600 mm×600 mm，高定義為基本尺寸H=200 mm，因此在數(shù)值模擬中采用與風(fēng)洞試驗(yàn)一致的參數(shù)。

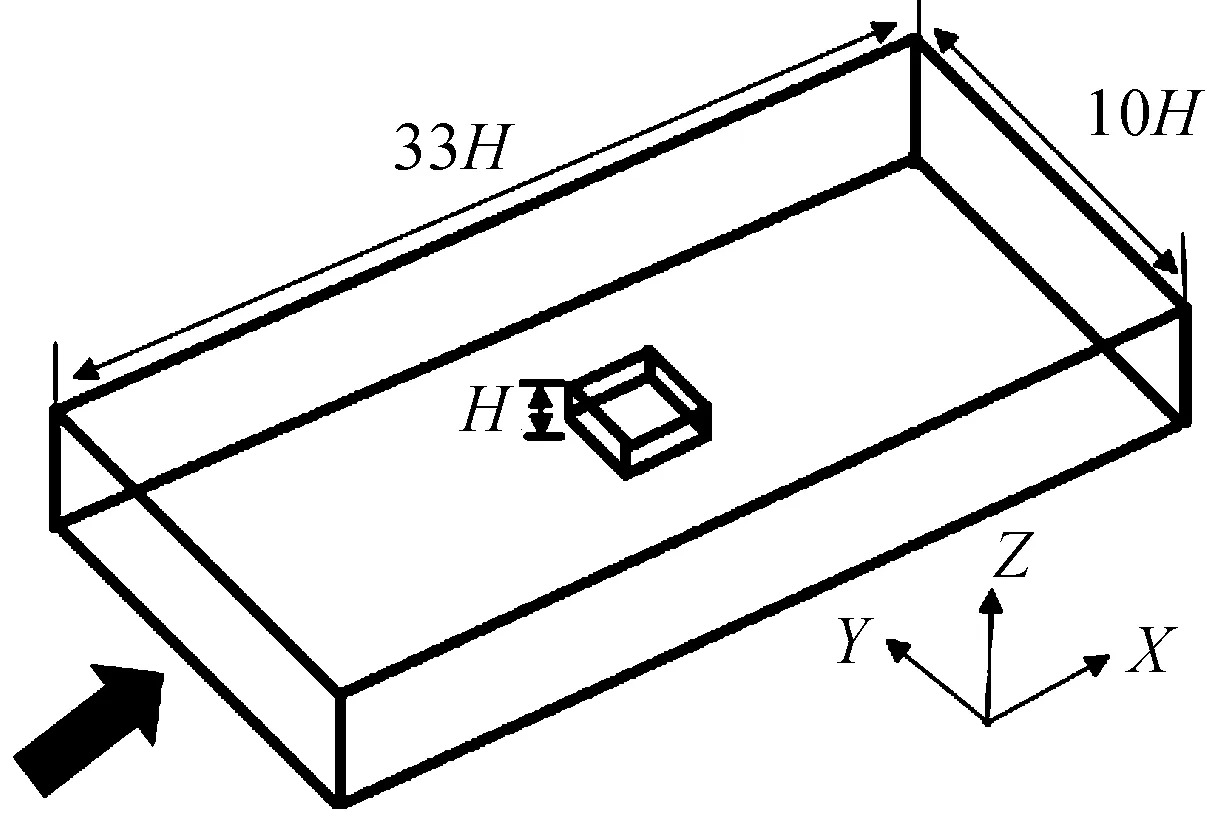
圖2 平屋蓋計(jì)算域

2.1 平均風(fēng)壓系數(shù)驗(yàn)證

針對大跨度平屋蓋選取一系列的觀測點(diǎn)，大跨度平屋蓋的上表面是受風(fēng)力影響最重要的部分，將平屋蓋面上沿著半個(gè)屋面的輪廓路徑a→b→c→d→a按照每段之間取10個(gè)點(diǎn)來研究其平均風(fēng)壓系數(shù)，如圖3所示。由于本算例需證明大渦模型(LES)的計(jì)算精確度，所以不僅提取了該模型下的數(shù)據(jù)點(diǎn)，同樣也提取了利用k-ε模型計(jì)算的數(shù)據(jù)點(diǎn)用以對比。利用前面兩種計(jì)算模型提取平均風(fēng)壓系數(shù)測點(diǎn)上的數(shù)據(jù)之后，與試驗(yàn)數(shù)據(jù)[8]進(jìn)行對比，結(jié)果如圖4所示。結(jié)果顯示，大渦模擬(LES)較實(shí)驗(yàn)數(shù)據(jù)相接近，而k-ε模型的數(shù)據(jù)所展現(xiàn)的趨勢較實(shí)驗(yàn)數(shù)據(jù)相差較大。相比較之下，大渦模擬(LES)的數(shù)據(jù)結(jié)果較好，平均風(fēng)壓系數(shù)的風(fēng)洞試驗(yàn)結(jié)果和數(shù)值模擬結(jié)果如圖5、6所示。

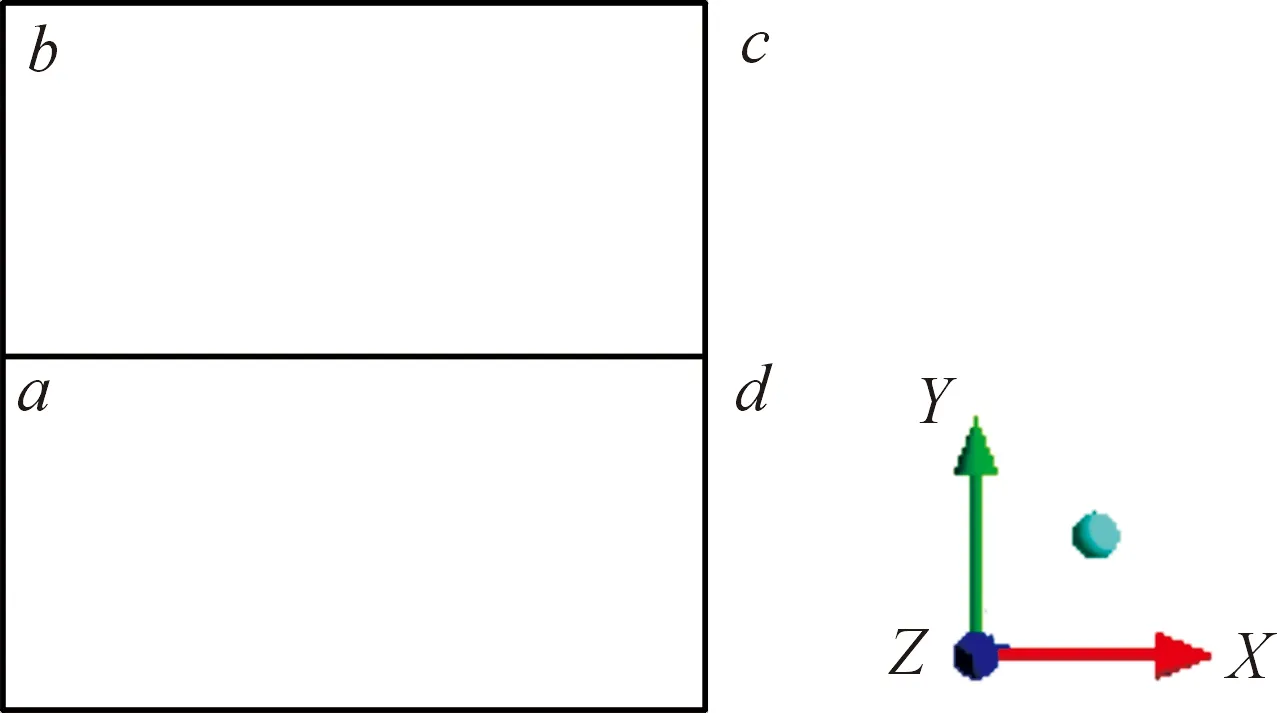
圖3 觀測點(diǎn)的選取

圖4 數(shù)據(jù)對比

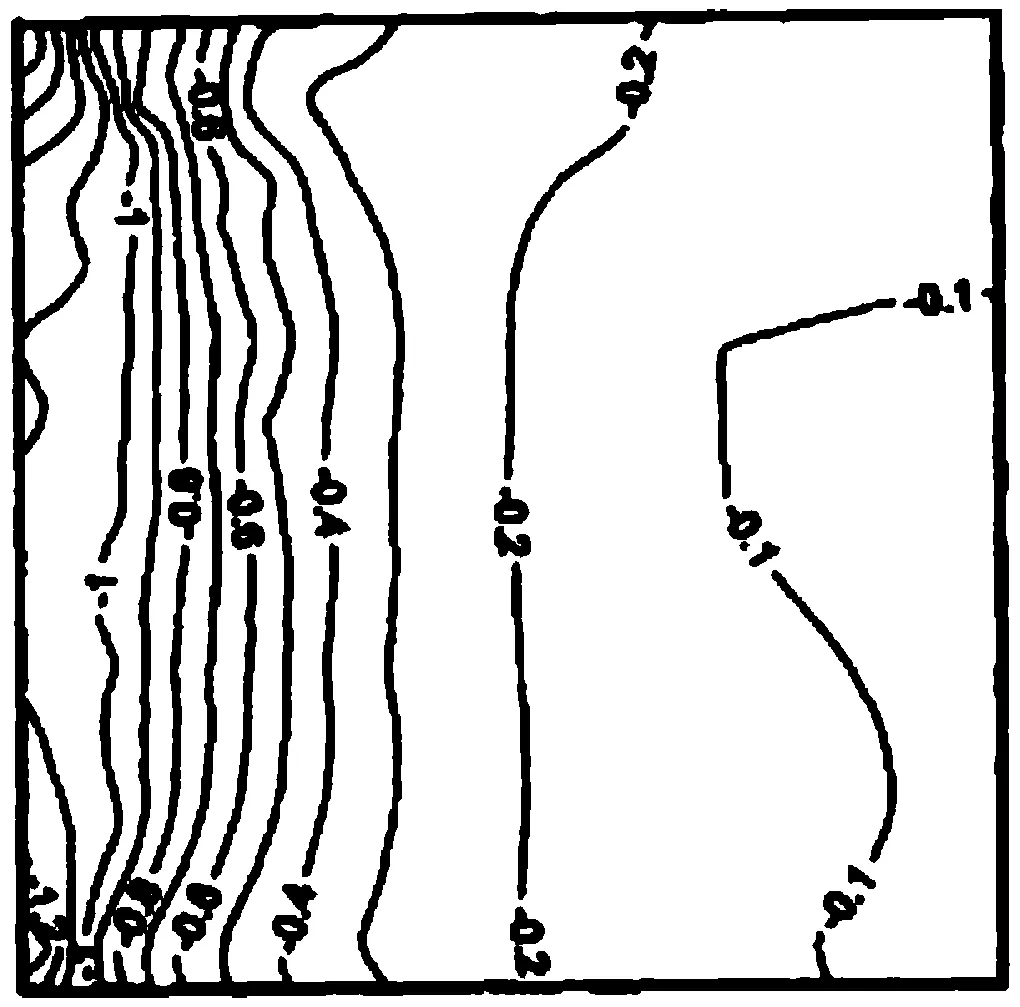
圖5 風(fēng)洞試驗(yàn)結(jié)果

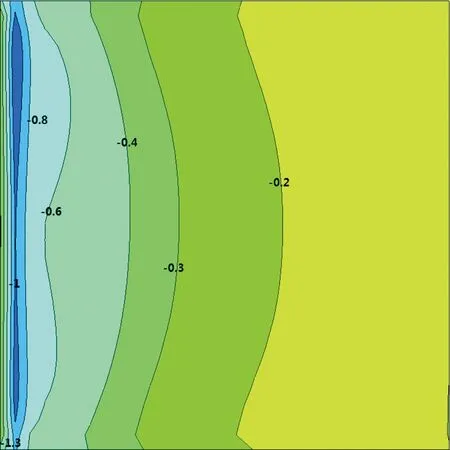
圖6 數(shù)值模擬結(jié)果

2.2 脈動(dòng)風(fēng)壓系數(shù)驗(yàn)證

利用LES計(jì)算得出的脈動(dòng)風(fēng)壓系數(shù)與試驗(yàn)結(jié)果的對比如圖7所示。與平均風(fēng)壓系數(shù)的取法一樣，沿著半個(gè)屋面的輪廓a→b→c→d→a提取脈動(dòng)系數(shù)的值，作圖與試驗(yàn)數(shù)據(jù)進(jìn)行比較，如圖8所示。

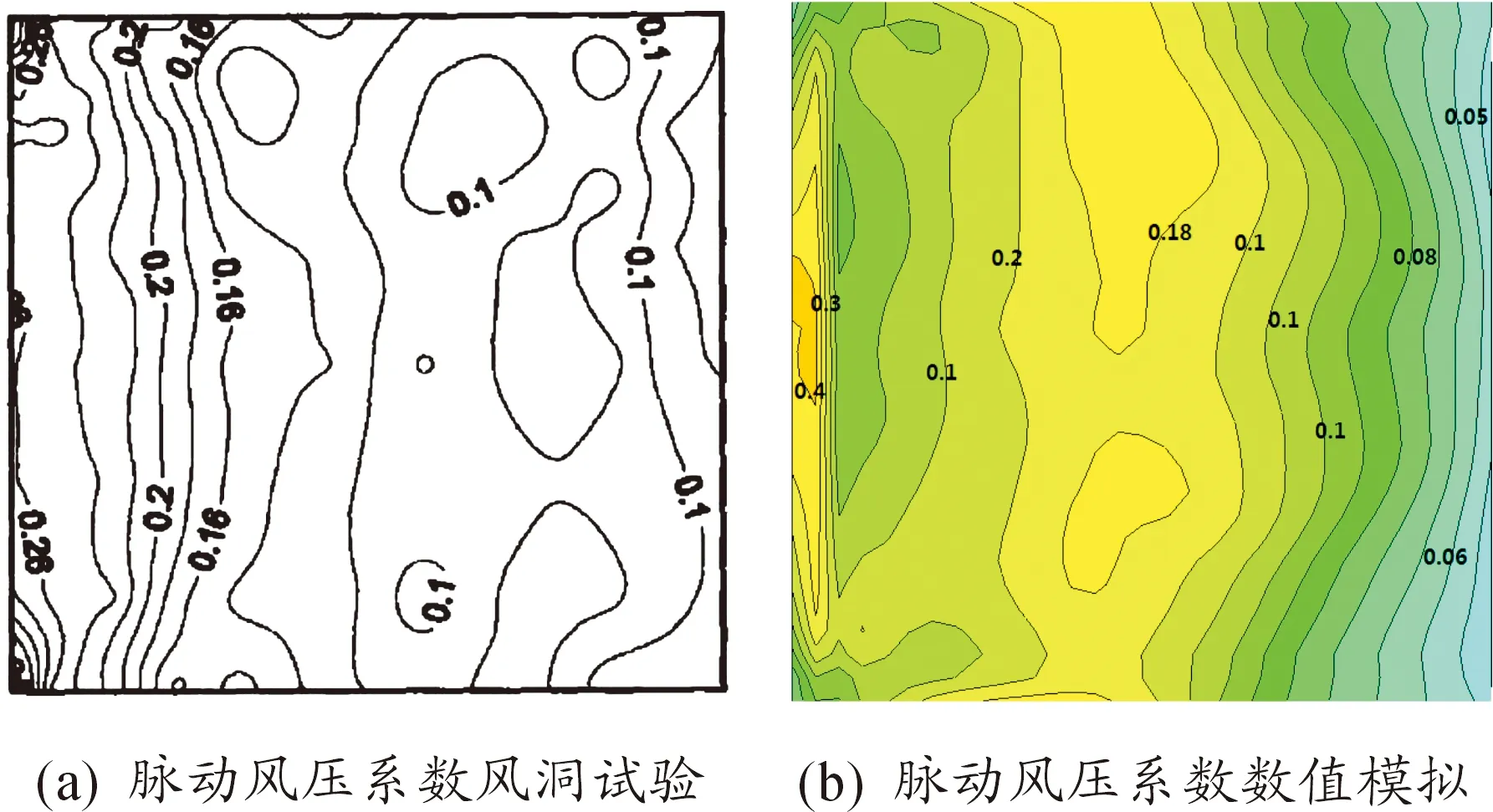
圖7 LES法與風(fēng)洞試驗(yàn)對比

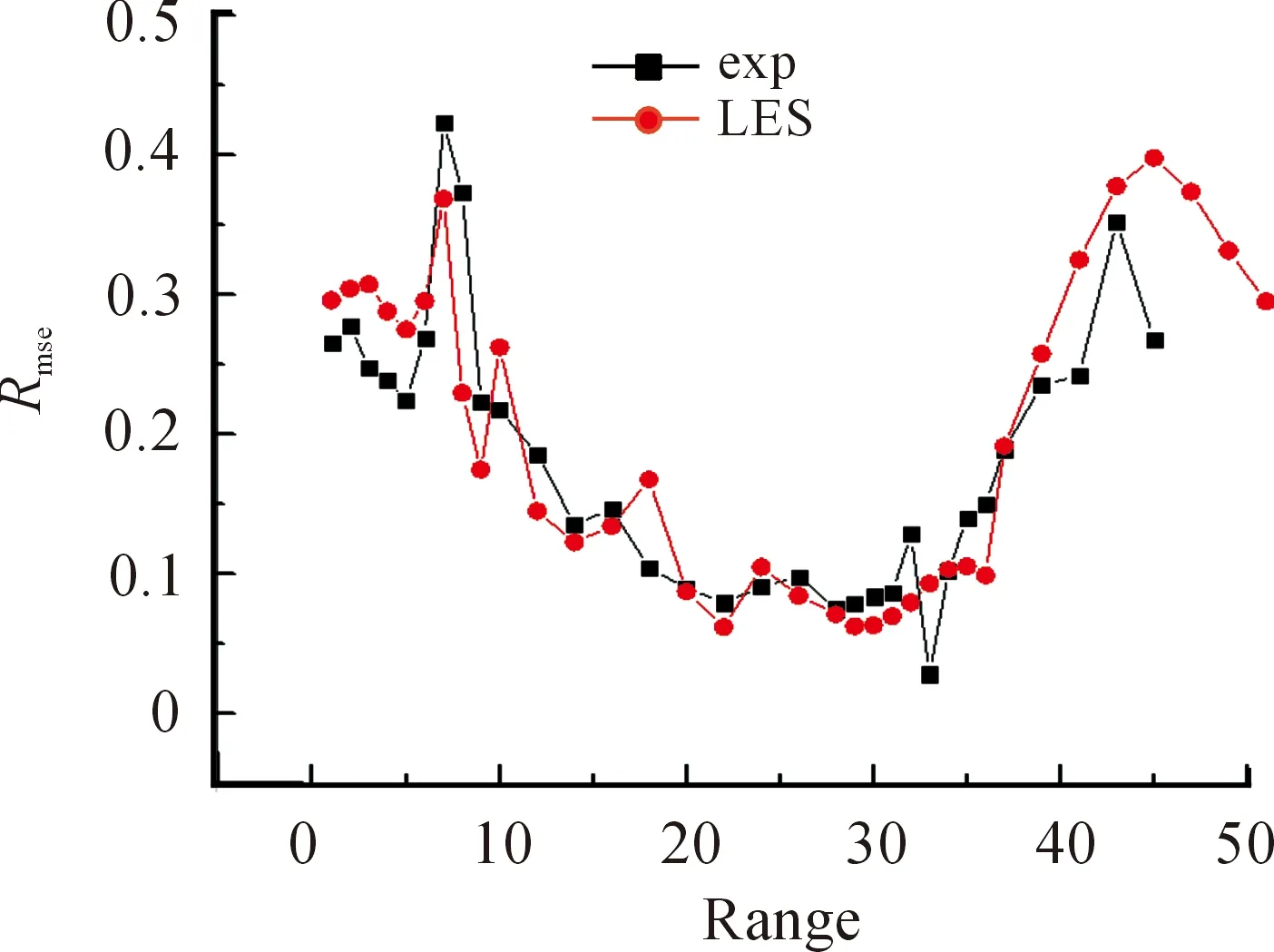
圖8 觀測點(diǎn)數(shù)據(jù)對比

通過對結(jié)果的分析，可以得出如下說明：

1) 脈動(dòng)風(fēng)壓系數(shù)表達(dá)式為

(14)

均方根誤差表達(dá)式為

(15)

通過上式可以看出：脈動(dòng)風(fēng)壓系數(shù)的表達(dá)式與均方根誤差的表達(dá)式是一樣的，均方根誤差是觀測值與真值偏差的平方和觀測次數(shù)n比值的平方根，均方根誤差可以很好地反映測量的精度。同理，脈動(dòng)風(fēng)壓系數(shù)也是觀測點(diǎn)風(fēng)壓和平均風(fēng)壓的差求均方根，所以可以得出一個(gè)結(jié)論：脈動(dòng)風(fēng)壓系數(shù)與試驗(yàn)對比的準(zhǔn)確度反映了所求風(fēng)場的精度。

2) 利用LES計(jì)算得出的結(jié)果與風(fēng)洞試驗(yàn)結(jié)果相比存在誤差，但是最大誤差相差在10%以內(nèi)。根據(jù)平均風(fēng)壓系數(shù)Cp和脈動(dòng)風(fēng)壓系數(shù)RMSE數(shù)據(jù)與風(fēng)洞試驗(yàn)數(shù)據(jù)對比，發(fā)現(xiàn)兩者的基本發(fā)展趨勢是一樣的，數(shù)值存在誤差，但誤差不大，因此利用LES方法對建筑物在大氣邊界層中湍流進(jìn)行數(shù)值模擬是可行的。

3 大跨度屋蓋結(jié)構(gòu)的LES數(shù)值模擬

3.1 球面屋蓋

杭州國際會(huì)議中心以舉辦大型國際會(huì)議和白金五星級酒店為標(biāo)準(zhǔn)進(jìn)行功能設(shè)計(jì)，其采用鋼結(jié)構(gòu)建設(shè)，建筑整體高度為85 m，主體由13 m高橢圓形裙房和直徑85 m球體組成。如圖9所示，杭州國際會(huì)議中心是一個(gè)大跨度球面屋蓋結(jié)構(gòu)，球體部分可以簡化為如圖9右圖所示的模型，其中OA=OC=50 m、DA=DB=40 m、OD=30 m。整個(gè)模型的計(jì)算域?yàn)? 220 m×920 m×340 m，將球體迎風(fēng)面與左側(cè)面交點(diǎn)投影在底面設(shè)為0點(diǎn)，如圖10所示，從速度入口到建筑本體迎風(fēng)面切平面的距離為400 m。

圖9 杭州國際會(huì)議中心

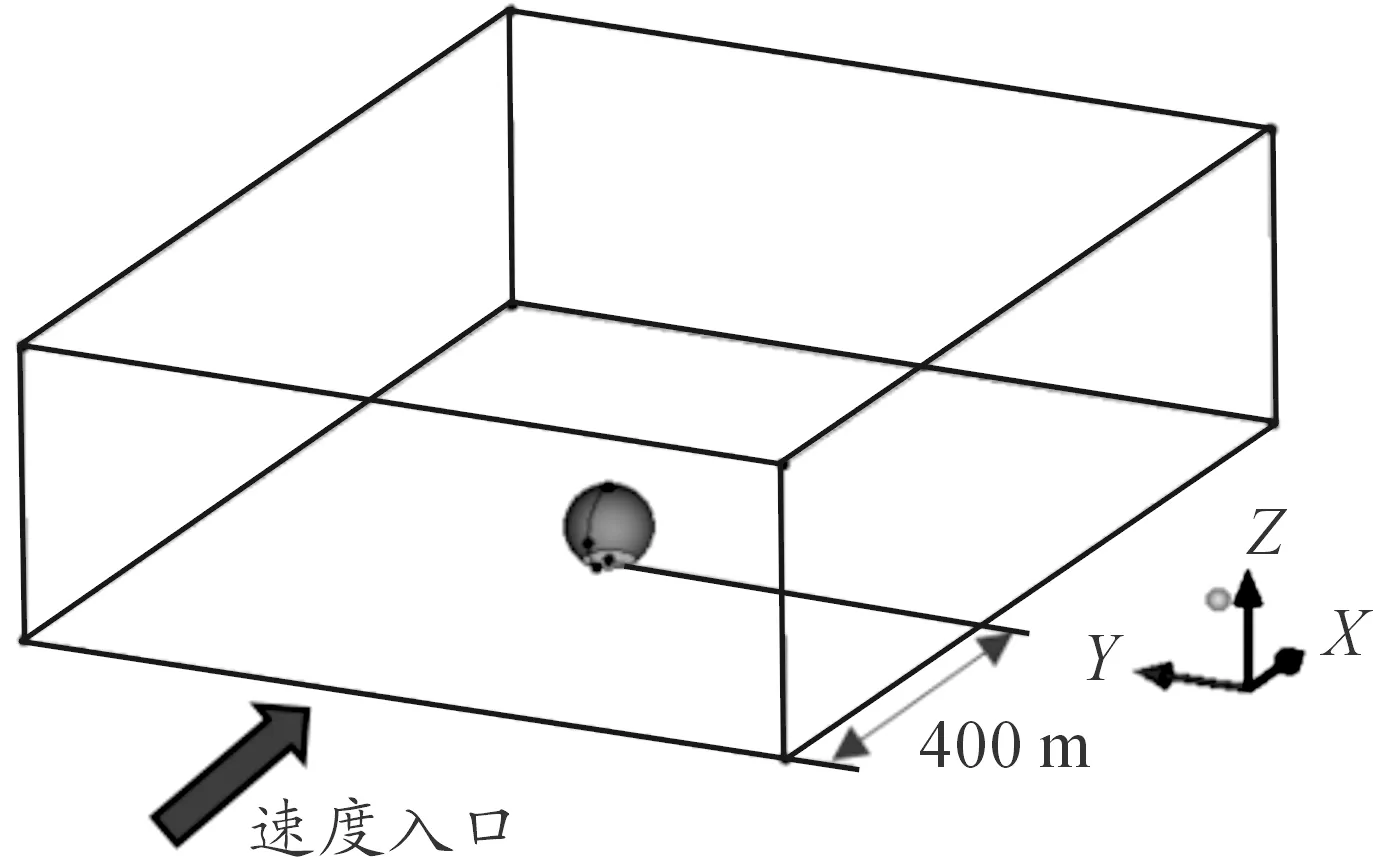
圖10 計(jì)算域示意圖

3.2 球面屋蓋的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)

得到計(jì)算結(jié)果后，在杭州國際會(huì)議中心模型表面取X=0 m和Y=0 m這兩條線，如圖11所示，并且在這兩條線上各取22個(gè)點(diǎn)。由于國家規(guī)范并沒有規(guī)定球面屋蓋體型系數(shù)參考點(diǎn)的選定，本算例取球體頂點(diǎn)為參考點(diǎn)，球體頂點(diǎn)坐標(biāo)為(110,110,85)，分別對這兩條線上的點(diǎn)求量綱為1值，保留小數(shù)點(diǎn)后3位，取得點(diǎn)上的平均風(fēng)壓系數(shù)，如圖12所示。根據(jù)脈動(dòng)風(fēng)壓系數(shù)公式(14)(15)取得測點(diǎn)上的脈動(dòng)風(fēng)壓系數(shù)，如圖13所示。

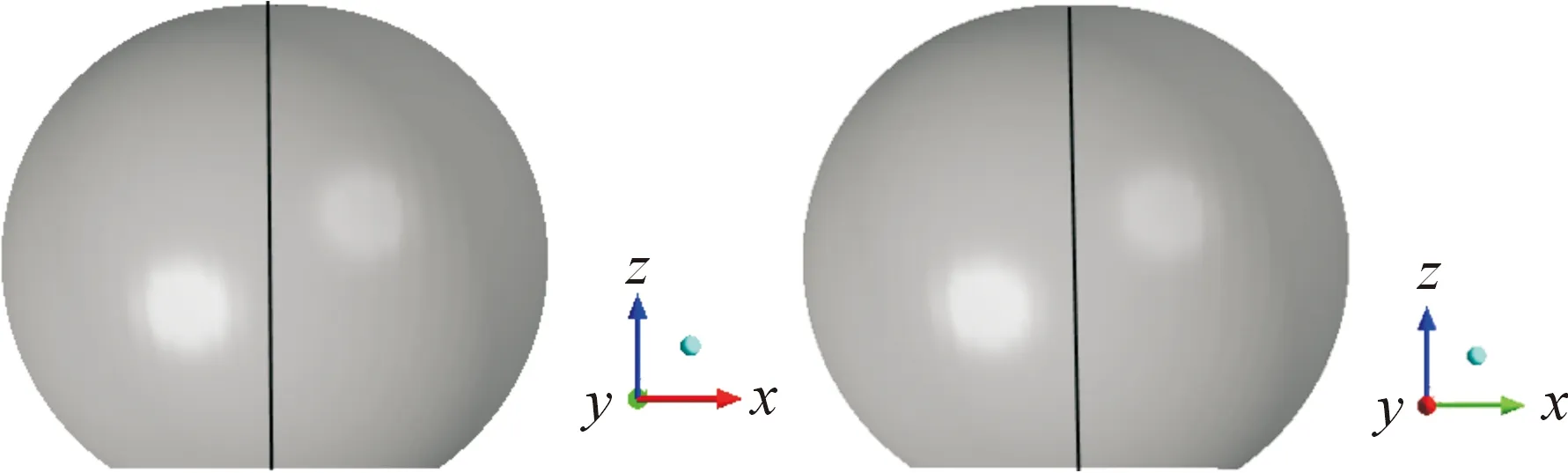
圖11 杭州國際會(huì)議中心風(fēng)壓系數(shù)選取線

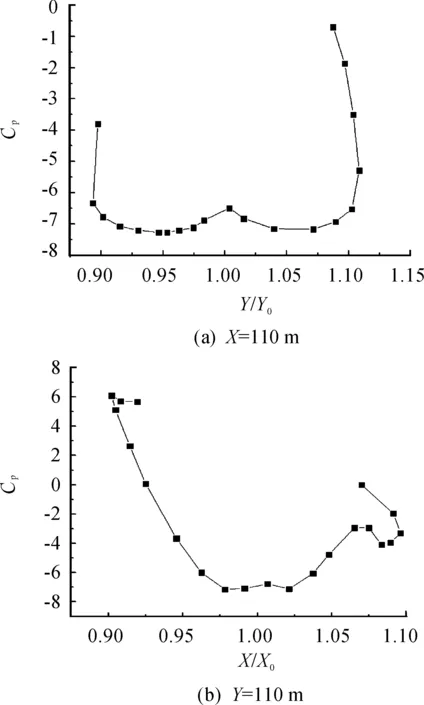
圖12 杭州國際會(huì)議中心平均風(fēng)壓系數(shù)

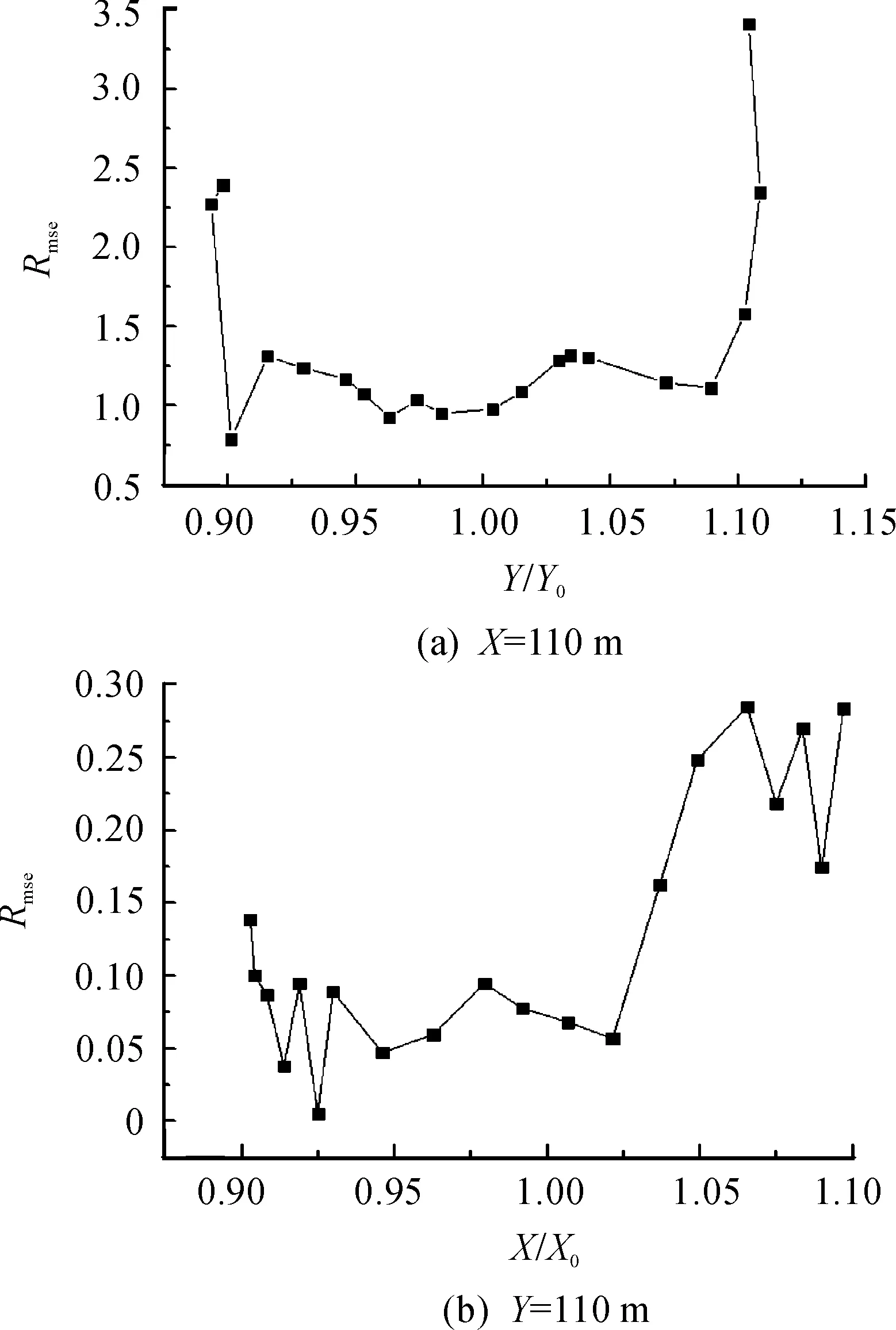
圖13 杭州國際會(huì)議中心脈動(dòng)風(fēng)壓系數(shù)

3.3 鞍形屋蓋

大跨度鞍形屋蓋不僅具有類似方柱繞流的流動(dòng)特性，還具有特殊的負(fù)高斯曲率弧形屋面的形狀特性。模型參考文獻(xiàn)[9]，使用前處理軟件ICEM對0°、45°和90°這3個(gè)風(fēng)向角下的大跨度鞍形屋蓋進(jìn)行建模和網(wǎng)格劃分，整個(gè)模型的計(jì)算域?yàn)?.35 m×4.25 m×1.2 m，從速度入口到鞍形屋蓋的距離為3.4 m，其整體流域如圖14所示。

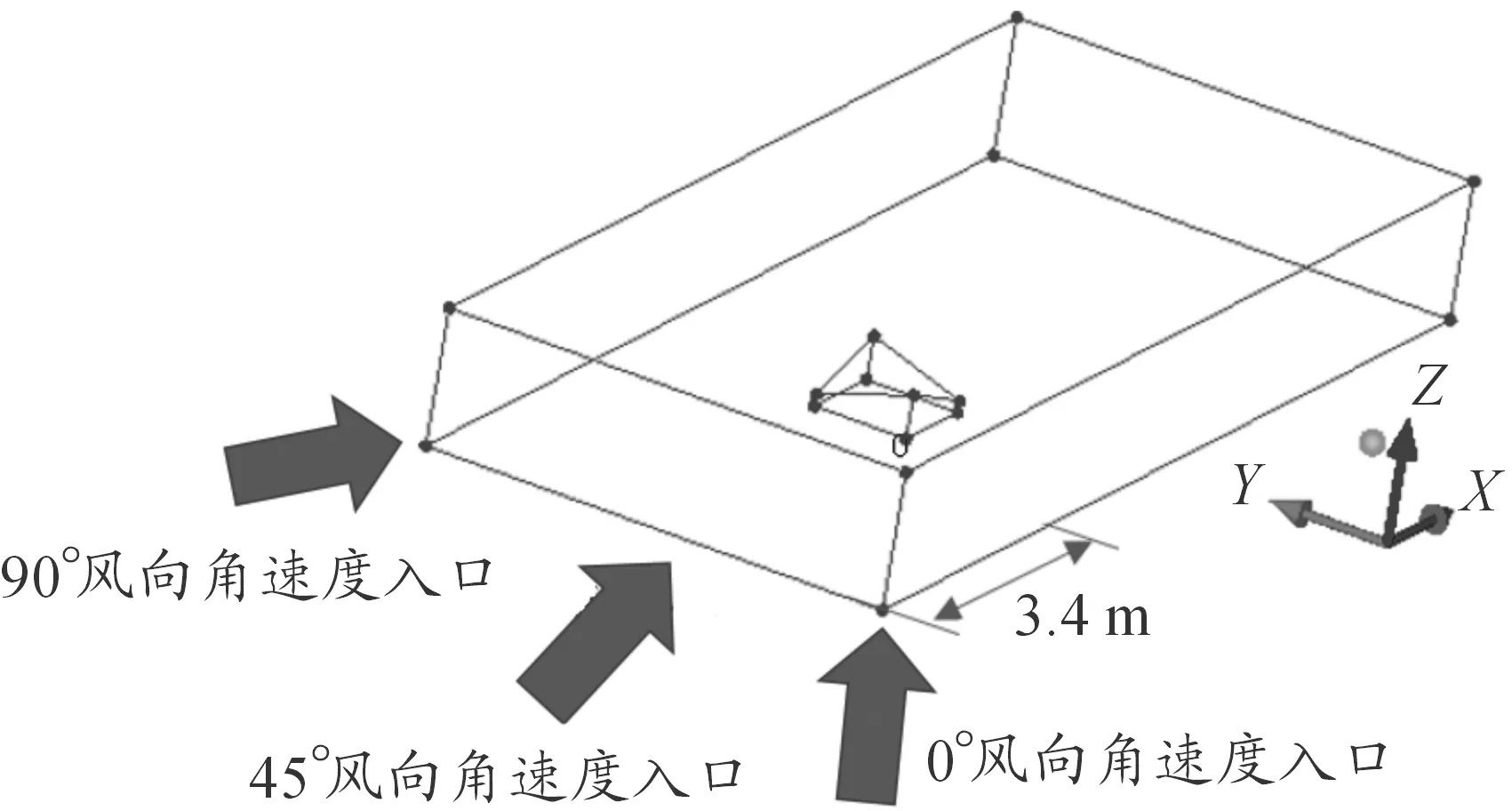
圖14 鞍形屋蓋整體流域

3.4 3個(gè)風(fēng)向角下大跨度鞍形屋蓋的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)

對計(jì)算結(jié)果進(jìn)行處理，在鞍形屋蓋表面各取2條交于中點(diǎn)的線段，對于0°的鞍形屋蓋取迎風(fēng)處最高的頂點(diǎn)為參考點(diǎn)O點(diǎn)，參考點(diǎn)坐標(biāo)為(3.4,2.125,0.38)；對于45°的鞍形屋蓋取迎風(fēng)面下側(cè)最高點(diǎn)為參考點(diǎn)O1點(diǎn)，參考點(diǎn)坐標(biāo)為(3.4,1.7,0.38)；對于90°的鞍形屋蓋取迎風(fēng)處的最低點(diǎn)為參考點(diǎn)O2點(diǎn)，參考點(diǎn)坐標(biāo)為(3.4,2.125,0.1)，如圖15所示。在每條線上取10個(gè)點(diǎn)并且求它們的無量綱值，保留小數(shù)點(diǎn)后3位，取得每個(gè)點(diǎn)上的平均風(fēng)壓系數(shù)，如圖16所示。再根據(jù)脈動(dòng)風(fēng)壓系數(shù)公式(14)(15)求得每個(gè)點(diǎn)上的脈動(dòng)風(fēng)壓系數(shù)，如圖17所示。

圖15 鞍形屋蓋參考點(diǎn)和數(shù)據(jù)提取線的選取

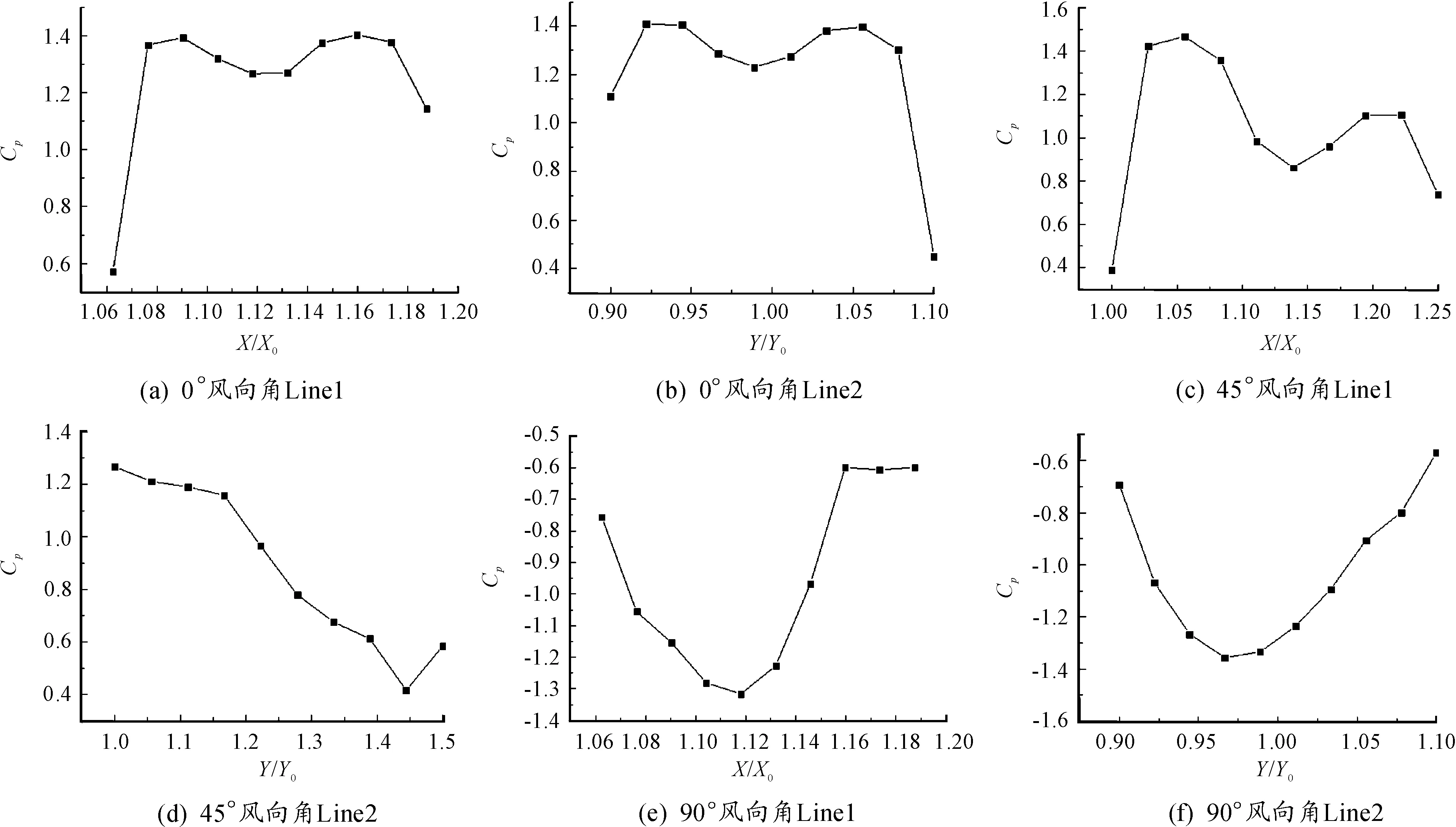
圖16 3個(gè)風(fēng)向角下的平均風(fēng)壓系數(shù)

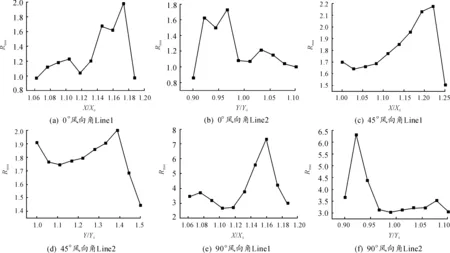
圖17 3個(gè)風(fēng)向角下的脈動(dòng)風(fēng)壓系數(shù)

3.5 懸挑屋蓋

在目前諸多的大跨度空間結(jié)構(gòu)中，懸挑結(jié)構(gòu)造型獨(dú)特且具有遮陽避雨的功能，屬于典型的風(fēng)敏感結(jié)構(gòu)，而風(fēng)荷載是懸挑結(jié)構(gòu)的控制荷載之一。本文的大跨度懸挑屋蓋形式與文獻(xiàn)[10-12]中試驗(yàn)的幾何形式保持一致，將看臺(tái)簡化成一個(gè)梯形，如圖18(a)所示，整個(gè)模型采用縮尺比例，具體尺寸為：從地面到屋蓋頂部H=0.25 m，從地面到看臺(tái)的距離H1=0.2 m，從看臺(tái)頂部到屋蓋頂部的距離H2=0.05 m，看臺(tái)頂部d=0.02 m，看臺(tái)底部的寬度D=0.22 m。也就是說，簡化的三角形看臺(tái)的傾角度數(shù)α=45°，屋蓋寬度D=0.25 m，屋蓋厚度h=0.01 m，整個(gè)屋蓋和看臺(tái)的長度取相同值L=L1=1 m，屋蓋傾角取0°。對于閉口式的懸挑屋蓋，在看臺(tái)和屋蓋之間還有厚度為0.02 m的1個(gè)隔墻，2種模型剖面圖見圖18(b)和18(c)。為了使計(jì)算結(jié)果更準(zhǔn)確以及避免四周邊界對流場的影響，2個(gè)模型的計(jì)算域均取10 m×4.5 m×1.6 m。為了使來流充分發(fā)展，氣流入口處距離模型迎風(fēng)面1.25 m，來流風(fēng)向沿x軸方向并且與結(jié)構(gòu)側(cè)面保持平行，見圖19。目前對于懸挑屋蓋網(wǎng)格的劃分一般是以非結(jié)構(gòu)性網(wǎng)格為主，也有混合型網(wǎng)格。通過前面的介紹已經(jīng)知道了結(jié)構(gòu)性網(wǎng)格的計(jì)算精度要高于其他形式的網(wǎng)格，所以本節(jié)懸挑模型同樣采用結(jié)構(gòu)性網(wǎng)格劃分。本算例采用了“Y”型剖分使結(jié)構(gòu)性網(wǎng)格更貼合懸挑的表面，網(wǎng)格劃分完成之后懸挑結(jié)構(gòu)表面的網(wǎng)格如圖20所示。

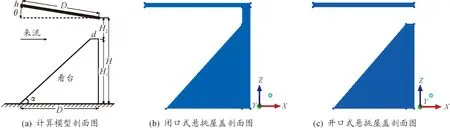
圖18 計(jì)算模型的剖面圖

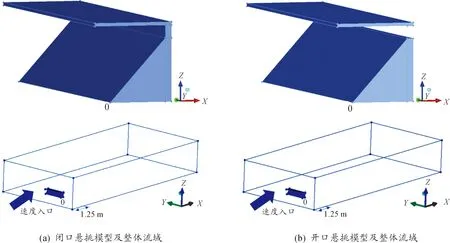
圖19 2種懸挑模型及相應(yīng)的計(jì)算域

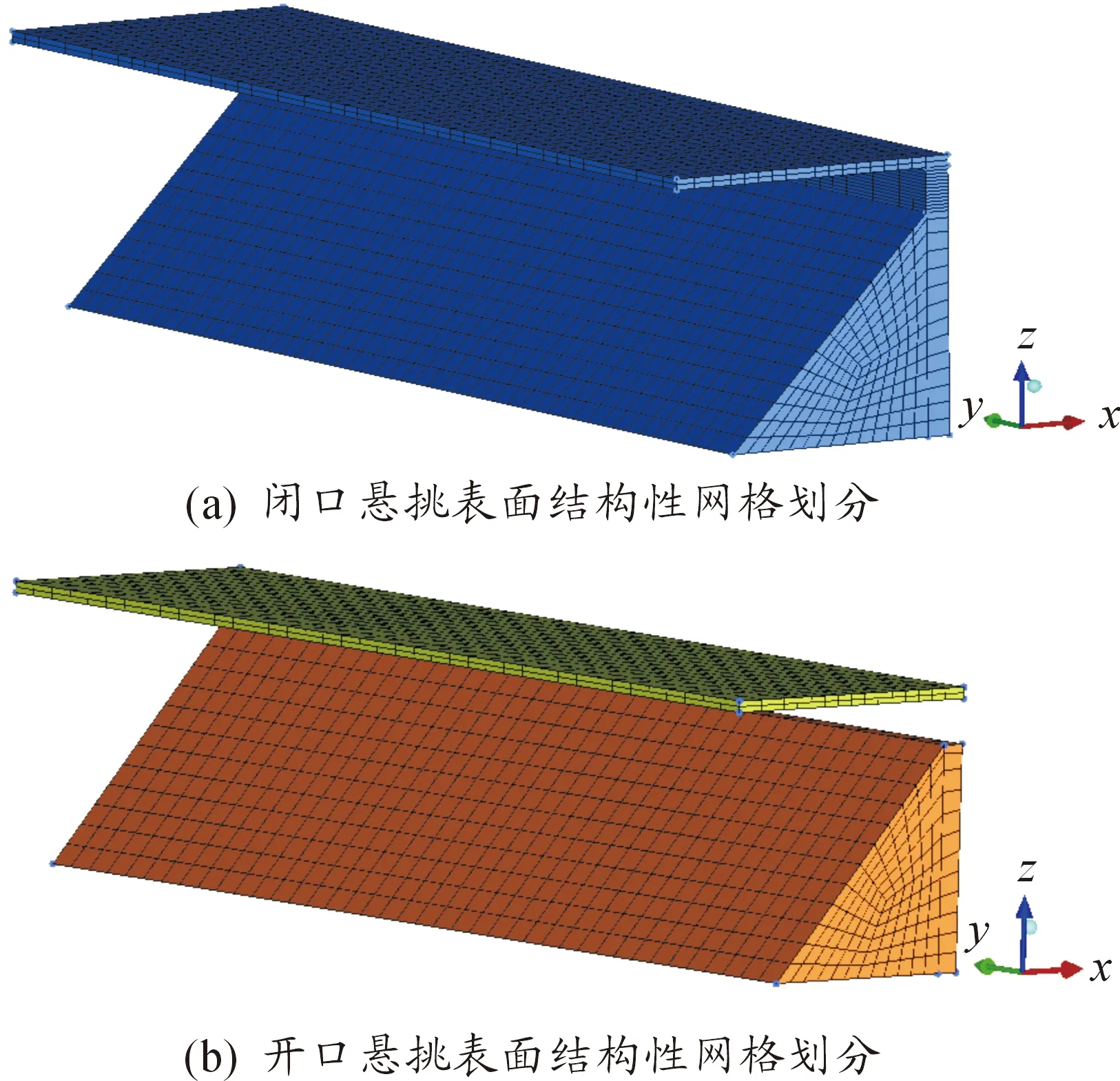
圖20 2種懸挑結(jié)構(gòu)表面結(jié)構(gòu)性網(wǎng)格劃分

3.6 2種形式大跨度懸挑結(jié)構(gòu)的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)

得到計(jì)算結(jié)果之后，先在懸挑結(jié)構(gòu)表面選取1個(gè)參考點(diǎn)，然后再選取2條參考線，并在每條線上提取10個(gè)數(shù)據(jù)點(diǎn)，通過計(jì)算最后可得平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)的分布。其中，參考點(diǎn)選取屋蓋迎風(fēng)面最左下角的點(diǎn)，坐標(biāo)為(1.2,1.75,0.25)。取屋蓋表面對稱于X軸和Y軸的兩條線Line1和Line2,如圖21所示，并在這兩條線上各取10個(gè)數(shù)據(jù)點(diǎn)，取其無量綱值，保留小數(shù)點(diǎn)后3位，根據(jù)公式求得每條線上的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)，如圖22～25所示。

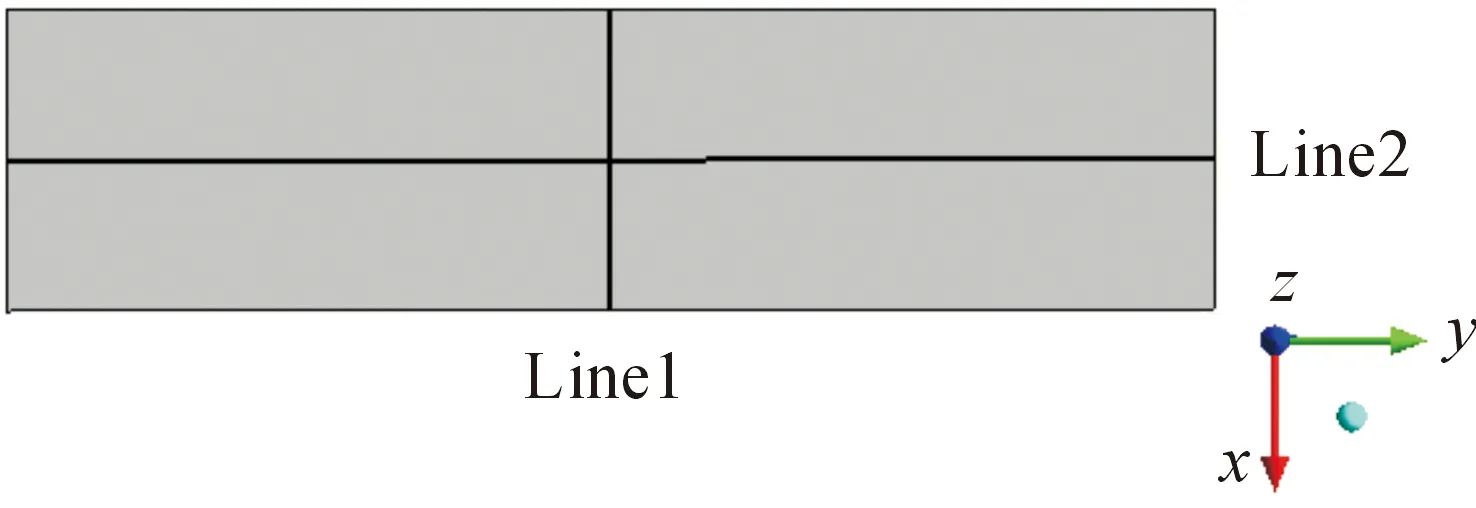
圖21 懸挑結(jié)構(gòu)參考點(diǎn)和數(shù)據(jù)提取線的選取

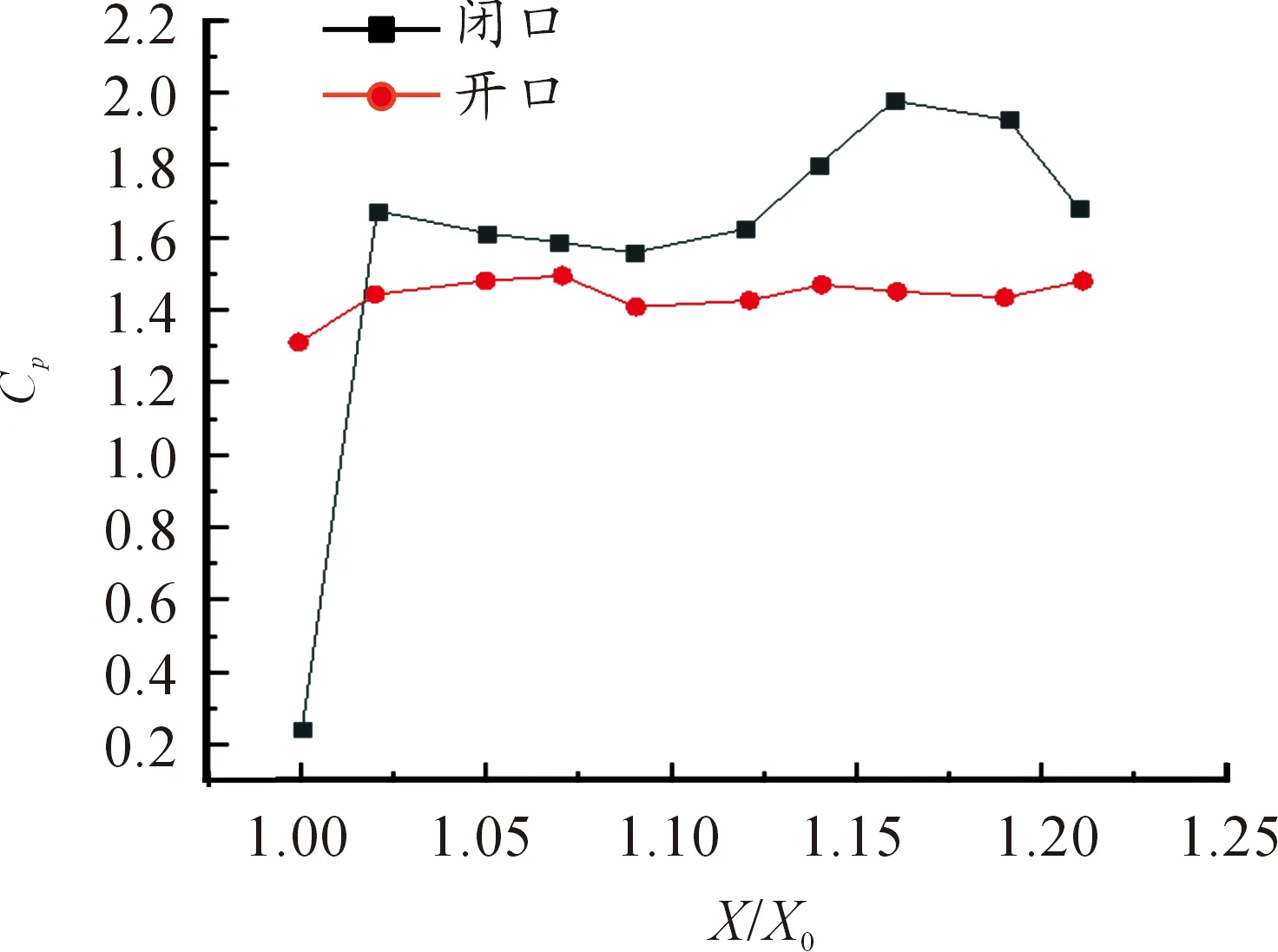
圖22 2種懸挑結(jié)構(gòu)Line1處的平均風(fēng)壓系數(shù)

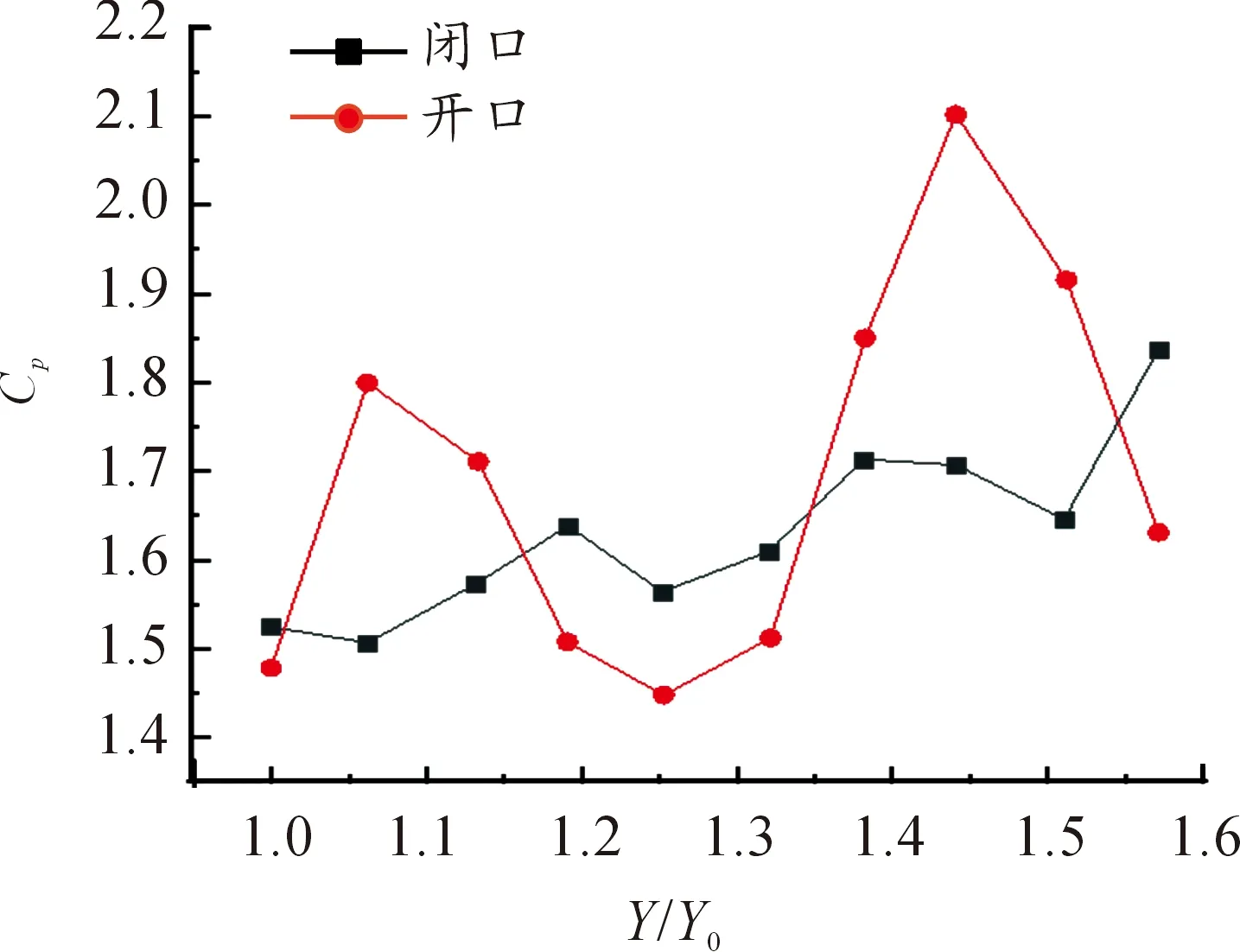
圖23 2種懸挑結(jié)構(gòu)Line2處的平均風(fēng)壓系數(shù)

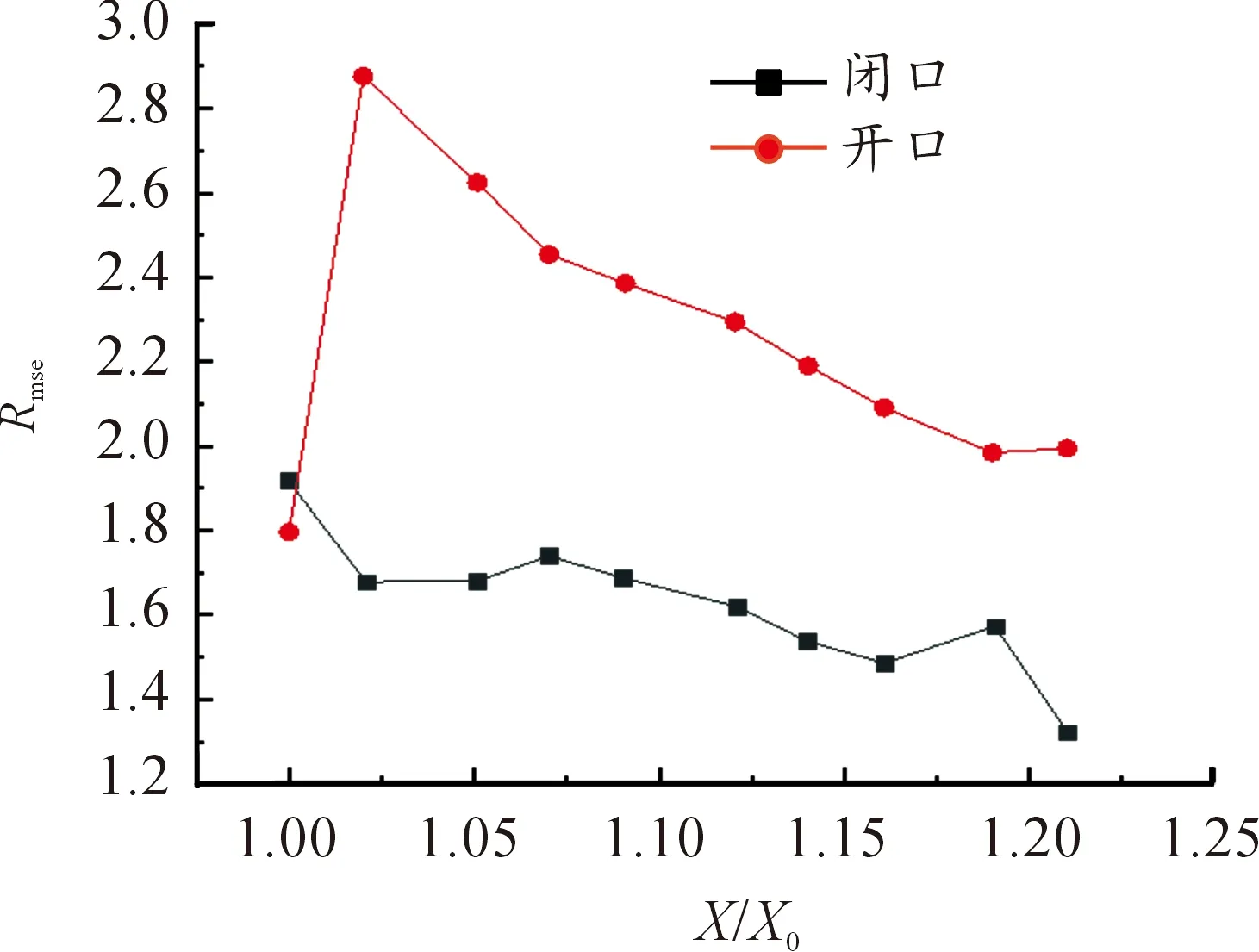
圖24 2種懸挑結(jié)構(gòu)Line1處的脈動(dòng)風(fēng)壓系數(shù)

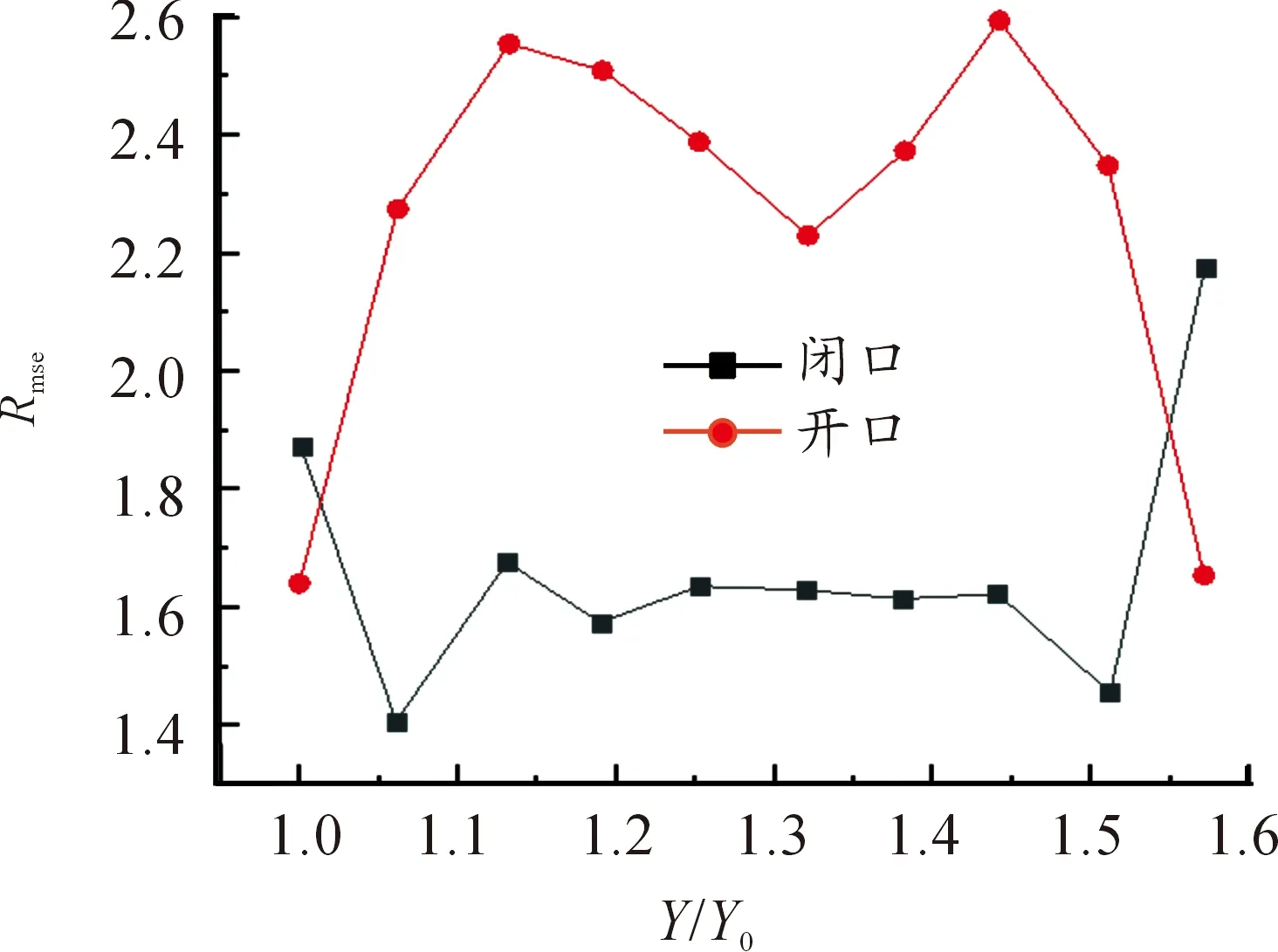
圖25 2種懸挑結(jié)構(gòu)Line2處的脈動(dòng)風(fēng)壓系數(shù)

4 結(jié)論

通過對4種大跨度屋蓋結(jié)構(gòu)的大渦模擬計(jì)算，可以得出如下結(jié)論：

1) 首先通過對大跨度平屋蓋的計(jì)算，并對比與設(shè)置條件相同的實(shí)驗(yàn)結(jié)果，發(fā)現(xiàn)通過大渦模擬可以得出較準(zhǔn)確的結(jié)果。

2) 球面屋蓋計(jì)算模型采用等比例簡化過的杭州國際會(huì)議中心模型。通過觀察可得，與X=110 m處的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)相比，Y=110 m處較為穩(wěn)定，特別是Y=110 m處的脈動(dòng)風(fēng)壓系數(shù)振蕩幅度較大；鞍形屋蓋的計(jì)算采用矢跨比為1/6的模型，對0°、45°和90°這3個(gè)不同風(fēng)向角的計(jì)算，通過平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)可知45°時(shí)的振蕩最小，對鞍形屋蓋的現(xiàn)場布置時(shí)需要考慮風(fēng)向角的影響；對懸挑屋蓋的計(jì)算采用最不利風(fēng)向角位置(0°風(fēng)向角)，設(shè)置懸挑形式為閉口和開口兩種。相比之下懸挑頂部垂直于來流方向區(qū)域的平均風(fēng)壓系數(shù)和脈動(dòng)風(fēng)壓系數(shù)振蕩較大，出于安全考慮在建設(shè)時(shí)需要加固。