山區大跨度變截面鋼箱梁橋靜力特性分析

沈明軒　杜斌　郭仔翔　張玉濤　車小林　張興

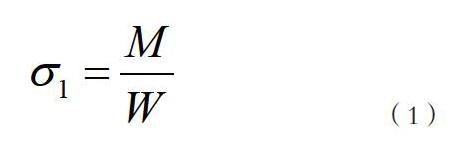
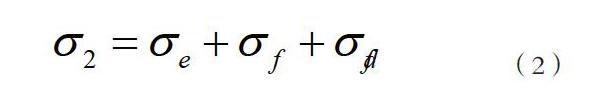
摘 要：以山區某大跨度變截面鋼箱連續梁橋為依托，使用有限元軟件Midas Civil建立空間有限元模型進行計算分析，揭示各種荷載工況下變截面連續鋼箱梁橋的受力特性和線形變化規律。研究結果表明：對于大跨度變截面連續鋼箱梁而言，恒載對主梁的線形和應力影響最大。在寒冷地區（升/降溫為460C/-210C），溫度對主梁應力和線形的影響較小。

關鍵詞：變截面;大跨度連續梁橋;靜力分析;受力特性;線形變化

中圖分類號：U44? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? 文章編號：1006—7973（2019）10-0111-03

鋼材是一種抗拉、抗壓、抗剪強度較高的均質材料[1][2]，因此鋼橋具備結構自重輕、跨越能力大、工業制作程度高、運輸方便、施工速度快等特點，逐漸成為山區新建橋梁的一種重要選擇。鋼箱梁橋是由正交異性橋面板和帶肋薄鋼板制成的底板、腹板和翼緣板構成[3][4]。相較于混凝土箱梁，鋼箱梁的頂板、腹板和底板比較薄，具有良好的抗彎、抗剪能力。但抗扭能力差，通常需要設置相應數量的橫隔板來提高橋梁的整體剛度，以改善連續鋼箱梁抵抗扭轉、畸變的性能。

當前中外眾多專家學者針對不同結構形式，相繼提出了各種各樣的計算理論和分析方法，大致分為解析法，半解析法，數值法三類[5]～[8]。單梁法是一種常用數值模擬方法，該方法基于系梁理論進行計算，通常把連續梁橋當作集中在橋梁軸線中心處的單梁來計算[9]。

本文以貴州某大跨度連續鋼箱梁為例，利用有限元軟件MIDAS/Civil建立變截面鋼箱梁有限元模型，使用單梁法對結構進行靜力特性計算[10]，分析橋梁在各種荷載工況作用下的應力響應和線性變化。

1 工程概況及模型建立

該工程為四跨連續梁橋，跨徑組合為39m+71m+39m+39m，橋梁全長為188m，前三跨主梁采用變截面連續鋼箱梁結構體系，梁高從2.0m漸變至3.5m，第四跨主梁為等截面鋼箱梁，梁高為2.0m，縱向設置單向0.9%的縱坡，縱坡由0#臺至4#臺方向。橋寬16.5m，布置兩車道，橋面橫向設置單向1.5%橫坡。連續鋼箱梁采用單箱四室的箱形截面形式，頂板采用帶U肋的正交異性鋼橋面板，腹板和底板為帶I形肋的薄鋼板，在縱橋向每隔2.5m設置一道橫隔板。本文采用大型橋梁專業軟件MIDAS Civil建立連續鋼箱梁的空間桿系有限元模型，利用梁單元來模擬由橋面板、底板、腹板、縱向加勁肋和橫隔板及翼緣板構成的橋梁上部結構。并考慮以下幾種荷載工況進行靜力特性計算，分別為：自重作用、二期恒載作用、溫度作用、車道作用，全橋上部主體結構共劃分為98個節點，節點號為1～98;全橋劃分為97個單元，單元劃分為1～97，上部結構計算模型如圖1所示。在節點1、節點20、節點50、節點80及節點98采用一般約束分別模擬橋臺和橋墩支座約束。

2 主體結構應力分析

鋼箱梁屬于薄壁金屬箱體結構，在進行應力分析時，假設鋼箱梁為彈塑性體[13]。對于大跨度鋼箱梁橋，恒載占總荷載的比例非常大，進行空間有限元模擬時，縱向對稱撓曲應力對鋼箱梁的影響遠大于偏心荷載作用。恒載作用下，橫截面應力按下式計算：

式中表示縱向對稱撓曲作用下截面應力，M表示縱向對稱撓曲作用產生彎矩，W表示抗彎截面模量。

在偏心荷載作用下，縱橋向彎曲扭轉作用在橫截面上形成縱向正應力和剪應力，橫向彎扭作用在箱梁薄壁桿件間形成橫向彎曲應力和剪應力。偏載作用引起鋼箱梁橫截面應力變化，橫截面應力按下式計算：

式表示偏心荷載作用下截面應力，表示縱向彎曲正應力，表示橫向扭轉正應力，為畸變翹曲正應力。

根據上述分析，并結合相關強烈設計規范對結構應力要求驗算鋼箱梁截面應力。考慮橋自重作用（工況1）、二期恒載作用（工況2）、系統溫度作用（工況3）、車道荷載作用（工況4）及標準組合作用（工況5）下，取全橋65個節點作為應力分析的關鍵節點。通過空間有限元計算分析，得出控制點的應力響應。各個工況下橋梁測點的應力如圖2和圖3所示。

計算結果表明：在自重作用下，主梁上緣最大應力發生在1#墩墩頂截面，應力大小為24.1MPa，主跨跨中截面上緣應力為-20.7MPa;主梁下緣最大應力發生在第二跨跨中截面，應力值為36.6MPa。在二期恒載作用下，主梁上緣最大應力發生在1#橋墩墩頂截面，應力大小為7.01MPa;主梁下緣最大應力發生在第一跨跨中截面，應力值為-11.2MPa。系統溫度作用對主梁的應力影響均小于0.2MPa。在車道荷載作用下，主梁上緣最大應力發生在第四跨跨中截面，應力為-12.5MPa;主梁下緣最大應力發生在3#橋墩墩頂截面，應力值為-16.2MPa。在標準組合荷載作用下，主梁上緣最大應力為37.2MPa，主梁下緣最大應力為53.4MPa。

綜上所述，在最不利荷載組合作用下，橋梁的應力值為53.4MPa，符合應力要求。在寒冷地區（升/降溫46℃-21℃），溫度對主梁結構的應力影響相對較小。恒載作用下主梁上緣和下緣受到的最大應力分別是車道荷載作用下的2.5倍和2.9倍;恒載作用主梁受到最大應力略大于系統溫度作用下的最大應力。因此，恒載對大跨度連續鋼箱梁橋應力影響最大。

3 主體結構剛度分析

對于變截面連續鋼箱梁橋而言，主梁結構線形是橋梁設計和施工中的重點和難點。考慮5種工況作用下，主梁出現下撓時，撓度值用負號（-）表示，出現向上翹曲時，撓度值用正號（+）表示。各種工況下，主梁線形變化情況如下圖4所示。

計算結果表明：在自重作用下，主梁發生一定變形，產生撓度。其中主梁在第二跨跨中出現最大撓度為-42.3mm;第四跨跨中撓度次之為-21.4mm。二期恒載作用下，主梁最大撓度出現在第二跨跨中位置，下撓值為-12.4mm。溫度荷載作用下，當環境升溫時，橋梁最大向上位移約為0.4mm;當環境降溫時，橋梁最大下撓值為-0.3mm。標準組合作用下，主梁在第二跨跨中位置出下最大下撓為-62.2mm。在各個橋墩附近鋼箱梁出現豎向上翹曲現象，撓度值比較小，其中3#橋墩附近出現5.2mm撓度。

綜上所述，相對恒載和移動荷載對橋梁豎向的線形影響，溫度對橋梁豎向影響較小。恒載和移動荷載作用是橋梁豎向變形的主要影響因素。為了控制主梁運營階段的線性，保證橋梁通行安全，橋梁需要設置適宜的預拱度[14][15]。預拱度的大小宜為結構自重標準值與1/2車道荷載頻遇值產生的撓度值之和[16]。

主梁預拱度設置情況如圖5所示。

由圖5可知：沿縱橋向，各跨主梁設計預拱度采用拋物線的方式進行擬合，各跨預拱度最大值出現在跨中位置，最小值出現在梁端位置。同時發現，第一跨設計預拱度值為6.5mm，第二跨設計預拱度值為64.7mm，第三跨為8.4mm，第四跨設計預拱度值為34.5mm。對于大跨度變截面連續鋼箱梁橋，主跨預拱度值大于邊跨預拱度值。

由圖5可知：沿縱橋向，各跨主梁設計預拱度采用拋物線的方式進行擬合，各跨預拱度最大值出現在跨中位置，最小值出現在梁端位置。同時發現，第一跨設計預拱度值為6.5mm，第二跨設計預拱度值為64.7mm，第三跨為8.4mm，第四跨設計預拱度值為34.5mm。對于大跨度變截面連續鋼箱梁橋，主跨預拱度值大于邊跨預拱度值。

由圖5可知：沿縱橋向，各跨主梁設計預拱度采用拋物線的方式進行擬合，各跨預拱度最大值出現在跨中位置，最小值出現在梁端位置。同時發現，第一跨設計預拱度值為6.5mm，第二跨設計預拱度值為64.7mm，第三跨為8.4mm，第四跨設計預拱度值為34.5mm。對于大跨度變截面連續鋼箱梁橋，主跨預拱度值大于邊跨預拱度值。

4 結論

本文以山區某大跨度變截面連續鋼箱梁橋作為背景，利用Midas Civil中單梁法對橋梁上部主體結構進行靜力計算分析，揭示探析各種荷載工況下變截面連續鋼箱梁橋受力特性和線形變化規律，得出以下結論：

（1）在最不利荷載組合作用下，橋梁的應力值為53.4MPa，符合應力要求。

（2）在寒冷地區（升/降溫460C/-210C），溫度對主梁結構的應力影響相對較小。

（3）恒載對大跨度連續鋼箱梁橋應力影響最大。

（4）相對恒載和移動荷載對橋梁豎向的線形影響，溫度對橋梁豎向影響較小。恒載和移動荷載作用是橋梁豎向變形的主要影響因素。

（5）對于大跨度變截面連續鋼箱梁橋，主跨預拱度值相較于邊跨預拱度值更大。

參考文獻：

[1]徐君蘭， 孫淑紅. 鋼橋.第2版[M]. 人民交通出版社， 2011.

[2]殷飛， 周旭丹. 鋼結構原理與設計[M]. 冶金工業出版社， 2014.

[3]吳沖. 現代鋼橋， 上冊[M]. 人民交通出版社， 2006.

[4]黃震偉， 邢世玲， 徐秀麗，等. 中等跨徑連續鋼箱梁橋上部結構的標準化設計研究[J]. 公路工程， 2017， 42（2）：154-158.

[5]王志明. 淺談橋梁結構分析的計算機方法[J]. 技術與市場， 2012， 19（8）：142-142.

[6]魏華， 劉紅釗， 李煒東，等. 跨線鋼箱梁橋頂推落梁過程的數值模擬[J]. 沈陽工業大學學報， 2017， 39（4）：475-480.

[7]喬治·林德菲爾德， 約翰·彭尼. 數值方法[M]. 機械工業出版社， 2016.

[8]安妮·戈林鮑姆， 蒂莫西P.夏蒂埃， AnneGreenbaum，等. 數值方法：設計、分析和算法實現[M]. 機械工業出版社， 2016.

[9]劉建威， 于鵬， 李德建. S型曲線鋼箱梁橋空間受力特性研究[J]. 鐵道科學與工程學報， 2018（2）.

[10]丁勇， 黃奇， 黃劍源. 連續橋面簡支梁橋靜動力特性的理論分析方法研究[J]. 工程力學， 2015， 32（9）：100-110.

[11]Xiao B， Xie W， Liu H， et al. Establishment of Finite Element Model for Wide Steel Box-Girder Bridge by Modal Test[M]// Environmental Vibrations and Transportation Geodynamics. Springer Singapore， 2018.

[12]Farreras-Alcover I， Chryssanthopoulos M K， Andersen J E. Data-based Models for Fatigue Reliability of Orthotropic Steel Bridge Decks based on Temperature， Traffic and Strain Monitoring[J]. International Journal of Fatigue， 2017， 95：104-119.

[13]洪展坤. 矩形截面薄壁鋼箱梁彈塑性有限元分析[D]. 華南理工大學， 2012.

[14]姚長見. 上跨鐵路鋼箱梁橋轉體施工撓度控制方法分析[J]. 鐵道建筑， 2017（4）：26-29.

[15]張玥， 胡小龍， 武春風. 城市連續鋼箱梁施工預拱度研究[J]. 施工技術， 2015（s2）：251-253.

[16]中交公路規劃設計院有限公司. 公路鋼結構橋梁設計規范[M]. 人民交通出版社， 2015.

基金項目：貴州大學2015年省級本科教學工程建設項目（項目編號：SJJG201517）