基于快速控制電源的IGBT結溫分析

宋德勇，高 格，楊申申

基于快速控制電源的IGBT結溫分析

宋德勇1，高 格2，楊申申1

（1. 中國船舶科學研究中心，江蘇無錫 214082；2. 中國科學院等離子體物理研究所，合肥 230031）

快速控制電源同時運行的IGBT器件數量多，輸出信號需要快速響應不同的給定信號。針對其工作特點，通過理論計算、MATLAB模型及有限元模型仿真，研究了典型工況下IGBT的結溫分布特點，并揭示了該工況下由熱載荷導致的IGBT結構變化，對后續研究IGBT可靠性提供了依據。

快速控制電源；IGBT結溫；有限元

0 引言

EAST裝置為磁約束核聚變托卡馬克裝置，16個RMP線圈被放置在EAST裝置內真空室中來進行邊界局域模等相關研究[1,2]。現有8套完全相同的RMP線圈電源，每套電源為2個串聯的線圈供電[3]。該電源為典型的快速控制電源，響應時間小于0.25 ms。對于1套電源，一共有48個IGBT模塊，即8套電源共384個IGBT模塊。在8套電源同時運行時，研究所有IGBT模塊的可靠性顯得尤為重要，在這種特殊的工況下，需要研究電源中IGBT器件的可靠性相關的參數，而主要工作是分析IGBT的結溫分布[4]。

1 快速控制電源工作模式

快速控制電源拓撲結構為典型的AC-DC- AC結構[5]，AC-DC部分為三相不控整流橋，每個整流橋為一個單獨的DC-AC部分的H橋提供母線電壓，逆變部分主體為H橋兩串三并結構。對于每一個H橋，左右橋臂分別由4個IGBT半橋模塊并聯，IGBT的開關頻率為10 kHz，通過載波移相，等效開關頻率達到120 kHz[6]。

電源的具體輸出參數如表1所示，額定輸出值為4000 A/450 V，延遲時間為從給定信號發出到輸出值上升到額定值的50%時的時間。電源的主要運行工況為脈沖電流和正弦電流，脈沖電流工況下，脈寬、幅值及上升時間均會發生變化，正弦工況下，周期及幅值均會發生變化。

表1 快速控制電源輸出參數

IGBT作為電源中的主要電力電子器件，其失效原因較多，其中熱疲勞最為常見，而高溫導致的失效在所有電子設備失效中所占的比例大于50％[7]，故需要重點分析IGBT的結溫特點。在目前對IGBT可靠性的研究中，主要的壽命預測公式均提到結溫平均值和結溫紋波對壽命的影響[8]，基于本電源的快速響應特點，主要考慮結溫紋波的影響。

2 IGBT結溫分析

2.1 理論計算

根據該型號IGBT數據手冊，額定輸出電流I=4000 A，母線電壓U=340 V，開關頻率f=10 kHz，負載直流阻抗R=32 mΩ，假定并聯的IGBT之間不均流度=6%，并聯支路不均流度=5%，計算方法[9][10]如式(1)-(8)所示：

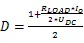
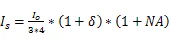
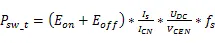
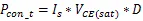
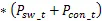
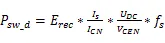
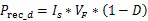
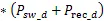
上述公式中，I為單個IGBT的電流，為IGBT占空比，P和P為IGBT的開關損耗和通態損耗，分別為245.65 W和351.14 W，P和P為二極管的開關損耗和反向恢復損耗，分別為64.59 W和228.17 W，?T和?T分別為IGBT和二極管的結溫溫升，結果為70.42 K和58.55 K。

上述計算可以看出IGBT和二極管結溫溫升平均值主要取決于輸入電流值、工作電壓、開關頻率以及電流的占空比，輸入電流、工作電壓越大，則IGBT和二極管的工作條件越苛刻，其結溫溫升會越高；開關頻率越高，說明電子器件動作越頻繁，開關損耗會越高，導致IGBT和二極管的結溫溫升越高；占空比越大，說明IGBT每個電流周期內工作時間越長，其結溫溫升也會越高，同時二極管結溫溫升越低。

2.2 MATLAB模型仿真

2.2.1 單脈沖工況

如圖1所示，由熱阻抗等效圖，可將IGBT的熱阻模型等效為電路模型[11]，在MATLAB中搭建電路進行仿真，熱阻抗參數如表2所示。

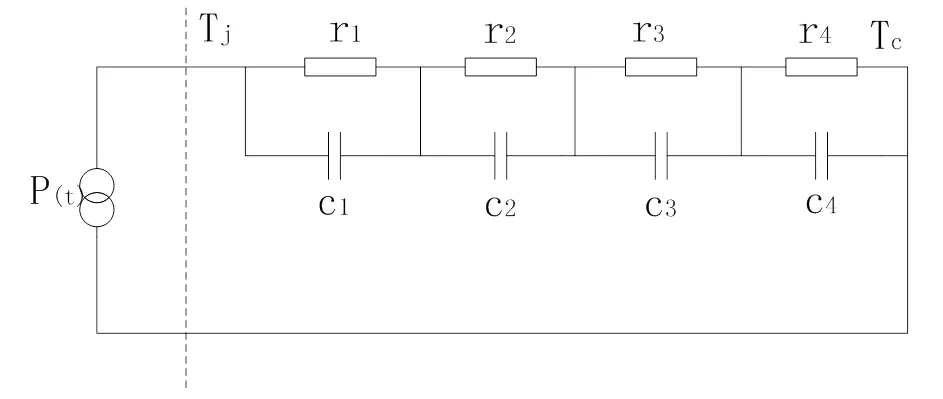
圖1 IGBT模塊熱阻抗等效圖

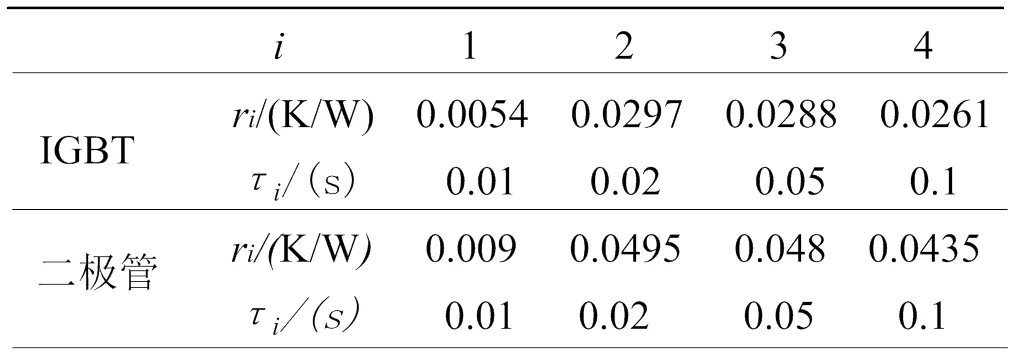
表2 IGBT模塊熱阻抗參數

如圖2所示，輸出直流4000 A電流時，IGBT管芯最高溫升為70.16 K，二極管管芯最高溫升為58.68 K，變化趨勢均與瞬態阻抗曲線一致，仿真結果也與理論計算一致。為了考察IGBT模塊瞬態情況下的承受電流能力，只需分析IGBT的溫升即可。

2.2.2 多周期脈沖工況

IGBT結溫的上升是由于工作時的功率損耗引起的[12]，幅值為P的矩形單脈沖或間隔時間足夠長的連續脈沖作用于IGBT芯片時，所引起的IGBT結溫T自初始溫度T的變化如圖3所示。

結溫經過足夠長的時間能回到初始溫度，但是，當IGBT處在連續導通一串脈沖的PWM工作方式下，且連續脈沖的間隔時間不足以使結溫恢復到初始值，此時IGBT結溫在連續脈沖的反復作用下累積疊加上升，在經過一個逐步上升的過程后，結溫圍繞著一個恒定的平均溫度T做近似等幅波動，此時熱量的產生與散失達到了動態平衡[13]。

圖2 IGBT模塊結溫溫升曲線

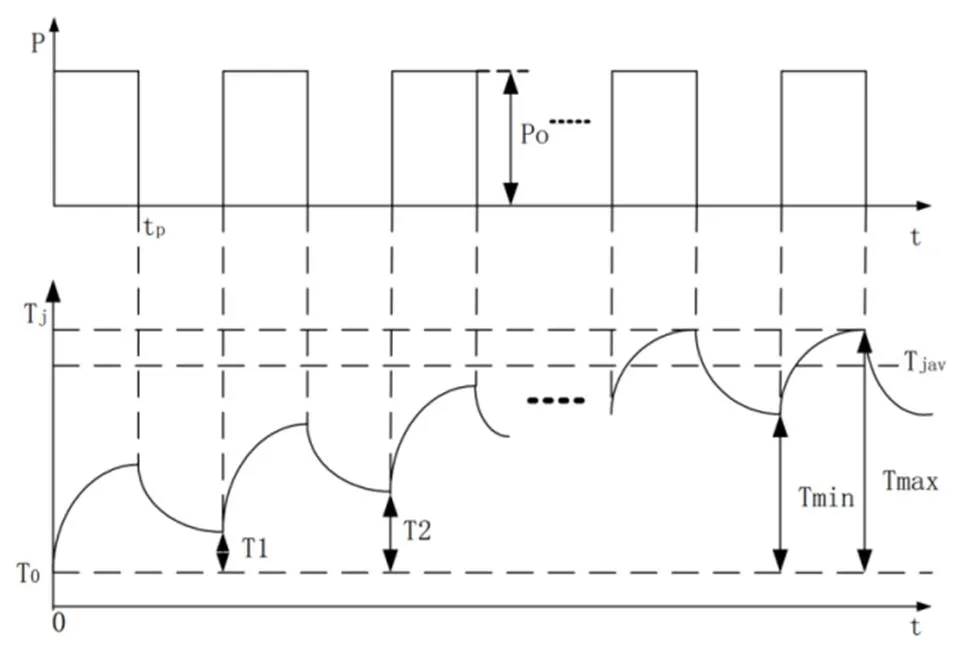
圖3 結溫疊加上升過程

假定此脈沖功率周期為0，每個周期內脈沖作用時間為tp，無脈沖時間為t，將初始殼溫0作為零刻度，脈沖功率不作用期間結溫只是零輸入響應，脈沖功率作用期間結溫是一個零輸入響應和一個零狀態響應相加的全響應[14]。

根據IGBT的熱阻熱容等效為電路中的電阻電容，將脈沖功率作為一個電流源激勵，結溫在受到功率脈沖周期作用后的變化[15]如下：

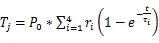
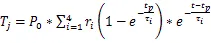
第一個脈沖周期結束后結溫：

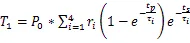
以此類推，第n個脈沖周期結束后結溫：

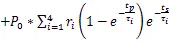
當n→∞，結溫進入穩定的等幅波動狀態，遞推可得，第n個脈沖周期結束后結溫：

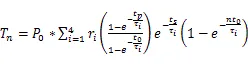
在任意一個周期內的結溫：

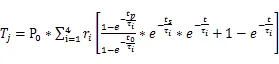
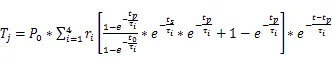
結溫最小值、最大值、紋波：

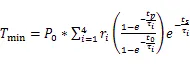
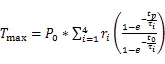
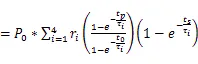
由圖4可以看出，脈沖功率值恒定時，IGBT結溫紋波與輸入電流周期及占空比都有關。

輸入電流周期固定時，占空比在從0增大到1的過程中，結溫紋波初始階段增大，進入一段時間的平頂部分然后又逐漸減小，整體呈對稱變化趨勢，同時輸入電流周期越小，其結溫紋波的絕對最大值也越小，且結溫紋波到達最大值的時間越長，具體二維曲線如圖5所示。

占空比固定時，輸入電流周期越大即頻率越低時，結溫紋波越大，且結溫紋波在占空比為0.5時上升最快，在占空比小于或大于0.5時上升均變慢，并呈對稱分布，具體二維曲線如圖6所示。

設定環境溫度為30℃，在MATLAB仿真模型中改變輸出電流頻率和占空比，得到如表3所示結果。在僅有輸出電流頻率發生改變時，溫升平均值不變，但結溫紋波發生變化，頻率越低，結溫紋波越大，這與理論分析完全一致。

圖5 不同電流周期下IGBT結溫紋波與占空比關系

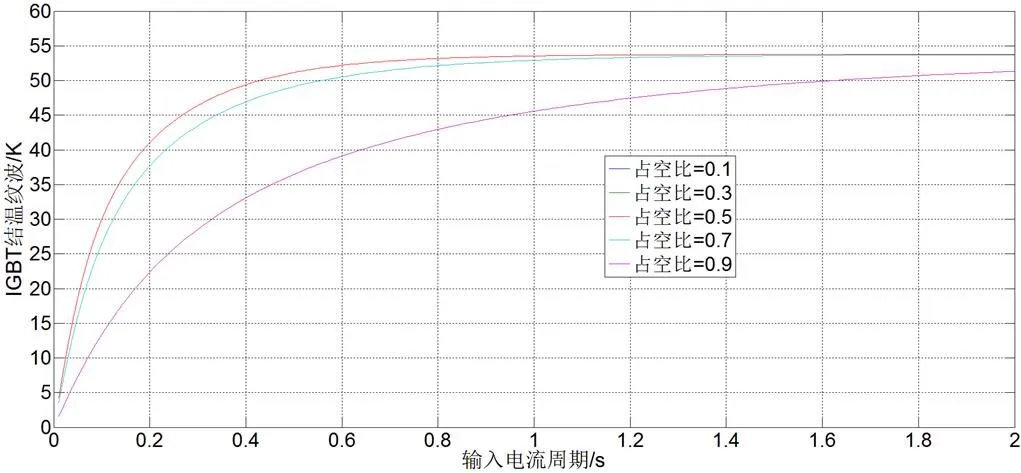
圖6 不同占空比下IGBT結溫紋波與電流頻率關系

表3 不同頻率電流下IGBT結溫

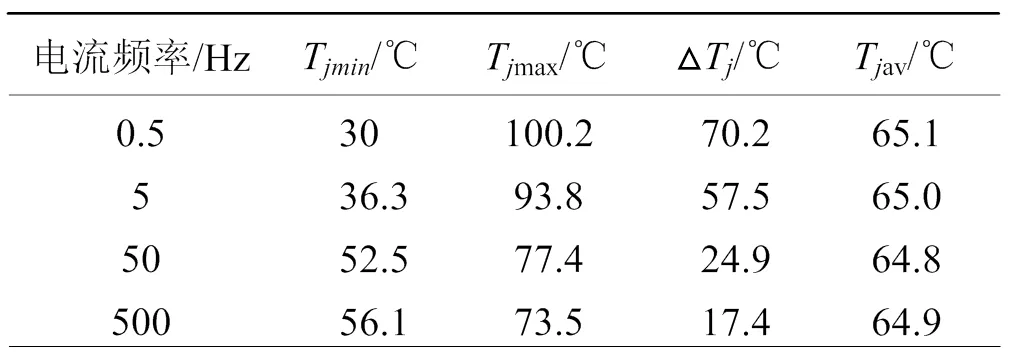
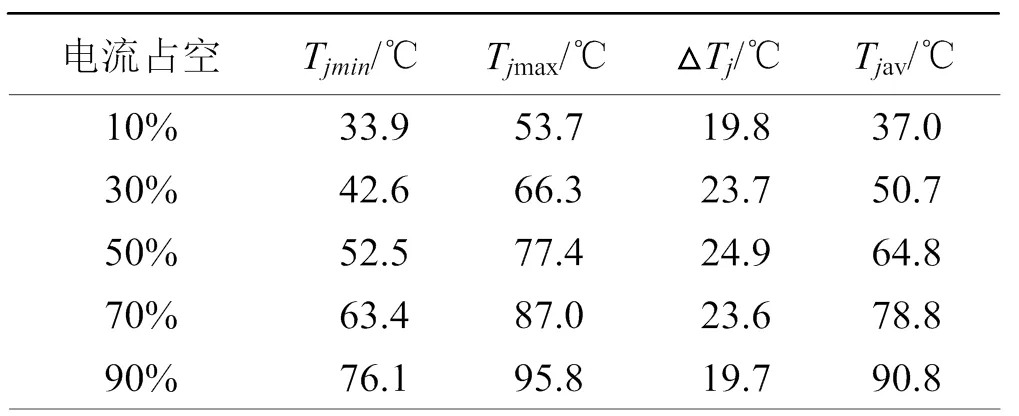
如表4所示，在僅有占空比發生改變時，器件的溫升平均值隨占空比的增大而增大，同時器件的結溫紋波在占空比為0.5時為最大，在低于或高于0.5時均呈下降趨勢，關于占空比為0.5時的結溫紋波呈對稱分布，與理論分析一致。

表4 不同占空比電流下IGBT結溫

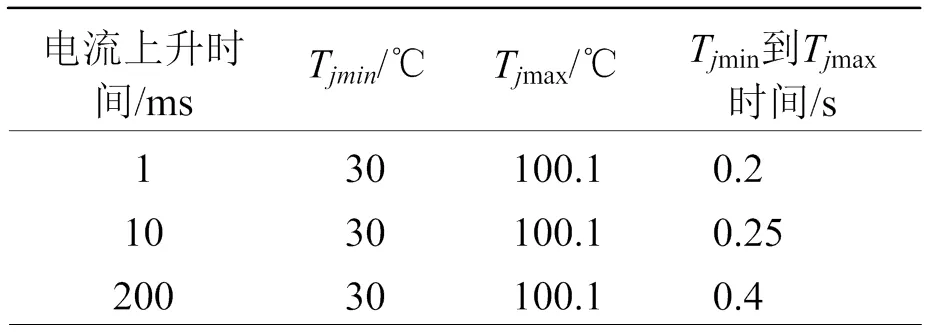
如表5所示，同頻率的脈沖電流，在電流上升時間變長時，IGBT結溫從最小值到最大值的上升時間變長，即IGBT由脈沖電流工況向近似正弦電流工況轉變。

2.3 有限元模型仿真

針對型號為英飛凌FF600R06ME3的IGBT模塊，建立其三維模型[16]，由封裝模型簡化為最簡單的分層模型，以有限元的思想，在workbench中進行熱-結構耦合分析[17,18]，圖7為此IGBT的分層結構示意圖。

表5 不同上升時間電流下IGBT結溫

由于該IGBT內部由3個完全相同的部分組成，實際仿真時提取其三分之一。根據計算，在4000 A情況下，IGBT總損耗為596.79 W，故對一個IGBT芯片上表面施加5 Hz的200 W功率，銅底板下底面設定對流換熱系數[19]為4320 W/(m2*℃)，其它面為絕熱，環境溫度為30 ℃，瞬態加熱時長為2 s。

在瞬態條件下，IGBT 結溫曲線如圖8所示，紅色曲線為最低溫度，綠色曲線為最高溫度，最高溫度位于被加熱的IGBT芯片上表面，為86.15 ℃，結溫紋波為56.15 ℃，與上述結溫仿真結果(57.5 ℃)基本一致。

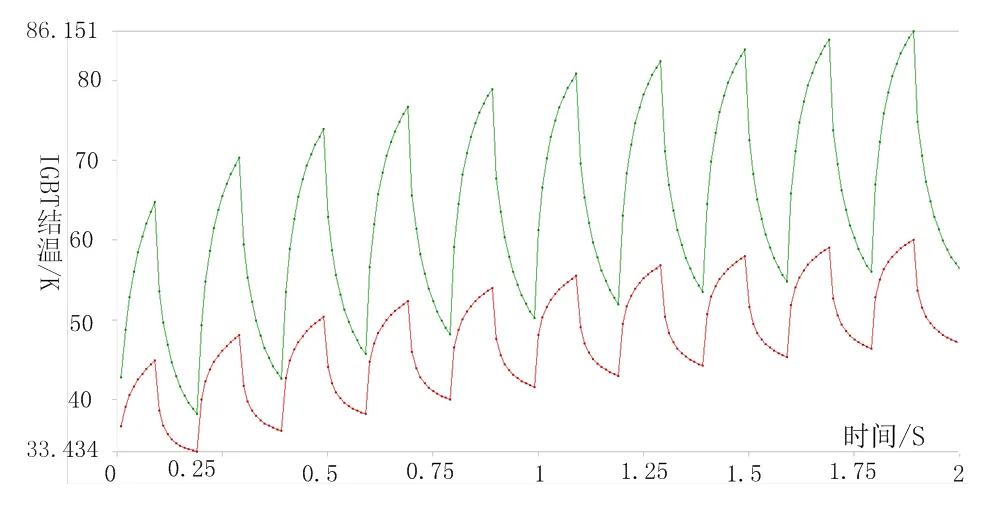
圖8 IGBT結溫曲線

IGBT模塊的應力分布從芯片到底板呈現出非線性變化，且形變最大值為11.59 μm，出現在鍵合線處，如圖9所示，說明在瞬態加熱功率條件下，鍵合線容易首先變形，使其與芯片上表面間的接觸不牢固，出現斷裂現象，這是因為鍵合線的熱膨脹系數遠大于IGBT芯片，在受到周期性熱應力沖擊時，由于兩者之間熱膨脹系數匹配較差，熱應力長期沖擊最終導致鍵合線失效。

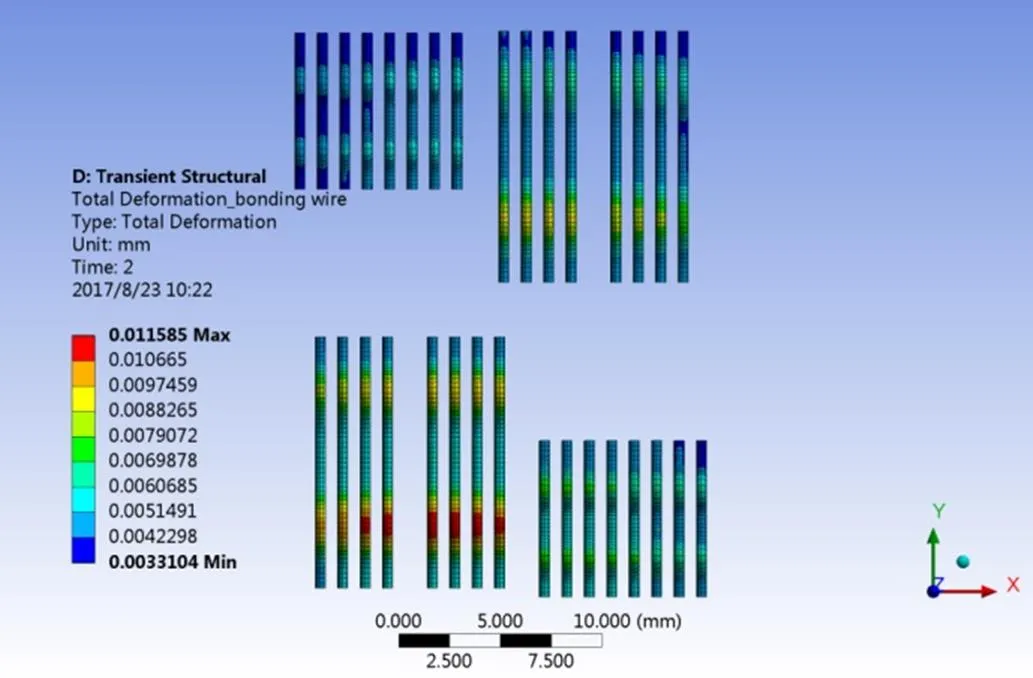
圖9 IGBT模塊形變分布

3 總結

EAST裝置上應用于快速控制電源的IGBT工況非常特殊，實際工作時輸出電流的幅值、頻率、占空比和上升時間均會發生變化，在不同的工況下，IGBT的結溫平均值和結溫紋波會發生變化。

綜上所述，脈沖工況需要考慮上升時間、電流頻率、電流幅值、開關頻率和占空比5個因素對結溫溫升或結溫紋波的影響，這也是影響IGBT可靠性的因素，且脈沖工況下IGBT鍵合線的形變最大，是失效的主要環節。長上升時間、高電流頻率、低電流幅值、低開關頻率和低占空比更有利于延長IGBT的使用壽命。實際應用時，開關頻率、電流幅值基本不變，因此需要重點關注上升時間、電流頻率和占空比對IGBT壽命的影響。

[1] 郝長端．J_TEXT托卡馬克共振磁擾動線圈的電磁結構分析和熱分析[D]．武漢: 華中科技大學，2011．

[2] V．Toigo, E．Gaio, R．Piovan, et al． Overview on the power supply systems for plasma instabilities control[J]．Fusion Engineering and Design, 2011, 86: 565-571．

[3] 宋德勇, 高格, 傅鵬等. EAST裝置RMP線圈電源的優化設計[J]．核聚變與等離子體物理, 2017, 37(2): 199-203．

[4] 周雒維, 吳軍科, 杜雄等. 功率變流器的可靠性研究現狀及展望[J]．電源學報, 2013, 1: 1-15．

[5] Deyong Song,Peng Fu,Ge Gao, et al．The Harmonic Analysis of RMP Coil Power Supply in EAST TOKAMAK [J]．Journal of Fusion Energy, 2016, 35(3): 550-555．

[6] 宋德勇. EAST托卡馬克共振磁擾動線圈電源設計分析研究[D]. 合肥: 中國科學技術大學, 2017.

[7] 潘洋. IGBT封裝模塊散熱特性的研究[D]．武漢: 華中科技大學, 2013．

[8] 賴偉, 陳民鈾, 冉立, 等. 老化實驗條件下的IGBT壽命預測模型[J]．電工技術學報, 2016, 31(24): 173-180．

[9] 謝勤嵐, 陳紅. PWM逆變器中IGBT的損耗計算[J]．中南民族大學學報, 2003, 22(1): 39-41．

[10] 張明元, 沈建清, 李衛超等. 一種快速IGBT損耗計算方法[J]．船電技術, 2009, 29: 33-36．

[11] 魯光祝. IGBT功率模塊壽命預測技術研究[D]．重慶: 重慶大學, 2012．

[12] 陳明, 胡安, 唐勇等. 絕緣柵雙極型晶體管脈沖工作時結溫特性及溫度分布研究[J]．西安交通大學學報, 2012, 46(4): 70-76．

[13] 劉輝. 等離子體垂直位移快速控制電源關鍵技術研究[D]．北京: 中國科學院大學, 2014．

[14] 顏秋容, 譚丹. 電路理論[M]．北京: 電子工業出版社, 2009．

[15] 侯少敏. 高速動車組變流系統損耗分析與散熱研究[D]．北京: 北京交通大學, 2011．

[16] 余小玲. 電力電子集成模塊及新型翅柱復合型散熱器的傳熱性能研究[D]．西安: 西安交通大學, 2005．

[17] 熊文雯, 張小玲, 謝雪松等. 基于結構函數的IGBT熱特性研究[J]．電力電子技術, 50(12), 11-14, 2016．

[18] 張薷方. 基于有限元法的IGBT模塊封裝散熱性能及熱應力的仿真研究[D]．重慶: 重慶大學, 2015．

[19] 陳永淑. IGBT的可靠性模型研究[D]．重慶: 重慶大學, 2010．

Analysis of IGBT Junction Temperature Based on Fast Control Power Supply

Song Deyong1, Gao Ge2, Yang Shenshen1

(1. China Ship Scientific Research Center, Wuxi 214082, Jiangsu, China; 2. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China)

TN86

A

1003-4862（2019）10-0001-05

2019-04-19

國家磁約束核聚變能發展研究專項 (基金編號2013GB102003)

宋德勇（1990-），男，工程師。研究方向：電力電子器件應用。E-mail: dysong1990@163.com