擺火柴棒的規律

◎馬濟敏

擺火柴棒，可以從中發現規律，是一種好玩的數學游戲。

例1：用火柴棒擺圖案，按下面規律擺下去，第n個圖案需要火柴棒多少根？

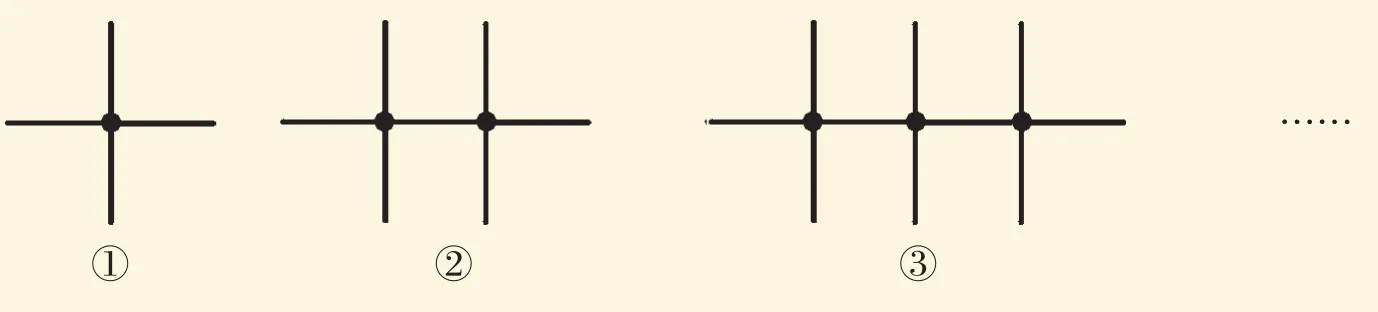
思路點睛：觀察圖形，數一數，我們發現第1個圖形有4根火柴棒，第2個圖形有7根火柴棒，第3個圖形有10根火柴棒……這些數字之間有什么規律呢？這就需要我們有一雙“火眼金睛”，對照圖形的特點對這些數字進行分析，然后發現規律。如果先擺出1根火柴棒，則有：

第1個圖形，有1+3=4根火柴；

第2個圖形，有1+3+3=7根火柴；

第3個圖形，有1+3+3+3=10根火柴；

…………

規律出現了，有幾個圖形，就有1＋幾個3根火柴棒，所以，第n個圖形有1+3+3+…+3=3n+1根火柴棒。故答案為：第n個圖案需要火柴棒3n+1根。

例2：如圖，用火柴棒擺出一列正方形圖案，若按這種方式擺下去，擺第n個圖案用多少根火柴棒？（用含n的式子表示）

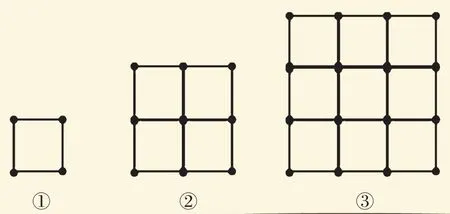
思路點睛：對于找規律的題目，首先應找出哪些部分發生了變化，是按照什么規律變化的，然后分析得出規律。

圖①，4根火柴棒；圖②，12根火柴棒；圖③，24根火柴棒。我們先對這三組數字進行研究。

圖①，4=1×4；

圖②，12=4×3=4×（1＋2）；

圖③，24=4×6=4×（1＋2＋3）。

再畫一個邊長是4的正方形驗證一下：

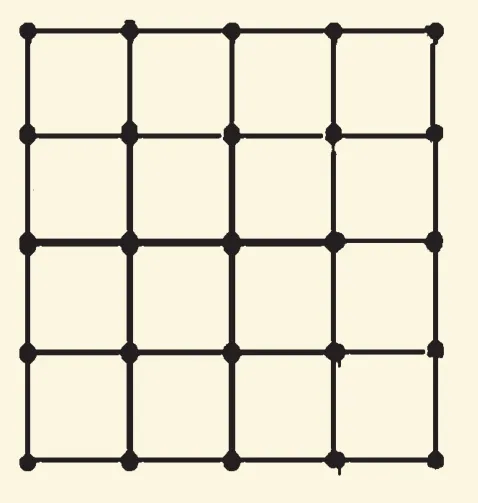
需要40根火柴棒，40=4×10=4×（1＋2＋3＋4），符合發現的規律。所以第n個圖案，需要火柴棒：4×（1＋2＋3＋…＋n）=2n×（n＋1）根。

請你也來練一練：

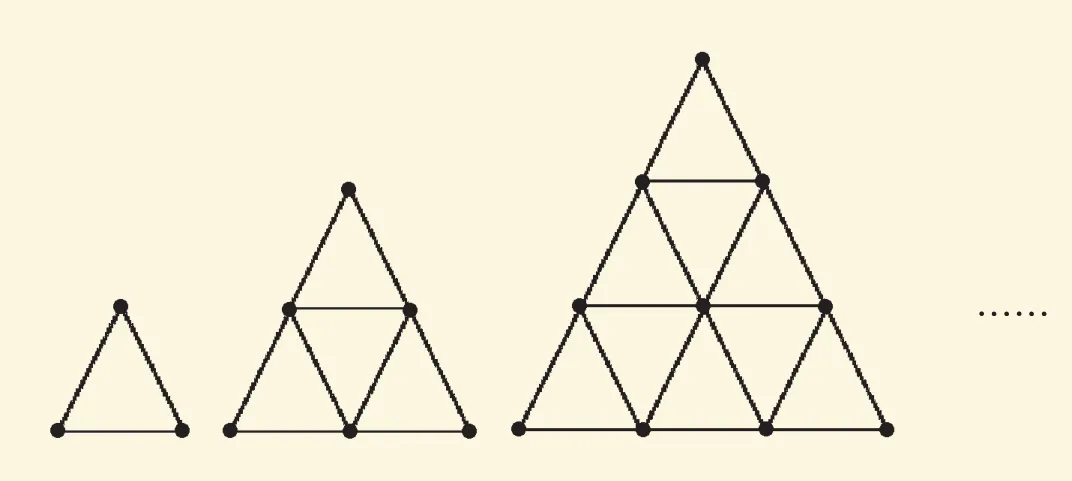
如圖，用火柴棒按下列規律擺三角形，第5個圖形需火柴棒（ ）根；擺第15個圖形時，需要火柴棒（ ）根。

《擺火柴棒的規律》參考答案

3×（1＋2＋3＋4＋5）=45（根）

3×（1＋2＋3＋…＋15）=360（根）