Elandt-Johnson模型推算完全壽命表方法學原理及其在中國人群壽命表中的應用*

國家癌癥中心/國家腫瘤臨床醫學研究中心/中國醫學科學院北京協和醫學院腫瘤醫院(100021)

安 瀾 鄭榮壽 張思維 楊謹成 孫可欣 曾紅梅△

【提 要】 目的 介紹Elandt-Johnson模型法推算完全壽命表的方法學原理，并應用該方法推算中國完全壽命表。方法 以全國第六次人口普查結果2009年11月1日至2010年10月31日分年齡、性別的死亡率為實例構建真實完全壽命表，計算出簡略壽命表，然后以簡略壽命表為基礎數據，采用Elandt-Johnson模型法推算理論完全壽命表，并與真實完全壽命表比較以評估模型擬合效果。結果 采用Elandt-Johnson模型推算出的男女分年齡死亡率與真實死亡率擬合優度良好，決定系數R2分別為0.9966和0.9994。依據理論完全壽命表估算出的預期壽命(男性72.43，女性77.23)與真實完全壽命表計算出的預期壽命非常接近(男性72.38，女性77.30)。結論 Elandt-Johnson模型法可以將簡略壽命表推算出較為準確的完全壽命表。

壽命表是根據特定人群的年齡組死亡率編制出的一種統計表，用以說明在特定人群年齡組死亡率條件下人的生命過程[1]。壽命表是社會科學的重要工具、并在科研中廣泛運用，是用于計算預期壽命的基礎。完全壽命表是按每個年份、一歲一個年齡組和性別來計算死亡概率和死亡率。簡略壽命表習慣以5歲一組，由于0～歲組嬰兒死亡率對壽命表的影響相當大，簡略壽命表將0～4歲拆分為0～，1～歲組。在很多情況下，簡略壽命表因其構造簡單被廣泛運用[2]。一方面是因為簡略壽命表是按照5歲年齡組劃分而計算的死亡率，數據相對穩定；另一方面由于各地區全死因登記數據質量問題，在無法獲得穩定而完整的完全壽命表資料時，死因數據結果常以簡略壽命表資料呈現。在計算人群癌癥相對生存率時，我們需要根據完全壽命表計算分年齡、性別和時期的預期生存概率[3]。由于從我國部分腫瘤登記地區難以獲得精準的完全壽命表資料，部分死因監測地區僅提供簡略壽命表數據[4]，因此需要在缺乏完全壽命表的情況下，采用科學的方法將簡略壽命表資料推算成完全壽命表。

本文介紹Elandt-Johnson模型法將簡略壽命表推算至完全壽命表的原理，并根據用漏報方法調整的我國第六次全國人口普查數據建立簡略壽命表和完全壽命表，運用該方法將簡略壽命表推算出完全壽命表，將推算出的完全壽命表與真實完全壽命表進行比較，評價Elandt-Johnson模型推算完全壽命表的效果。

數據來源和方法

1.數據來源

本研究使用2009年11月1日至2010年10月31日全國分性別1歲一個年齡組的死亡率數據。數據來源于國家統計局公布的2010年第六次全國人口普查資料各地區分年齡、性別死亡人口狀況(2009年11月1日-2010年10月31日)[5]。采用國家統計局公布的死亡人口漏報率調整年齡別死亡率[6]。

2.預期壽命計算方法

本研究利用壽命表法，利用第六次人口普查數據庫中提供的分年齡組平均人口數、實際死亡人數，計算各年齡組死亡率。采用黃榮清[7]等人的嬰兒死亡率估計值(男性為16.85‰，女性為17.69‰)修正0歲組死亡率，使用國家統計局公布的死亡人口漏報率18.4%修正其他年齡別死亡率，得出調整年齡別死亡率和死亡概率[6]。假設0歲組人數為10萬人，以調整年齡別死亡率計算各年齡組死亡人數、生存人數、生存人年數和累積生存總人年數，最后算得各年齡組預期壽命。

(1)年齡分組nx：簡略壽命表分為0歲組(x=0，n=1)，1～4歲(x=1，n=4)，5～9歲(x=5，n=5)，10～14，…，95+；完全壽命表1歲一組(n=1)。

(1)

(2)

(4)年齡組死亡概率nqx：

nqx=1-e-nx×nMx’

(3)

(5)x歲年齡組總死亡人數dx：

dx=lx×qx

(4)

(6)x歲年齡組總生存人數lx：

令l0=100000，lx+1=lx-dx

(5)

(7)生存人年數Lx：

(6)

(8)x歲年齡組生存總人年數Tx：

(7)

(9)x歲年齡組的預期壽命ex：

(8)

3.Elandt-Johnson模型推算法

Elandt-Johnson模型推算法是利用三個不同年齡段所對應的三種插值函數與平滑公式，將簡略壽命表資料推算至完全壽命表[8]。推算過程是先由簡略壽命表中的生存人數AlX推算完全壽命表中的生存人數ClX，進而推算出完全壽命中各年齡組死亡率。生存人數的計算根據年齡分為三組：

(1)0～9歲組：采用六點拉格朗日內插公式進行推算。對于簡略壽命表中的Alx將使用表1的系數推算完全壽命表中的Clx(x<10)[8]，即我們用l1、l5、l10、l15、l20和l25的數值進行線性內插計算。線性內插法可以確保在推算出的完全壽命表中保留了簡略壽命表中的原始數據[9]。舉例如下：

Cl2=0.562030l1+0.717600l5-0.478400l10+0.282886l15-0.100716l20+0.015600l25

(2)10～74歲組：采用六點拉格朗日內插公式進行推算。對于10歲～74歲年齡組的系數，將使用表2的系數進行線性內插計算[8]。舉例如下：

Cl11=0.008064l0-0.073920l5+0.887040l10+0.221760l15-0.049280l20+0006336l25

(3)75歲及以上組：75歲及以上人群推算采用龔帕茲Gomepertz生存曲線擬合法估計[10-11]。

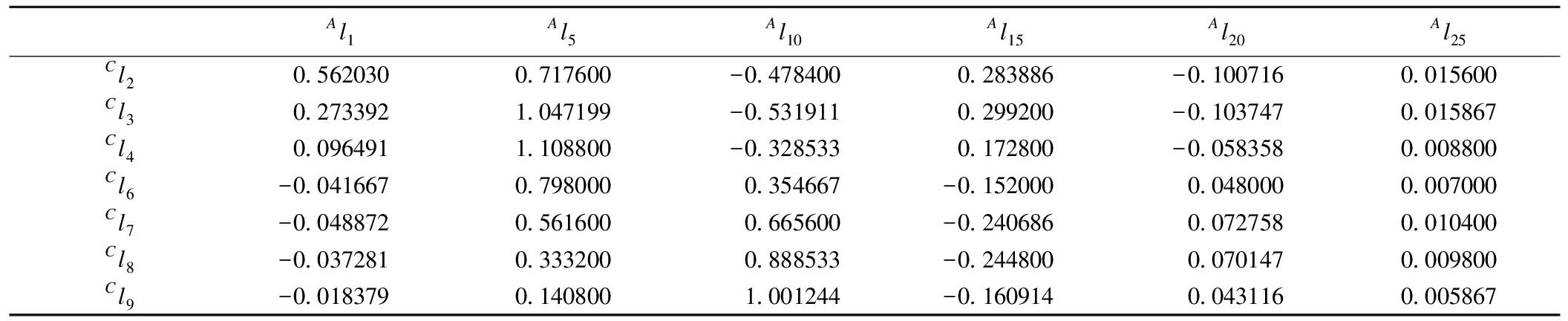
表1 計算完全壽命表Cl2-Cl9的系數

表2 計算完全壽命表Cl11-Cl74的系數

*：m=2時，可計算Cl11-Cl14；m=3時，可計算Cl16-Cl19；以此類推，m=14時，可計算Cl71-Cl74。

龔帕茲生存公式為：

(9)

x1和x1+5成為lx兩個接點可得出，

(10)

代入(9)公式計算得出

lx1=b1-cx1,lx1+5=b1-cx1+5

同樣，對于x2和x2+5

(11)

(12)

結合公式(10)

(13)

用公式(12)和(13)得出各年齡x的參數b和c(參數a和R的函數)。再結合公式(9)計算出各年齡組生存人數lx：

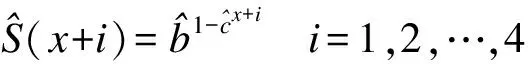
4.應用軟件

應用SAS 9.2軟件編制壽命表計算預期壽命，應用STATA 13.0軟件實現Elandt-Johnson模型推算，采用Excel軟件繪圖并計算推算出的完全壽命表數據與真實完全壽命表數據的擬合程度。

結 果

表3以全國各年齡組平均人口數和漏報調整死亡人數為例，展示了2010年中國分性別簡略壽命表的基本指標，根據壽命表法計算的分性別、分年齡組死亡概率、預期壽命見表3。

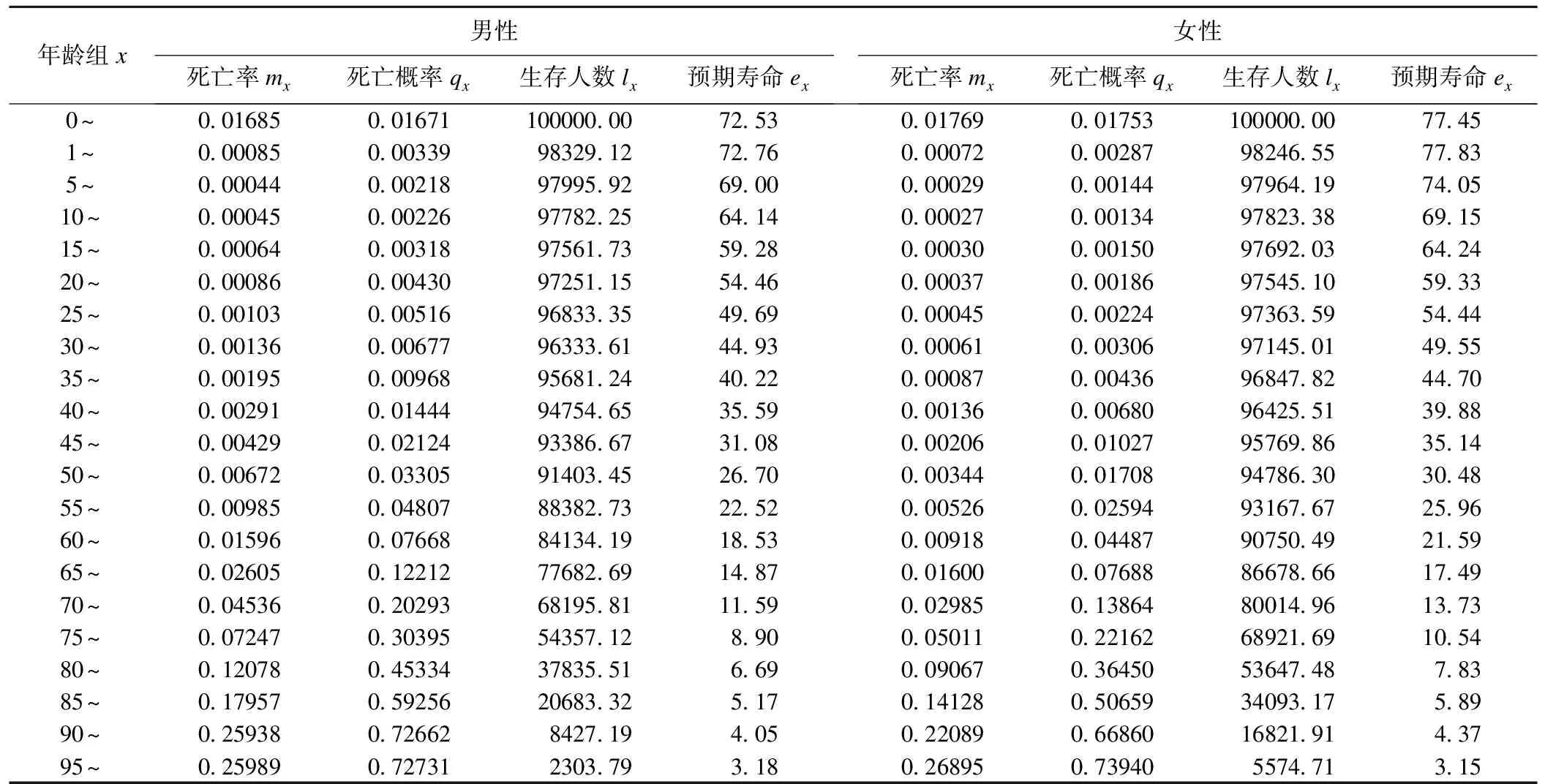
表3 2010年中國分性別簡略壽命表

表4給出完全壽命表及Elandt-Johnson模型推算出的完全壽命表中的死亡率、死亡概率以及預期壽命。完全壽命表結果顯示2010年中國男性預期壽命為72.38歲，Elandt-Johnson模型推算結果為72.43歲；中國女性預期壽命為77.30歲，Elandt-Johnson模型推算結果為77.23歲。各指標值見表4。

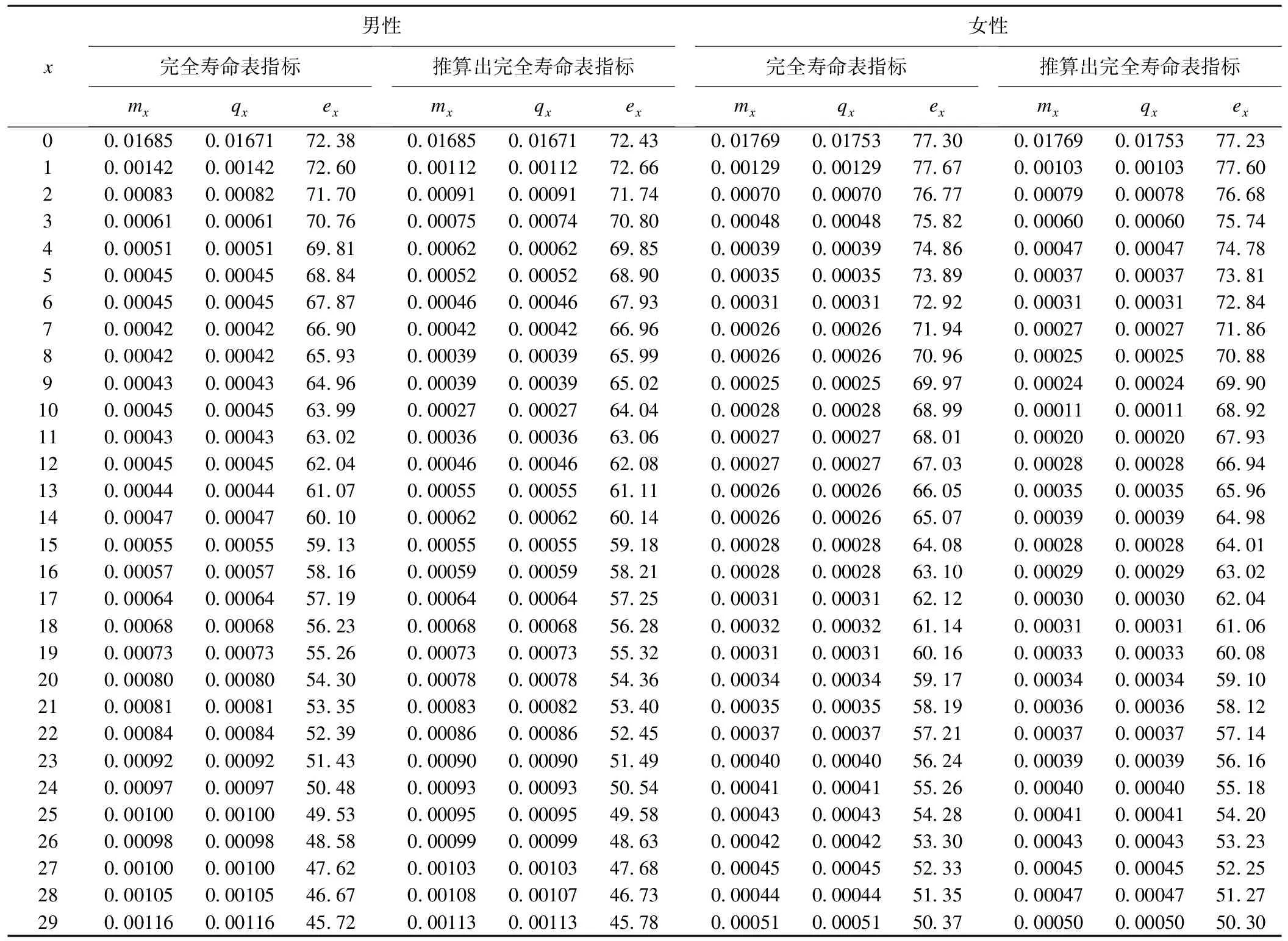
表4 2010年中國分性別完全壽命表及Elandt-Johnson模型推算出的完全壽命表

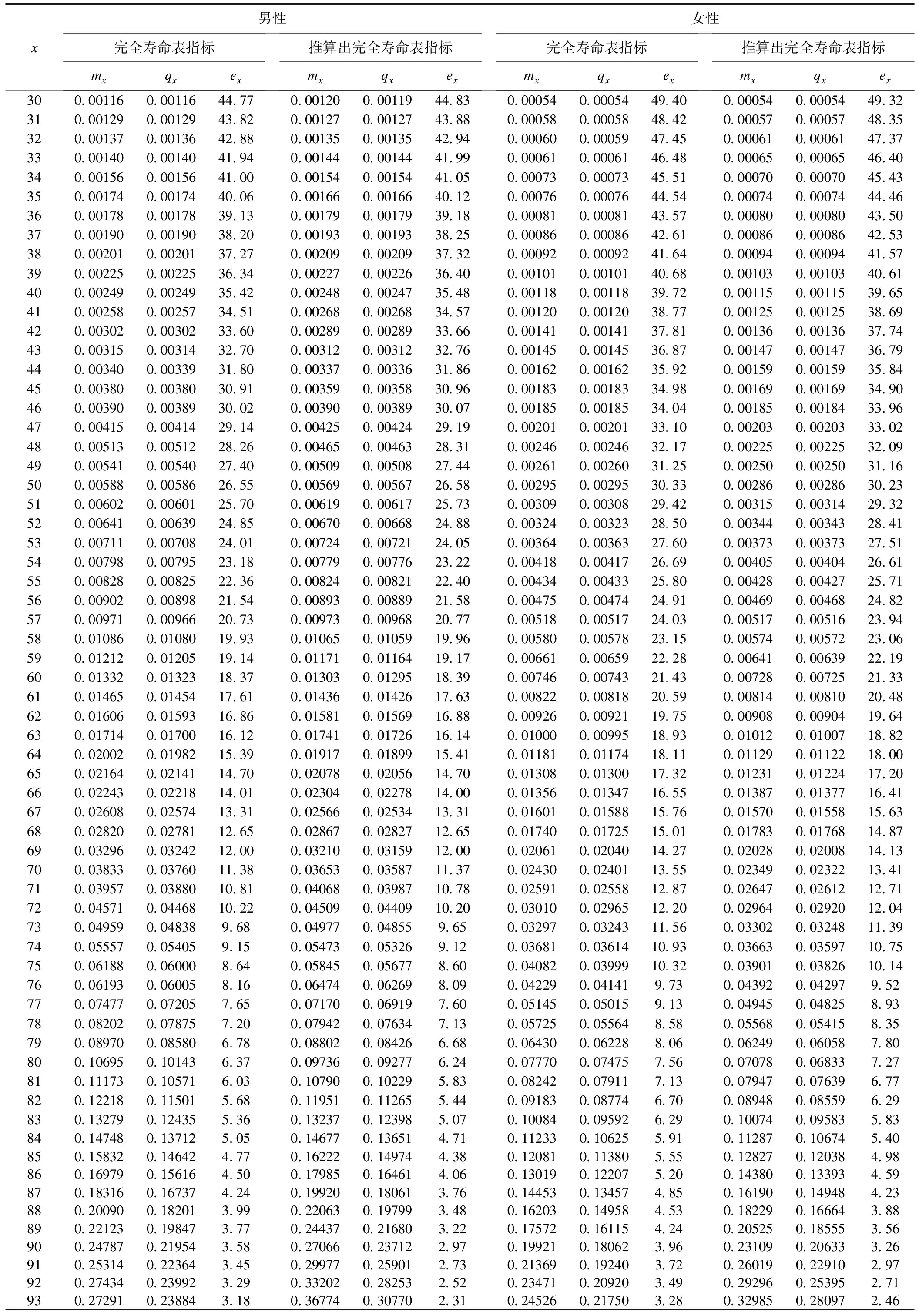
續表4

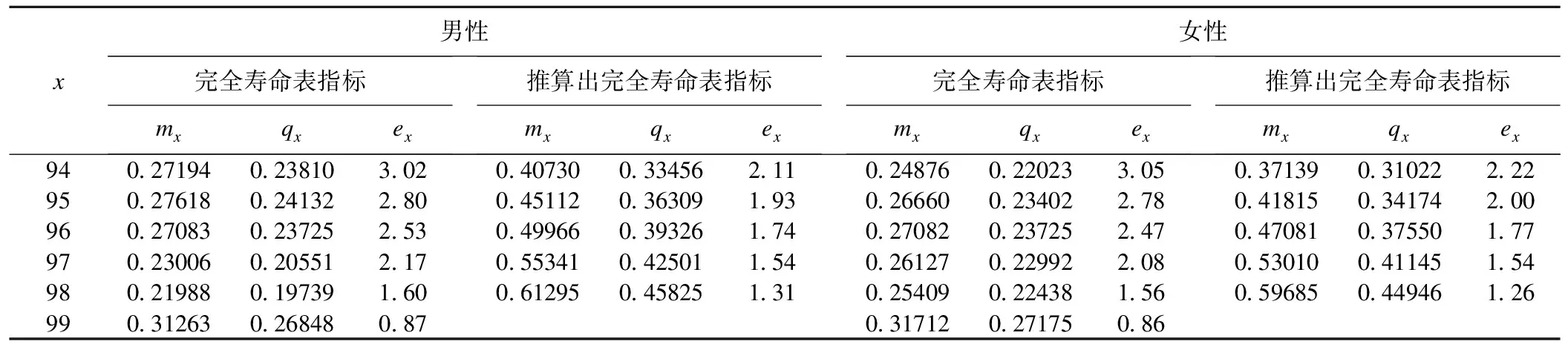
續表4

圖1表示2010年中國男性與女性真實死亡率與擬合死亡率的相關程度，分別采用線性回歸模型和二次多項式回歸模型計算擬合死亡率與真實死亡率間的擬合優度，結果顯示男性擬合死亡率與真實死亡率間決定系數R2為0.9966，女性R2為0.9994，均優于線性擬合曲線R2，二次多項式模型為最優擬合模型。圖2為2010年中國兩性各年齡組死亡率與推算出完全壽命表中擬估計年齡組死亡率的半對數線圖。可以看出0～10歲死亡率呈現下降趨勢，表示該年齡段的死亡率相對水平在逐步下降，其中0歲組死亡率最高，符合壽命表年齡組死亡率的特點，10歲以上年齡組死亡率呈現上升趨勢。各年齡組死亡率與推算出的年齡組死亡率曲線擬合效果良好。圖3表示2010年中國分性別分年齡生存人數與推算出的擬估計生存人數的擬合程度。可以看出各年齡組生存人數基本上與推算出的年齡組生存人數的曲線貼合，且該曲線的曲度、高度符合一般規律，即0～65歲年齡段曲線較平緩，生存人數減少較慢，65歲之后曲線較陡峭，生存人數減少較快，死亡概率較高。從圖中可以看出，女性各年齡段生存人數均高于男性，可解釋女性預期壽命高于男性。

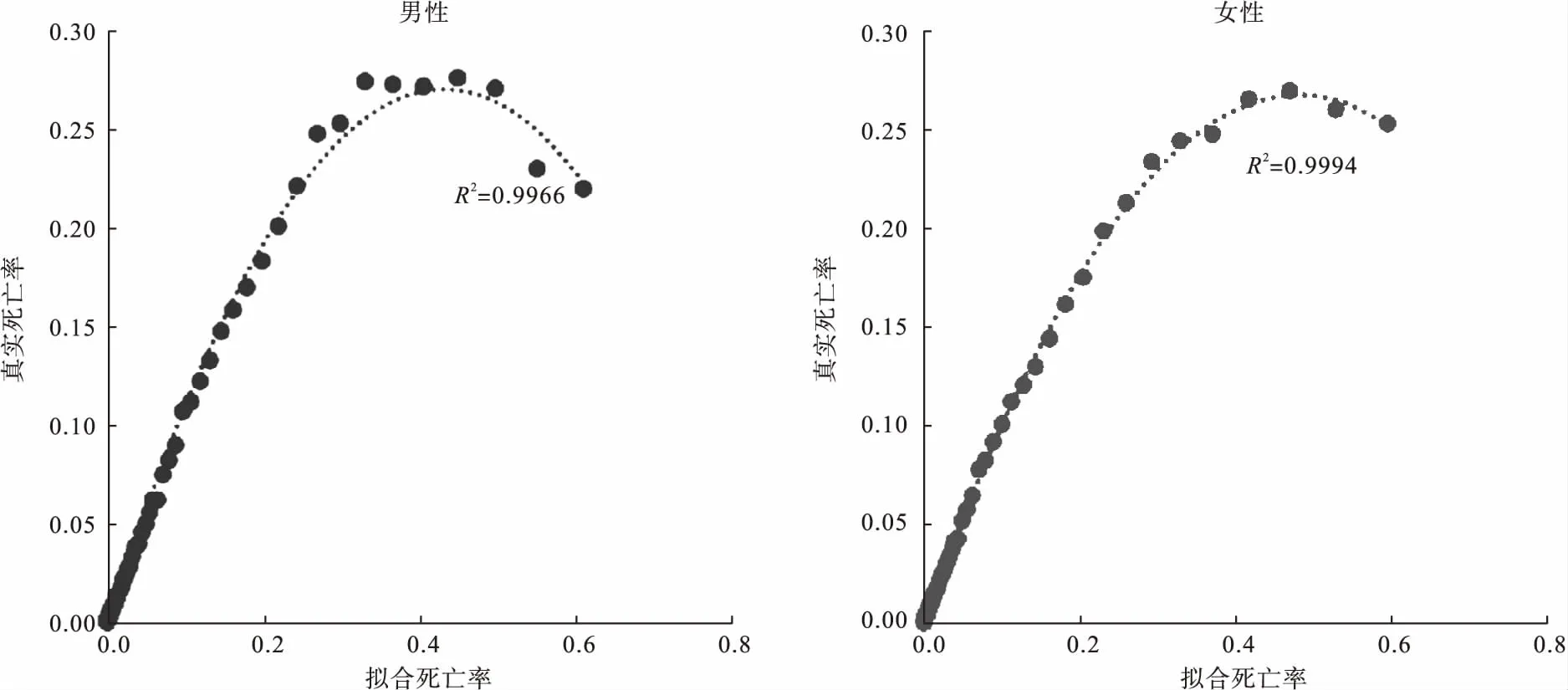
圖1 2010年中國分性別分年齡真實死亡率與模型推算出死亡率的擬合曲線

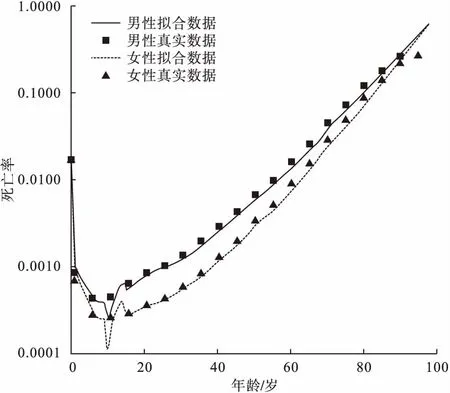
圖2 2010年中國分性別分年齡死亡率與模型推算出死亡率的擬合曲線

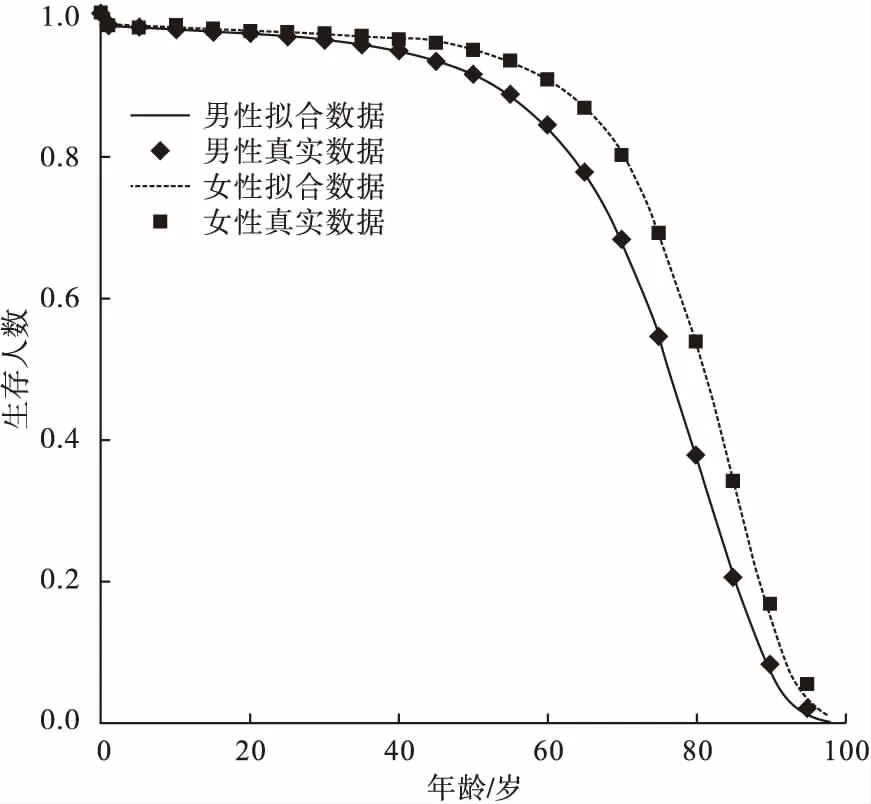
圖3 2010年中國分性別分年齡生存人數與模型推算出生存人數的擬合程度

討 論

壽命表是評價地區人口健康狀況的綜合性指標[12]，它可以提供不同人群完整的死亡信息[13]，且其在時間、空間的縱橫比較上具有良好的可比性[14]。壽命表提供的預期壽命指標是衡量國家或地區社會發展的重要指標[15]。編制完全壽命表時，觀察人數要足夠多，因為完全壽命表分組細，各年齡組死亡率又低，在某些人口較少地區因為觀察人數不夠多，容易出現年齡組死亡率不夠穩定的現象；簡略壽命表年齡分組少，每個年齡組人數較多，年齡組死亡率比較穩定，因此人口較少的地區簡略壽命表較為常見。簡略壽命表只能提供有限的死亡信息，有時難以滿足精細化的分析需求，如何科學地依據簡略壽命表構建完全壽命表就顯得尤為重要[16]。

Elandt-Johnson模型法是依據簡略壽命表推算出完全壽命表的一種常見方法，自20世紀80年代起由美國Elandt-Johnson教授提出并廣為使用[8，17]。本研究詳細闡述了該模型的方法學原理并用于中國人群壽命表的推算。結果顯示采用Elandt-Johnson模型推算出的年齡別死亡率和生存人數都與真實指標值擬合程度較好。同時推算出的壽命表計算出的預期壽命與實際完全壽命表計算出的預期壽命非常接近。依據壽命表中的年齡組死亡概率，可計算出分年齡、性別和時期的期望生存概率，而期望生存概率是計算人群相對生存率的關鍵指標之一。精確的完全壽命表信息可協助提供特定人群中的期望生存概率，在計算人群癌癥相對生存率中，期望生存概率作為分母調整人群背景死亡概率。在計算我國2003-2015年人群癌癥相對生存率時，由于腫瘤登記地區上報的均為簡略壽命表數據，本研究團隊[4，18]即采用Elandt-Johnson模型法推算出每個腫瘤登記地區分年齡、性別和年份的完全壽命表，后續用于癌癥相對生存率計算。國際癌癥生存分析團隊CONCORD[16]、歐洲人群癌癥生存分析研究協作組EUROCARE[3]也都采用這一方法推算出完全壽命表。有研究表明[19]，針對完全壽命表的推算，Elandt-Johnson模型法較其他完全壽命表推算法推導20～99歲年齡段人口的完全壽命表效果最好。本研究通過實例驗證Elandt-Johnson模型法可以將簡略壽命表推算出較為準確的完全壽命表。