限制空間氮氣置換過程分析與優化

鄭震宇，鄧佳佳，譚金元，盧金樹，薛大文

(浙江海洋大學 港航與交通運輸工程學院，浙江 舟山 316022)

0 引 言

當今世界環境惡劣、污染嚴重，而天然氣因具有燃燒高效、安全環保等優點被大量使用。由于LNG的產地和需求地不匹配，在兩者間需要有運輸環節。運輸時，不可避免地會遇到新液艙或檢修后的液艙，這就需要對液艙進行氣體置換。置換的目標是將液艙內氧氣質量分數降至低于2%，以防止LNG首次進入儲罐時與空氣混合引起爆炸[1]。置換氣體通常采用惰性氣體，常見的惰性氣體有二氧化碳、水蒸氣和氮氣，其中氮氣是較主要的惰性氣體，應用廣泛，不僅適用于各種溫度，而且對管道與裝置的要求也沒有前兩種氣體苛刻，是工業生產中較為理想的惰性氣體[2]。由于置換過程都是在液艙中進行的，因此，研究限制空間內的氣體置換作業過程有利于優化液艙的氣體置換設計方案，具有很大的工程意義。

常用的氣體置換方法主要包括：混合置換、無混合置換、真空置換和加壓置換等4 種置換方式[3-4]。混合置換(又稱為推移式置換)以其易于實現、工作效率高的優點被廣泛采用。黃光容等[5]發現增加富氮氣體流量、提高富氮氣體中氮氣的含量可縮短惰化時間。KURLE等[6]建立了一個飛機燃油箱惰化系統，結果表明，在相同的操作條件下，當惰性氣體流量增加時，所需惰化時間減少。王志偉[7]對燃油箱惰化過程進行研究，發現完成惰化所需氮氣氣體量與進氣方式和載油率有關。宋洋[8]經研究得出氣體入口速度越快，液貨艙惰化速度越快。然而，這些研究很少提及達到推移式置換條件時所需的進口面積、形狀和流速帶來的影響。為此，本文采用CFD數值仿真方法，建立二維模型，通過改變進氣口徑大小和進氣速度，對長為10 m、寬為2 m的限制空間進行氣體置換數值模擬，探究進口面積、形狀和流速對推移式置換的影響。

1 模型

1.1 物理模型

某LNG液艙簡化圖如圖1所示，該液艙長38 m、寬50 m、高10 m[9]。在液艙頂部設有一根水平的進氣管，進氣管上每隔相同距離設有氣孔。在進行液艙惰化時，氮氣從氣孔自上而下噴入，整個液艙中間部分可近似簡化為由無數個含有氣孔的矩形連接而成，相鄰矩形的結構、流場相似，可忽略矩形間的影響。取其中一個矩形進行研究，如圖2所示。為便于研究，簡化后的限制空間長為10 m、寬為2 m。

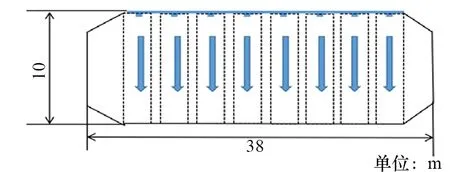
圖1 LNG液艙物理模型

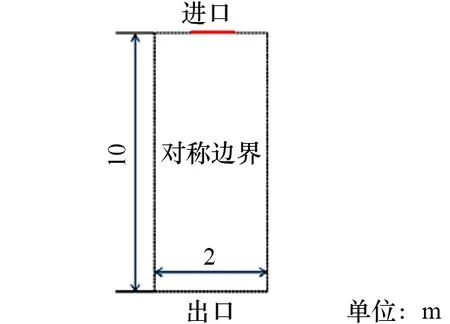
圖2 模型簡化

初始時，液艙內部充滿溫度為300 K，環境壓力為0 Pa的空氣。充入純氮氣進行置換，通入氮氣溫度為300 K。置換的目標是使空間內氧氣質量分數低于2%(為便于研究，忽略空氣中其他稀有氣體)。氮氣及氧氣的物性參數如表1所示。

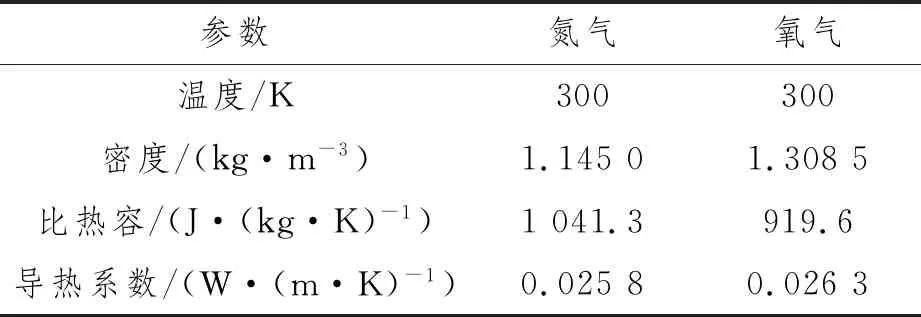
表1 氮氣及氧氣物性參數

1.2 數學模型

由于實際置換過程較為復雜，現作出如下簡化：

(1)實驗艙為絕熱系統，暫不考慮系統的熱耦合。

(2)不考慮限制空間內的泄漏情況，并將限制空間內空氣的成分進行簡化：空氣由21%(體積分數)的氧氣和79%(體積分數)的氮氣組成。

(3)在氣體置換過程中，所需控制方程主要包括質量方程、動量方程、組分控制方程和標準k-ε湍流模型[10]。

1.3 模型設置

利用Gambit 2.4劃分網格，其中限制空間內流體區域設置為流體(Fluid)，網格尺寸為12 mm，Gambit劃分網格數量為1.25×105個。

利用Fluent 15.0進行模擬，選擇2D計算器。模型設置選擇能量方程、標準k-ε湍流模型。選擇重力場，x方向重力加速度的數值為9.81 m2/s。

設置邊界條件和區域條件。將置換氣體進口設置為速度進口，組分為純氮氣，出口設置為壓力出口，對稱邊界條件。在Solution Methods中，壓力速度耦合選擇SIMPLE。在Solution Controls中，壓力、密度分別取0.3 Pa、1 g/cm3，Momentum、Turbulent Kinetic Energy、Turbulent Viscosity、Energy分別取0.7 kg·m/s、0.8 m2/s2、1 Pa·s、1 J。

對全區域進行初始化，其中速度為0 m/s,壓力為0 Pa，溫度為300 K，氧氣體積分數為21%。不設置臨界收斂值，每個時間步長為0.001 s，共計算50 000步，每時間步迭代20次。

2 模型驗證

2.1 計算模型驗證

對實驗艙[11]的氣體置換過程進行模擬，通過對比模擬結果與試驗結果驗證模型的準確性。實驗艙為矩形，長為2.20 m，寬為0.92 m，高為1.22 m。進氣口采用速度入口，出氣口采用壓力出口。在計算過程中，監測艙內氧氣平均質量分數值，將其與試驗結果進行對比，結果如圖3所示，從圖中可以看出計算結果與試驗結果吻合較好。

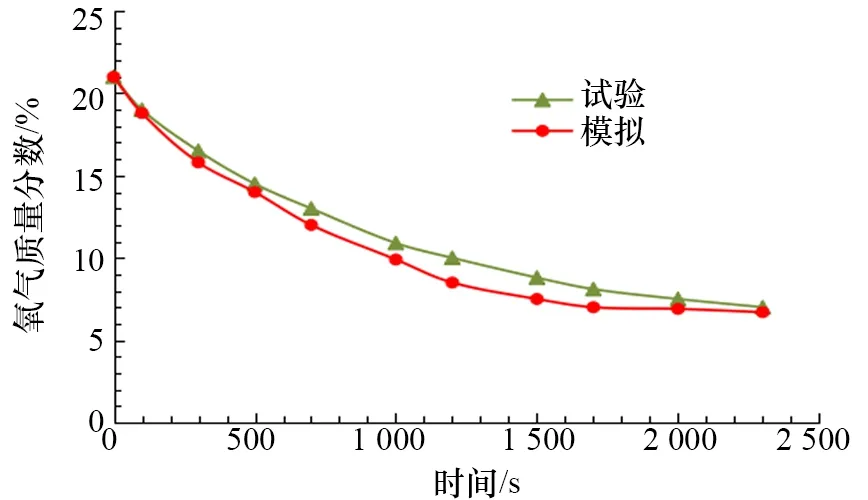
圖3 計算結果與試驗結果對比

2.2 網格無關性驗證

理想的氣體置換氧氣質量分數云圖如圖4所示，云圖大致可分為3層。在進行氣體置換過程中，氮氣和空氣不可避免地會發生氣體擴散，為清晰表達置換效率，理清對流和擴散兩種機理在置換過程中的作用，取氧氣質量分數為10.5%(空氣和純氮氣含氧量中間值)等值面代表對流推移置換效率，入口到該面的體積與實際充入氮氣量一致，進一步取氧氣質量分數2.0%等值面(置換目標)及其關于10.5%等值面的對稱面即氧氣質量分數19.0%等值面，2.0%與19.0%質量分數等值面之間的距離(厚度)代表擴散帶來的影響。

圖4 氧氣質量分數等值面示例

數值模擬計算的基本原理是將計算域離散成多個控制體，并積分得到代數方程，迭代計算得到數值解。采用CFD軟件對限制空間的模型進行建模并劃分網格，進氣時間為3 s。經過網格無關性驗證，網格數量對計算結果影響很小，為減少計算誤差，取均方根σ的誤差率在2%以內，計算結果如表2所示。

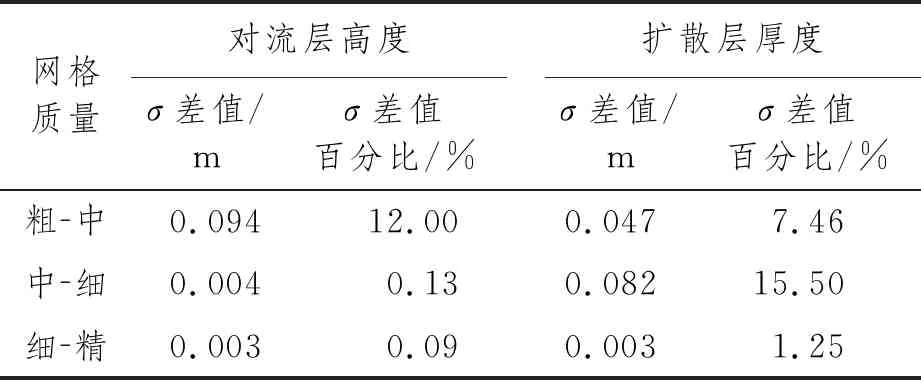
表2 3 s內網格數量敏感性分析

表2中：0.8萬網格代表網格質量為“粗”；3萬網格代表網格質量為“中”；12萬網格代表網格質量為“細”；50萬網格代表網格質量為“精”。綜合考慮計算經濟性和計算準確性，取網格數量為126 246(12萬)個用于計算。

2.3 時間步長敏感度分析

時間步長是指前后兩個時間點之間的差值。在模擬系統的時間響應時往往需設定時間步長，時間步長的大小一般取決于系統屬性和模型的目的。由于對流層高度變化都很小(幾乎沒有改變)，因此為了更直觀地比較，在時間步長分析中只分析擴散帶厚度的變化。3種不同時間步長計算結果如圖5和表3所示。為減少運算量、節約計算資源，時間步長取0.001 0 s。

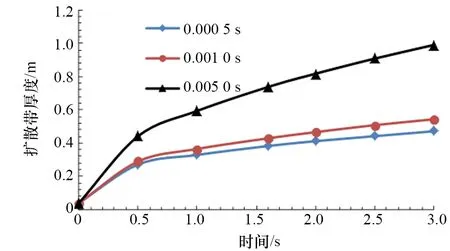
圖5 時間步長敏感度分析結果對比

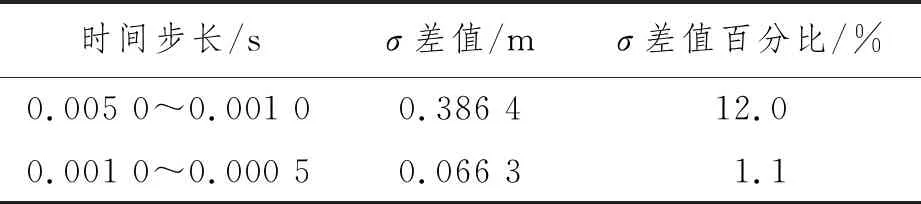
表3 3 s內時間步長敏感度分析

3 氣體置換模擬及機理分析

3.1 無量綱參數

為更好地顯示不同速度下置換所需的氮氣體積，引入無量綱時間τ，其定義為

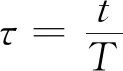
(1)

式中:t為原始時間，s；T為周期，即充入氮氣體積等于置換空間體積所需的時間，s。

當τ=1時，代表充入氮氣體積等于限制空間體積；當τ>1時，代表充入氮氣體積大于限制空間體積。

3.2 基準方案結果分析

取口徑大小占限制空間寬比例為20%、30%和40%，初始速度暫設定為2 m/s。選取無量綱時間τ為0.3、0.6和0.9的氧氣質量分數云圖進行對比分析，如表4所示。

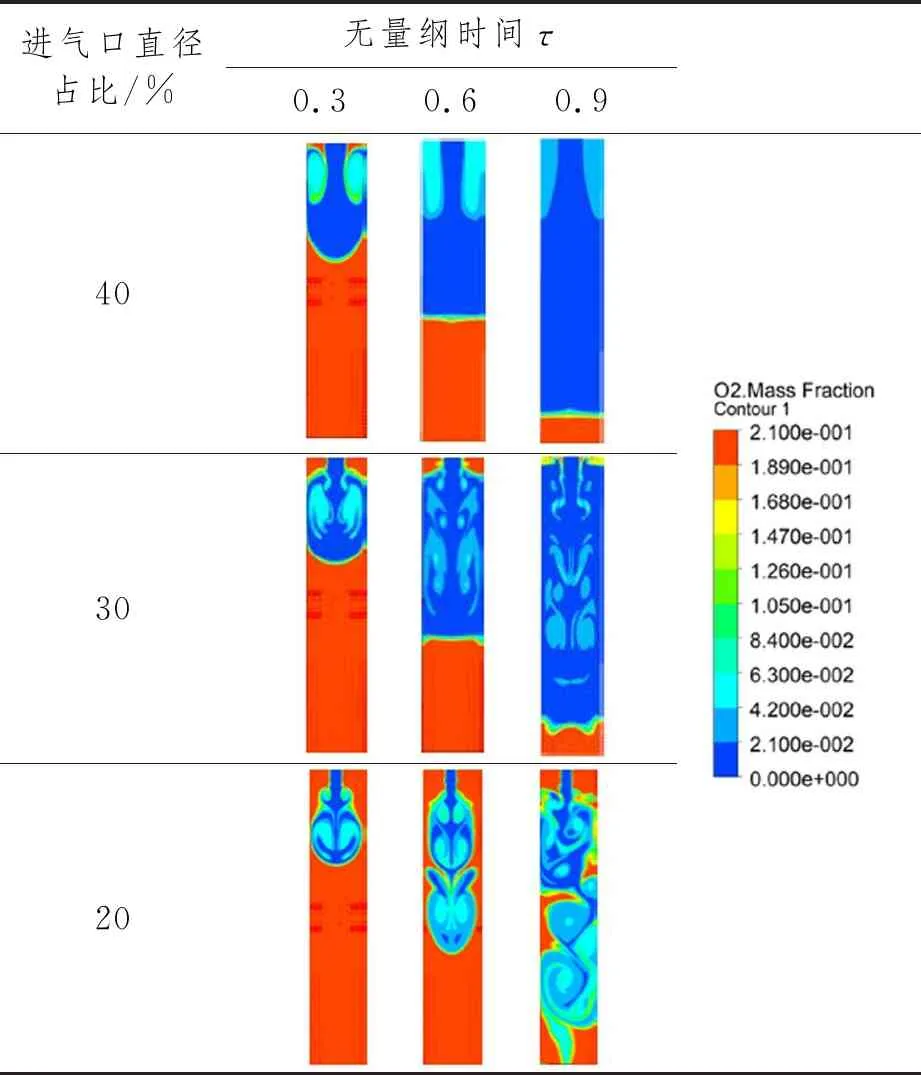
表4 不同進氣口直徑下氧氣質量分數分布

判斷推移式置換的標準為氧氣質量分數各等值面隨時間的變化平穩移動。當進氣口大小占比為20%時，限制空間氧氣云圖顯示內部氣體氧氣質量分數分布雜亂無章，充入氮氣與空氣明顯發生混合，不符合推移式置換要求。在進氣口大小占比為30%～40%時，氧氣質量分數云圖顯示對流與擴散分界線明顯，說明增大進氣口直徑容易實現推移式置換。

進氣口直徑占比為20%、30%和40%的對流層與擴散層變化如圖6所示。20%工況對流層隨著時間的推移變化較小，始終維持在空間頂部，無法形成平整的質量分數等值面。相對來說，進氣口直徑占比為30%和40%的對流層和擴散層運動規律明顯。然而在實際工程應用中，進氣口的直徑都較小，因此考慮保持小進氣口，并以層層擴大的進氣方式完成限制空間的氣體置換。

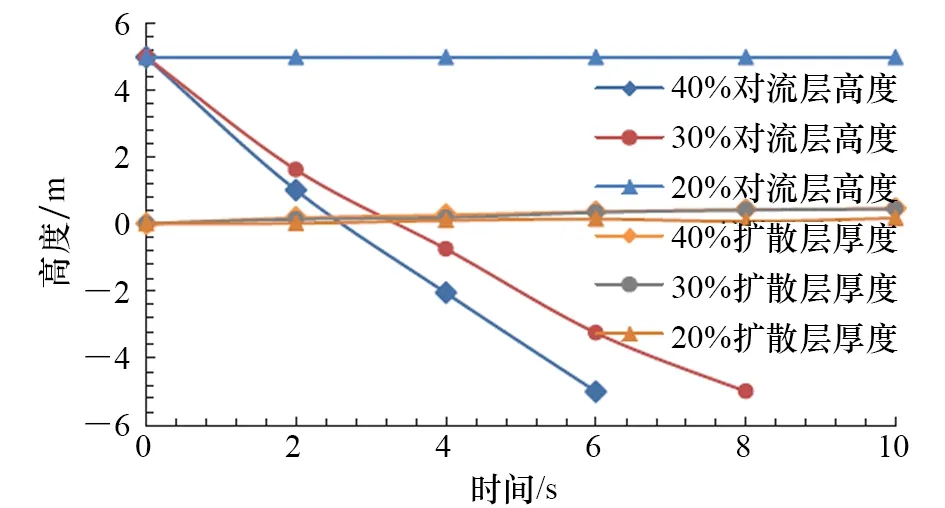
圖6 氧氣質量分數隨時間變化的坐標高度

4 優化方案及機理分析

4.1 優化結果

在限制空間上方加裝2個矩形嵌套，進氣口占矩形寬的一定比例，長度為1 m，進氣方式為上進下出，進氣速度初步設為2 m/s,其余條件不變。當進氣口直徑占比為20%時，優化效果明顯。優化前后氧氣質量分數云圖如表5所示。

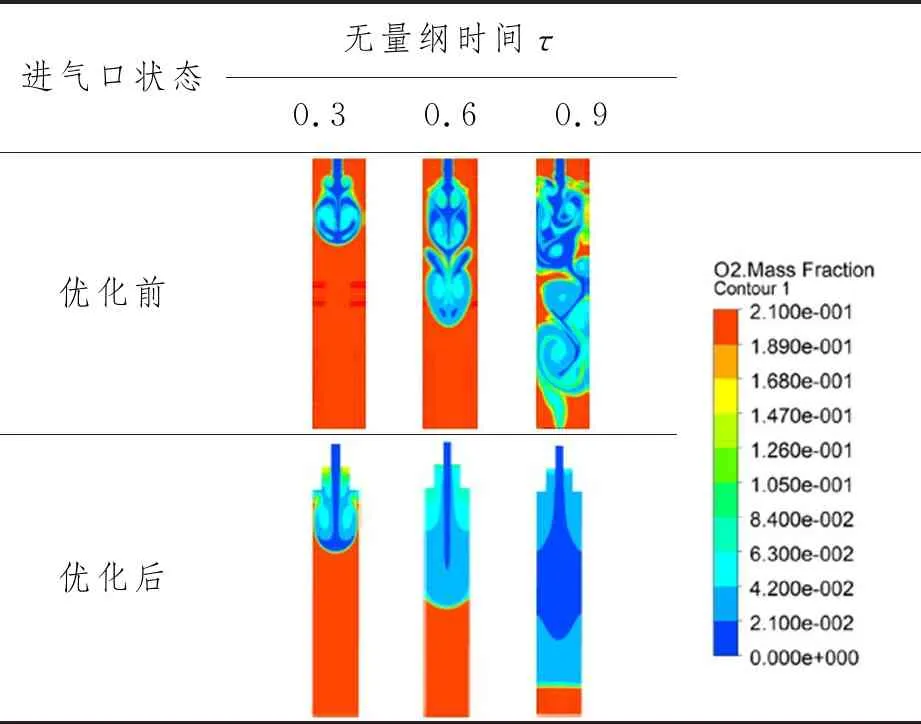
表5 優化前后氧氣質量分數分布

從表5可知：優化后，20%入口比例工況基本實現推移式置換，優化效果明顯。由于空間為對稱邊界，選取中線靠右側半個計算區域進行優化前后速度分布對比，以分析優化前后置換效率改變的原因。圖7所示為距進氣口0.5 m、1.0 m、2.0 m和3.0 m的平面位置。無量綱時間為0.3、0.6和0.9時的平面速度標準偏差對比如圖8所示。由圖8可知：優化后各平面的速度標準偏差均有所降低，且0.5 m平面速度標準偏差最大，最具代表性，因此后續均選取0.5 m平面進行進一步分析。

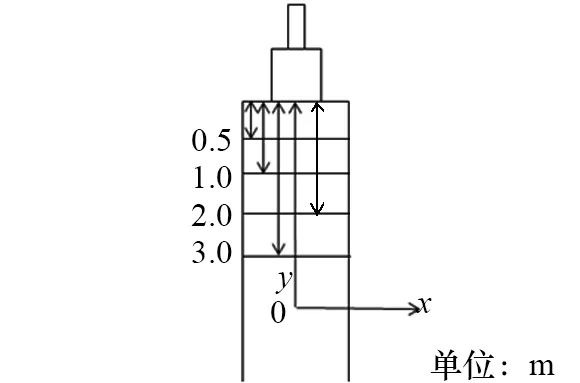
圖7 不同平面位置

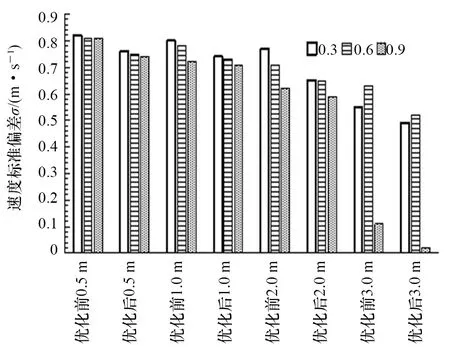
圖8 優化前后距進氣口不同位置速度標準偏差對比

4.2 優化機理分析

圖9為優化前后距進口0.5 m平面的速度分布對比圖。從圖9可以看出：不同時刻優化后，0.5 m平面速度分布曲線比初始方案更平坦，整體呈“乁”字形；優化后速度上拐點提前約50%，說明同一位置優化后速度下降更快；優化后無明顯的速度下拐點，中間有段區域優化后速度比優化前大，但整體曲線后半段較為平坦，說明優化后整個平面速度場更均勻，有利于形成推移式置換。圖10為對應速度分布標準偏差對比，橫坐標為優化前后無量綱時間0.3、0.6和0.9時刻。從圖10可以看出，優化后0.5 m平面速度分布標準偏差平均降低8.5%，最高降低10.8%，最低降低6.6%。

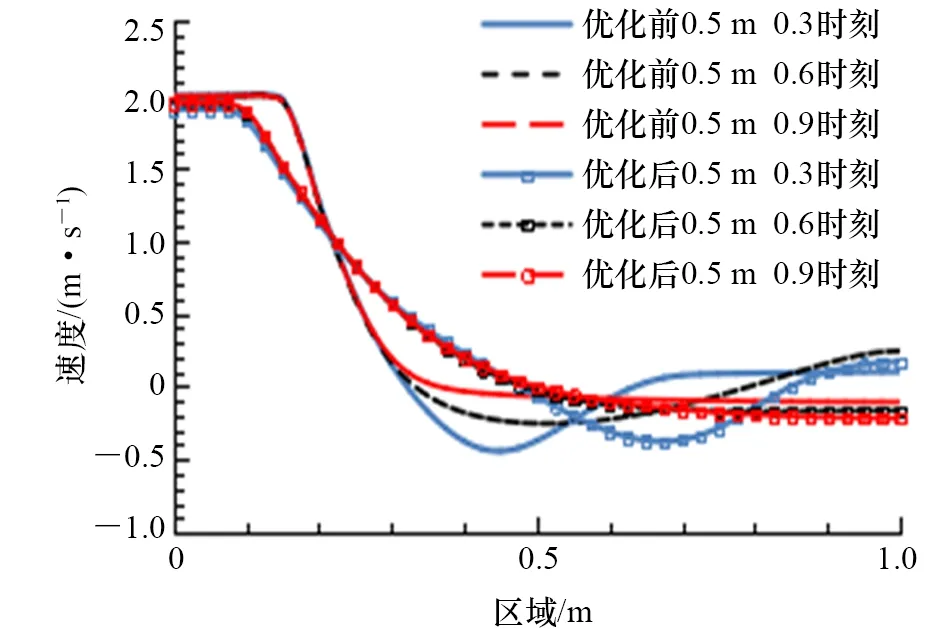
圖9 優化前后距進口0.5 m處速度分布對比

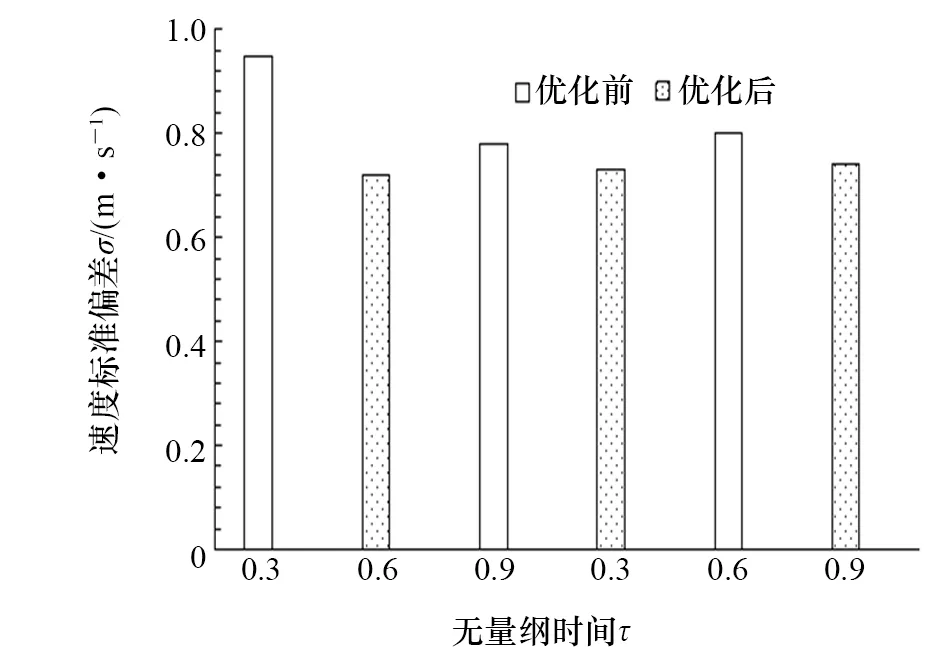
圖10 優化前后距進口0.5 m處速度標準偏差對比

圖11和圖12是不同時刻優化前后0.5 m平面氧氣質量分數分布曲線和氧氣質量分數分布標準偏差對比圖。從圖11可以看出，優化后0.5 m平面質量分數分布明顯較優化前均勻，優化后氧氣質量分數拐點同樣提前約50%，說明同一位置優化后氧氣質量分數提前升高。在曲線后半段，優化后質量分數小于優化前并且曲線較平坦，說明此時整個平面質量分數梯度小，平面質量分數較為均勻。從圖12可以看出，優化后0.5 m平面氧氣質量分數分布標準偏差平均降低124.3%，最高降低210.2%，最低降低44%。

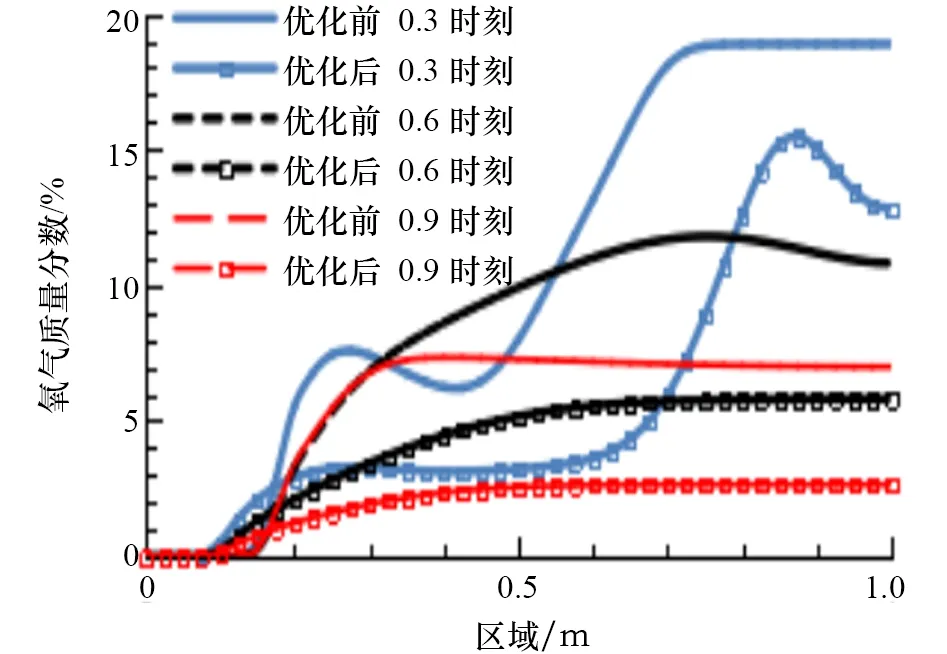
圖11 氧氣質量分數分布

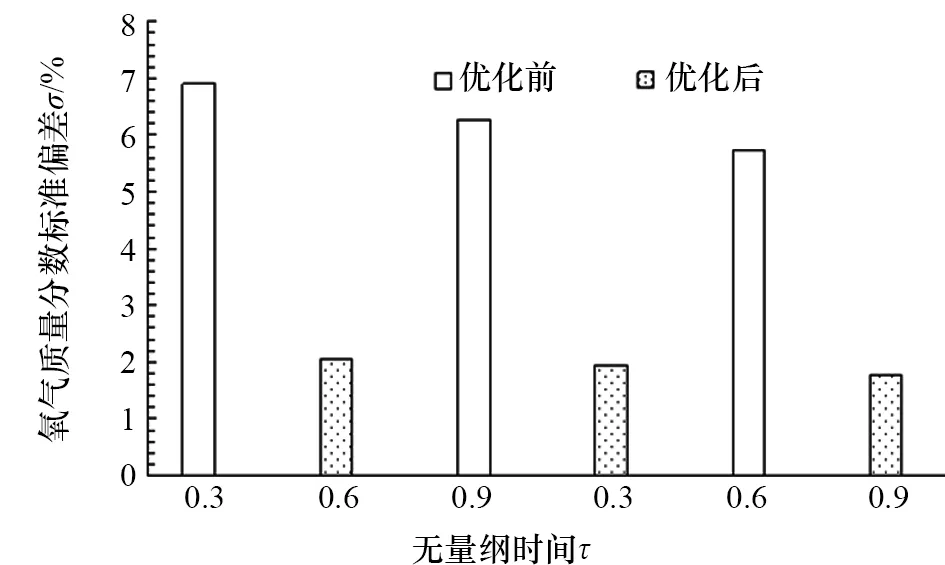
圖12 氧氣質量分數標準偏差

4.3 優化結果分析

優化方案與原始方案完成置換所需的無量綱時間對比如表6所示。在不同速度時，優化方案無量綱時間均比基準方案小，差異較大的20%無量綱時間相差在1.58%～11.21%，說明方案經過優化后明顯節省氮氣量，具有一定的工程意義。

表6 優化前后不同進氣速度無量綱時間對比

在優化方案下，不同進氣速度氧氣質量分數分布如表7所示。當速度增大時，空間內易形成漩渦，導致耗氮量增大，說明進氣速度低時經濟性好。

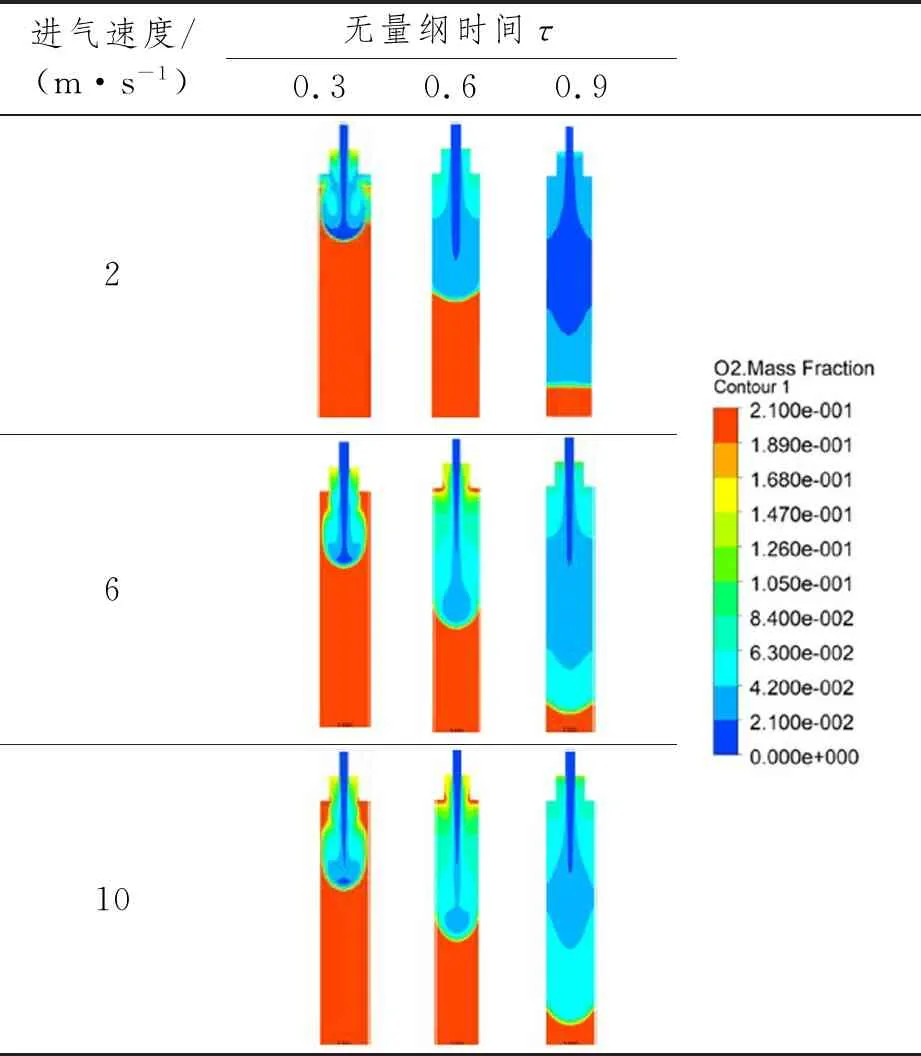
表7 優化方案下不同進氣速度氧氣質量分數分布

在實際置換過程中，最理想的方案是以最少的耗氮量和最短的時間完成置換。優化方案實際完成置換所需時間如表8所示，當進氣速度為2 m/s時，優化效果最明顯，可節省17%的時間。因此，優化方案可節省實際工程時間，具有可行性。

表8 優化前后不同進氣速度實際置換時間對比

5 結 論

基于CFD方法對限制空間氮氣置換過程進行數值模擬，分析不同進氣方式對置換效果帶來的影響，提出相關優化建議。得到結論如下：

(1)基于CFD方法計算限制空間內的平均氧氣質量分數與文獻試驗中的數據吻合較好，說明該模型能夠較準確地模擬限制空間內氮氣置換過程。

(2)進氣口越大越容易實現推移式置換；優化方案與原始方案相比可減少約1.58%～11.21%的氮氣量，最多可縮短17%的置換時間，具有更好的經濟性。

(3)優化方案中減慢進氣速度可減少耗氮量，但會延長置換時間。因此，根據目標不同可選擇不同的進氣速度。

根據模擬計算結果，對置換過程各參數進行分析，為提升置換作業過程的經濟性和安全性，提出如下建議：

(1)在實際置換作業過程中，將氮氣進氣口形狀改裝成矩形嵌套可減少置換所需的氮氣量。

(2)雖然適當提升進氣速度可減少置換時間，但是流速太高會使管道內的焊渣等可移動物體在高速氣流攜帶下運動，易與管道碰撞，產生電火花[12]，因此進氣流速控制在2～5 m/s為宜。