環(huán)形智能加工系統(tǒng)中RGV的動態(tài)調(diào)度策略

袁夢婷

摘要：基于MDP理論，將“RGV執(zhí)行并完成任務所需時間”構(gòu)建為動態(tài)優(yōu)先級，引入隨機變量“CNC發(fā)生故障和排除故障的時間”，結(jié)合RGV、CNC、物料的狀態(tài)變化情況，建立基于MDP理論的狀態(tài)轉(zhuǎn)移模型。并在數(shù)值迭代算法的基礎上設計了MDP迭代尋優(yōu)算法對三組系統(tǒng)進行求解，從而得到一道工序物料加工過程中，CNC有1%的概率發(fā)生故障的情形下環(huán)形智能加工系統(tǒng)在未知動態(tài)環(huán)境下的最優(yōu)調(diào)度策略。

Abstract： Basing on the MDP theory， we construct the time of RGV to execute and complete the task as the dynamic priority， and introduce two random variables， the time when the CNC is faulty and the fault is removed. At the meanwhile， combining with the state changes of RGV， CNC and materials， we establish a state transition model based on MDP theory. Then， based on the numerical iterative algorithm， the MDP iterative optimization algorithm is designed to solve the three groups of systems， so that the optimal scheduling strategy of the intelligent processing system in an unknown dynamic environment during the processing of a process material with a 1% probability of failure in the CNC is obtained.

關鍵詞：MDP理論;動態(tài)優(yōu)先級;迭代尋優(yōu)算法;動態(tài)調(diào)度最優(yōu)策略

Key words： MDP theory;dynamic priority;iterative optimization algorithm;dynamic scheduling optimal strategy

中圖分類號：TP273 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1006-4311（2019）27-0043-03

0 ?引言

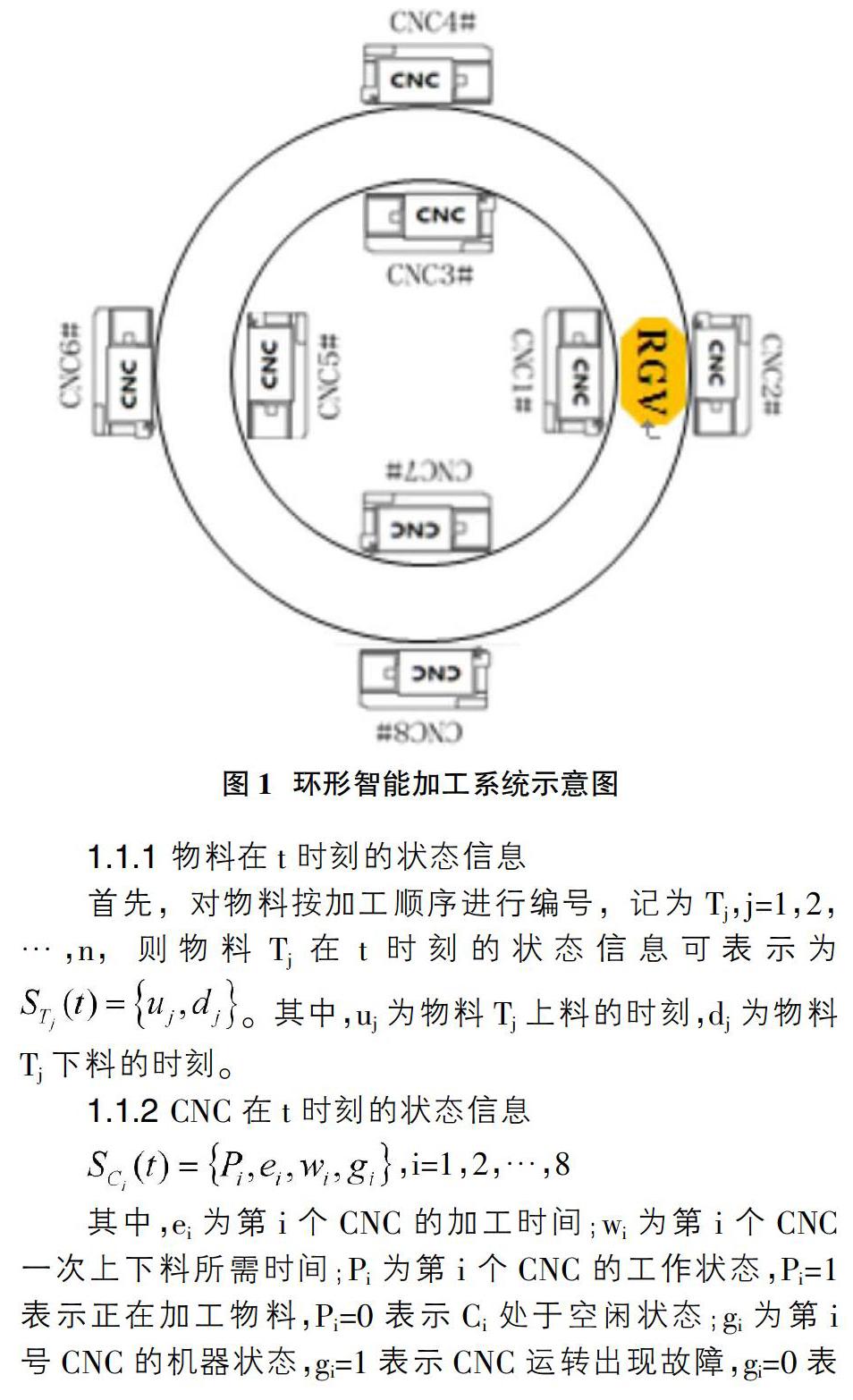
隨著當今世界科學技術的蓬勃發(fā)展，現(xiàn)代物流觀念漸漸深入人心。為解決龐雜的物流問題，自動化物流系統(tǒng)開始興起，然而如何合理地設計智能加工系統(tǒng)的調(diào)度策略從而提高效率是自動化系統(tǒng)的核心。如今，已有大量研究者致力于解決RGV的動態(tài)調(diào)度策略。張桂琴等[1]設計了RGV的智能調(diào)度算法和避碰防撞算法，解決了2輛RGV的相向碰撞和同向追尾問題;沈艷等[2]針對網(wǎng)絡控制系統(tǒng)中采樣周期時變不確定性對控制和運行性能的影響，提出了基于反饋控制原理和預測機理的動態(tài)調(diào)度策略;查振元等[3]著重分析了RGV的應用。這些雖然給出了很多解決各種情況下的調(diào)度策略，但是沒有對實際加工情境進行分析。因此本文主要以圖1所示的環(huán)形智能加工系統(tǒng)為例（RGV固定逆時針移動），研究一道工序物料加工過程中，CNC有1%的概率發(fā)生故障的情形下環(huán)形智能加工系統(tǒng)在未知動態(tài)環(huán)境下的最優(yōu)調(diào)度策略。

1 ?基于MDP理論的狀態(tài)轉(zhuǎn)移模型

1.1 狀態(tài)分析

本文將系統(tǒng)端視為觀察者，RGV視為決策者，以RGV執(zhí)行并完成任務所需時間為動態(tài)優(yōu)先級，時間越短優(yōu)先級越高為決策依據(jù)，使RGV做出決策并執(zhí)行任務，從而使各CNC的運轉(zhuǎn)狀態(tài)發(fā)生改變。并以RGV位于CNC1#和CNC2#正中間，所有CNC都處于空閑狀態(tài)為初始狀態(tài)，分別對物料、CNC及RGV的狀態(tài)進行分析。

1.1.1 物料在t時刻的狀態(tài)信息

1.1.2 CNC在t時刻的狀態(tài)信息

由于在加工過程中，我們無法判斷CNC何時出現(xiàn)故障，因此對它設定隨機變量ε1，其范圍為0到對應CNC加工一個物料所需時間，使CNC在加工過程中的某個時刻出現(xiàn)概率為1%的故障，無法正常加工。同理，由于故障排除時間在10～20分鐘內(nèi)，我們無法確定每次故障排除的準確時間，因此再設定隨機變量ε2，其范圍為600s至1200s，使CNC發(fā)生故障后的10～20分鐘的某個時刻恢復正常運轉(zhuǎn)狀態(tài)。

1.2 建立模型

1.2.1 動態(tài)優(yōu)先級的構(gòu)建

為提高系統(tǒng)工作的效率，本文建立RGV執(zhí)行并完成任務所需時間T為其決策的動態(tài)優(yōu)先級，RGV將在發(fā)出信號的CNC數(shù)量大于1時根據(jù)動態(tài)優(yōu)先級進行判斷，并做出決策，T越小，優(yōu)先級越高，任務越先被執(zhí)行。

1.2.2 狀態(tài)轉(zhuǎn)移模型

1.3 模型求解

1.3.1 模型的求解算法——MDP迭代尋優(yōu)算法

由于智能加工系統(tǒng)處于一個動態(tài)變化的過程，因此每一次決策的任務分配都會影響到整個系統(tǒng)的總體效率，為了滿足加工系統(tǒng)動態(tài)任務分配的快速性要求，根據(jù)MDP最優(yōu)策略的存在性判定定理[5]，我們所建立的基于MDP理論的狀態(tài)轉(zhuǎn)移模型一定存在最優(yōu)策略，可用數(shù)值迭代算法進行求解。結(jié)合本文實際情況，我們在數(shù)值迭代算法的基礎上進行優(yōu)化，設計了MDP迭代尋優(yōu)算法。此算法在迭代的過程中可計算出在可能發(fā)生故障的情況下，RGV每次分配任務后整個系統(tǒng)的狀態(tài)，最終求解出最優(yōu)動態(tài)調(diào)度策略。

1.3.2 求解結(jié)果

考慮CNC可能會發(fā)生故障的情況，依據(jù)基于MDP理論的狀態(tài)轉(zhuǎn)移模型，結(jié)合MDP迭代尋優(yōu)算法，利用相關系統(tǒng)作業(yè)參數(shù)，我們通過MATLAB軟件，求解得到一道工序物料在有故障情形下RGV的最優(yōu)動態(tài)調(diào)度策略。（表1）

1.3.3 敏感性分析

由于CNC發(fā)生故障情形中存在隨機變量，使得結(jié)果在每次算法的運行后都不一樣，因此本節(jié)主要分析本文中基于MDP理論的狀態(tài)轉(zhuǎn)移模型的敏感性。又由于不同故障數(shù)對結(jié)果影響大致相同，故在此我們以第1組為例進行具體分析。

給予清洗時間在[-1，1]范圍內(nèi)以0.1為間隔的誤差，運用MATLAB軟件，將結(jié)果繪制成折線圖，從而更清晰得反映結(jié)果的變化，如圖2所示。

觀察圖2可以發(fā)現(xiàn)，參數(shù)的誤差對模型的結(jié)果有一定的影響，但是影響程度較小，即模型的敏感性較低，從而證明了基于MDP理論的狀態(tài)轉(zhuǎn)移模型具有較高的可靠性。

2 ?結(jié)論

對比智能加工系統(tǒng)實際應用情況[3]，可以發(fā)現(xiàn)我們求解得到的結(jié)果具有一定的實際性和正確性，證明了建立的基于MDP理論的狀態(tài)轉(zhuǎn)移模型的實用性及MDP迭代尋優(yōu)算法的有效性。

本文的特色與創(chuàng)新點在于，巧妙地利用了MDP馬爾可夫周期性和連續(xù)性的性質(zhì)，并在此基礎上構(gòu)建動態(tài)優(yōu)先級，建立狀態(tài)轉(zhuǎn)移模型，同時結(jié)合迭代尋優(yōu)算法對問題進行求解。

參考文獻：

[1]張桂琴，張仰森.直線往復式軌道自動導引車智能調(diào)度算法[J].計算機工程，2009，35（15）：176-178，181.

[2]沈艷，郭兵.網(wǎng)絡控制系統(tǒng)變采樣周期智能動態(tài)調(diào)度策略[J].四川大學學報（工程科學版），2010，42（01）：162-167.

[3]查振元，李計星，繩潤濤，張豐華，李昌臣.智能平移軌道導引車的應用[J].機器人技術與應用，2017（05）：42-43.

[4]陳明，周云龍，劉晉飛，靳文瑞.基于MDP的多Agent生產(chǎn)線動態(tài)調(diào)度策略[J].機電一體化，2017，23（11）：15-19，56.

[5]鄭少慧.一類連續(xù)時間平均馬氏決策平穩(wěn)最優(yōu)策略的存在性[J].應用數(shù)學學報，1989（02）：250-256.