地鐵列車最優黏著控制研究

李會子， 郭其一

(同濟大學 電氣工程系， 上海 201804)

在交流傳動地鐵車輛牽引控制中，空轉/滑行保護和黏著利用控制是牽引控制系統的一部分，統稱為黏著利用控制系統。如圖1所示，在線路軌面狀況變化不定的情況下，比如軌面干燥、潮濕、雨雪等外界條件變化時，列車的牽引力不能得到有效利用，黏著利用控制系統的主要作用是通過對電機速度，電機轉矩等信息的采集，分析和處理，綜合得出電機轉矩指令，向電機控制系統發出合適的電機轉矩給定，使得列車能以接近線路當前最大的黏著系數運行，從而獲得最大的黏著利用率。

文獻[1]采用了相位法來間接測量黏著特性曲線斜率，根據線性系統理論，在電機轉矩給定上疊加一定頻率和幅度的正弦測相信號，使黏著利用效率可以達到80%以上，但是疊加信號產生的干擾將會影響電機控制性能[1]。文獻[2]采用組合校正法，通過速度差和加速度與設定閾值比較來判斷列車的運行狀態，從而調節電機的轉矩。但是組合校正法是在檢測到列車發生空轉/滑行之后動作的，黏著利用率較低[2]。文獻[3]將滑模極值搜索算法應用到汽車ABS防抱死剎車系統中，補償車輛轉彎時的側向穩定性，使車輛能夠適應路面黏著系數的變化[3]。

永磁同步牽引系統具有節能環保的優點，針對地鐵列車的最優黏著控制問題，考慮到永磁同步電機軸控技術的不斷推廣與應用。首先搭建了列車單軸動力學模型，設計全維狀態觀測器對軌面黏著系數進行估計，其次采用滑模變結構設計控制器對電機控制轉矩進行調節，從而提高列車的黏著利用率。

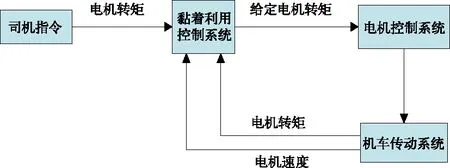
圖1 黏著利用控制系統在傳動控制中的位置

1 列車模型和輪軌黏著特性

1.1 列車單軸動力學建模

地鐵列車的基本配置為6輛車編組，由4輛動車車輛和2輛拖車車輛組成。其中動車車輛裝有動力牽引裝置，車輛轉向架上安裝有牽引電機，由牽引電機將電能轉換為機械能，通過齒輪箱傳動軸傳遞到輪對上，產生列車前進所需要的黏著力。圖2為列車輪軌黏著力牽引示意圖。

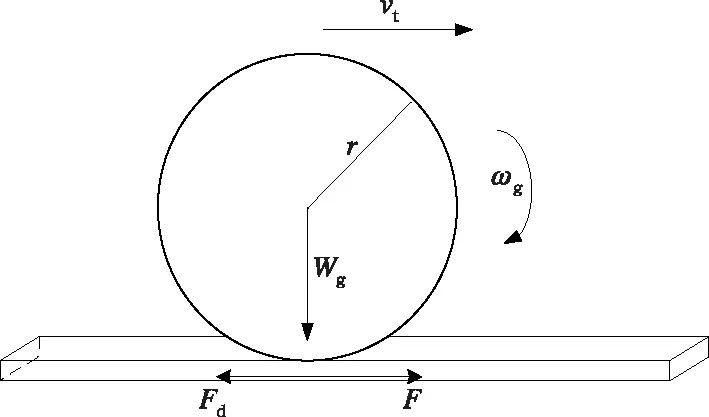
圖2 列車單軸黏著力示意圖

齒輪箱的傳動特性為：

(1)

車輪線速度與角速度之間有如下關系式：

vd=ωd·r

(2)

列車在牽引前進的過程中，車輪線速度與車體速度直線的差值定義為蠕滑速度：

vs=vd-vt

(3)

牽引電機的動態方程為：

(4)

負載轉矩 滿足如下關系式：

(5)

列車運動方程為：

(6)

基本阻力公式為：

Fd=((1.65+0.024 7×vt)×Mm+

(0.78+0.002 8×vt)×Mt+(0.028+0.007 8×

(N-1))×vt2)×9.8/1000

(7)

其中，ωm是牽引電機角速度;ωd是車輪角速度;vd是車輪線速度;vt是車體速度;vs是蠕滑速度;μ(vs)是軌面黏著系數;F是單軸列車模型輪軌之間產生的黏著力;Fd是列車運行的阻力;W是列車單軸軸重;M是整車質量;r是車輪半徑;Rg是齒輪箱的傳動比;Tm是電機電磁轉矩;TL是電機負載轉矩;Jm是歸算到電機側的等效轉動慣量(即車輪和牽引電機轉動慣量歸算后的等效值);B是歸算到電機側的等效黏滯系數(即輪軸和電機軸摩擦黏滯系數歸算后的等效值);Mm是列車動車自重;Mt是列車拖車自重;N是地鐵列車的車輛數。

1.2 黏著特性曲線

軌面黏著系數可以反應輪軌間的接觸情況，大量試驗表明黏著系數與蠕滑速度之間的特性關系可以用式(8)表示：

μ(vs)=c·e-avs-d·e-bvs

(8)

其中a、b、c是軌面條件參數，表1給出了4種不同軌面下條件參數的取值。

不同軌面條件下黏著系數的最優值及該值對應的蠕滑速度計算公式如式(9)～式(10)

(9)

(10)

表1 不同軌面下的計算參數

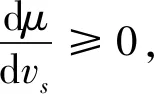
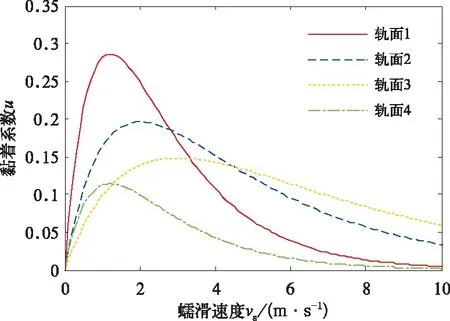
圖3 黏著特性曲線

2 全維觀測器的設計

根據車體的動力學方程可得到狀態空間表達式如式(11)

(11)

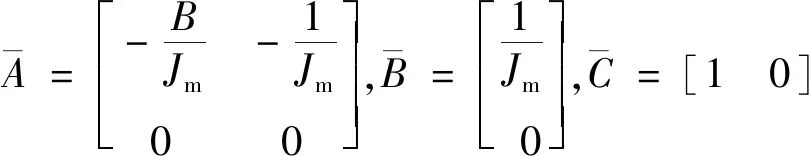
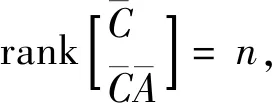
采用極點配置方法設計全維狀態觀測器：

(12)

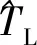
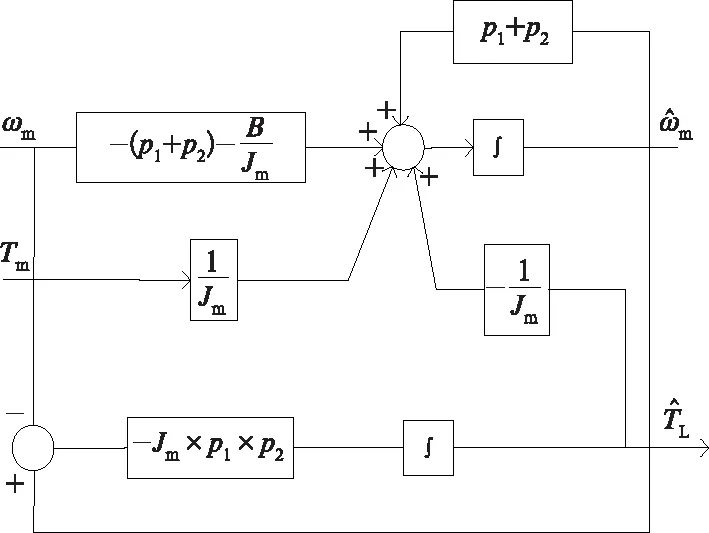
圖4 全維狀態觀測器

因此：

(13)

黏著系數的估計值為：

(14)

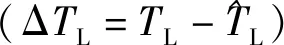
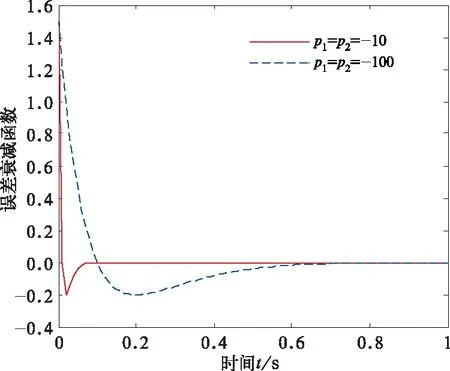
圖5 不同極點下的誤差衰減曲線

3 滑模變結構控制器的設計

3.1 滑模極值搜索最優蠕滑速度

為了提高列車的黏著利用率，黏著利用控制系統采用滑模極值搜索算法搜索出當前軌面下的蠕滑速度最優值，使黏著系數盡可能達到最大。

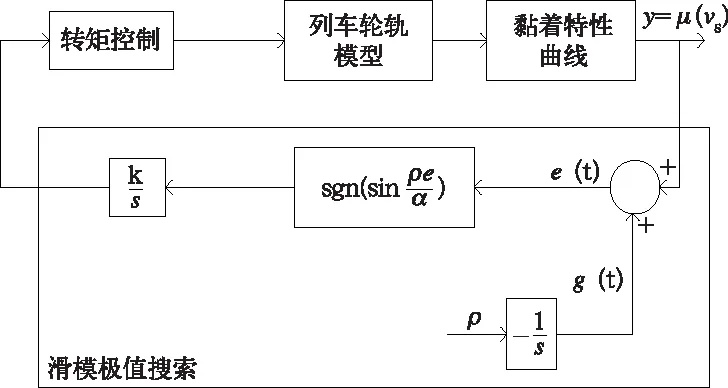
圖6 滑模極值搜索算法原理圖

設切換函數為：

e(t)=y(t)-g(t)

(15)

(16)

選擇最優蠕滑速度觀測值的導數為控制律：

(17)

將式(17)帶入到式(16)中可得：

(18)

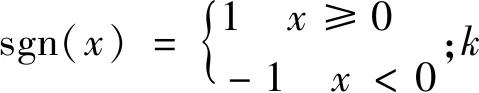
存在一個常數C，滿足：

(19)

那么滑模運動將會發生在e(t)=C的滑模面上。

(1)當e(t)定義域為[(n-1)α,nα]時，

(e(t)-nα)·(e′(t)-nα)=(e(t)-nα)×

(20)

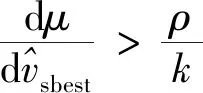
(e(t)-nα)·(e′(t)-nα)<0

(2)當e(t)定義域為[nα，(n+1)α]時，

(e(t)-nα)·(e′(t)-nα)=(e(t)-α)×

(21)

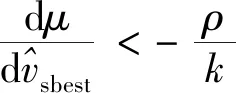
(e(t)-nα)·(e′(t)-nα)<0

3.2 滑模變結構轉矩控制器的設計

通過滑模極值算法跟蹤得到當前軌面條件下的最優蠕滑速度值，需要對電機轉矩進行控制使列車可以以最優蠕滑速度運行，從而最大化的利用軌面的黏著率。由于滑模變結構針對帶有不確定性和外加干擾的系統可以通過設計控制率來實現較強的魯棒控制，因此下面將實現等效控制來實現列車的轉矩控制。

定義滑模面為 ：

s(t)=vs-vsbest

(22)

(23)

當蠕滑速度達到最優蠕滑速度時，則滿足s(t)=0，s′(t)=0。

為使系統可以一直穩定在滑模面上運動，采用等效控制ueq為基礎的形式來設計控制律。

(24)

(25)

(2)當系統不在滑模面上運動時，需要加入一個控制信號來使系統的狀態趨近于滑模面運動，最終穩定在滑模面上。

Tm=u=ueq-q·sgn(s(t))

(26)

將式(25)代入到式(23)中得：

(27)

該控制律使系統最終可以穩定在滑模面上：

(28)

4 仿真與分析

在MATLAB/Simulink中根據控制系統框圖搭建單軸列車傳動過程中的黏著控制系統仿真模型。地鐵列車的仿真參數如表2所示。

表2 地鐵列車參數(上海地鐵13號線)

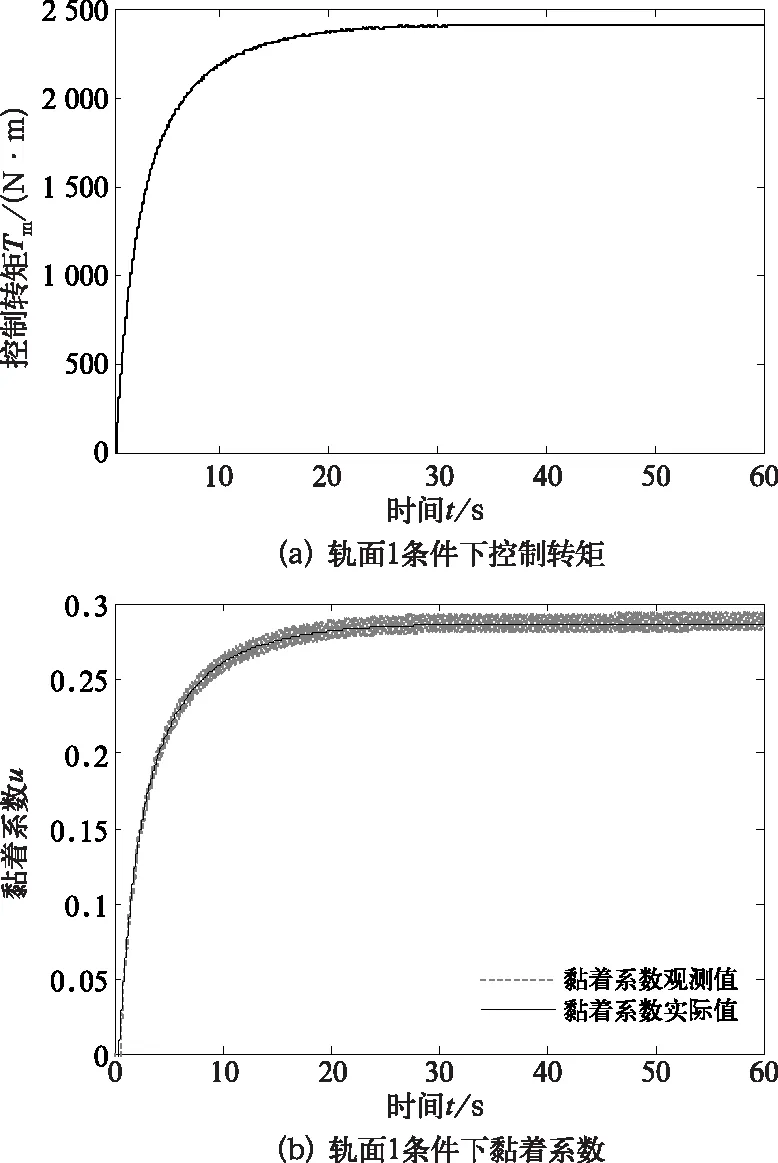
圖7 軌面1條件下黏著控制仿真結果

從圖7(a)中可以看出，當列車運行在軌面1上啟動并加速的過程中，如果司機給定轉矩指令為3 000 N·m，列車在20 s時控制轉矩Tm可以達到2 400 N。圖7(b)中此時黏著系數達到0.28，隨后穩定在0.28附近，充分利用了黏著率。

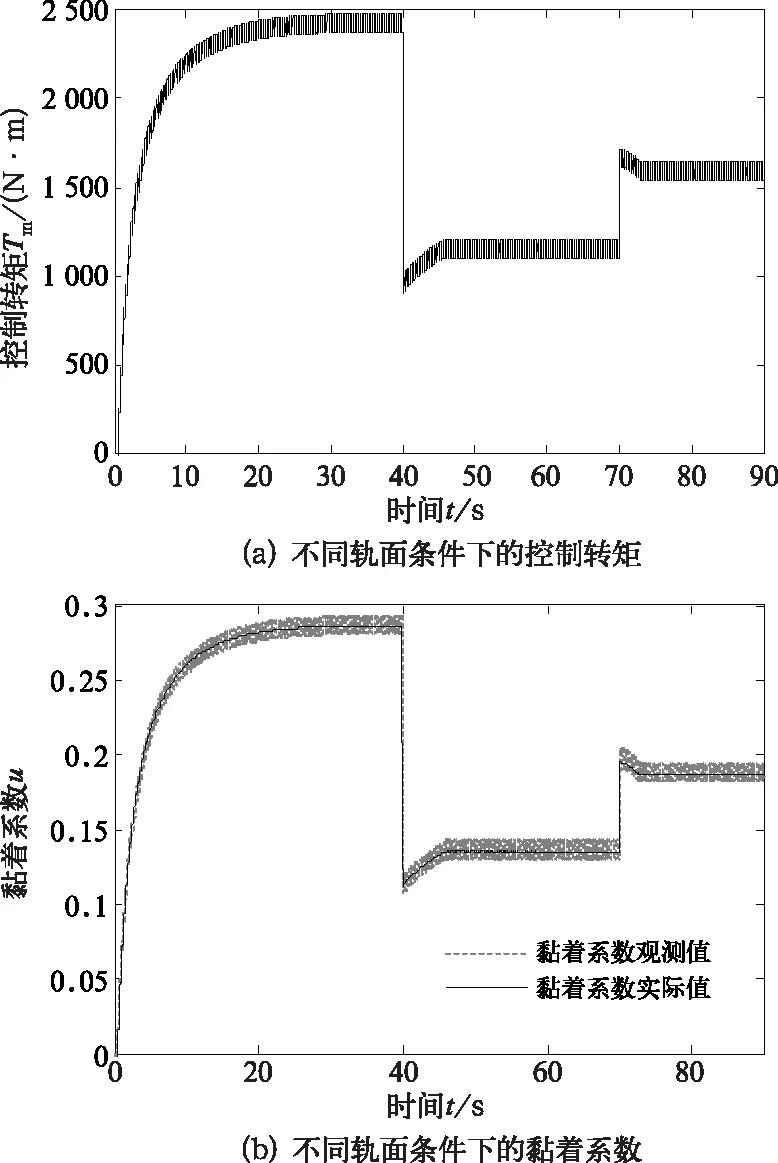
圖8 不同軌面條件下黏著控制仿真結果

圖8中實現的是在不同軌面條件下進行切換的過程，整個仿真時間為90 s。在0～40 s，列車運行在軌面1的條件下，控制轉矩和黏著系數的仿真結果和圖7所示相同。在40～70 s，列車切換到軌面3運行，由于黏著系數突然下降，因此電機控制轉矩在段時間內快速調整，減小并穩定在1 200 N ，黏著系數大概在0.14。避免空轉滑行的同時充分利用了黏著率。在70～90 s的時間段，切換到軌面2運行，黏著系數增加，因此電機控制轉矩調整到1 600 N ，此時黏著系數穩定在0.19左右。總體來看，控制轉矩和黏著系數隨軌面變化情況一致，在不同軌面下進行切換時可以快速調整到最優蠕滑速度下運行，提高黏著利用率。

5 結 論

設計了滑模變結構控制器，用來對地鐵列車的電機轉矩進行控制調整。并基于MATLAB/Simulink對地鐵列車的單軸牽引模型進行仿真，對不同軌面條件下的最優蠕滑速度進行搜索，提高了黏著利用率，實現了最優黏著控制。最近一段時期，基于永磁同步電機的軸控技術在推廣應用，以及車載計算機的性能不斷提升，該控制技術可以付諸實踐與應用。