用思維導圖發現簡便運算的秘密

□施樂旺

小朋友，你喜歡簡便運算嗎？有的同學會覺得簡便運算非常簡單，有的同學會苦惱怎么看都沒看出哪里可以簡便。別苦惱，我們用思維導圖來個逆向思維活動，讓你大開腦洞發現簡便運算的秘密。

首先，我們想一想，是不是所有的混合運算都可以進行簡便運算？顯然不是。那什么樣的算式可以簡便運算呢？不著急，我們以100 為例，想一想：哪兩個數相加的和是100？

75 加25 的和是100，32 加68 的和是100……其實你想到的“75＋25”“32＋68”就“潛伏”在簡便運算的算式里，請看：它可能“潛伏”在75＋38＋25 里，聰明的你是不是馬上想到了用加法交換律就可以識破偽裝，輕松計算：75＋38＋25＝75＋25＋38＝100＋38＝138；它還可能“潛伏”在38＋75＋25 里，這時只需加法結合律出場即可：38＋75＋25＝38＋（75＋25）＝38＋100＝138；它還可能“潛伏”在38×75＋38×25里，這時只需乘法分配律出場即可：38×75＋38×25＝38×（75＋25）＝38×100＝3800。

兩個數相加的和藏在簡便運算里的情況還有一種藏得更深，如36×99＋36，它表示的是99 個36 加1 個36，所以36×99＋36＝36×（99＋1）＝36×100＝3600。

只有兩個數相加的和是100 嗎？它們又會“潛伏”在什么樣的算式里呢？我們用思維導圖記錄下來：

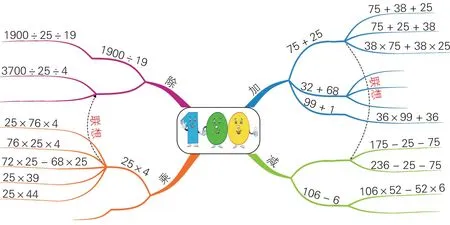
上面舉的例子只是一部分，但已經涵蓋了加法交換律、加法結合律、乘法交換律、乘法結合律、乘法分配律，還有連減的性質和連除的性質。這樣的例子還有很多很多，我們通過這些算式發現一個共同的特征，這些算式之所以可以簡便計算，就是有兩個數可以湊整成100（如下式）：

75＋38＋25＝75＋25＋38＝100＋38＝138

38＋75＋25＝38＋（75＋25）＝38＋100＝138

38×75＋38×25＝38×（75＋25）＝38×100＝3800

175-25-75＝175-（25＋75）＝175-100＝75

25×76×4＝25×4×76＝100×76＝7600

76×25×4＝76×（25×4）＝76×100＝7600

25×44＝25×4×11＝100×11＝1100

3700÷25÷4＝3700÷（25×4）＝3700÷100＝37

這樣根據運算律，到最后原本看似復雜的計算都轉變成是與100相加、相減、相乘、相除的口算，計算大大地簡便了。當然，這次我們是湊整成100，還可以湊整成1000、50、10……或者是其他便于口算的數，比如72×25-68×25＝（72-68）×25，雖然72 減68 沒有湊整成100 或整十數，但72 減68 的差4 與25 相乘是一對黃金搭檔，計算也很簡便。