極限工況下漂浮式風電機組塔架的波浪荷載估計

文 | 許楠

已有研究表明，由波浪導致的浮體運動會增加漂浮式風電機組的塔架荷載。若采用專為固定式基礎設計的風電機組，有必要考慮浮體運動對塔架荷載的影響，從而實現風電機組安全性校核。以往對塔架荷載的研究多基于數值模擬結果，風荷載與波浪荷載耦合在一起，不同自由度上的運動影響也耦合在一起。而在實際設計中，浮體設計與塔架設計大多是分開進行的，但考慮到浮體運動會影響塔架荷載，因此，有必要利用浮體運動計算塔架的波浪荷載。

為了提出可靠的波浪荷載解析公式，計算模型的選取十分重要。Takahashi通過在固定式基礎模型的底部施加加速度來考慮浮體運動對塔架荷載的影響，但此模型沒有得到驗證，而且大多數情況下給出的結果并不合理。因此，有必要提出一種等效的模型計算漂浮式風電機組塔架的波浪荷載。本文采用SR（Sway-Rocking）模型分別考慮縱移和縱搖兩種相對顯著的浮體運動，從而可以應用等效靜力荷載方法和模態分析提出塔架波浪荷載的計算解析公式。本文所采用的理論適用于IEC-61400-3中的DLC6.2a，即極限工況下漂浮式風電機組處于停機狀態，不考慮風電機組控制系統對塔架荷載的影響。

SR模型

縱移和縱搖是浮體6個自由度運動（如圖1）中最為顯著的兩個，其他方向的運動可以忽略。因此，本研究借鑒地震工程中常用的SR模型（如圖2）作為等效計算模型模擬浮體運動對塔架荷載的影響。SR模型可將復雜的錨固體系簡化為兩個方向的彈簧和阻尼器：縱移用一個橫向的彈簧和阻尼器模擬，縱搖用一個轉動的彈簧和阻尼器模擬。與地震工程不同的是等效剛度kS、 kR和阻尼cS、 cR需通過FEM分析來獲取。

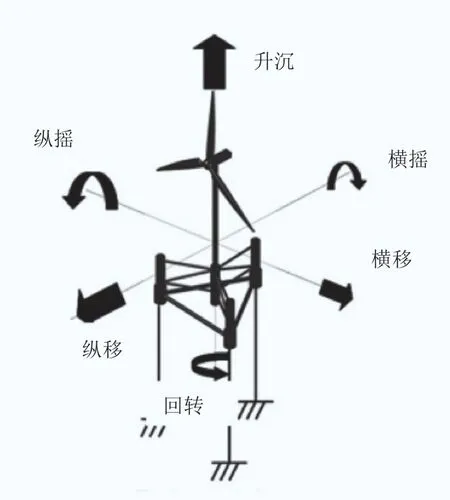
圖1 浮體式風電機組體系的運動

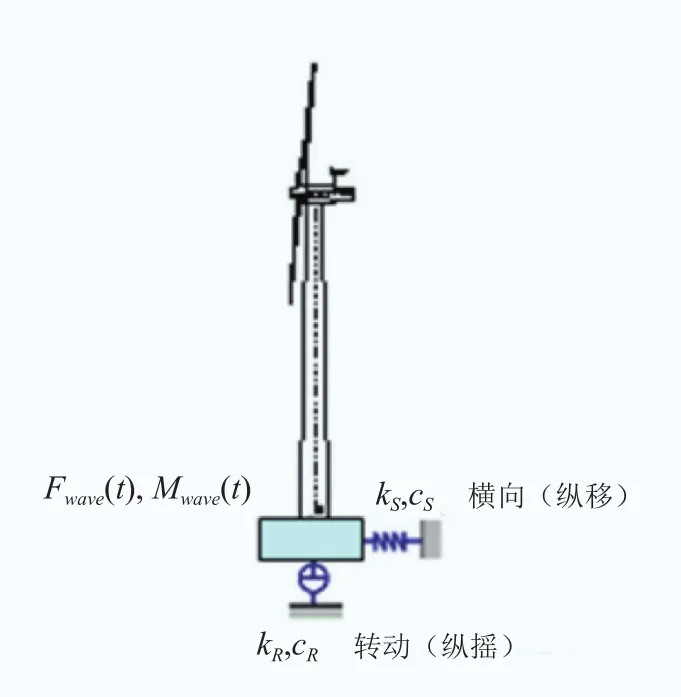
圖2 SR 模型

等效波浪力

應用SR模型，將浮體和風電機組簡化為n個質量節點（如圖3），通過模態分析，可以得出浮體運動，即塔架底部的位移［x1］、 速度［v1］和加速度［a1］，以此可計算作用于浮體上等效波浪力的公式。

如圖3（a）所示，將轉動模態鎖定，只考慮橫向模態，第j 階模態的運動方程為：

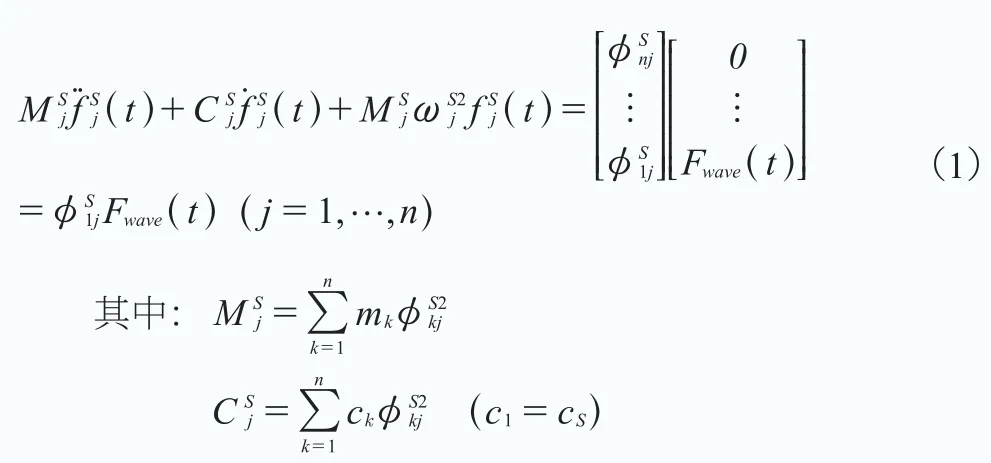
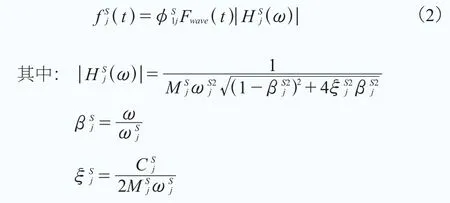
在模態分析中，分別計算不同振動模態下的激勵結果，然后進行疊加。這樣，由公式（2）就可以得出塔架底部的位移：

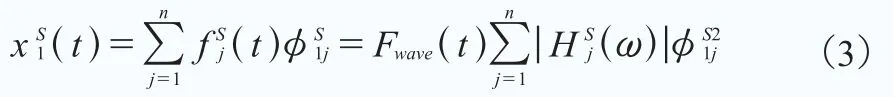
因此，橫向的等效波浪力就可以表達為：

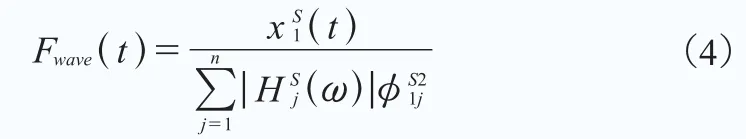
運用同樣的方法，將橫向模態鎖定，只考慮轉動模態，那么如圖3（b）所示的轉動等效波浪力矩也可以由模態分析得出，表達式如下：

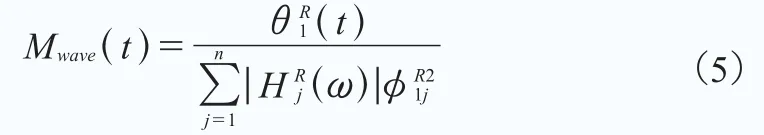
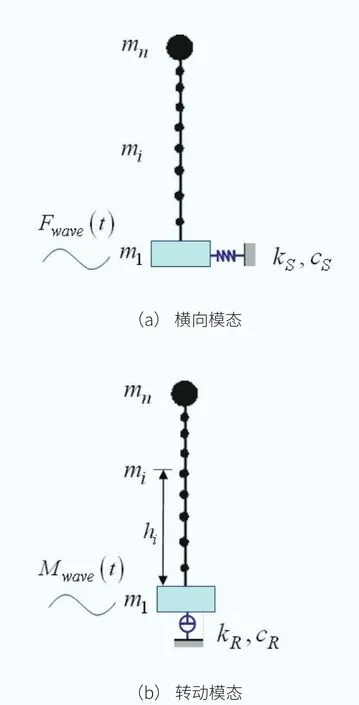
圖3 用于模態分析的計算模型

由公式（4）和（5）可知，等效波浪力和波浪力矩可以由塔架底部的位移、阻尼比、波浪頻率與結構固有頻率的比值以及塔架底部的振型計算得出。獲取了等效波浪力和波浪力矩之后，可以得出塔架波浪荷載的計算解析公式。

波浪荷載估計

基于以上討論，應用SR模型和模態分析能夠得出塔架剪力的解析公式。本文采用FEM計算程序和完整的風電機組、浮體及錨固體系模型來驗證塔架剪力的解析公式，該程序會考慮風電機組、浮體及錨固體系之間的耦合特性。

一、波浪條件

本研究分別考慮了規則波和不規則波。由于線性Airy波是具有單一周期的規則波，因此，采用Airy波結合模態分析來推導塔架剪力，能更容易解釋波浪頻率對結構響應的影響。本研究采用的Airy波的極限波高Hextreme＝20m，波浪周期變化范圍為10～20s，以1s為變化間隔；而在實際環境中，波浪均為不規則波，不規則波以有義波高HS和譜峰周期TP來描述。本研究考慮50年重現期的3小時極限海況。IEC-61400-3中明確指出，在短期的3小時或6小時時間段內，波浪條件可假設為穩定，即有義波高和譜峰周期可假設為不變。因此，本研究采用有義波高為10.75m，譜峰周期變化范圍為10～20s，以1s為變化間隔，并采用工程設計常用的JONSWAP譜生成波浪時程。根據Chakrabarti的研究，生成波浪時程時，波浪的峰值因子取3.3；當ω≤2π/TP時，形狀因子取0.07，當ω＞2π/TP時，形狀因子取0.09。這里，ω是波浪的角頻率。

二、風電機組、浮體與錨固體系

本文研究波浪荷載的模型時選取半潛式浮體作為基礎，錨固體系分別采用張力腿和懸鏈線兩種典型的錨固體系，浮體之上安裝NREL 5-MW型號風電機組。風電機組的詳細參數參見表1；浮體的詳細參數參見表2。對于張力腿錨固體系，考慮到應盡量消減浮體的縱搖效應，3條張力索分別連接浮體的3個角柱，參照圖4（a）；懸鏈線錨固體系由3條400m跨度的錨鏈共同連接在中心柱的底端，相鄰錨鏈水平投影的夾角為120°，其中一條沿入射波的方向伸展，參照圖4（b）。

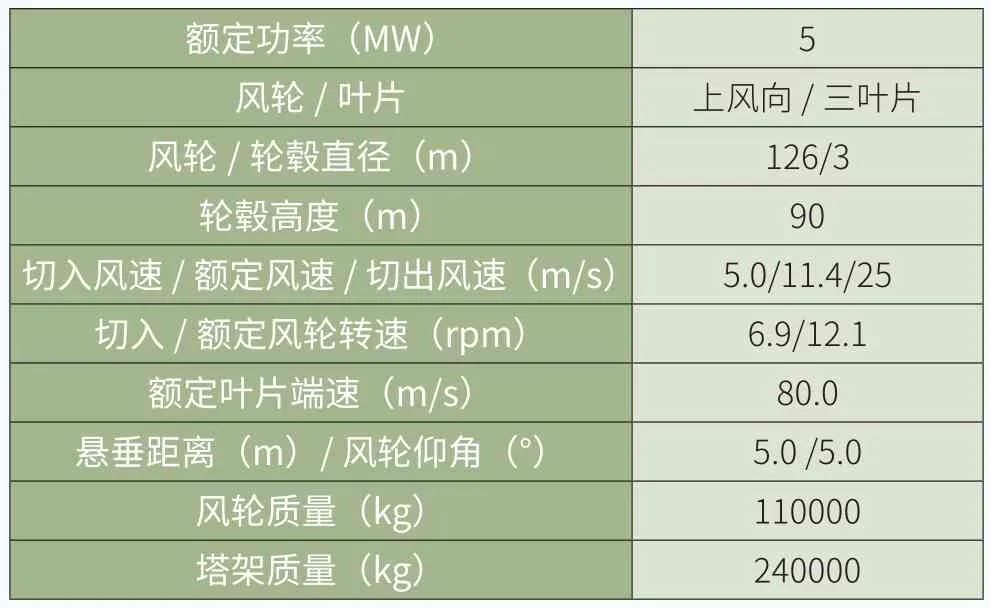
表1 NREL 5-MW風電機組的參數

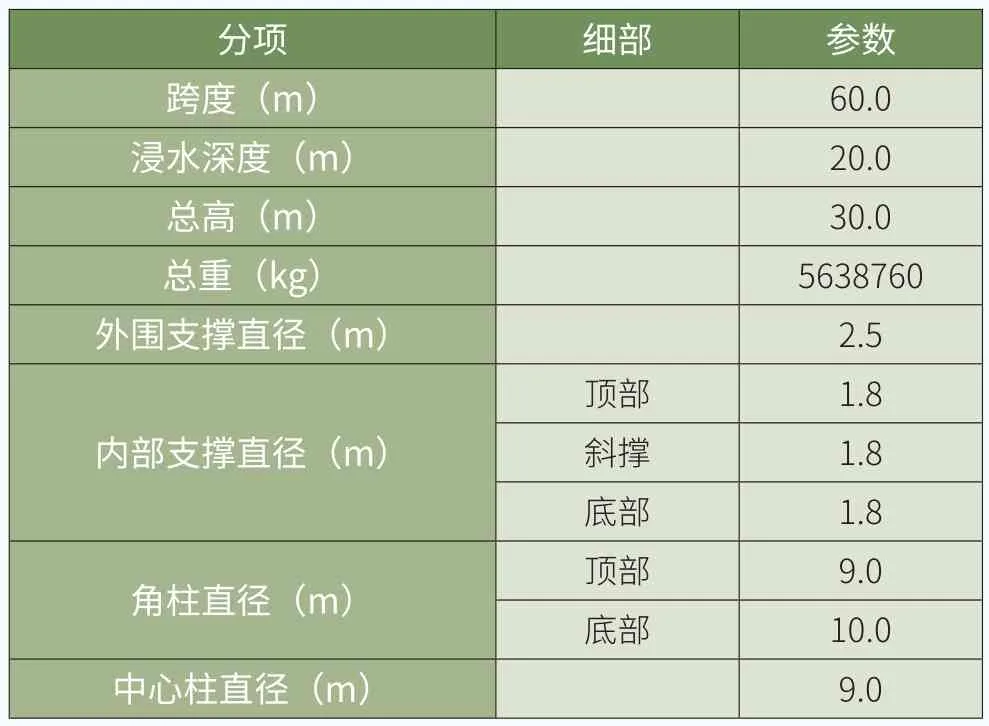
表2 半潛式浮體的參數

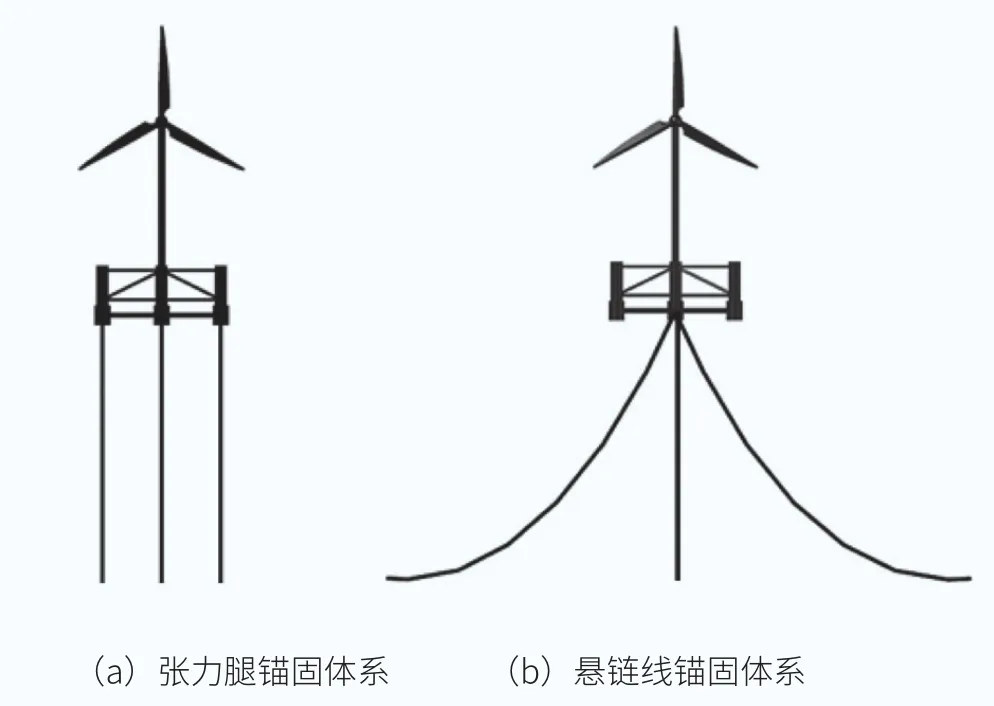
圖4 本文研究的錨固體系

三、塔架剪力

對于圖3中的橫向模態，節點i處的剪力可由塔架底部的響應來計算：

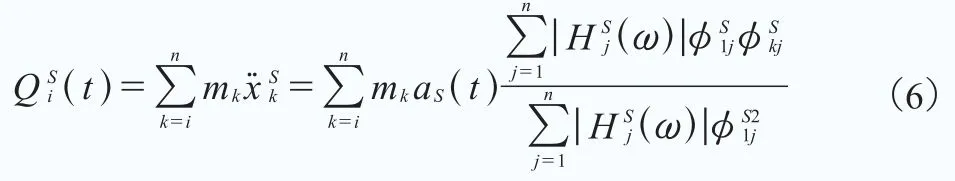
式中，aS（t）是已知的塔架底部橫向加速度。如果僅考慮第一階振型，公式（6）就變為：

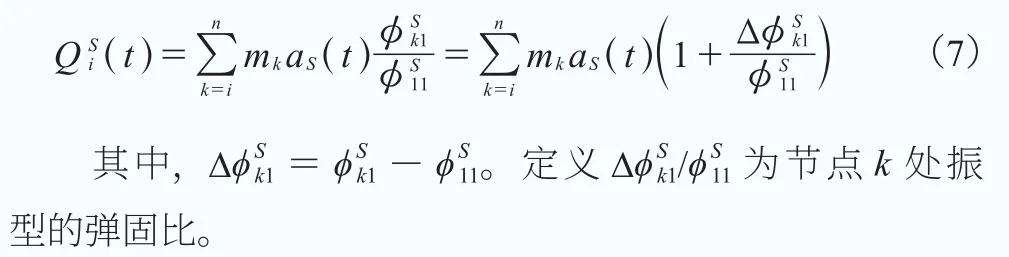
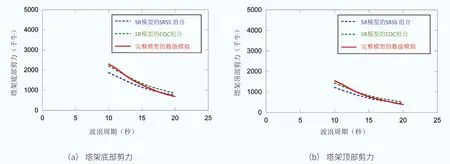
圖5 應用CQC和SRSS方法的剪力組合比較

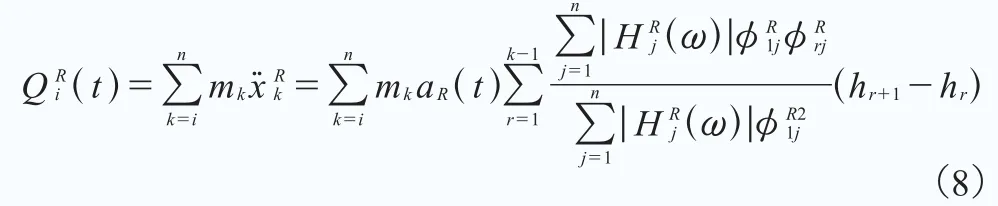
式中，aR（t）是已知的塔架底部轉動加速度。如果僅考慮第一階振型，公式（8）中的剪力就變為：

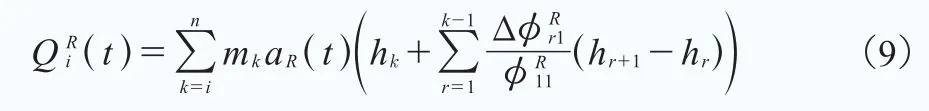
（一）規則波作用下的塔架剪力

對于規則波情況，在公式（7）和（9）中，aS（t）和 aR（t）可以由它們各自的幅值來代替，以計算橫向運動和轉動運動所引起的塔架剪力幅值。

對于張力腿錨固體系，轉動運動對塔架剪力的影響可以忽略不計，因此，塔架剪力可以認為全部由橫向運動產生；而對于懸鏈線錨固體系，橫向運動和轉動運動對塔架剪力均有顯著影響，因此，應將兩種運動產生的影響組合起來。由FEM數值模擬可以發現，橫向運動和轉動運動所產生的最大響應不會同時發生，但它們之間存在一定相關性。參考日本建筑結構荷載規范AIJ （2004）中關于地震荷載的組合方法，本研究采用完全二次方組合法（CQC）。需要注意的是，橫向模態和轉動模態之間的相關性不會隨著外部激勵的變化而發生改變，即波浪力僅依賴于系統的阻尼和固有頻率。

參考AIJ （2004），還有另外一種橫向模態和轉動模態之間的組合方法，即平方和開平方根法（SRSS），這種方法認為兩個模態之間是不相關的。圖5為應用CQC和SRSS方法的剪力組合比較，可以看出SRSS方法低估了塔架剪力；因為橫向模態和轉動模態較為接近特征值，CQC方法可以給出更為準確的結果。

（二）不規則波作用下的塔架剪力

對于不規則波情況，塔架荷載是隨機產生的。因此，本文將采用等效靜力荷載法研究荷載的標準差和峰值因子，用它們的乘積與平均荷載的和來計算最大荷載，而浮體運動產生的塔架荷載的平均值近乎為0，可以忽略不計。

與規則波情況類似，在公式（7）和（9）中，aS（t）和 aR（t）可以由它們各自的標準差來代替，以計算橫向運動和轉動運動所引起的塔架的剪力標準差。對于張力腿錨固體系，塔架剪力標準差可認為全部由橫向運動產生；而對于懸鏈線錨固體系，應將橫向運動和轉動運動所產生的剪力標準差組合起來，組合方法仍采用CQC方法。

如圖6所示為張力腿錨固體系和懸鏈線錨固體系塔架底部剪力的偏度比較。從圖中可以看出，懸鏈線錨固體系的塔架底部剪力的偏度接近0，意味著塔架底部剪力可假設為高斯過程；而張力腿錨固體系塔架底部剪力的偏度在波浪周期不超過15s時較為明顯，應考慮為非高斯過程。為了統一張力腿錨固體系和懸鏈線錨固體系塔架底部剪力峰值因子的計算公式，本研究采用Kareem提出的非高斯峰值因子計算模型，如公式（10）所示。當偏度α3＝0時，公式（10）由非高斯峰值因子變為高斯峰值因子。

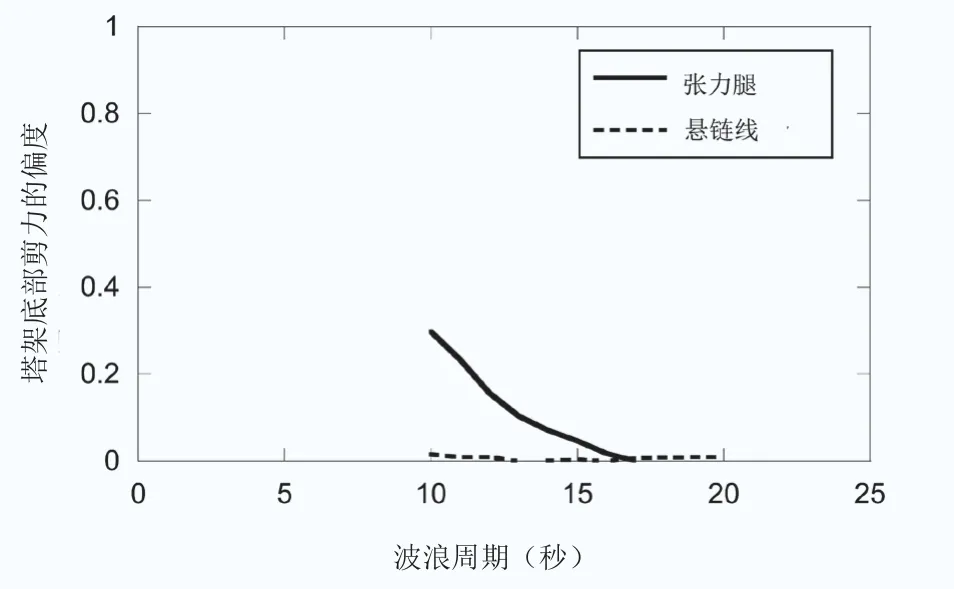
圖6 張力腿錨固體系和懸鏈線錨固體系塔架底部剪力的偏度比較

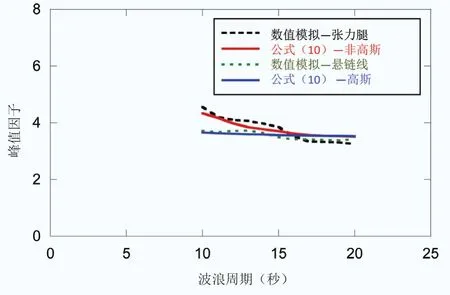
圖7 張力腿錨固體系和懸鏈線錨固體系峰值因子的比較

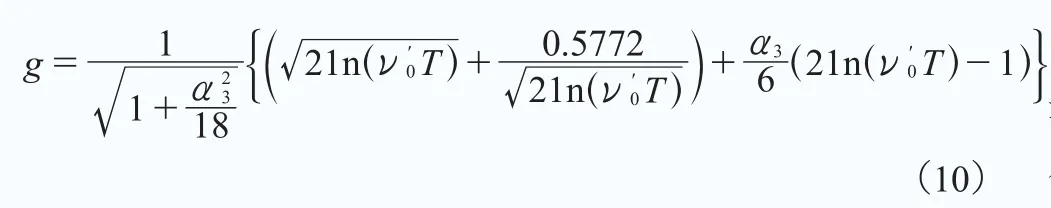
圖7表明，公式（10）可以給出與數值模擬吻合較好的峰值因子結果。對于張力腿錨固體系，有必要采用非高斯峰值因子，而且隨著波浪周期的增加，峰值因子呈減小趨勢，因為其偏度和向上零穿越概率具有同樣的趨勢；而對于懸鏈線錨固體系，高斯峰值因子可以給出較好的結果，并且隨波浪周期變化不大。另外，非高斯峰值因子和高斯峰值因子在波浪周期不超過15s時，差異較大。

結論

本文采用SR模型分別考慮縱移和縱搖兩種相對顯著的浮體運動對塔架荷載的影響，應用等效靜力荷載方法和模態分析提出塔架波浪荷載的計算解析公式。在進行模態分析時，橫向運動或轉動運動所引起的塔架荷載分別采用將另一種模態鎖定的方法來獲得，然后采用CQC方法進行組合，橫向模態和轉動模態之間的相關性僅依賴于系統的阻尼和固有頻率。對于不規則波情況，在計算塔架底部剪力最大值時，張力腿錨固體系有必要采用非高斯峰值因子，而且隨著波浪周期的增加，峰值因子呈減小趨勢；而對于懸鏈線錨固體系，高斯峰值因子可以給出較好的結果，并且隨波浪周期變化不大。

攝影：凃漢溪