考慮土體參數空間變異性的邊坡大變形破壞模式研究*

劉 鑫 王 宇 李典慶

( ①武漢大學水資源與水電工程科學國家重點實驗室 武漢 430072)

( ②香港城市大學建筑學及土木工程學系 香港 999077)

0 引 言

巖土工程中不確定性不可避免，其中一個重要的不確定性是土體參數內在的空間變異性( Phoon et al.，1999; Wang et al.，2016b; 趙晶等，2018) 。由于邊坡總是沿著土體中的最軟弱區域滑動，土體參數的空間變異性與邊坡失穩密切關聯。大量研究已表明土體參數的空間變異性對邊坡失效概率有較大的影響，這些研究大多采用隨機極限平衡方法( Random Limit Equilibrium，RLEM) ( EI Ramly et al.，2002; Cho，2007; 楊 繼 紅 等，2007; Ji et al.，2012; 蔣水華等，2014; 楊智勇等，2019) 或隨機有限元方法( Random Finite Element Method，RFEM)( Griffiths et al.，2004，2009; Hicks et al.，2010; 肖特等，2014; Li et al.，2016a) 。然而，由于極限平衡方法或有限元方法的限制，它們難以模擬土體的大變形破壞過程。實際上，邊坡失穩是一個涉及啟動、滑動和堆積3 個階段的動態過程。但極限平衡方法僅滿足靜態平衡方程( 陳祖煜，2003) ，有限元方法在模擬大變形時可能遇到網格破壞問題導致計算不收斂。邊坡失穩的全過程將決定邊坡的失事后果，因而有必要研究考慮土體參數的空間變異性情形下邊坡的大變形破壞過程及其特征。

近年來，物質點法( Material Point Method，MPM) ( Sulsky et al.，1994; 張雄等，2013) 被廣泛應用于巖土領域的大變形問題中，如邊坡漸進破壞( Zabala et al.，2011; Yerro et al.，2016) 、多相介質失穩( Bandara et al.，2015; Yerro et al.，2015; Wang et al.，2018) 、管涌( Yerro et al.，2017) 、靜力觸探試驗( Ceccato et al.，2016) 等。物質點法與有限元法類似，是一種基于連續介質力學的數值模擬工具。物質點法將問題域同時劃分為歐拉背景網格和拉格朗日物質點，背景網格用于求解動量方程，拉格朗日物質點攜帶材料和場變量( 如速度、加速度) 信息，使物質點可以自由變形，避免了有限元里重新劃分網格帶來的問題( Yerro et al.，2016) 。這使得物質點法適于分析邊坡穩定性分析和大變形破壞全過程( 史卜濤等，2016; 王斌等，2017; 張巍等，2017) 。為了考慮土體參數的空間變異性，已有學者提出了結合直接蒙特卡洛模擬的隨機物質點法( Random Material Point Method，RMPM) ( Wang et al.，2016a) ，但計算消耗較大，阻礙了它在實際工程中的應用。

為此，本文采用一種隨機極限平衡－物質點法分析考慮土體參數的空間變異性情形下的邊坡大變形破壞模式。該方法同時利用極限平衡方法簡單、高效的優勢和物質點方法模擬土體大變形破壞的能力，能夠實現高效的邊坡可靠度分析和風險評估。

1 隨機極限平衡－物質點法

隨機物質點法( Wang et al.，2016a) 一般采用直接蒙特卡洛模擬產生N 個隨機樣本進行不確定分析，邊坡失效概率Pf的表達式為:

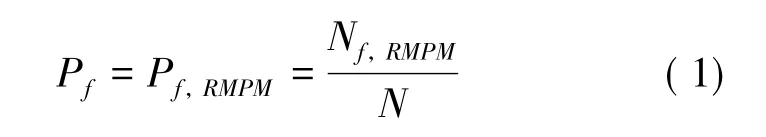
式中，Nf，RMPM為失效樣本總數，即發生土體大變形破壞的隨機樣本數目; N 為隨機樣本總數，建議至少取N=10/Pf保證失效概率估計的變異系數小于0.3( Ang et al.，2007) 。

然而，邊坡失穩通常是小概率事件，直接蒙特卡洛模擬需要產生大量的樣本，考慮到每次物質點法分析本身計算耗時較長，直接蒙特卡洛模擬的計算總耗時可能過高。例如，對于邊坡失效概率Pf=0.001，至少需要產生10 000 個隨機樣本。若采用隨機物質點法完整分析所有樣本，考慮每次分析耗時15 min，不考慮并行情況下計算總耗時將高達15萬分鐘，即2500 h。這對于工程實踐是難以接受的。

事實上，蒙特卡洛模擬的N 個樣本中僅有Nf，RMPM個失效樣本，其他的未失效樣本占大部分，對應在物質點法分析中沒有發生大變形破壞。所以沒有必要采用物質點法分析這些穩定的樣本，這樣可以大大提高計算效率。

本文提出的隨機極限平衡－物質點法將結合隨機極限平衡方法的計算效率優勢和隨機物質點方法模擬大變形破壞的能力，用于高效的邊坡可靠度分析與風險評估( Liu et al.，2019) 。圖1 繪制了本文方法的框架，包含4 個部分。第1 部分是采用傳統極限平衡方法和物質點方法分別建立確定性分析的邊坡模型，并保證兩個模型的一致性，即擁有相同的幾何形狀、土體參數等。第2 部分采用隨機場理論( Vanmarcke，2010) 作為不確定性模型模擬空間變異的土體，許多文獻( 蔣水華等，2014; 肖特等，2014) 已有介紹，這里不再贅述。第3 部分是采用蒙特卡洛模擬進行不確定性分析。第4 部分為結果后處理，處理隨機極限平衡方法和隨機物質點方法得到的結果，如計算邊坡失效概率，研究邊坡大變形破壞模式等。

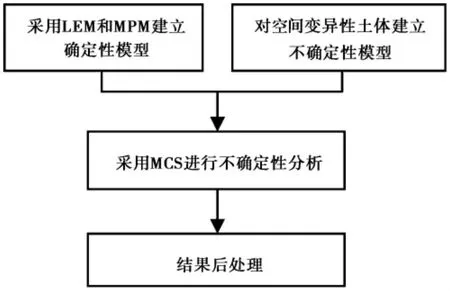
圖1 隨機極限平衡－物質點法框架Fig. 1 Illustration of the proposed framework

首先利用蒙特卡洛模擬產生N 個隨機場樣本，采用隨機極限平衡方法進行不確定性分析，計算所有隨機場樣本的安全系數值。由于隨機極限平衡方法計算簡便、耗時短，可以輕易地完成N 個隨機場樣本的不確定性分析。接下來將所有隨機場樣本根據安全系數值從小到大排序，后續計算過程被劃分為k 個迭代步。對于第k=1 次迭代，從排序后的樣本序列中取第1 個隨機場樣本采用隨機物質點分析，判斷是否發生大變形破壞，若發生破壞則令失效樣本總數目加1，采用式( 1) 計算失效概率。若不滿足終止條件，則迭代步k=k+1。對于第k 次迭代( k＞1) ，從排序后的樣本序列中取第k 個隨機場樣本采用隨機物質點方法分析，判斷是否發生大變形破壞，若發生破壞則更新失效樣本數目，并采用式(1) 計算失效概率。迭代計算的終止條件定義為當失效概率收斂到一個確定的值，即迭代過程中計算的失效概率經過kt個迭代步保持幾乎不變。根據經驗，kt可取為1%～10%的樣本總數目N。

2 邊坡大變形破壞模式

為了驗證本文提出的隨機極限平衡－物質點法，采用一個雙層土坡算例分析。圖2 繪制了該土坡的幾何形狀。上層土高18 m，下層土高10 m，坡比為3︰4，水平距離被延長到112 m 用于堆積滑動體。已有研究采用隨機有限元方法對該土坡進行可靠度分析( Li et al.，2016b) ，為了保持一致，土體參數取自該文獻。兩層土的重度均等于19 kN·m－3。兩層土的不排水強度均服從對數正態分布。上層土不排水強度的均值為80 kPa，變異系數為0.30; 下層土不排水強度的均值為120 kPa，變異系數為0.30。采用指數型隨機場模擬土體不排水強度的空間變異性，有關細節可參考文獻( Li et al.，2015) 。水平相關長度為24 m，豎直相關長度為2.4 m。圖2 繪制了隨機場網格，網格大小為1 m×1 m，采用喬列斯基分解離散隨機場。

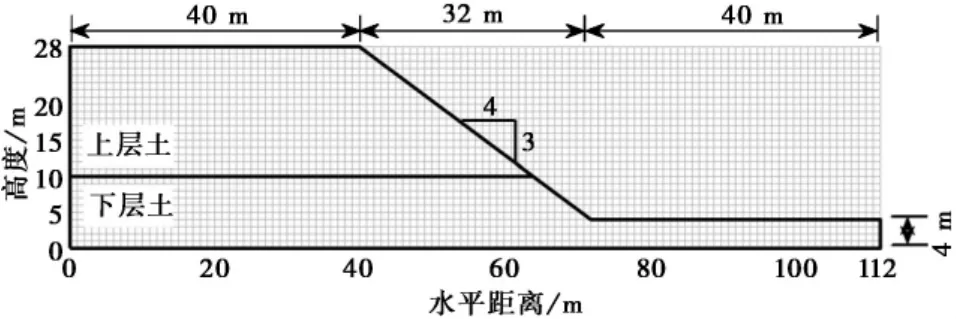
圖2 二層土坡幾何形狀Fig. 2 Geometry of a two-layer soil slope

對于邊坡穩定分析，本文與前人一樣假設滑動面為圓弧形并采用簡化畢肖普法計算邊坡安全系數。對于物質點方法分析，整個區域被離散為1 m×1 m 的網格，每個網格均勻分布4 個物質點。采用考慮線性軟化的Drucker-Prager 模型作為本構模擬土體 的 彈 塑 性( Bandara et al.，2015; Wang et al.，2018) 。土體的殘余強度取原始強度的50%，硬化模量為－50 kPa( 即軟化) 。物質點法總模擬時長為20 s，每個時間步長約為0.000 75 s，重力加速度等于9.81 m·s－2。

首先采用直接蒙特卡洛模擬產生40 000 個隨機場樣本，采用文中的隨機極限平衡－物質點方法分析每個隨機場樣本是否發生大變形破壞( 閾值為最大相對位移超過1 m，見Liu et al. ( 2019) ) 。最終得到一共有520 個樣本發生破壞，對應隨機物質點方法的失效概率等于Pf，RLEM=520/40000=1.30×10－2。該失效概率與隨機極限平衡方法得到的1.12×10－2和隨機有限元方法( Li et al.，2016b) 得到的1.06×10－2較為吻合。使用本文方法，無需采用隨機物質點方法分析全部40 000 個隨機場樣本，實際僅耗費2512 個隨機場樣本即達到收斂，計算消耗僅約為原直接蒙特卡洛模擬的6%，大大提高了計算效率。

對于本算例，本文方法通過隨機物質點方法分析可得到不同的破壞模式，根據滑動深度不同，可劃分為淺層、深層、中層破壞模式，另外還有漸進破壞模式涉及到多重破壞模式同時或漸進發生。

2.1 淺層破壞模式

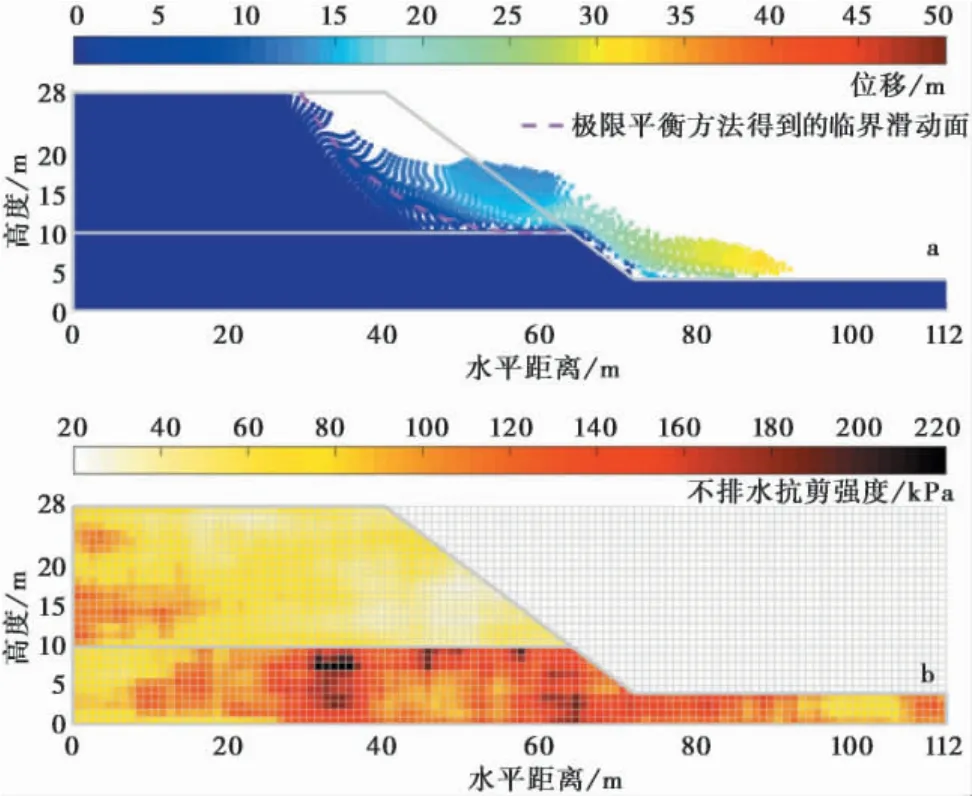
圖3 邊坡淺層破壞模式位移與不排水抗剪強度分布Fig. 3 Displacement and undrained shear strength distributions of a shallow slope failure mode

圖3a、圖3b 分別繪制了一種典型邊坡淺層破壞模式的位移與不排水抗剪強度分布圖。對于本算例，淺層破壞模式被定義為僅發生在上層土體。該破壞模式土體沿著上下層土的交界面滑動，順著坡面下滑并堆積在坡腳處。圖3 顯示該破壞模式發生位移約為30 m。極限平衡方法得到的臨界滑動面( 即對應安全系數最小的滑動面) 與物質點法中實際發生的滑動體形態較為一致。如圖3b 所示，上層土靠近坡面部分的不排水抗剪強度較低，低于左側土體，顯著低于下層土。這種情況容易產生淺層破壞。

2.2 深層破壞模式

圖4a 繪制了一種典型的深層破壞模式。深層破壞模式被定義為滑動帶底部低于坡腳高度的破壞模式。該破壞模式滑動體積一般大于淺層破壞模式。該滑動體整體沿著某一個圓心轉動發生失穩，滑動體形態保持較為完整，故被細分為徑向深層破壞模式。圖4b 繪制了對應的不排水強度分布。下層土底部及坡腳附近的不排水抗剪強度均較低，且下層土的軟弱區與上層土的軟弱區相連形成了弧形軟弱帶，可能促使徑向深層滑動模式的發生。

圖5a 繪制了另一種典型的深層破壞模式。與圖4a 繪制的徑向深層破壞模式不同，圖5a 中滑動體主要沿著邊坡底部水平切向滑動，轉動較小。且滑動體被分為兩個三角形的滑動體，兩個滑動體之間存在明顯的錯動帶。這可能是由于滑動體前后的滑動速度不一致造成滑動體沿著某個傾斜的軟弱帶發生錯動。這種破壞模式被分類為切向深層破壞模式。該破壞模式的滑動距離約為24 m，大于圖4a中的徑向深層滑動模式。從圖5b 中可以看出下層土的底部存在連續的水平軟弱帶，使得滑動體更易于沿著底部水平運動。值得注意的是，該破壞模式的形態不符合圓弧滑動面假設，說明圓弧滑動面的假設在考慮土體參數的空間變異性情形時可能不成立。

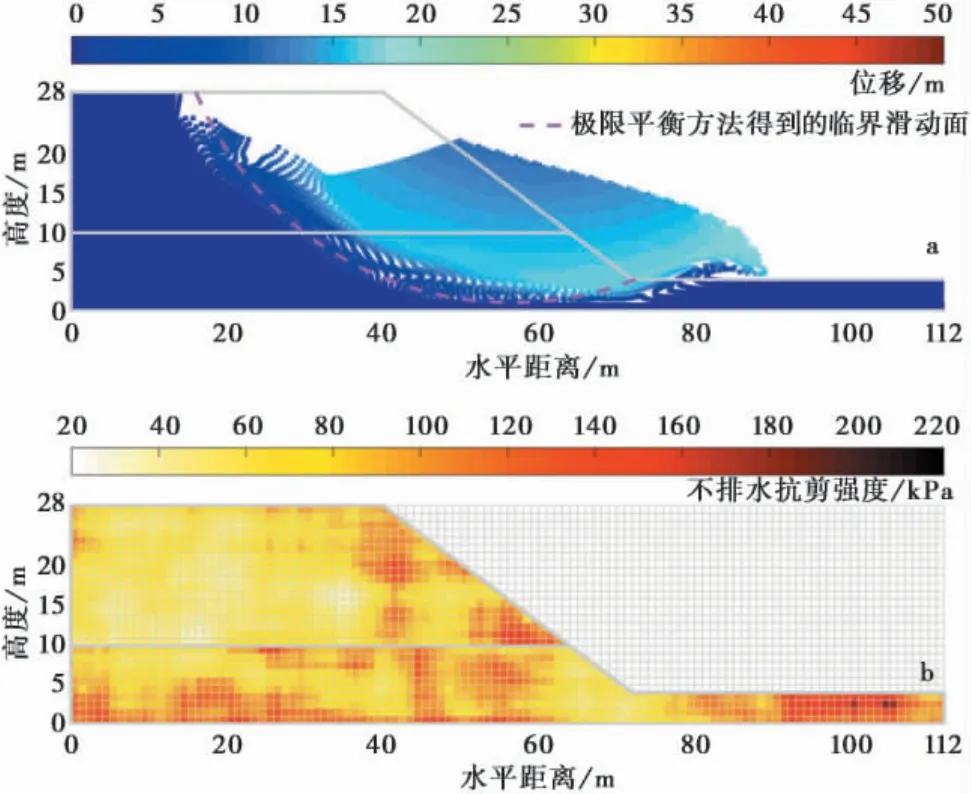
圖4 邊坡徑向深層破壞模式位移與不排水抗剪強度分布Fig. 4 Displacement and undrained shear strength distributions of a radial deep slope failure mode

圖5 邊坡切向深層破壞模式位移與不排水抗剪強度分布Fig. 5 Displacement and undrained shear strength distributions of a tangential deep slope failure mode

2.3 中層破壞模式

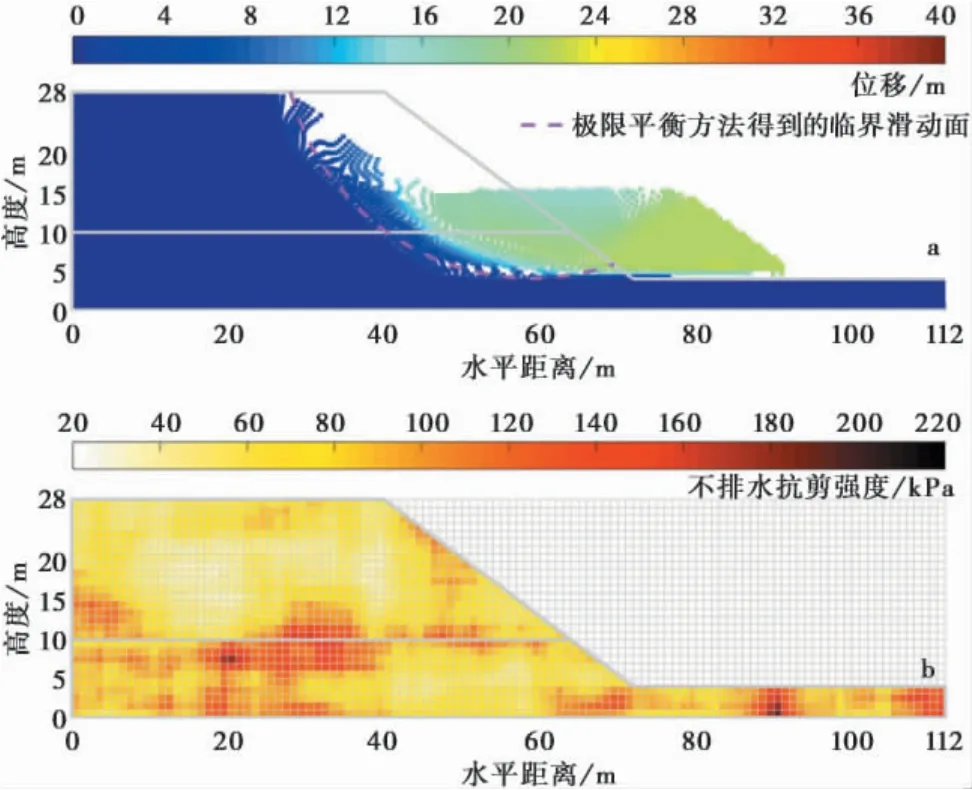
圖6 邊坡中層破壞模式位移與不排水抗剪強度分布Fig. 6 Displacement and undrained shear strength distributions of an intermediate slope failure mode

中層破壞模式的滑動深度介于淺層和深層破壞模式之間，通常沿著坡腳切向滑動。圖6a 繪制了一種典型的中層破壞模式的位移分布。與淺層破壞模式相比，中層破壞模式的滑動體積更大; 與深層破壞模式相比，滑動體的重力勢能轉換為動能后無需抵抗重力做功，故中層破壞模式的滑動距離通常大于淺層和深層破壞模式。圖6b 繪制了該破壞模式的不排水抗剪強度分布。可以看出，坡腳高度之上的軟弱區與上層土的軟弱區相連，坡腳以下土體強度相對較高，從而導致了這種破壞模式。

2.4 漸進破壞模式

除此之外，本研究還發現了漸進破壞模式，即多種破壞模式同時或漸進發生。圖7 繪制了一種典型的漸進破壞模式。圖7a 和圖7b 顯示了時間為第4 s 和第8 s 時一個中層破壞模式在滑動，滑動形態與極限平衡方法得到的臨界滑動面一致。圖7c表明在第10 s 時一個新的淺層破壞模式逐漸形成，最終破壞形態見圖7d，最終滑動距離達到40 m。由于漸進破壞模式涉及到多種破壞模式的發生，多個模式的滑動體積更大，滑動距離更遠，造成的后果通常更為嚴重。需要指出的是，由于極限平衡方法或有限元方法難以模擬土體的大變形破壞全過程，它們難以得到后續的破壞模式，也就無法用于分析漸進破壞模式。說明了物質點法在模擬邊坡大變形破壞全過程的優勢。

圖8 繪制了漸進破壞模式對應的不排水抗剪強度分布。它的土體不排水抗剪強度分布與中層破壞模式的類似，但上層土的強度較低，上層土在第1個中層破壞模式發生后失去支撐，導致了第2 個淺層破壞模式的發生。

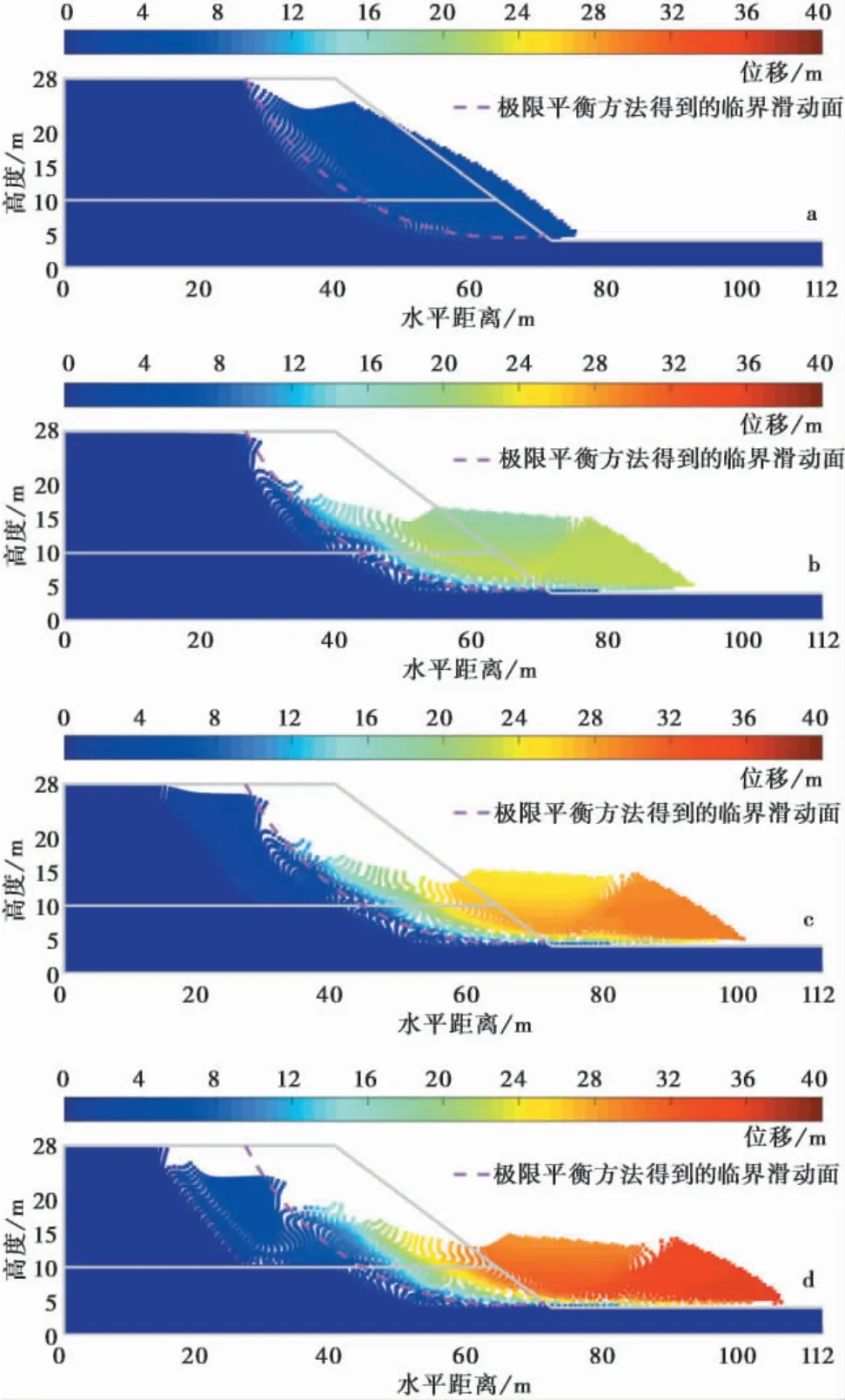
圖7 邊坡漸進破壞模式位移演化Fig. 7 The displacement evolution of a progressive slope failure mode

3 結 論

本文采用隨機極限平衡－物質點法分析了考慮土體參數空間變異性的邊坡大變形破壞模式，得到了包括淺層、中層、深層和漸進一共4 種典型破壞模式，并分析了對應不排水抗剪強度與邊坡破壞模式之間的關系。得到如下結論:

(1) 邊坡的破壞模式與土體強度參數的空間分布密切相關。不同的土體強度參數空間分布可能引起不同的破壞模式，導致不同的失事后果。因此，在進行邊坡風險評估與加固時，應重視勘察工作與勘察數據的利用，盡可能地量化土體參數的空間變異性。從而針對不同的可能破壞模式，做出更有效的加固措施。

( 2) 與極限平衡方法和有限元方法相比，物質點法具備土體大變形分析的能力，既可用于分析邊坡是否失穩，又具備模擬邊坡土體大變形破壞的全過程的能力。本研究提出的隨機極限平衡－物質點法可以同時利用極限平衡方法的計算效率優勢和物質點方法的土體大變形分析能力，可以實現高效地邊坡風險評估。

( 3) 在考慮土體參數的空間變異性時，多數情況下極限平衡方法得到的圓弧滑動面與物質點法得到的滑動體形態較為一致，但在某些情況下圓弧滑動面假設可能失效( 如存在較大連通區域的軟弱帶時) 。此外，極限平衡方法難以用于考慮漸進破壞模式，即多個破壞模式同時或漸進發生情形。

( 4) 本文所采用的物質點方法僅分析單相土體，未來仍需拓展到多相用于考慮土－水的耦合作用，考慮孔隙水壓力等更復雜工況。本文提出的隨機極限平衡－物質點法仍然可用于邊坡可靠度分析和風險評估。

( 5) 可以看出與傳統有限元方法相比，物質點法適于邊坡和其他巖土問題的大變形模擬和破壞分析，可以利用現有的土體本構模型，但物質點法在巖土領域的研究尚處于初期階段，存在一些問題有待完善，如考慮土－水的多相耦合作用、隱式物質點法、應力波動和與有限元相比計算精度不高等問題。