多諧差相信號激勵(lì)下的頻率特性測試方法研究

宿常鵬，王雪梅，許哲，李駿霄，王迪

(1.火箭軍工程大學(xué)，陜西 西安 710025；2.火箭軍士官學(xué)校，山東 青州 262500)

0 引言

伺服機(jī)構(gòu)作為導(dǎo)彈控制系統(tǒng)的執(zhí)行機(jī)構(gòu)，其動(dòng)態(tài)性能直接影響了導(dǎo)彈飛行控制的精度。頻率特性作為衡量動(dòng)態(tài)性能的重要指標(biāo)，是伺服機(jī)構(gòu)測試的重要內(nèi)容。目前，伺服機(jī)構(gòu)的頻率特性測試仍采用傳統(tǒng)的正弦相關(guān)分析法，該方法雖然測試精度高，但是測試速度慢、測試效率低的問題十分突出。

近年來，在頻率特性的快速測試方面已經(jīng)取得了許多進(jìn)展，如文獻(xiàn)[1]提出了一種基于調(diào)頻脈沖掃頻信號的頻率特性測試方法，可在起始頻率和終止頻率按線性或指數(shù)方式充分激勵(lì)系統(tǒng)，提高了測試速度和測試效率，但對干擾信號敏感。文獻(xiàn)[2]提出了基于偽隨機(jī)信號相關(guān)辨識的測試方法，能夠?qū)崿F(xiàn)頻率特性的在線測試，但可重復(fù)性差，測試精度不高。文獻(xiàn)[3]提出了以多頻聲信號為激勵(lì)信號，采用相關(guān)分析法進(jìn)行數(shù)據(jù)處理的頻率特性測試方法，該方法明顯縮短了測試時(shí)間，但是信號波動(dòng)程度大影響測試精度。文獻(xiàn)[4]研究了以多諧差相信號為激勵(lì)信號，采用最小二乘法進(jìn)行數(shù)據(jù)處理的頻率特性測試方法，顯著提高了測試精度和速度，但求解過程中容易遇到數(shù)字病態(tài)問題。

本文從激勵(lì)信號和數(shù)據(jù)處理算法2個(gè)方面對多諧差相信號測試法進(jìn)行了改進(jìn)。首先，提出了功率調(diào)制和相位修正2種方法降低多諧差相信號的峰值因子。其次，通過采用鏡像映射法進(jìn)行數(shù)據(jù)處理，有效避免了方程求解的數(shù)字病態(tài)問題。最后，以某型導(dǎo)彈的伺服機(jī)構(gòu)為測試對象，分別在無噪聲和有噪聲的條件下進(jìn)行仿真，對比正弦相關(guān)分析法的測試結(jié)果，驗(yàn)證了改進(jìn)方法的有效性。

1 多諧差相信號研究

Schroeder M.R[5]于1970年提出了多諧差相信號(Schroeder phased harmonic signal，SPHS)的概念。它是一種由若干個(gè)功率、周期和初相有一定關(guān)系的余弦波疊加而成的多頻信號。其表達(dá)式為

(1)

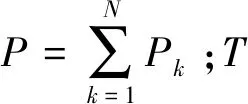
多諧差相信號采用Schroeder相位編碼準(zhǔn)則調(diào)整各余弦分量初相，以降低信號的峰值因子，表達(dá)式為

(2)

(3)

在許多應(yīng)用中，相角必須限制為0和π，這對應(yīng)于在時(shí)間上對稱的波形。將相位編碼公式舍入到π的整數(shù)倍后，式(2)簡化為

(4)

式中：[*]表示向0取整運(yùn)算。

對于均勻功率譜信號，式(3)可簡化為

(5)

作為衡量信號波動(dòng)幅度大小和激勵(lì)是否均勻平穩(wěn)的標(biāo)準(zhǔn)[6]，峰值因子的定義為

(6)

以參數(shù)為N=16，T=0.5 s，P=1 W的多諧差相信號為例，均勻功率譜的多諧差相信號峰值因子為1.89，其波形如圖1所示。若對諧波功率采用正弦調(diào)制方式產(chǎn)生非均勻功率譜信號，信號的峰值因子降為1.64。正弦調(diào)制的通式為

(7)

若在均勻功率譜信號的相位編碼公式中添加修正項(xiàng)ε，根據(jù)取整運(yùn)算的性質(zhì)可得ε∈(0,1)。修正項(xiàng)的選取屬于只含上下限約束的單目標(biāo)優(yōu)化問題，可以通過遺傳算法確定使信號的峰值因子最優(yōu)時(shí)ε的取值。故ε取0.5時(shí)，信號的峰值因子降為1.74。加修正的相位編碼公式為

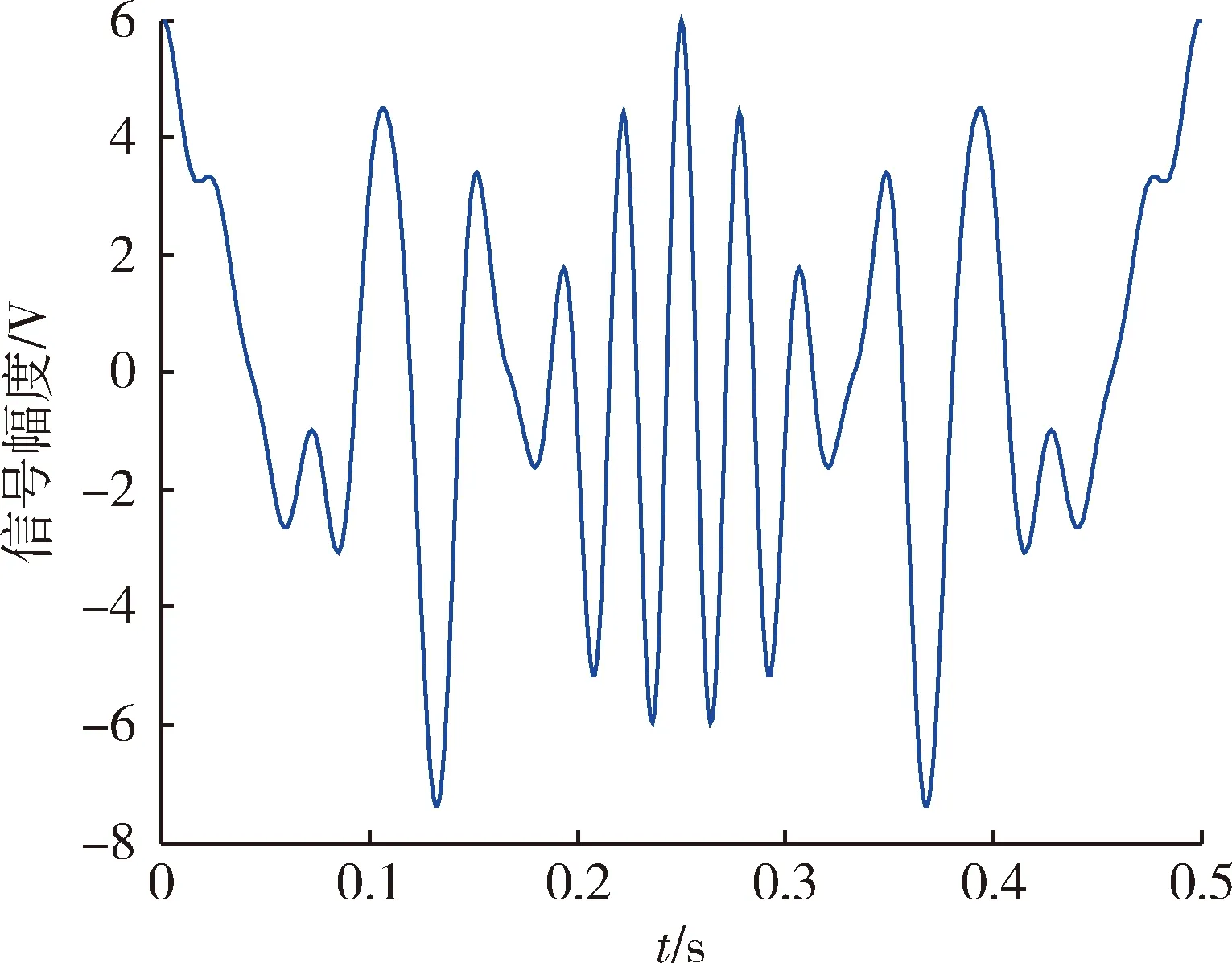
圖1 多諧差相信號波形Fig.1 Waveform of SPHS

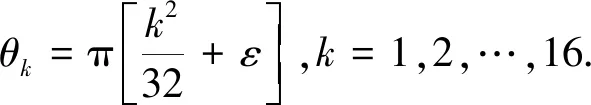
(8)

由圖1可得，多諧差相信號以基波周期T為周期，作快速傅里葉變換時(shí)可通過整周截?cái)啾苊庾V泄漏[8]。而且信號的頻譜是離散的，只在基頻的整數(shù)倍上有能量，可以抑制大部分的噪聲干擾[9]。通過改變基波周期T和諧波數(shù)N可以調(diào)整測試頻帶，實(shí)現(xiàn)對任意頻率點(diǎn)模態(tài)的激活[10]。此外，該信號可以一次性激勵(lì)多個(gè)頻率點(diǎn)的模態(tài)，提高了測試速度。

2 多諧差相信號測試法改進(jìn)

(9)

式中：ak，θk分別為激勵(lì)信號第k次諧波的幅值和初相；bk，φk分別為系統(tǒng)響應(yīng)第k次諧波的幅值和相移。將式(9)按照余弦函數(shù)和角公式展開得

(10)

Yn×1=An×2NC2N×1，

(11)

式中：

YT=[y(0),y(ts),y(2ts),…,y((n-1)ts)]1×n；

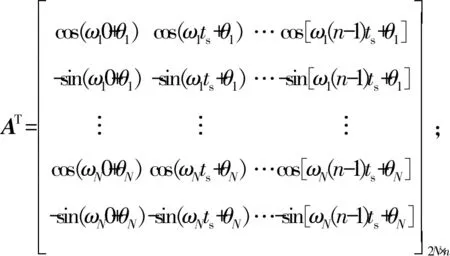
矩陣A由多諧差相信號各次諧波的角頻率和初相構(gòu)造，Y通過對系統(tǒng)的輸出y(t)采樣得到。當(dāng)采樣點(diǎn)數(shù)n足夠大,方程個(gè)數(shù)超過未知數(shù)個(gè)數(shù)，式(11)變?yōu)槌ǚ匠探M。通過求解超定方程組的C陣，即可得到系統(tǒng)響應(yīng)中各次諧波的幅值bk和相移φk，進(jìn)而得到系統(tǒng)的頻率特性。

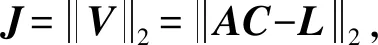
設(shè)存在正交矩陣Hn×n，使得

(12)

記Hn×nL中前2N個(gè)元素為m，其余元素記為g，對殘差方程進(jìn)行正交變換

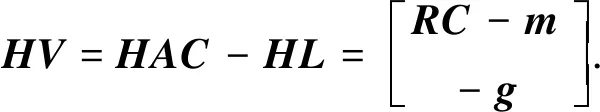
(13)

在正交變換下，向量的長度不變，對式(13)取二次范數(shù)得

(14)

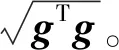
由此可得，角頻率ωk對應(yīng)的幅值比L(ωk)和相位差φ(ωk)為

針對獎(jiǎng)學(xué)金、優(yōu)團(tuán)優(yōu)干以及優(yōu)秀畢業(yè)生等評優(yōu)工作，也可以利用大數(shù)據(jù)對學(xué)生進(jìn)行多個(gè)維度的考核。綜合學(xué)生自身的上課出勤、發(fā)言以及作業(yè)質(zhì)量、社團(tuán)活動(dòng)、課外競賽等多個(gè)方面，利用具體提供的數(shù)據(jù)對學(xué)生展開評比，更加全面地掌握學(xué)生的學(xué)習(xí)態(tài)度、實(shí)踐能力、探索精神、人際關(guān)系以及意志等多個(gè)方面。多維度的評估工作不僅僅局限于對學(xué)生的智力進(jìn)行考核，還需要對學(xué)生的內(nèi)在元素進(jìn)行挖掘，這樣也能為學(xué)生提供相應(yīng)的引導(dǎo)，進(jìn)而優(yōu)化學(xué)習(xí)的模式，使學(xué)生能夠更好地適應(yīng)社會的發(fā)展需要，促進(jìn)高校人才培養(yǎng)質(zhì)量的提升。

(15)

(16)

上述過程可用圖2表示。

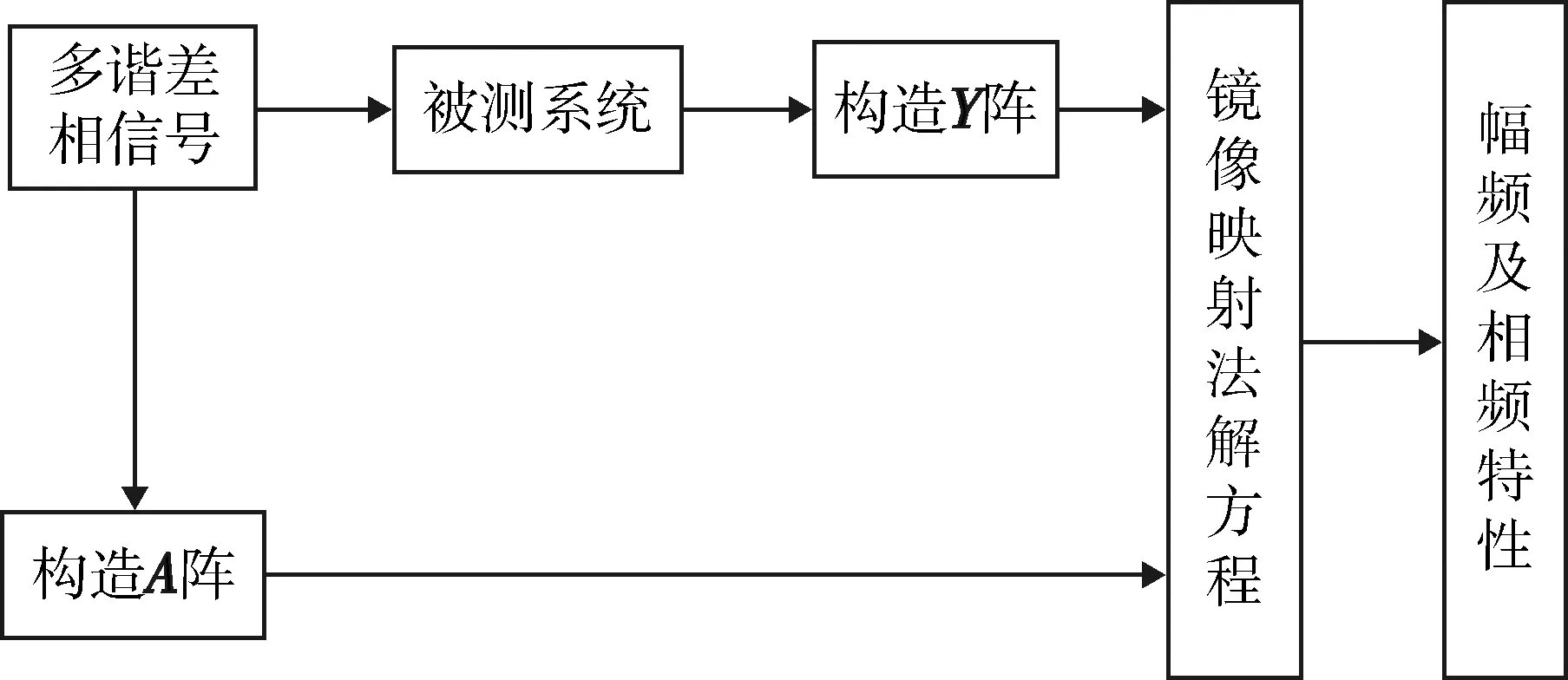
圖2 多諧差相信號測試法原理Fig.2 Schematic diagram of SPHS test method

3 仿真實(shí)驗(yàn)與分析

為驗(yàn)證改進(jìn)的多諧差相信號測試法的測試效果，以某型導(dǎo)彈的電液伺服機(jī)構(gòu)為測試對象，分別使用傳統(tǒng)的正弦相關(guān)分析法和改進(jìn)的多諧差相信號測試法進(jìn)行仿真。忽略系統(tǒng)中電液伺服閥的動(dòng)態(tài)特性、結(jié)構(gòu)變形和非線性摩擦等因素的影響[12]，本文研究的伺服機(jī)構(gòu)由于高階項(xiàng)系數(shù)較小，且頻率測試范圍較小，可近似為二階的線性定常系統(tǒng)，其傳遞函數(shù)為

(17)

3.1 測試效果分析

考慮到伺服機(jī)構(gòu)的最大工作頻率為20 Hz，故將正弦相關(guān)分析法的測試頻率選取0.1,0.5,1,5,10,15,20 Hz，多諧差相信號測試法測試頻率范圍0.1～20 Hz。測試信號的幅值一般取系統(tǒng)額定工作信號的5%～25%，且幅值盡可能大些，在同等噪聲條件下可以提高信噪比[13]。故正弦相關(guān)分析法各頻率點(diǎn)處的正弦激勵(lì)信號的幅值取1 V，多諧差相信號的參數(shù)設(shè)置為：N=200，T=10 s，P=1 W，此時(shí)信號的幅值約為2 V，滿足上述要求。對于參數(shù)為N=200，T=10 s，P=1 W的多諧差相信號，均勻功率譜信號、加修正的均勻功率譜信號和非均勻功率譜信號的峰值因子分別為2.26,2.03,2.17，故選擇加修正的均勻功率譜信號作為激勵(lì)信號，此時(shí)修正項(xiàng)ε=0.3，信號波形如圖3所示。

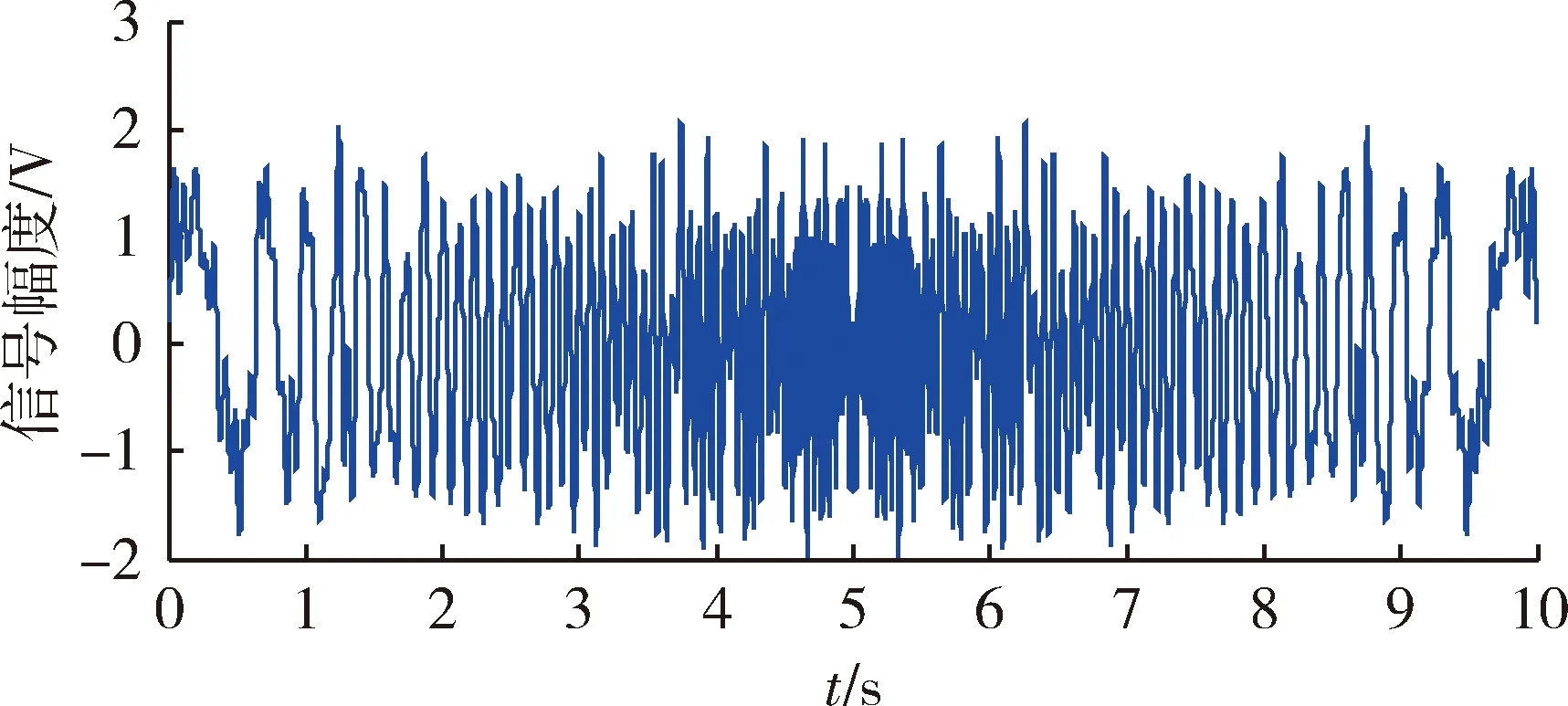
圖3 激勵(lì)信號波形Fig.3 Waveform of excitation signal

工程中，信號的采樣頻率一般選取最高頻率分量的20～50倍。當(dāng)選擇的采樣頻率較低時(shí)，難以保證測試精度。當(dāng)采樣頻率過高時(shí)，又增加了計(jì)算量，降低測試速度。由于仿真過程中信號的最高頻率為20 Hz，故采樣頻率選擇1 kHz。以伺服機(jī)構(gòu)的傳遞函數(shù)得到的理論頻率特性為基準(zhǔn)，研究方法的測試效果。

對于正弦相關(guān)分析法，仿真過程中各頻率點(diǎn)的掃頻時(shí)間取測試頻率點(diǎn)的最大周期。由于測試中正弦激勵(lì)信號的最小頻率為0.1 Hz，故每個(gè)頻率點(diǎn)正弦信號的掃頻周期為10 s。應(yīng)用正弦相關(guān)分析法測得的頻率特性曲線及其誤差曲線如圖4所示。

對于多諧差相信號測試法，頻率特性的測試精度受激勵(lì)時(shí)間的影響。激勵(lì)時(shí)間越長，其頻率特性的測試誤差越小。當(dāng)施加4個(gè)周期的多諧差相信號時(shí)，此時(shí)再增加激勵(lì)時(shí)間對提高測試精度的作用不再明顯，故選擇施加4個(gè)周期的激勵(lì)信號進(jìn)行仿真。應(yīng)用多諧差相信號測試法測得的頻率特性曲線及其誤差曲線如圖5所示。

由圖4和圖5可得，在測試精度方面，正弦相關(guān)分析法的幅頻特性測試誤差約為0.03 dB，相頻特性測試誤差約為1.5°，多諧差相信號測試法的幅頻特性測試誤差約為0.79 dB，相頻特性測試誤差約為0.6°。可見，正弦相關(guān)分析法的幅頻特性測試精度更高，多諧差相信號測試法的相頻特性測試精度更高。在測試時(shí)間方面，正弦相關(guān)分析法需要對7個(gè)頻率點(diǎn)處的頻率特性進(jìn)行測試，每個(gè)頻率點(diǎn)正弦信號的掃頻周期為10 s，故施加激勵(lì)信號時(shí)間共計(jì)70 s。而多諧差相信號測試法則一次性測試200個(gè)頻率點(diǎn)處的頻率特性，施加4個(gè)周期的多諧差相信號共計(jì)40 s，時(shí)間縮短了43%，有效提高了測試速度和測試效率。

圖4 正弦相關(guān)分析法測得頻率特性及誤差曲線Fig.4 Frequency characteristic and error curve obtained by sinusoidal correlation analysis method

3.2 抗干擾能力分析

實(shí)際測試會受到噪聲干擾，為研究多諧差相信號測試法受噪聲干擾的影響，在模型輸出端加入均值為0、方差為0.01的高斯白噪聲進(jìn)行仿真[14]。

加噪聲后正弦相關(guān)分析法測得的頻率特性及其誤差曲線如圖6所示。由圖6可得，正弦相關(guān)分析法由于相關(guān)運(yùn)算對噪聲的抑制作用較強(qiáng)，測試誤差較小，其幅頻特性測試誤差約0.1 dB，相頻特性測試誤差約2°。

加噪聲后多諧差相信號測試法仿真的響應(yīng)信號如圖7所示，可見伺服機(jī)構(gòu)的響應(yīng)信號信噪比較低。

圖5 多諧差相信號測試法測得頻率特性及誤差曲線Fig.5 Frequency characteristic and error curve obtained by SPHS test method

多諧差相信號測試法測得的頻率特性曲線及其誤差曲線如圖8所示。由圖8可得，多諧差相信號測試法抗噪聲干擾能力弱，在噪聲干擾下的測試誤差較大，隨著頻率的增加，系統(tǒng)響應(yīng)幅值減小，噪聲占很大比重，測試誤差在較大范圍內(nèi)波動(dòng)。

3.3 濾波效果分析

多諧差相信號測試法受噪聲影響較大，需對采集信號進(jìn)行濾波處理。為保證濾除噪聲干擾的同時(shí)低頻響應(yīng)不被衰減，選擇巴特沃斯低通濾波器[15]。設(shè)置通帶截止頻率為20 Hz，通帶衰減為1 dB，阻帶截止頻率為100 Hz，阻帶衰減為50 dB，可得巴特沃斯低通濾波器的階數(shù)為4，歸一化截止頻率為0.05。

在同等噪聲條件下使用多諧差相信號測試法進(jìn)行仿真，應(yīng)用巴特沃斯低通濾波器對采集信號進(jìn)行濾波，得到濾波后的響應(yīng)信號如圖9所示。與圖7相比，響應(yīng)信號中的噪聲已經(jīng)基本濾除。

濾波前后測得頻率特性及其誤差曲線如圖10所示。由圖10可得，濾波前最大幅頻特性測試誤差約10dB，最大相頻特性測試誤差約45°，濾波后最大幅頻特性測試誤差約1.2 dB，最大相頻特性測試誤差約3°。采用巴特沃斯低通濾波器能有效濾除測試過程中的噪聲干擾，顯著提高頻率特性的測試精度，測試誤差與正弦相關(guān)分析法的測試誤差相差不大，能夠替代正弦相關(guān)分析法進(jìn)行快速準(zhǔn)確的頻率特性測試。

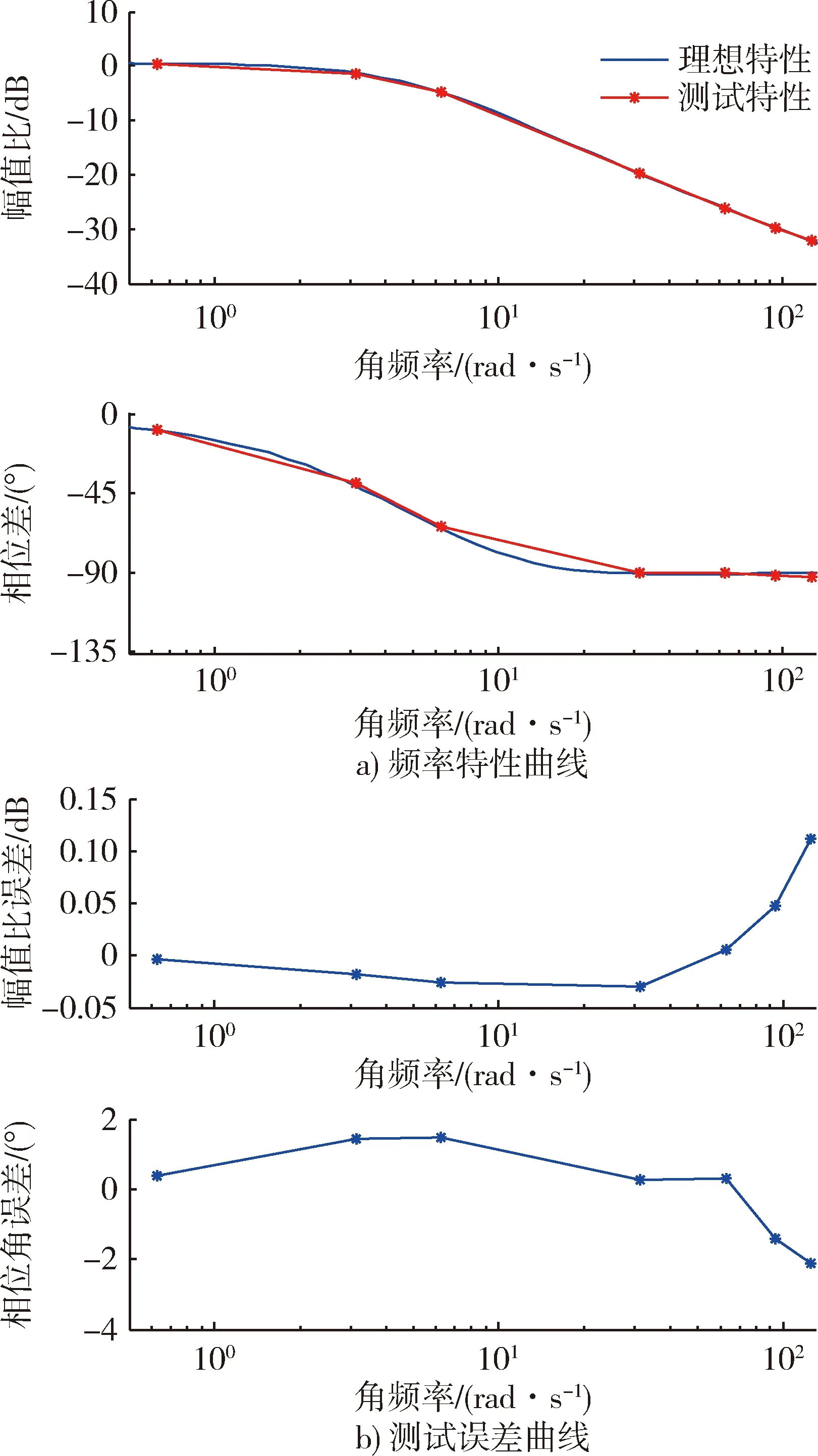
圖6 正弦相關(guān)分析法測得頻率特性及誤差曲線Fig.6 Frequency characteristic and error curve obtained by sinusoidal correlation analysis method

圖8 多諧差相信號測試法測得頻率特性及誤差曲線Fig.8 Frequency characteristic and error curve obtained by SPHS test method

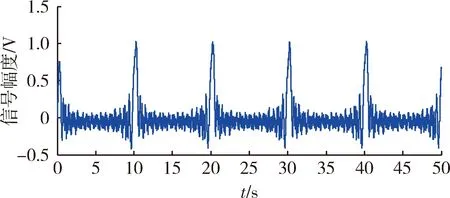
圖9 濾波后的響應(yīng)信號波形Fig.9 Waveform of filtered response signal

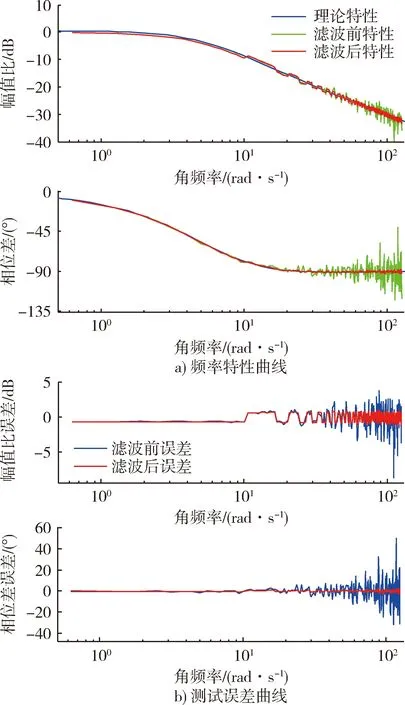
圖10 濾波前后測得的頻率特性及誤差曲線Fig.10 Frequency characteristic and error curve before and after filtering

4 結(jié)論

本文對多諧差相信號測試法進(jìn)行了改進(jìn)，并以某型導(dǎo)彈的伺服機(jī)構(gòu)為測試對象，分別在無噪聲和有噪聲的條件下使用傳統(tǒng)的正弦相關(guān)分析法和改進(jìn)的多諧差相信號測試法進(jìn)行仿真。主要結(jié)論如下：

(1) 無噪聲條件下，正弦相關(guān)分析法的幅頻特性測試精度更高，多諧差相信號測試法的相頻特性測試精度更高。相比之下，多諧差相信號測試法的測試速度更快，測試效率更高。

(2) 同等噪聲條件下，正弦相關(guān)分析法的抗干擾能力更強(qiáng)，多諧差相信號測試法需要對采集信號進(jìn)行濾波處理。

(3) 對多諧差相信號測試法采用巴特沃斯低通濾波能夠有效濾除測試中的噪聲干擾，顯著提高了測試精度，可以替代正弦相關(guān)分析法進(jìn)行快速準(zhǔn)確地頻率特性測試。