懸鏈線方程的推導與應用

張華杰 易洪榮 王豪 梁吉雷

摘? 要：文章主要研究懸鏈線的一般形態(tài)問題，基于對懸鏈線的受力分析，給出了懸鏈線一般方程與標準方程的推導過程。針對適用于海洋工程系泊系統(tǒng)的錨鏈設計，構建了近海觀測網(wǎng)在不同情況下的數(shù)學模型，展示如何利用迭代算法和約束條件，求解近海錨鏈形態(tài)。

關鍵詞：懸鏈線方程;受力分析;迭代算法

中圖分類號：U662? ? ? ? ?文獻標志碼：A? ? ? ? 文章編號：2095-2945（2019）26-0173-04

Abstract： This paper mainly studies the general morphology of catenary. Based on the force analysis of catenary， the derivation process of general equation and standard equation of catenary is given. Aiming at the anchor chain design suitable for marine engineering mooring system， this paper constructs the mathematical model of offshore observation network under different conditions， and shows how to use iterative algorithm and constraint conditions to solve the shape of offshore anchor chain.

Keywords： catenary equation; force analysis; iterative algorithm

現(xiàn)實生活中存在各種各樣的曲線，懸鏈線就是其中的一種。懸鏈線是一種常用曲線，物理上用于描繪懸在水平兩點間的因均勻引力作用下的軟繩的形狀，因此而得名（圖1）。

1 懸鏈線方程的推導

為方便受力分析，本文先討論懸掛點等高時，即相鄰懸掛點無高差時鐵鏈的受力情況。根據(jù)對稱性，本文取一半的鐵鏈進行分析，如下：

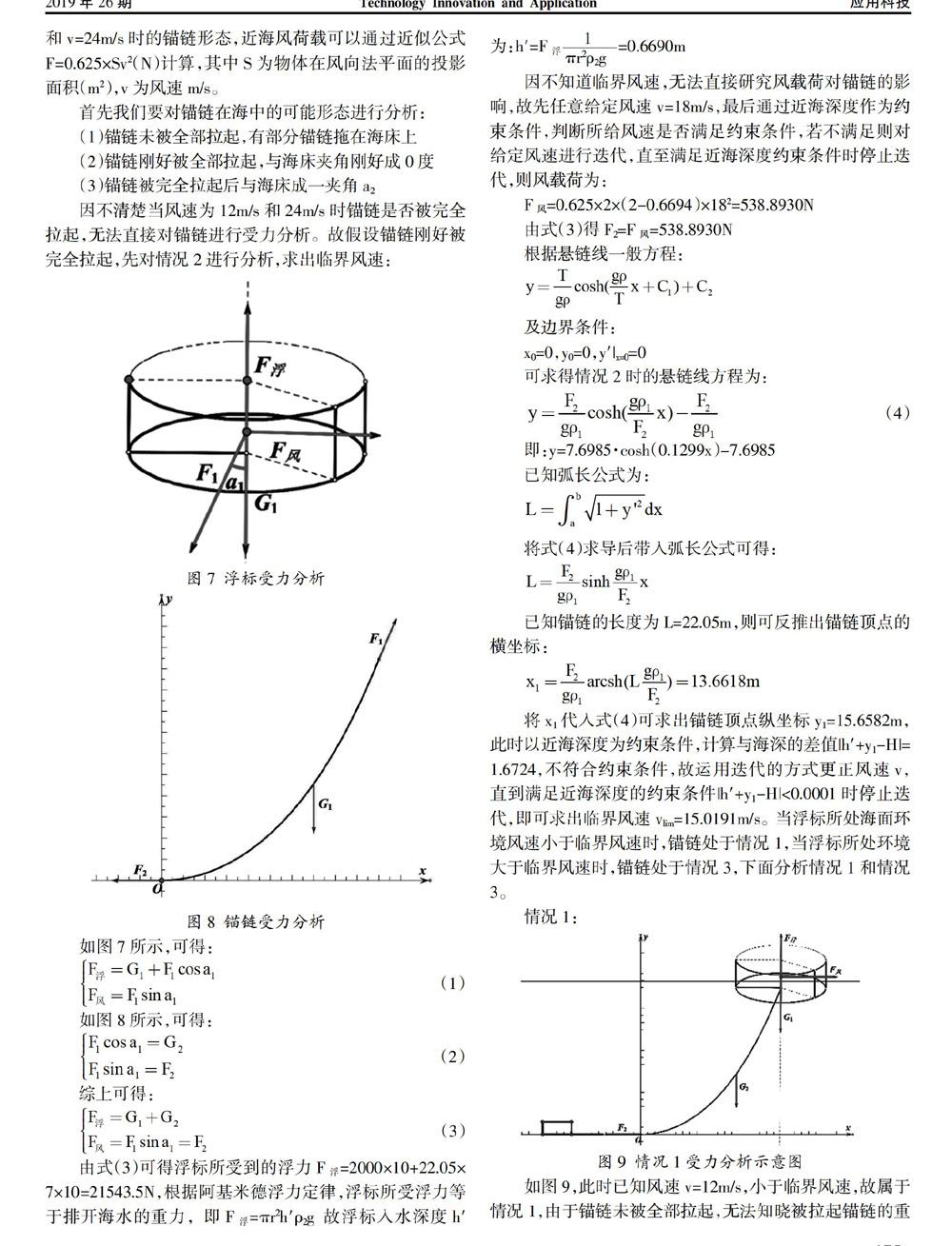
本文以等高懸掛著的鐵鏈（以下稱為懸鏈）的最低點為原點建立如圖2所示的直角坐標系，同時假定懸鏈與兩端懸掛點均在同一平面內，懸鏈為連續(xù)質量均稱可均勻形變的柔鏈。故可將懸鏈設為y=f（x），設點A為鐵鏈上任意一點（x，y），懸鏈OA段分別受到A點沿切線方向往上的拉力F，自身所受重力G以及最低點水平向左的拉力T，將受力關系放入一個三角形中可得（圖3）：

因懸鏈處于靜止狀態(tài)，由靜力學平衡條件可知懸鏈OA段各方向上的分解受力必然平衡，即：

如圖6所示，近淺海觀測網(wǎng)系統(tǒng)由浮標和系泊系統(tǒng)組成。某型傳輸節(jié)點的浮標系統(tǒng)可以簡化為重為m1=2000kg高為h=2m底面半徑為r=1m的圓柱體，錨鏈長L=22.05m單位質量為ρ1=7kg/m。現(xiàn)將該型近海觀測系統(tǒng)布放在水深為H=18m，且海床平坦、海水密度為ρ2=1.025×103kg/m3的海域中。若此時海水靜止，分別研究海面風速為v=12m/s和v=24m/s時的錨鏈形態(tài)，近海風荷載可以通過近似公式F=0.625×Sv2（N）計算，其中S為物體在風向法平面的投影面積（m2），v為風速m/s。

首先我們要對錨鏈在海中的可能形態(tài)進行分析：

（1）錨鏈未被全部拉起，有部分錨鏈拖在海床上

（2）錨鏈剛好被全部拉起，與海床夾角剛好成0度

（3）錨鏈被完全拉起后與海床成一夾角a2

因不清楚當風速為12m/s和24m/s時錨鏈是否被完全拉起，無法直接對錨鏈進行受力分析。故假設錨鏈剛好被完全拉起，先對情況2進行分析，求出臨界風速：

3 結束語

本文主要對懸鏈線方程進行推導與研究，給出了懸鏈線方程的一般表達式，演示如何使用約束條件和迭代算法解決近海錨鏈的形態(tài)問題。因主要討論錨鏈形態(tài)而簡化了模型，忽略海水流力等其它因素對浮標的影響，故在實際設計分析時應對其他影響因素逐層分析討論，不可一味忽略。目前近海系泊系統(tǒng)的設計與優(yōu)化為我國近海觀察檢測提供了實用的理論，對近海船舶作業(yè)具有重要意義，是我國現(xiàn)今熱門的研究方向，而未來研究方向則需更多地考慮海中多種因素對錨鏈影響以及錨鏈材料的選擇問題。

參考文獻：

[1]劉崢銳.懸鏈線方程在近海單點系泊系統(tǒng)設計中的應用[J].內蒙古科技與經(jīng)濟，2017，11：120-122.

[2]何英豪，朱雨薇，韓冰凌.基于懸鏈線方程的系泊系統(tǒng)分析[J].工業(yè)設計，2016，11：136-137.

[3]胡靈斌，唐軍.懸鏈線方程的求解及其應用[J].船舶，2004，1：17-20.