VSP測井資料在合成地震記錄制作中的應用研究

張建華

(中國石化勝利油田分公司 勘探開發研究院,山東 東營 257015)

地震解釋首先要進行層位標定,確定地震反射層位和地質層位之間的關系。目前最常用的層位標定方法是合成地震記錄標定。合成地震記錄制作過程中需要對波阻抗曲線進行時深轉換,時深轉換一般采用的方法是對聲波測井曲線進行簡單的積分[1]。這樣制作的合成地震記錄在與井旁地震道進行對比時,需要依據標志層的對比分析進行整體的漂移,但在標志層對準的情況下,經常會存在其他的地震反射同相軸無法對準問題。筆者對利用聲波測井資料計算時深關系的原理進行深入分析,闡明產生這種現象的原因,并研究利用VSP測井資料的時深關系對波阻抗曲線進行時深轉換,進而制作合成地震記錄的方法,并對其效果進行對比分析。

1 合成地震記錄基本原理

合成地震記錄可以看作是一種一維的地震模型正演,即認為地層界面是水平的,射線在界面上是正入射的,射線路徑是垂直的。這種近似盡管忽略了地震響應隨入射角的變化效應,但在通常情況下是合理的。當入射角確實對地震響應的影響較大時,必須使用近炮檢距部分地震道集疊加而不是全部疊加,來與合成地震記錄進行對比。合成地震記錄的制作通常可以分計算波阻抗曲線、對波阻抗曲線進行時深轉換、計算反射系數曲線、將反射系數序列與子波褶積生成合成地震記錄4個步驟:

(1)計算波阻抗曲線。波阻抗是地層密度和縱波速度的乘積,分別可以由密度測井資料和聲波測井資料得到。如果缺少密度測井資料,考慮到密度的變化遠遠小于縱波速度的變化,因此可以近似地假定密度不變,即以速度曲線代替波阻抗曲線來計算反射系數,所產生的誤差一般情況下可以忽略。也可以利用加德納(Gardner)公式由聲波測井資料近似計算得到密度。

ρ=0.31v0.25.

(1)

式中,ρ為密度,g/cm3;v為縱波速度,m/s。

如果缺少聲波測井資料,可以利用法斯特(Faust)公式由電阻率測井資料近似計算得到縱波速度,因為巖層速度和巖層電阻率都隨巖石孔隙度增加而變小。這個公式的適用范圍是深度大于200～300 m,自然電位曲線上沒有特殊的峰值,而且地層水的礦化度變化很小。

v=KH1/6R1/6.

(2)

式中,H為深度,m;R為電阻率,Ω·m;K為一個與巖石性質有關的常數。

(2)對波阻抗曲線進行時深轉換。將以深度為函數的波阻抗曲線轉化為以雙程旅行時為函數的波阻抗曲線。這就需要知道井的時深關系。通常情況下,通過對聲波測井曲線進行簡單的積分來得到時深關系[2]。

(3)

式中,tH為深度H對應的旅行時,μs;τ(h)為聲波時差曲線,μs/m。

(3)計算反射系數曲線。反射系數是地震波垂直入射時,反射振幅與入射振幅的比值。地下第n個地層界面處縱波的零炮檢距反射系數由如下公式算出:

Rn=(An+1-An)/(An+1+An).

(4)

式中,Rn為地下第n個地層界面的反射系數,無量綱;An和An+1分別是第n個界面上下兩個地層的波阻抗,kg/(m2·s)。

(4)將反射系數序列與子波進行褶積生成合成地震記錄。地震子波的選取通常有兩種方法,一種方法是使用理論子波,如雷克子波,另一種方法是從地震數據中提取子波。

f(t)=S(t)*R(t).

(5)

式中,f(t)為合成地震記錄,S(t)為地震子波,R(t)為反射系數。

2 利用聲波測井資料進行時深轉換存在問題

在上述合成地震記錄制作的第2個步驟中,通常通過對聲波測井曲線進行簡單積分得到時深關系,進而對波阻抗曲線進行時深轉換。實際計算時,可以采取一種比較簡單的方法實現(3)式的計算:假設某口井的聲波測井曲線起始深度為d1,在深度上有d1、d2、d3、…、dn-1、dn共計n個采樣點,可以認為它們將地層分成了c1、c2、…、cn-1共計n-1層(圖1),把每一層當成是均質的,且認為它們的速度分別為1/τ2、1/τ3、…、1/τn,則每一層的雙程旅行時分別為2(d2-d1)τ2、2(d3-d2)τ3、…、2(dn-dn-1)τn,這樣某一深度點所對應的雙程旅行時即為其上各層雙程旅行時的總和,即

(6)

式中,tn為深度dn對應的雙程旅行時,μs;dk、dk-1為聲波測井第k個、第k-1個采樣點對應的深度,m;τk為深度dk對應的聲波時差,μs/m。

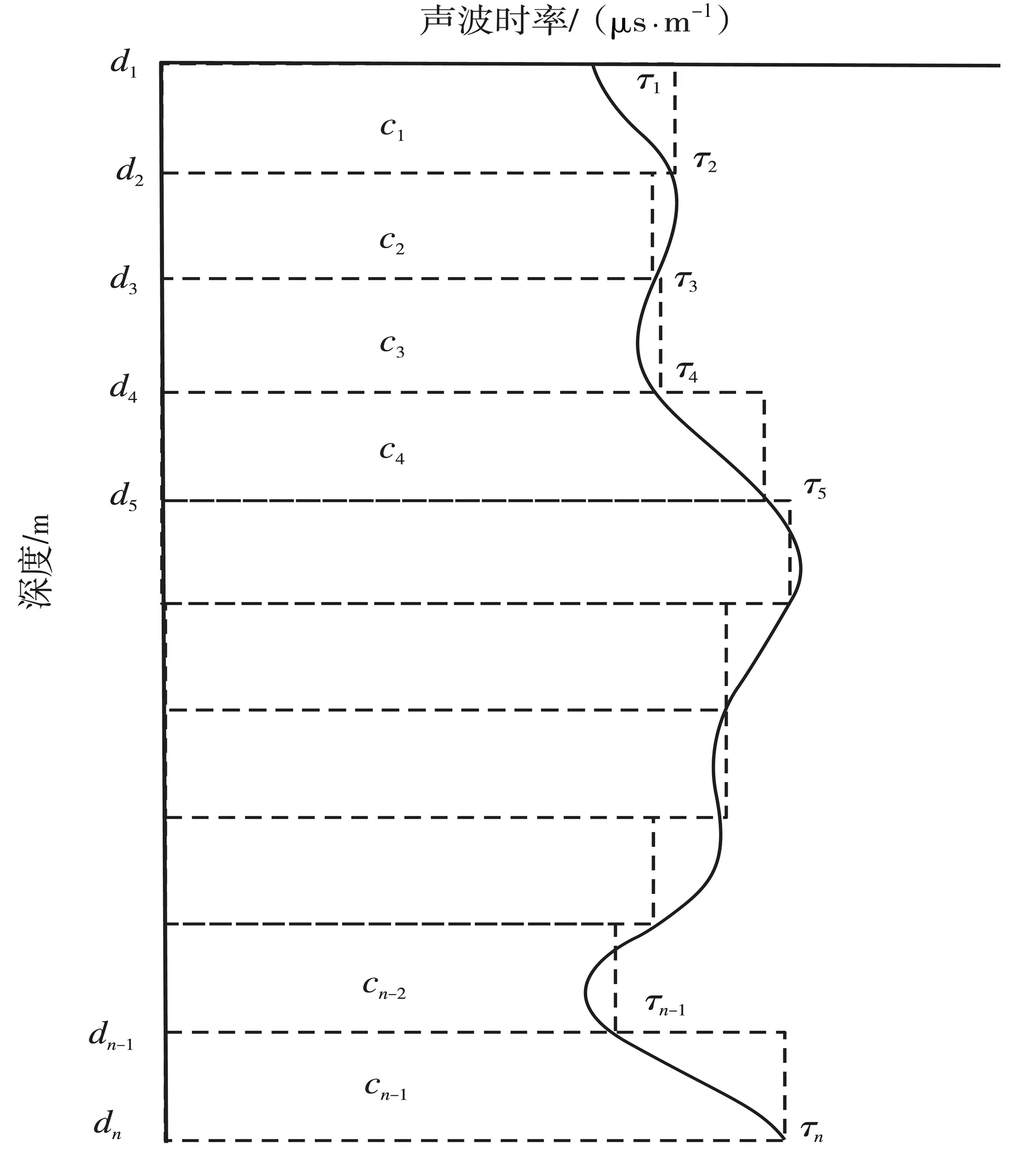
圖1 利用聲波時差計算時深關系的方法

由式(6)即可較為方便得到井點的時深關系,但是它存在以下兩方面的問題:

(1)式(6)計算的雙程旅行時是地下某一深度到測井起始深度d1的雙程旅行時,而地震數據的雙程旅行時是地下某一深度到地震基準面的雙程旅行時。如圖2所示,要得到地下某一深度到地震基準面的雙程旅行時,需要將地下某一深度到測井起始深度的雙程旅行時加上測井起始深度至地震基準面之間的雙程旅行時T0。T0由兩部分組成,一部分是地震基準面至地表的雙程旅行時T01,可以由地震基準面與地表的高程差和替換速度求得;另一部分是地表至測井起始深度的雙程旅行時T02,由于缺少這一深度段的聲波時差數據,T02無法直接求取。這樣,由于缺少井的最淺部的聲波時差測井數據而使得T0難以直接的準確求取,從而無法直接得到基于地震基準面的時深關系[3]。所以一般情況下制作的合成地震記錄無法直接與井旁地震道進行對比分析。

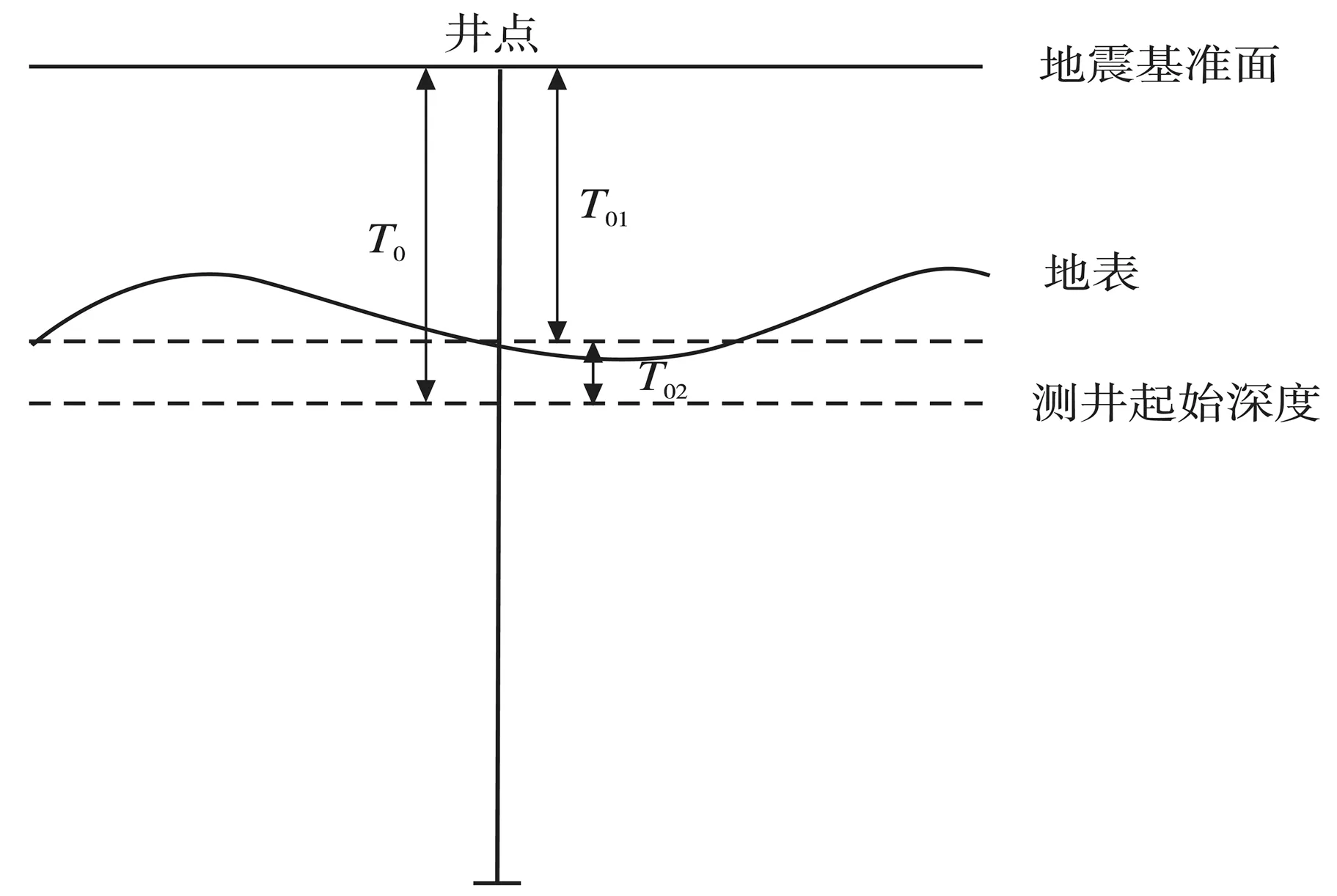
圖2 T0求取示意圖

對于T0難以直接準確求取這個問題,可以采用標志層對比的方法來解決。通過分析井點的速度特征,選取一個明顯的速度界面作為標志層,在地震剖面上找到該標志層對應的反射同相軸,地震剖面上該標志層對應的時間值與聲波時差計算出的該標志層對應的時間值之差即為T0[4-5]。這樣,根據標志層的對比分析,對合成地震記錄進行整體的漂移,就可以得到井點基于地震基準面的時深關系,以上就是利用合成地震記錄標定得到基于地震基準面的時深關系及平均速度的原理。

(2)聲波時差曲線本身的誤差會使計算的時深關系不準確。聲波時差曲線受井徑、地層厚度、“周波跳躍”現象的影響,可能無法準確反映地層的時差值[6],進而由聲波時差計算得到的時深關系的精度也受到影響。這樣,在進行合成地震記錄對比時,雖然標志層通過整體漂移實現了準確的對應(圖3中反1 250～1 325 ms處的3個強軸),但其他的某些射同相軸還是會對不準(圖3中725和875 ms處的強軸)。這時需要對合成地震記錄進行局部的拉伸或壓縮,使其他的反射同相軸也能準確對應。

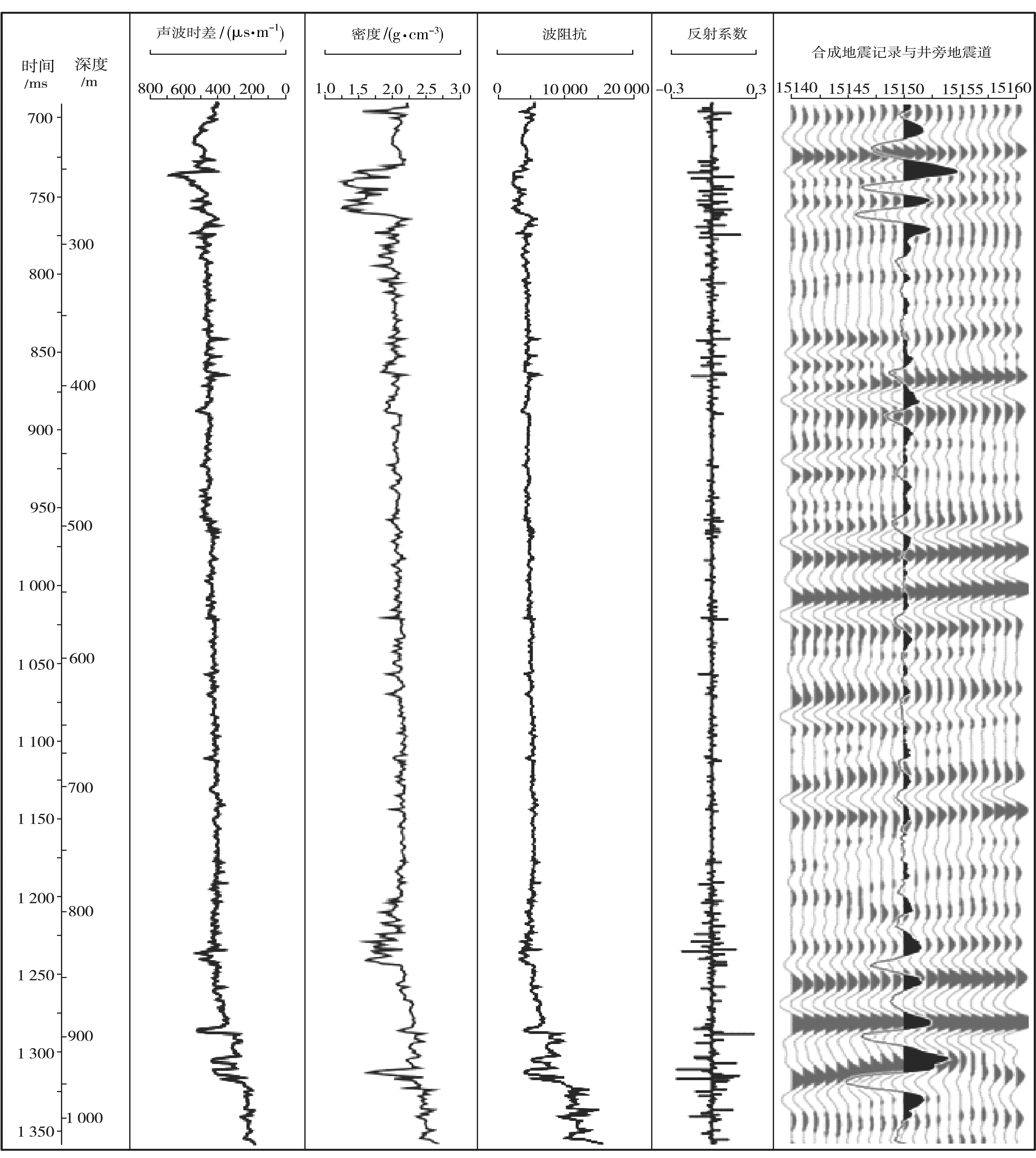
圖3 利用聲波時差數據進行時深轉換的合成地震記錄標定

但這種局部拉伸壓縮的方法不能濫用,不能通過這種局部拉伸壓縮的方法將合成地震記錄上所有的同相軸都與井旁地震道的同相軸一一對準。因為合成地震記錄和實際地震道中都有可能存在不可靠的同相軸。聲波時差的誤差不只影響時深關系,還影響波阻抗、反射系數的計算,從而影響合成地震記錄中某些同相軸的可靠性。井旁地震反射中也會出現多次波等不能真實反映地層界面的同相軸。除此之外,還有一些其他的原因,如地震采集處理過程中的某些因素等[7],使得合成地震記錄中的同相軸無法與實際地震道中的同相軸完全一一對應。

3 利用VSP時深關系進行時深轉換

如果在合成地震記錄制作時,該口井有VSP測井資料,利用VSP測井提供的時深關系代替由聲波時差計算的時深關系對波阻抗曲線進行時深轉換會取得更好的對應效果。VSP測井是將測井檢波器放入井中,記錄下從井口至井下各深度處直達波的傳播時間,通過井口地表海拔與地震基準面的高程差和替換速度即可換算出地震基準面至井下各深度處的雙程旅行時,不存在像聲波測井那樣淺部無法獲取數據的問題,又由于時間值是直接讀得的,因此時深關系誤差較小。因此,VSP測井是地震與測井信息之間建立聯系的最佳方法。圖4是利用VSP時深關系進行時深轉換得到的合成地震記錄,與圖3相比,首先不需要進行整體的漂移,1 250～1 325 ms處的標志層(3個強軸)對應的比較準確;其次,不需要進行局部的拉伸壓縮,其他的反射同相軸(725 ms和875 ms處的強軸)就有較好的對應關系。

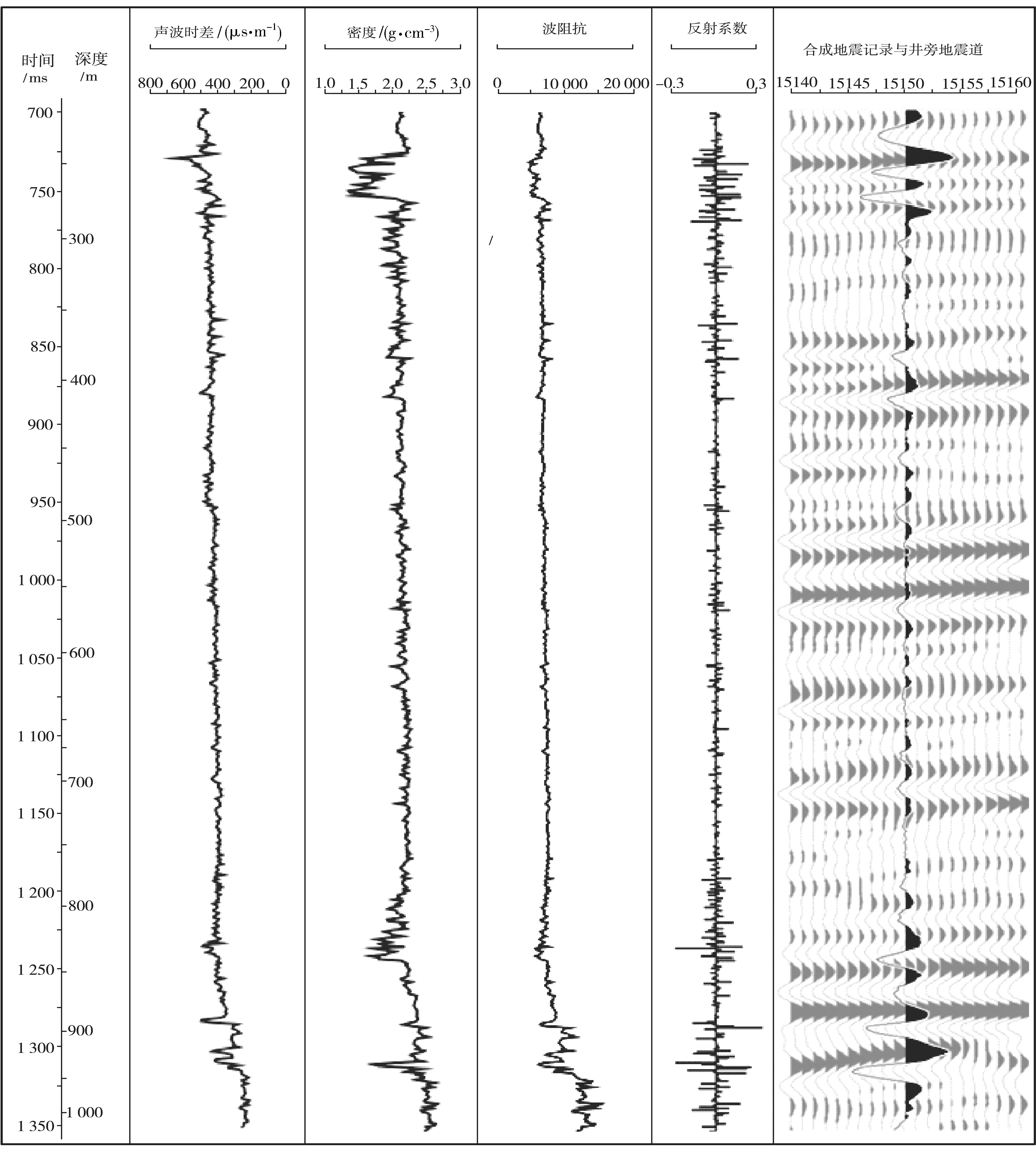
圖4 利用VSP時深關系進行時深轉換的合成地震記錄

對比利用聲波時差計算的時深關系和VSP時深關系也可以看出,在1 250～1 325 ms標志層處兩者較為吻合,越向淺部兩者的差別越大。

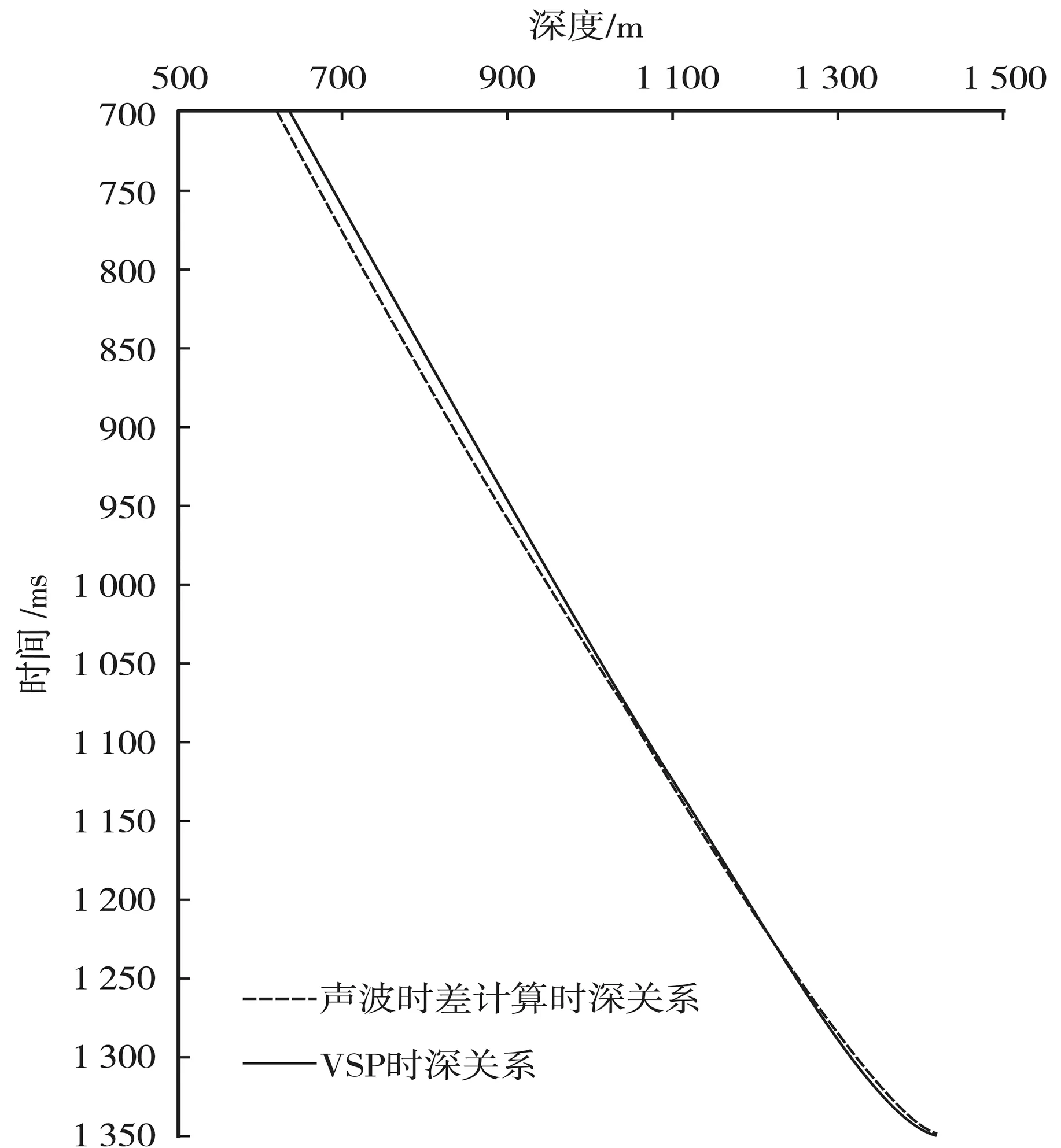
圖5 聲波時差計算的時深關系與VSP時深關系對比

4 結 論

在合成地震記錄的制作過程中需要將波阻抗曲線由深度域轉換到時間域。通常利用聲波時差測井數據計算時深關系來進行這種時深轉換。但由于井的淺部缺少聲波時差數據,無法直接得到基于地震基準面的時深關系,同時聲波時差曲線本身存在誤差,會使計算的時深關系不準確。而由VSP測井資料得到的時深關系不存在像聲波測井那樣淺部無法獲取數據的問題,又由于VSP測井測量的井口至井下各深度處直達波的傳播時間值是直接讀得的,時深關系誤差較小。因此,利用VSP時深關系對波阻抗曲線進行時深轉換制作的合成地震記錄不需要進行整體的漂移,也不需要進行局部的拉伸和壓縮,便可以實現與井旁地震道的標志層和大部分反射同相軸較好的對應。