納米流體液膜蒸發自組裝雙尺度沉積結構三維模擬*

高超 袁俊杰 曹進軍 楊薈楠 單彥廣

(上海理工大學能源與動力工程學院,上海市動力工程多相流動與傳熱重點實驗室,上海 200093)

納米流體液膜在自然狀態下蒸發干燥后除了形成單一尺度的網狀連續結構、枝狀分形結構以及微尺寸環結構等沉積結構,還會形成雙尺度細胞網絡沉積結構和雙尺度納米粒子環狀沉積結構.為了更直觀地研究納米流體液膜雙尺度沉積結構的形成機理,本文在二維動力學蒙特卡羅模型的基礎上,建立了三維動力學蒙特卡羅模型,并加入了耦合溶劑蒸發率的動態化學勢,成功模擬出了雙尺度細胞網絡沉積結構和雙尺度納米粒子環狀沉積結構,并討論了動態化學勢中化學勢銳度與流體臨界蒸發率對納米流體液膜蒸發自組裝雙尺度沉積結構的影響.模擬結果與文獻中的實驗結果吻合良好.

1 引 言

近年來納米流體在微納制造、信息技術、生物醫學等領域得到了廣泛的應用[1-6].除了強化傳熱方面的研究外,納米流體的蒸發干燥及沉積結構的理論研究和應用也日益受到關注[7-11].納米流體在自然蒸發時,懸浮在流體中的納米粒子會受到運動阻力、布朗力、粒子間作用力、重力等作用力[2,4,5,12-15]的影響,運動規律極其復雜.當納米粒子從基液中沉積到基板上時,可以自發地形成各種各樣的沉積結構.這些沉積結構包括蠕蟲狀結構、網絡狀連續結構、樹枝狀分形結構以及微尺寸的環結構等[14-26].通過理論模擬預測納米流體蒸發后形成的沉積結構,有助于揭示納米流體蒸發自組裝機理并推動調控自組裝過程方法的發展.

2003年,Rabani等[16]在二維伊辛模型[17]的基礎上通過系統化學勢得出的系統能量變化建立了適用于納米流體蒸發干燥及沉積結構的二維動力學蒙特卡羅(kinetic Monte Carlo,KMC)仿真模型,能夠再現納米粒子的自組裝模式,得到了和實驗相符合的結果,從而開創了使用KMC方法模擬納米流體蒸發干燥及沉積結構模擬的研究.Crivoi和Duan[18]在二維KMC方法的基礎上對開放邊界納米流體液膜進行了模擬研究.Zhang等[19]則使用了隨時間和位置變化的函數來表達液體的有效化學勢,從而使二維KMC方法可以用于模擬納米流體液滴的蒸發沉積過程.Martin等[20]則對含有鈍化金納米粒子的納米流體液膜的沉積結構進行了實驗研究,并與利用KMC方法模擬的結果進行了比較分析,發現馬蘭戈尼對流并不是網狀沉積結構形成的必要條件.之后,Stannard和Martin等[21,22]通過實驗發現納米流體液膜的沉積結構具有雙尺度現象,即沉積結構中較大尺度與較小尺度的沉積結構同時出現,并均勻地交錯在一起.這種沉積結構在以往的KMC方法模擬結果中從未出現.因此Stannard和Martin等[21]建立了耦合溶劑蒸發率的動態化學勢函數用于研究雙尺度沉積結構的形成機理.

上述利用KMC方法對納米流體液膜蒸發沉積過程的研究均采用二維假定.而實際納米流體液膜通常存在一定的厚度,因此應考慮蒸發沉積時不同層納米流體化學勢的分布和變化,以及納米顆粒之間的相互作用.為此,近年來發展了基于不同厚度預測液膜蒸發的三維模型,并用于預測網狀連續結構及枝狀分形結構等沉積結構[23,27-29].對于Stannard等實驗發現的納米流體液膜蒸發沉積的雙尺度結構,目前尚未見采用分層定義動態化學勢的三維模型的研究報道.本文在Rabani等[16]提出的二維KMC模型的基礎上建立了三維KMC模型,并將模型劃分為多層結構,加入了耦合溶劑蒸發率的動態化學勢函數[21],分別為三維模型的每一層液膜定義了不同的動態化學勢,使之隨著每層液膜溶劑蒸發率的變化而變化,更貼近于液膜真實蒸發情況,以此模擬納米粒子的雙尺度沉積結構,并討論了化學勢銳度與流體臨界蒸發率對納米流體液膜自然蒸發雙尺度沉積結構的影響.

2 模型及化學勢函數

2.1 模型及假定

本文建立的三維納米流體液膜模型如圖1所示.圖中仿真區域邊長為1024 × 1024個格子,紅色格子代表納米粒子,藍色格子代表液體,綠色格子代表基板,所有模擬結果圖尺寸均為1024 × 1024.本文建立的納米流體液膜計算域是厚度為4層的納米流體液膜層(根據計算能力和模擬需要,格子數和層數理論上可無限擴充),第一層為基板層,第二層為與下層基板和上層液膜接觸的液膜底層,第三層為與上下兩層液膜接觸的液膜中間層,第四層為與下層液膜和上方空氣接觸的液膜頂層,納米流體液膜的所有狀態與變化都可由這四層表示.本文對三維納米流體液膜的蒸發過程做出如下假設:

1)納米流體液膜的厚度足夠小,不考慮對流且忽略液膜的曲率變化,并假設納米粒子在液膜內均勻分布;

2)干燥過程屬于自然蒸發,液膜外部環境保持不變;

3)納米流體液膜自然蒸發過程中粒子的移動主要由液體蒸發驅動[16,25].

基于以上假設,本文采用KMC模型對三維納米流體液膜的蒸發與沉積過程進行模擬.

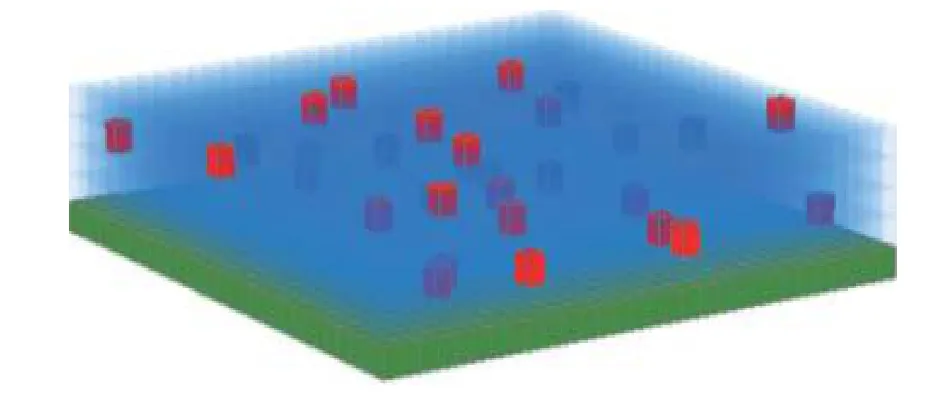
圖1 納米流體液膜的物理模型圖Fig.1.Physical model of 3D nanofluid thin-film.

2.2 KMC模型

本文建立的三維KMC模型是由二維KMC模型發展而來[16],主要通過計算整個系統的能量變化來確定液膜中的液體是否蒸發、氣體是否冷凝以及納米粒子是否移動.在KMC模型的具體計算過程中,納米粒子的具體尺寸對模擬結果的影響不大,并非關鍵參數[16],計算時假設一個納米粒子占據一個格子; 模型中的基板體現為具有固體特性的1024 × 1024個格子,且與納米粒子狀態相同,不涉及基板具體材料對沉積結構的影響.模型中共存在三種不同的狀態: 氣態、液態、固態(基板和納米粒子),而模型中的每一個格子只能存在一種狀態.在此模型中采用三個相應參數,用以表現任意格子的狀態: l,n,s.具體表示如下: l=0,n=0(氣體); l=1,n=0 (液體); l=0,n=1 (納米粒子); s表示基板.

計算開始后,首先將液體填充進計算域內的所有格子,然后根據模型預先設定的粒子濃度,將相應數量的納米粒子隨機地分布在由液體格子組成的液膜中,液膜四周邊界采用封閉區域邊界處理,即邊界處狀態與納米粒子相同.開始蒙特卡羅計算時,每一次計算都包括三部分嘗試: 首先嘗試改變每一個液體格子的狀態,使其狀態變為氣體,即蒸發過程; 然后嘗試改變每一個氣體格子的狀態,使其狀態變為液體,即冷凝過程; 最后進行N次嘗試,使每一個納米粒子朝著一個隨機方向移動,N為粒子在液體中的擴散率.這里的每一次嘗試是否成功都由Metropolis概率(Pacc)所決定[16]:

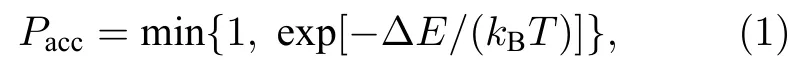
式中ΔE是格子狀態改變前后系統哈密頓量(Hamiltonian)的變化值,kB是玻爾茲曼常數,T是溫度,Pacc是模擬計算中每一次嘗試是否成功的概率.將Pacc和系統隨機生成的值進行比較,大于隨機值則嘗試成功,如果小于隨機值則嘗試失敗,即格子狀態不會改變,并開始下一次嘗試.在模型中,由于粒子移動主要是由液體的蒸發推動,所以納米粒子只能移動到液體格子區域,并與液體格子交換位置來保持溶劑密度不變.而當納米粒子周圍沒有液體時,納米粒子便無法移動.當計算域中沒有液體時,則模擬結束.

模擬中采用的三維KMC模型通過計算整個系統的能量漲落來判斷納米流體中的蒸發、冷凝和粒子的移動.系統的總能量由哈密頓量(E)來表示[25],

式中εnn,εnl,εll分別表示相鄰納米粒子之間的相互作用能、相鄰納米粒子和純組分液體之間的相互作用能、相鄰純組分液體之間的相互作用能.在進行三維KMC方法計算時,將納米粒子和基板之間的相互作用能和納米粒子與納米粒子之間的相互作用能大小取值一致.除此之外,所有的相互作用能都是純組分液體相互作用能εll的倍數,在本文中定義 εnn=2εll,εnl=1.5εll,在整個模擬計算過程中,基板的狀態始終恒定.如圖2所示,在系統能量計算時,需要計算與中心計算點接觸的6個一級接觸點和12個二級接觸點,由于有距離衰減,所以在計算二級接觸點的作用力時要乘以加權值

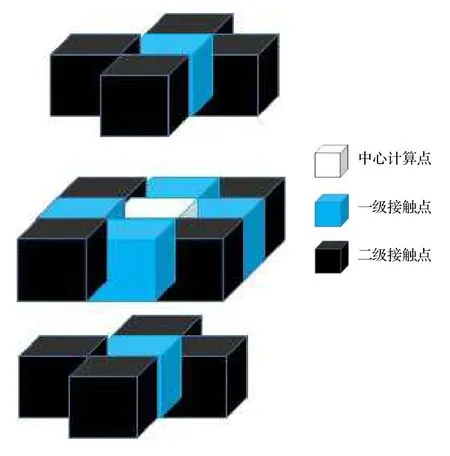
圖2 接觸點示意圖Fig.2.Schematic diagram of contact points.

2.3 動態化學勢函數

在KMC模型中,液體的蒸發主要由液體的化學勢和系統的內能兩部分決定[18].基于本文之前的假設,三維納米流體液膜在蒸發過程保持恒溫狀態,其內部溫度不會因為蒸發散熱而改變,所以系統的內能在蒸發進行過程中保持恒定,因此在蒸發過程中液體的蒸發主要由系統的化學勢決定.二維模型中封閉納米流體液膜在化學勢的處理上將其看作定值[11,14,16,20,22],所以沉積結構單一.本文所采用的化學勢函數中耦合了溶劑蒸發率,使之成為了動態化學勢,并分別為模型中的每一層液膜定義了不同的動態化學勢,使之更貼近于液膜真實蒸發情況.動態化學勢函數為[21]

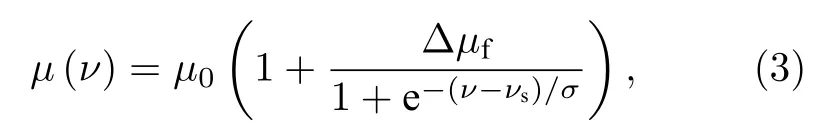
其中ν是溶劑蒸發率,νs是溶劑的臨界蒸發率,μ0是系統的初始化學勢,Δμf是化學勢銳度,表示化學勢突變的劇烈程度,變化幅度為初始化學勢的相應倍數,σ是無量綱常數,本文取σ=0.01.由(3)式可知,化學勢函數中間會發生一次突變,產生前后兩個不同的化學勢值,因此模擬前后會有兩個不同的蒸發速率.本文將此動態化學勢應用到三維模型中來預測納米流體液膜自然蒸發形成的雙尺度沉積結構.

2.4 模型驗證

2.4.1 液膜各層蒸發狀態

圖3中的模型參數為: ?=16%,kBT=0.20,μ0=—3.65,N=30,Δμf=0.15,νs=55%,σ=0.01,其表示的是納米流體液膜在200—1000蒙特卡羅步數(MCS)時各層的蒸發狀態,? 為納米粒子濃度.圖3(a)—(e)是頂層液膜,圖3(f)—(j)是中間層液膜,圖3(k)—(o)是底層液膜.如圖所示,灰色區域為純組分液體,黑色區域為納米粒子,白色區域為蒸汽.在封閉邊界的三維納米流體液膜蒸發時,首先會隨機在頂層蒸發成核,但并不是頂層完全蒸發干燥后才進行下面各層的蒸發,而是先蒸發形成孔洞,然后孔洞區域向四周和下方擴大,直到各層蒸發率達到臨界蒸發率時各層的化學勢分別發生突變,液膜內的液體迅速蒸發,納米粒子則在基板層沉積,圖3(c)和圖3(d)便是頂層液膜化學勢突變后液體迅速蒸發的結果.在蒸發過程中,上層的納米粒子會隨著液體的蒸發而下移,下層的納米粒子則會隨著上層的兩相接觸線的擴大而后退.隨著上層流體的蒸發,納米粒子會在下一層接觸空氣的兩相接觸線處聚集.因為每一層都有納米粒子,所以沉積結構中三相線這部分為重合結構,重合的多少和納米粒子的濃度有關.在圖3(e)、圖3(j)與圖3(o)中可以看出,最上層和中間層的沉積附著在底層沉積結構上,形成最終的沉積結構,因此,本文后面的模擬結果均直接采用底層沉積結構表示.

圖3 三維納米流體液膜各層蒸發圖Fig.3.Evaporation diagram of each layer of 3D nanofluid thin-film.

2.4.2 模擬與實驗對比

圖4是納米流體液膜蒸發的實驗與模擬對比圖.圖4(a)是厚度為80 nm的聚苯乙烯(polystyrene)液膜在硅基板上的干燥去濕實驗過程[31],圖4(b)是納米粒子濃度 ?=12%的納米流體液膜蒸發干燥模擬過程,其中kBT=0.20,μ0=3.775,N=30,Δμf=0.15,νs=95%,σ=0.01.對比圖4(a)與圖4(b)可知模擬與實驗過程一致,結果吻合良好,由此驗證了本文模型的可靠性.

3 結果與討論

3.1 雙尺度結構模擬

圖5(a)和圖5(b)分別為采用動態化學勢得到的雙尺度細胞網絡狀沉積結構模擬結果和實驗結果[21]的對比.圖5(a)顯示了使用動態化學勢后液膜蒸發沉積的模擬結果,其中kBT=0.20,μ0=3.75,N=30,Δμf=0.15,νs=55%,σ=0.01,?=12%,圖5(b)是尺寸為2 nm的金納米粒子與辛硫醇組成的濃度為1 mg/mL的納米流體液膜干燥后5 μm2大小的原子顯微鏡(TM-AFM)圖,模擬結果和實驗結果之間的對應性很強.由圖5(b)可知,圖中的大尺度細胞網絡結構占主導地位,而小尺度的沉積結構則出現在大尺度細胞網絡之間.模擬開始時,在整個薄膜的隨機位置發生慢熱成核,薄膜中的孔隨后逐漸生長形成大尺度細胞網絡結構.然而,隨著溶劑的蒸發率ν接近臨界蒸發率νs,化學勢μ會出現跳躍式增加,這時蒸發系統不穩定,會在極短的時間內在液膜剩下的液體區域中形成許多小孔,然后迅速干燥直至完全沉積,形成小尺度網狀甚至是點狀沉積結構,與大尺度細胞網絡結構一起構成雙尺度沉積結構.

圖4 實驗結果與模擬結果對比 (a)實驗結果[31]; (b)模擬結果Fig.4.Comparison between experimental and simulation results: (a)Experimental results[31]; (b)simulation results.

圖5 雙尺度細胞網絡結構模擬結果與實驗結果對比(a)模擬結果; (b)實驗結果[21]Fig.5.Comparison of simulation and experimental of dualscale cellular network structure: (a)Simulation result;(b)experimental result[21].

圖6 雙尺度納米粒子環狀結構模擬結果與實驗結果對比 (a)模擬結果; (b)實驗結果[21]Fig.6.Comparison of simulation and experimental of dualscale nano-rings structure: (a)Simulation result; (b)experimental result[21].

圖6(a)和圖6(b)分別是雙尺度納米粒子沉積環結構的模擬結果與實驗結果[21]的對比.其中圖6(a)模擬參數如下: kBT=0.22,μ0=3.60,N=30,Δμf=0.15,νs=0.09,σ=0.01,?=15%; 圖6(b)是大尺度納米粒子沉積環結構與小尺度沉積結構共存的1 μm2TM-AFM圖像,圖像由尺寸為2 nm的金納米粒子與辛硫醇組成的濃度為1 mg/mL的納米流體液膜干燥后所得.對比圖6(a)和圖6(b)可以發現,模擬結果與實驗結果吻合良好.從實驗與模擬圖中可以看出存在兩種不同類型的沉積結構,這表明蒸發過程中存在兩種不同的干燥模式,即化學勢突變前的緩慢干燥模式與化學勢突變后的迅速干燥模式.利用加入模型中的動態化學勢可以成功地模擬這兩種干燥模式.

3.2 化學勢銳度對沉積結構的影響

圖7是在不同化學勢銳度下蒸發結束后三維納米流體液膜的沉積結構,其中 ?=12%,μ0=—3.75,kBT=0.20,N=30,νs=55%,σ=0.01.圖7(a)—(f)的化學勢銳度 Δμf分別為 0,0.050,0.100,0.125,0.150,0.200.在蒸發過程中溶劑蒸發率達到臨界蒸發率之后,化學勢會發生突變,突變后的化學勢大小是由化學勢的銳度大小決定的,化學勢的銳度越大,化學勢突變之后和原來的差別就越大,而前后化學勢的差別大小決定了雙尺度沉積結構的差別狀況.從圖7(a)—(c)中可以看出,在相同初始化學勢時,化學勢銳度在一定范圍內會對突變之后的沉積結構產生影響.當化學勢銳度為零時,化學勢不會發生突變,沉積結構與使用恒定化學勢時出現的單尺度沉積結構相同; 當化學勢銳度較小時,大尺度網狀沉積結構與密集的小尺度網狀沉積結構共存; 隨著化學勢銳度的增大,大尺度沉積結構保持不變,而密集的小尺度網狀結構進一步變小,變為點狀沉積結構.從圖7(d)—(f)中可以看出,當化學勢銳度超過一定值時,化學勢銳度對沉積結構的影響會逐漸變小,最終雙尺度沉積結構保持不變.

圖7 不同化學勢銳度下封閉納米流體液膜的沉積結構圖 (a)Δμf=0; (b)Δμf=0.050; (c)Δμf=0.100; (d)Δμf=0.125; (e)Δμf=0.150; (f)Δμf=0.200Fig.7.Sedimentary pattern of nanofluid thin-film at different chemical potential sharpness: (a)Δμf=0; (b)Δμf=0.050; (c)Δμf=0.100; (d)Δμf=0.125; (e)Δμf=0.150; (f)Δμf=0.200.

3.3 流體臨界蒸發率對沉積結構的影響

圖8是在不同流體臨界蒸發率下蒸發結束后三維納米流體液膜的沉積結構,其中 ?=12%,μ0=—3.75,kBT=0.20,N=30,Δμf=0.150,σ=0.01.圖8(a)—(f)的流體臨界蒸發率νs分別為1%,10%,30%,55%,80%,100%.在其他參數不變時,臨界蒸發率主要決定兩種沉積結構的面積占比.如圖8(a)所示,當流體臨界蒸發率較小時,化學勢在蒸發初期就發生突變,突變后的化學勢絕對值較大,導致液體迅速蒸發,納米粒子會直接沉積在基板上形成線條狀或點狀沉積結構,所以圖8(a)全是小尺度沉積結構.圖8(b)、圖8(c)與圖8(d)分別是化學勢在蒸發前期、中期與后期發生突變的結果,其中大尺度沉積結構逐漸增多,小尺度沉積結構則逐漸減少.由圖8(e)與圖8(f)可知,當臨界蒸發率很大時,納米粒子在化學勢突變前有足夠的時間隨著三相線的移動而聚集在不同三相接觸線的匯聚處,并沉積在基板上形成與采用恒定化學勢時獲得的單尺度網狀沉積相同的結構.

圖8 不同臨界蒸發率下封閉納米流體液膜的沉積結構圖 (a)νs=1%; (b)νs=10%; (c)νs=30%; (d)νs=55%; (e)νs=80%;(f)νs=100%Fig.8.Sedimentary pattern of nanofluid thin-film at different critical evaporation rates: (a)νs=1%; (b)νs=10%; (c)νs=30%;(d)νs=55%; (e)νs=80%; (f)νs=100%.

4 結 論

1)在二維KMC模型的基礎上建立了三維KMC模型,并加入了耦合溶劑蒸發率的動態化學勢,成功模擬出了雙尺度細胞網絡沉積結構和雙尺度納米粒子環狀沉積結構,模擬結果與實驗研究的結果吻合良好.

2)化學勢銳度是決定雙尺度沉積結構的主要參數,銳度為零時,沉積結構表現為單尺度分布;隨著化學勢銳度的增加,沉積結構向雙尺度分布演變.

3)流體臨界蒸發率決定了雙尺度沉積結構中兩種不同沉積結構的面積占比,隨著流體臨界蒸發率的增大,小尺度沉積結構的占比逐漸減少,大尺度沉積結構的占比逐漸增加,直至全部變為大尺度沉積結構.