基于分裂格式有限點集法對孤立波二維非線性問題的模擬*

任金蓮 任恒飛 陸偉剛 蔣濤

(揚州大學,數學科學學院,水利與能源動力學院,揚州 225002)

在提出一種基于時間分裂格式的純無網格有限點集(split-step finite pointset method,SS-FPM)法的基礎上,數值模擬了含孤立波的二維非線性薛定諤 (nonlinear Schr?dinger,NLS)/ (Gross-Pitaevskii,GP)方程.SS-FPM的構造過程為: 1)基于時間分裂的思想將非線性薛定諤方程分成線性導數項和非線性項; 2)采用基于Taylor展開和加權最小二乘法的有限點集法,借助Wendland權函數,對線性導數項進行數值離散.隨后,模擬了帶有Dirichlet和周期性邊界條件的NLS方程,將所得結果與解析解做對比.數值結果表明: 給出的SS-FPM粒子法的優點是在粒子分布非均勻情況下仍具有近似二階精度,且較網格類有限差分算法實施容易,較已有改進的光滑粒子動力學方法計算誤差小.最后,運用SS-FPM對無解析解的二維周期性邊界NLS方程和Dirichlet邊界玻色-愛因斯坦凝聚二分量GP方程進行了數值預測,并與其他數值結果進行對比,準確展現了非線性孤立波奇異性現象和量子化渦旋過程.

1 引 言

含孤立波解的非線性問題常見于非線性光學和晶體的熱脈沖物理現象[1-3],以及玻色-愛因斯坦凝聚態 (BEC)動力學特性[3-6]中.該非線性物理現象的研究通常會涉及非線性薛定諤(nonlinear Schr?dinger,NLS)方程或 (Gross-Pitaevskii,GP)方程的求解[5-7],然而NLS/GP方程中含有的非線性項或旋轉角動量算子使得多分量或高維情況下的孤立波形解難以用解析手段精確地得到[7,8].目前已提出了多種數值方法對NLSE/GPE進行求解或對復雜孤立波傳播過程進行預測,如有限元法[9]、有限差分法[10,11]、蒙特卡羅法[12,13]、修正的歐拉算法[14]、時間分裂譜方法[11,15]和基于背景網格無網格方法[16-18]等.然而上述基于網格的方法在多維復雜區域或非均勻節點分布情況下編程模擬實現都較復雜.近些年來,純無網格方法(粒子方法)以其完全不依賴于網格的優勢在實數域偏微分方程的模擬中得到了許多應用,如光滑粒子動力學方法(smoothed particle hydrodynamics,SPH)方法[19-23]和有限點集法 (finite pointset method,FPM)[24-26]等.但上述純無網格方法對復數域上含孤立波解非線性問題的模擬研究還處于起步階段,特別是FPM方法對非線性薛定諤方程的模擬在國際上還鮮有研究.

不依賴于背景網格的FPM方法具有粒子方法的特點,其在非線性薛定諤方程的模擬應用上還處于試探性研究階段,這與其在數值穩定和數值精度方面還待進一步研究相關.FPM方法精度和穩定性的提高,以及非線性薛定諤方程的數值模擬研究均是國際上的兩個研究熱點.FPM方法模擬復雜非線性薛定諤方程較網格類方法的主要優點在于: 可以任意布點,不受區域復雜性限制; 計算空間導數可采用二階精度顯格式且不依賴于網格; 模擬程序易于實現且便于并行實施.

本文針對非線性薛定諤方程的特點,為提高直接推廣FPM方法模擬帶非線性項問題的精度和穩定性,首先將非線性薛定諤方程進行時間分裂分為非線性項和線性導數項; 其次,引入Wendland權函數[26],采用基于Taylor展開和移動最小二乘思想的顯式FPM格式對線性導數部分進行離散;從而得到一種能夠準確、高效地求解非線性薛定諤方程的基于時間分裂有限點集法 (split-step finite pointset method,SS-FPM).所得數值結果表明,提出的SS-FPM能夠有效地求解帶有Dirichlet和周期性邊界條件的二維非線性薛定諤方程且具有二階精度,并能夠準確預測出周期邊界條件下孤立波變化奇異現象和Dirichlet邊界條件下帶外旋轉BEC二分量的孤立波值隨時間變化的量子化渦旋過程.

2 Gross-Pitaevskii方程

Gross-Pitaevskii方程常被用來描述量子力學中BEC動力學特性[1,11],本文考慮如下帶角動量旋轉項的無量綱化GP方程:

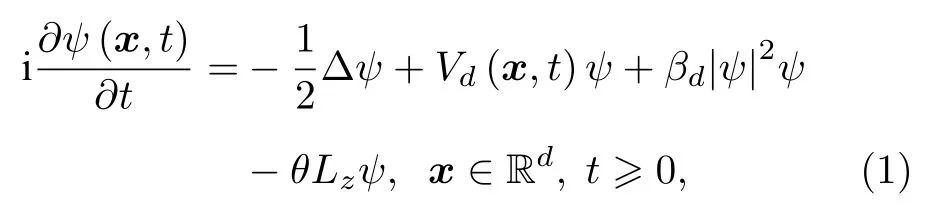
初值條件

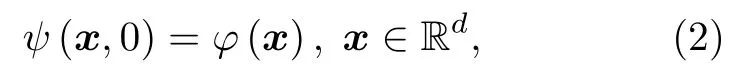
邊值條件

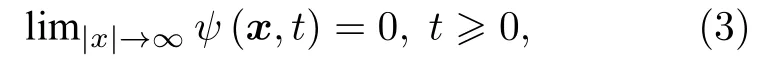
或周期邊值條件

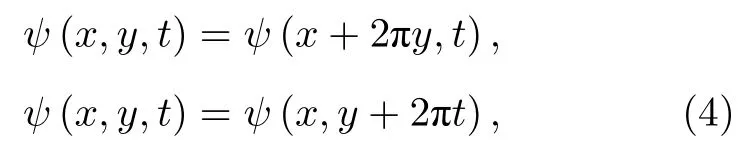
其中空間變量x=(x,y),或(x,y,z);ψ(x,t)是d維空間中的復值波函數;Δ是d維空間的拉普拉斯算子,是虛數單位;φ(x)是一個給定初值的復值函數.無量綱實數βd通常用來描述三次非線性項的相互強度|ψ|2ψ,Lz=-i(x?y-y?x)是無量綱旋轉角速度θ下的角動量算子的z分量,勢Vd(x,t)是一個實值函數,其形式為

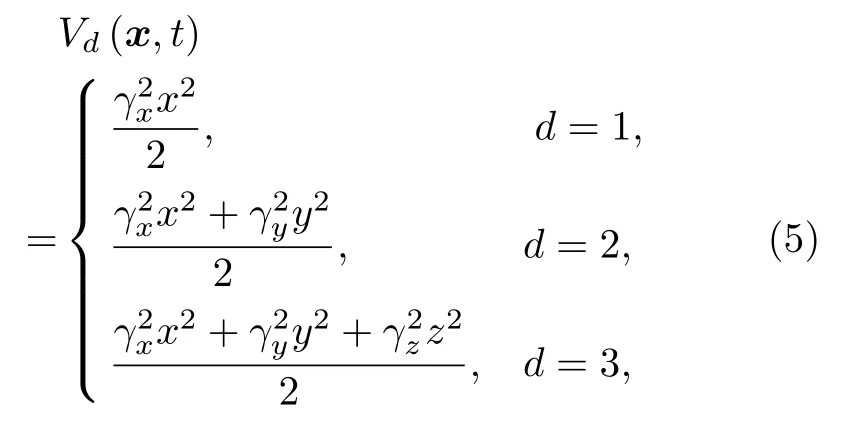
其中γx,γy,γz為實常數;Vd還可以是周期性的函數.

3 SS-FPM

本文針對超冷原子BEC動力學特性問題的粒子法模擬,將時間分裂格式與FPM進行耦合,得到能夠準確模擬GP方程的SS-FPM.本文提出的SS-FPM方法較直接拓展應用FPM方法[24,25]模擬GP方程具有較高精度和更好的長時間模擬穩定性,這是由于長時間模擬NLS/GP方程時,方程中的非線性項對算法精度和穩定性的要求較高.本文提出的SS-FPM方法的思想是: 首先,應用時間分裂法將方程分解成帶非線性和線性導數項的兩個方程; 其次,采用具有較好穩定性的Wendland權函數[23]拓展應用FPM法對帶線性導數方程進行二階顯格式離散; 最后,采用二階時間分裂偽譜法對兩個方程進行交替求解.

3.1 時間分裂格式

引入文獻[7,10,15]中時間分裂(time-split,TS)法,GP方程(1)可被寫為

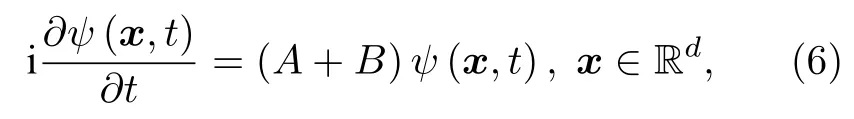
其中A=-(1/2)Δ-θLz是線性微分算子,B=Vd(x,t)+ βd|ψ(x,t)|2是非線性算子.于是上述方程可以被分解為如下的線性方程

和非線性方程

本文采用的二階分裂步法[7]: 首先求解(8)式,其次以(8)式的解作為初始條件求解(7)式,最后以(7)式的解作為初始條件求解(8)式,從而得到下一時間層的解.

3.2 FPM離散格式

對方程(7)的求解采用FPM法,時間上采用二階龍格-庫塔離散格式,函數導數項近似采用顯式FPM離散格式,FPM格式求解函數一階導數和二階導數的基本思想[24,25]是: 第一步,將求解域任意離散成有限點并賦初始值; 第二步,每個點x在權函數支持域內有相鄰粒子xj(j=1,2,···,n,n為支持域內相鄰粒子數),每個xj在x上進行Taylor展開并保留到二階導數項; 第三步,對Taylor級數余項進行整理,引入最小二乘法得到一個以x處一階/二階導數為未知函數的線性方程組; 第四步,求解涉及局部矩陣的線性方程組得到每個點x處函數導數近似值; 第五步,采用二階龍格-庫塔時間離散格式得到下一個時間層函數值.

本文以二維空間上均勻布點為例,采用具有較好穩定性Wendland權函數[23,27].Wendland權函數[23,27]形式如下:

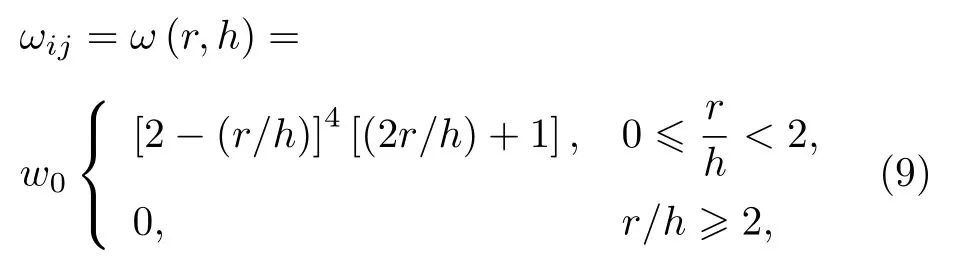
其中 r=|xj-x| 為 支持(域半)徑; ω0是一個正常數,ω0在二維空間中為 7 /64πh2,h為光滑長度,此處取 h ≈ 1.1λ0( λ0為分布粒子初始間距).

對任意點x處函數 ψ (x,t),其支持域內相鄰粒子為xj,函數 ψ (xj,t)在x點的Taylor級數展開

其中ej為Taylor級數展開時的余項誤差.將(10)式右端第一項放到等式左邊,則(10)式可以寫成

其中

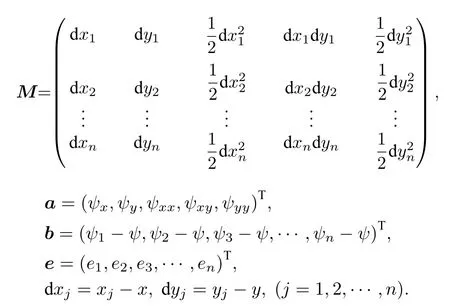
引入加權最小二乘法[24]可以得到

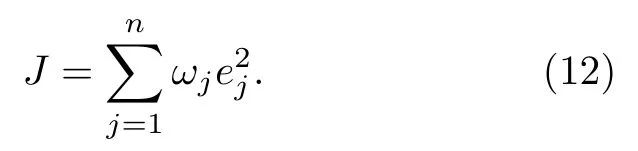
(12)式可以寫為

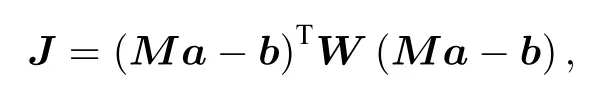
其中

根據極值原理,J取最小可得

通過(13)式包含5 × 5局部系數矩陣的線性方程組求解可得x處一、二階導數值.

3.3 SS-FPM離散格式

結合3.1節二階時間分裂格式與3.2節FPM離散格式,對GP方程(1)進行離散,可得如下SSFPM離散格式.

對非線性方程(8)通過求解常微分方程的方式進行求解[11],

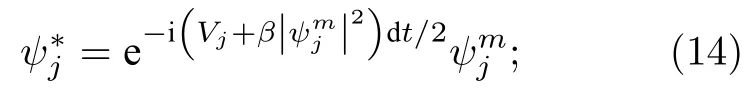
將(14)式求解得到的結果代入有限點集法中進行計算,再將求得的結果代入線性方程中,得到

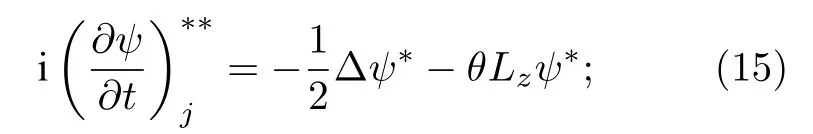
最后將方程(15)得到的解代入非線性方程(8)中進行求解,得到

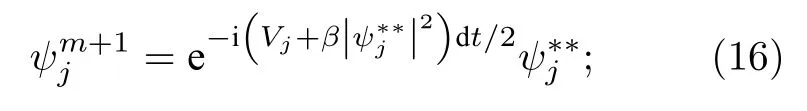
其中 j=0,1,2,···,N ,N是區域上離散化的粒子數; m=0,1,2,···為時間層;(15)式通過3.2節FPM離散格式進行求解得到

時間步長為dt,為保證數值模擬穩定性,時間步長的選擇通常需要滿足限制性條件 (見文獻[19,24,25]),本文選取為粒子初始間距).

初邊值條件施加:在 (14)式和(15)式計算中,初邊值條件的施加也是至關重要的,初始條件(2)式可以在計算 (14)式前進行準確施加=φ(x).邊值條件(3)式采用文獻[1,7,10]處理方式,將其近似為齊次Dirichlet邊值條件施加( ? Ω 為區域邊界).周期邊值條件(4)式的施加中為保證邊界上粒子的不足,采用SPH粒子方法的施加方式 (見文獻[19-21]),在物理量值更新前需要施加周期性條件的邊界上取大于等于支持域尺寸2h的粒子數及物理量賦到相對的邊界上.

4 NLS/GP方程SS-FPM模擬

為驗證提出的SS-FPM法模擬NLS方程的準確性和預測無解析解NLS/GP問題孤立波隨時間演化特性的可靠性,本節首先通過對帶兩種邊值條件的NLS方程的求解,與解析解做比較,對SSFPM法數值精度和收斂速度進行分析; 其次運用提出的粒子方法對周期邊界條件下孤立波奇異特性和BEC中孤立波量子化渦旋過程進行數值預測,并與其他數值結果(SS-FDM (split-step finite difference method)法[4,7]和SS-ICPSPH (split-step implicit corrected parallel smoothed particle hydrodynamics)法)[20]進行對比.為分析所提方法的精度和收斂性,本文定義如下誤差 (精確解與數值解最大誤差范數)和收斂階為:

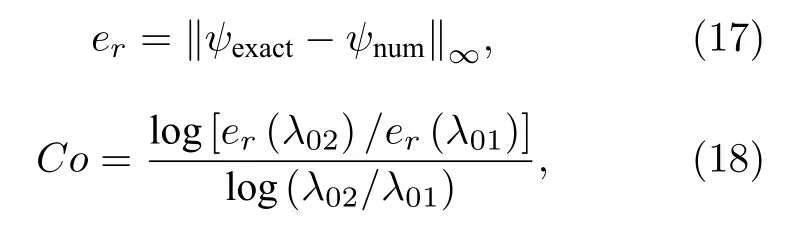
這里的 λ01和 λ02分別表示不同的粒子初始間距.

4.1 SS-FPM方法精度和收斂性分析

運用SS-FPM對兩個不同邊值條件下NLS方程進行求解,分析了所提方法模擬NLS方程的精度和收斂速度,討論了粒子分布非均勻情況下的數值誤差.

4.1.1 Dirichlet邊值NLS方程

考慮正方形區域 Ω :[0,2π]× [0,2π]的Dirichlet邊值條件的NLS方程[7,23],其對應的方程和初邊值條件分別為

其中V(x,y)=1-sin2xsin2y.

初值條件為

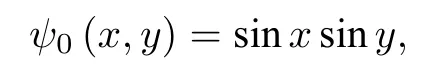
邊值條件為

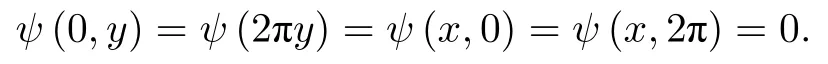
對應該問題的解析解為

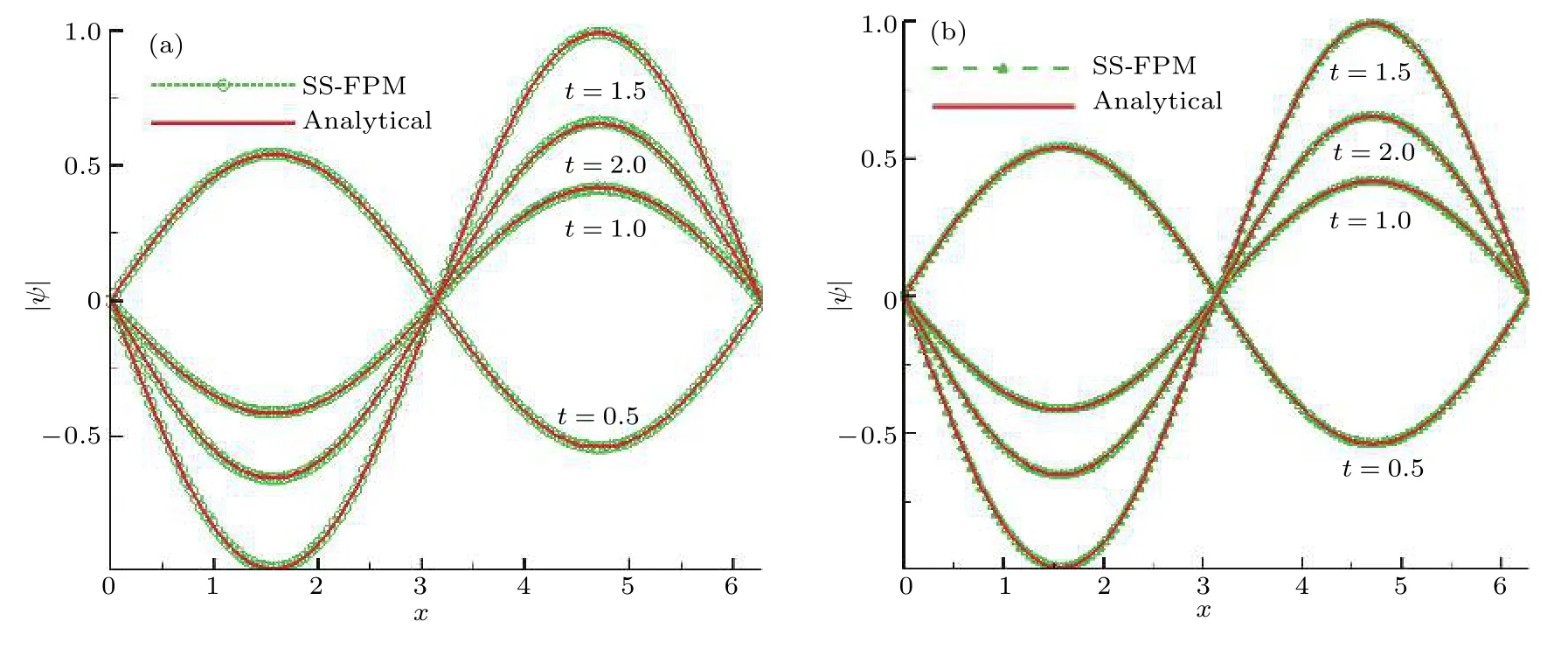
圖1 幾個不同時刻處沿 y=0.5π 的 | ψ| 變化曲線 (a)粒子均勻分布; (b)粒子非均勻分布Fig.1.The change curve of | ψ| along y=0.5π at different time: (a)Uniform mode; (b)non-uniform mode.

圖2 兩種不同的粒子分布 (a)均勻粒子分布; (b)非均勻粒子分布Fig.2.Two kinds of particle distribution: (a)Uniform mode; (b)non-uniform mode.

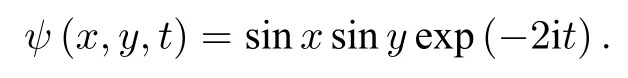
該算例模擬中采用粒子初始間距為 π /64 ,時間步長為dt=10—4.圖1給出了幾個時刻兩種粒子分布情況下SS-FPM法得到沿 y=0.5π 處波函數變化曲線,并與解析解進行對比.圖2展示了本算例模擬中采用的均勻和非均勻兩種粒子分布情況,其中圖2(a)的粒子是均勻分布方式,分別沿x,y方向每隔 π /64 的距離分布一個粒子; 圖2(b)中的粒子是非均勻分布方式,以 ( π,π)為圓心,靠近圓心第一層布6個粒子,第二層布12個粒子,逐步成等差數列方式向外擴展沿圓形分布粒子,相鄰兩個圓形層之間距離為相等均為 π /64 ,但邊界上仍采用均勻布點方式.由圖1可知,隨時間演化提出的粒子方法得到的波函數與解析解吻合,即使粒子分布非均勻下得到SS-FPM結果仍與解析解一致.

為進一步體現SS-FPM方法模擬Dirichlet邊值NLS方程的數值精度和收斂性,表1和表2分別給出了提出方法得到數值結果的誤差和收斂階.通過觀察表1,給出的粒子方法在粒子分布均勻和非均勻情況下得到的數值誤差差距不大,從而表明粒子方法模擬方程時無論區域是否規則都可以方便處理且具有較高的數值精度,較網格類方法具更好的靈活推廣應用性.由表2可知,SS-FPM法具有二階收斂速度,與文獻[23]中SS-ICPSPH法和文獻[7]中網格類SS-FDM法的收斂階基本一致,但本文提出的粒子方法得到的數值誤差較SSICPSPH法和SS-FDM法的誤差小.SS-FPM方法相較于直接采用FPM方法,前者具有較小誤差和較快的收斂速度,這是因SS-FPM方法對非線性薛定諤方程中非線性項采用了較準確的二階精度分裂格式.通過粒子法SS-FPM與網格類SS-FDM的構造過程以及粒子分布非均勻情況下圖2和表1結果可知,本文粒子方法不受網格限制,可以在模擬區域任意布點情況下對問題進行純無網格方法的模擬實現,較網格類方法具有更好的靈活應用推廣性,易被推廣應用于復雜非規則區域上薛定諤問題的模擬.

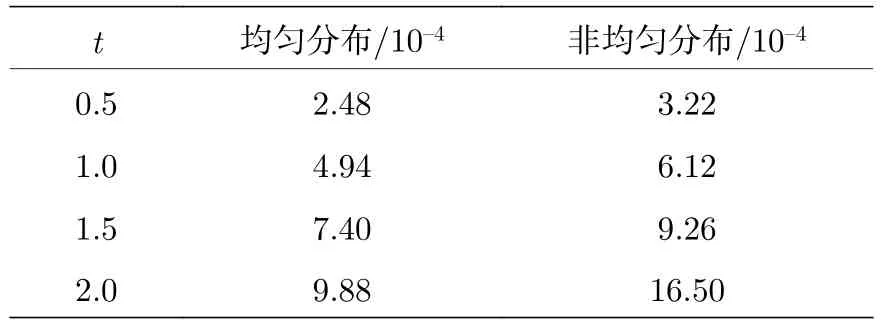
表1 粒子分布均勻/非均勻兩種情況下的最大誤差erTable 1.Maximum error er under uniform/nonuniform particles distribution.

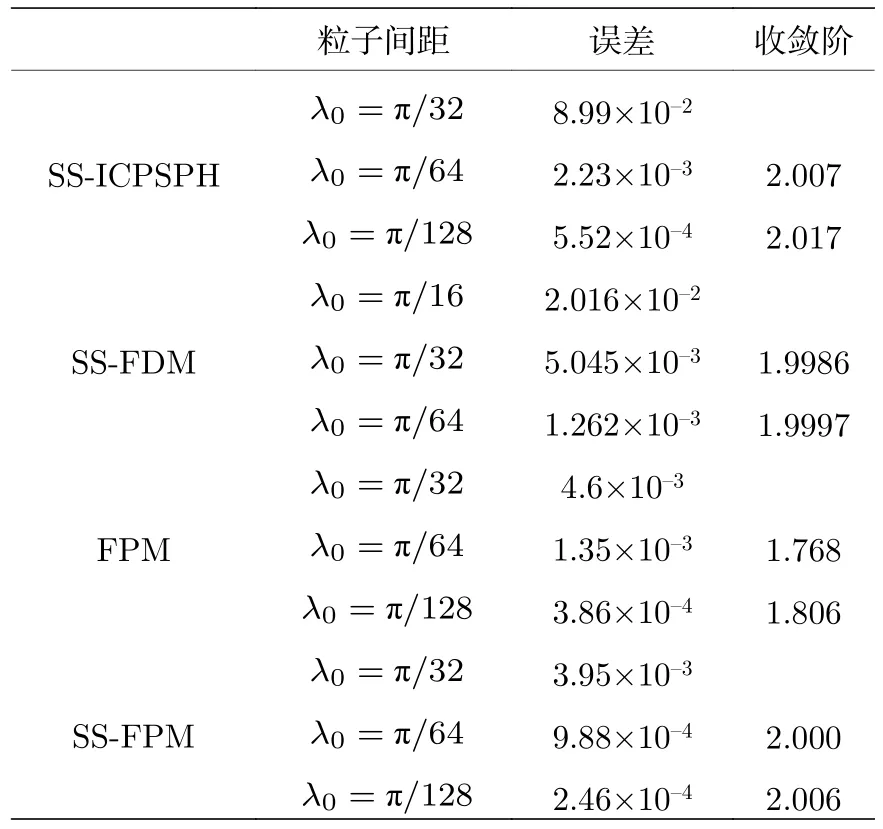
表2 四種不同方法在t=2時的數值收斂階Table 2.The rate of convergence obtained using four different methods at t=2.

4.1.2 周期邊值NLS方程

為體現提出的SS-FPM方法對帶周期性邊值NLS方程模擬的準確性,考慮正方形區域Ω:[0,2π]×[0,2π]的周期邊界條件的非線性薛定諤方程,其對應的方程和初值條件[11]為

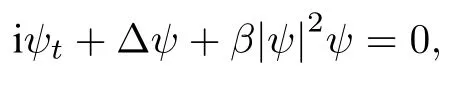
初值條件

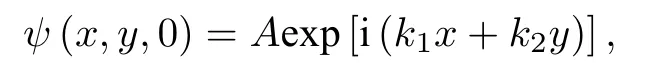
周期邊界條件

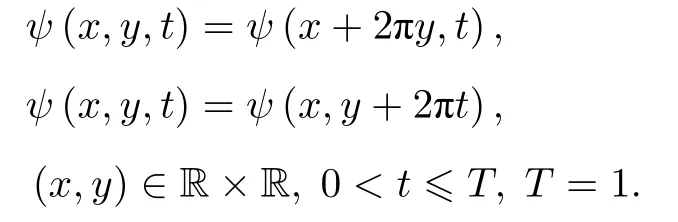
對應的解析解為

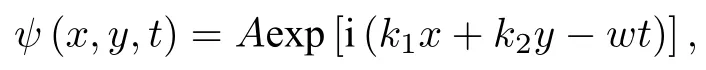
模擬中,選取 k1=k2=1 ,粒子初始間距 π /64 ,時間步長 d t=10-4.圖3給出了兩個不同位置、不同時刻SS-FPM法得到的波函數實部變化曲線,并與解析解進行比較.通過圖3可知,SS-FPM方法準確地展示了波函數實部隨時間演化呈現出的周期性波形,且數值結果與解析解吻合,從而表明提出的粒子方法可以準確地模擬帶周期邊值的NLS方程.表3給出了周期邊界條件下當t=2時刻三種不同方法的數值收斂階.由表3可知,本文提出的SS-FPM法與其他兩種數值方法收斂階接近,且較SS-ICPSPH方法誤差更小; 給出的SS-FPM法模擬周期邊界下非線性薛定諤問題具有二階收斂速度.

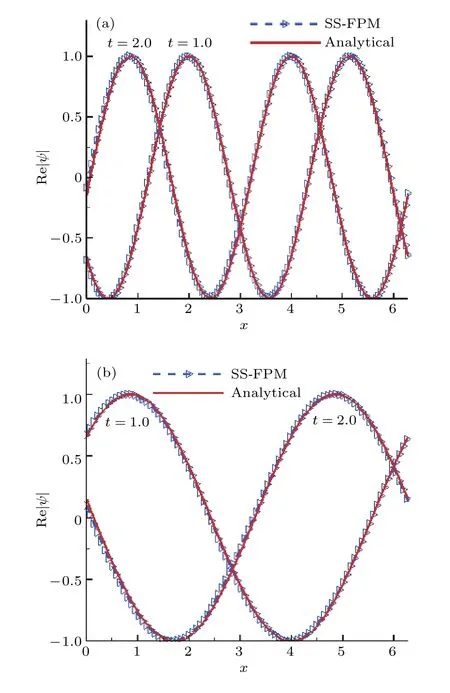
圖3 兩個不同位置不同時刻ψ實部變化曲線圖 (a)沿對角線; (b)沿y=πFig.3.The change curve of real part at two positions with different times: (a)Along the diagonal; (b)along y=π .

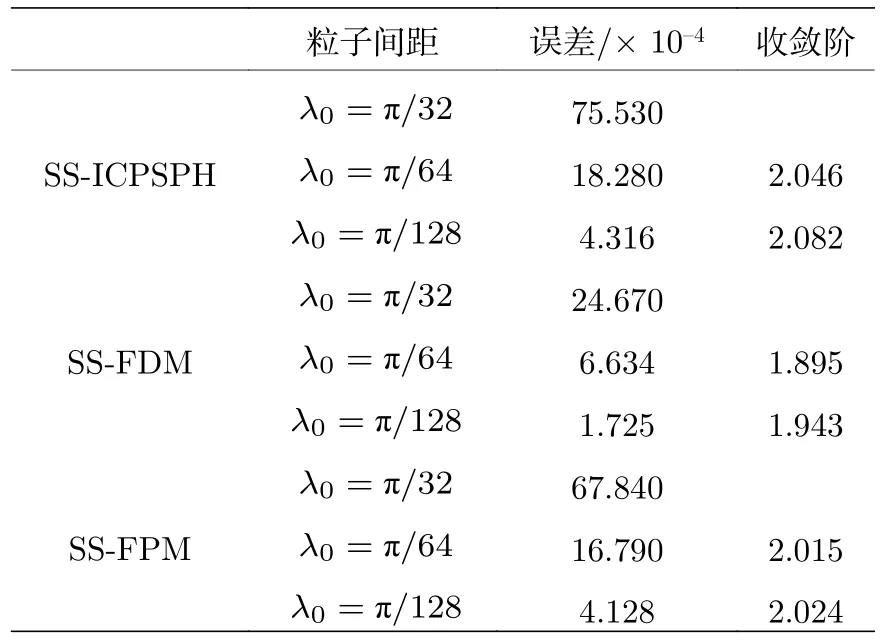
表3 三種不同方法在t=2時的數值收斂階Table 3.The rate of convergence obtained using three different particle methods at t=2.

4.2 數值模擬預測

為進一步體現SS-FPM方法模擬NLS/GP方程的能力,采用SS-FPM對帶周期邊界NLS方程中孤立波奇異特性和BEC中GP方程描述的孤立波量子化渦旋過程進行數值預測.

4.2.1 具有奇異性周期邊值NLS方程

考慮正方形區域 Ω :[0,2π]×[0,2π]的周期邊界條件的非線性薛定諤方程,其對應的方程和初值條件[11]為

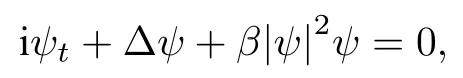
初值條件

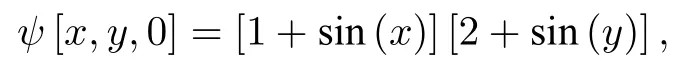
其中β=1.

該算例為無解析解的帶周期邊界NLS方程,它將描述隨時間演化孤立波出現奇異特性,常被用來驗證一種數值方法預測周期性NLS方程出現奇異值現象的可靠性和穩定性[11].本小節運用SSFPM粒子法對該算例進行了模擬,并與文獻[7]中SS-FDM法結果進行對比(見圖4).觀察圖4知,SS-FPM方法得到的帶周期邊界NLS方程的奇異值與SS-FDM結果吻合,表明提出的粒子方法模擬預測NLS方程描述的奇異特性是可靠的.

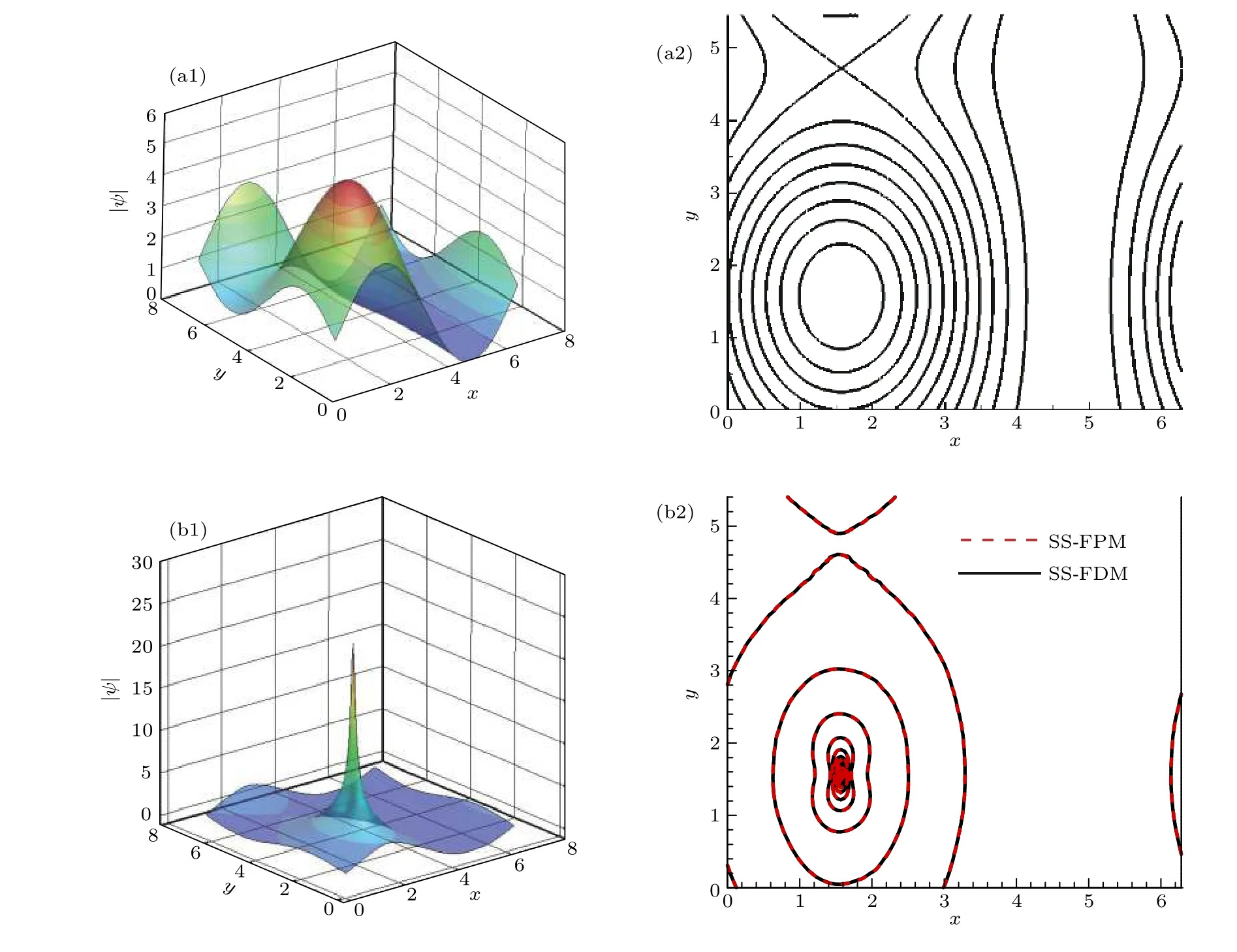
圖4 兩個不同時刻波函數 | ψ| 三維圖和等值線圖 (a1),(a2)t=0; (b1),(b2)t=0.0108Fig.4.The 3D graphs and contour of | ψ| at two different times: (a1),(a2)t=0; (b1),(b2)t=0.0108.

4.2.2 BEC中角動量旋轉GP方程

為驗證SS-FPM方法預測GP方程描述BEC動力學特性的有效性,考慮如下二分量帶旋轉項GP方程,并與其他數值結果進行比較.正方形區域 Ω :[-8,8]×[-8,8]上具有二分量角動量旋轉GP方程,及其對應的初邊值條件[8]為:

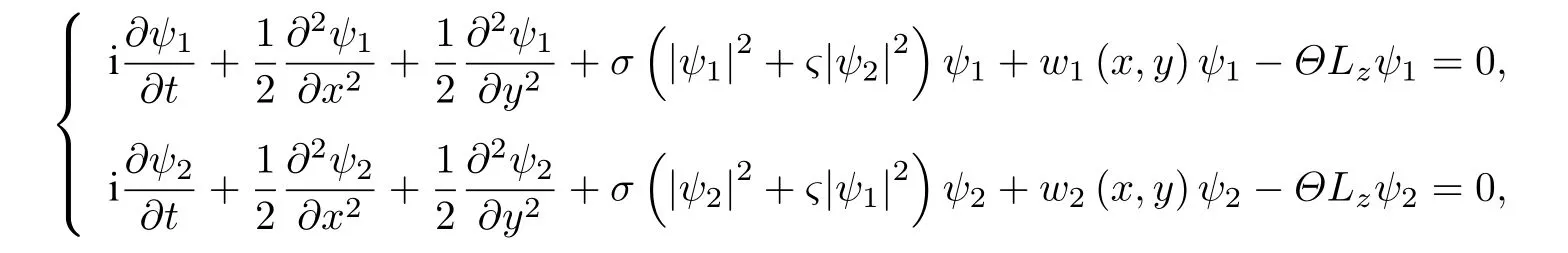
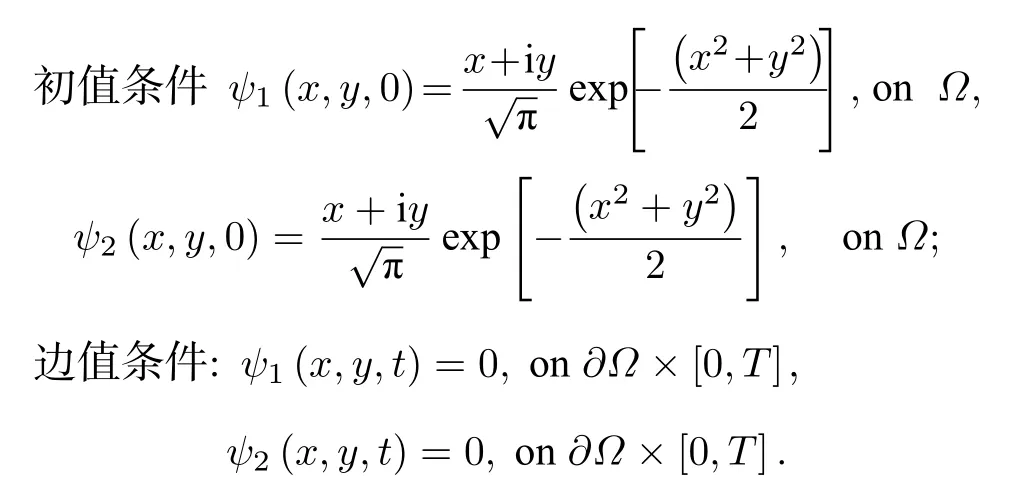
本文模擬中選取w1=w2=1.5x2+0.5y2,Θ=0.7,σ=-100,?=0.8.

圖5給出了兩種數值方法得到的不同時刻沿x軸變化的波函數曲線.由圖5中兩個不同時刻波函數變化曲線可知,BEC動力學特性在角動量旋轉下的變化是復雜的; SS-FPM方法得到的數值結果與SS-FDM法[7]得結果吻合,表明提出的粒子方法模擬預測GP方程描述BEC動力學性質是可靠的.圖6給出了三個物理量 R e(ψ),Im(ψ),|ψ| 三維數值結果,可以明顯觀察到角動量旋轉項影響下隨時間演化的量子化渦旋變化情況.值得注意的是圖5和圖6僅展示了第一分量的數值結果,這是因為根據選取模擬參數兩個分量變化是一致的.

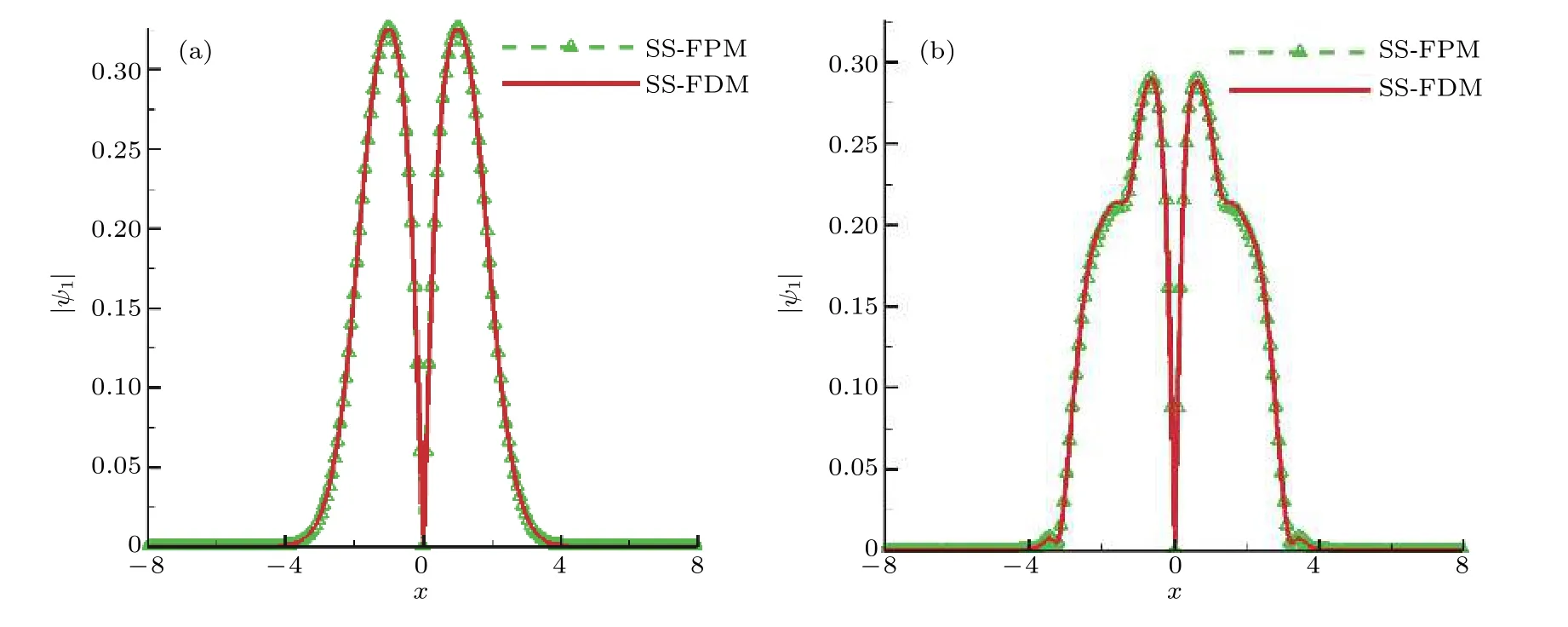
圖5 兩個不同時刻 | ψ| 沿x軸 (y=0)變化曲線 (a)t=0.05; (b)t=0.25Fig.5.The change curve of | ψ| along x-axis (y=0)at two different times: (a)t=0.05; (b)t=0.25.

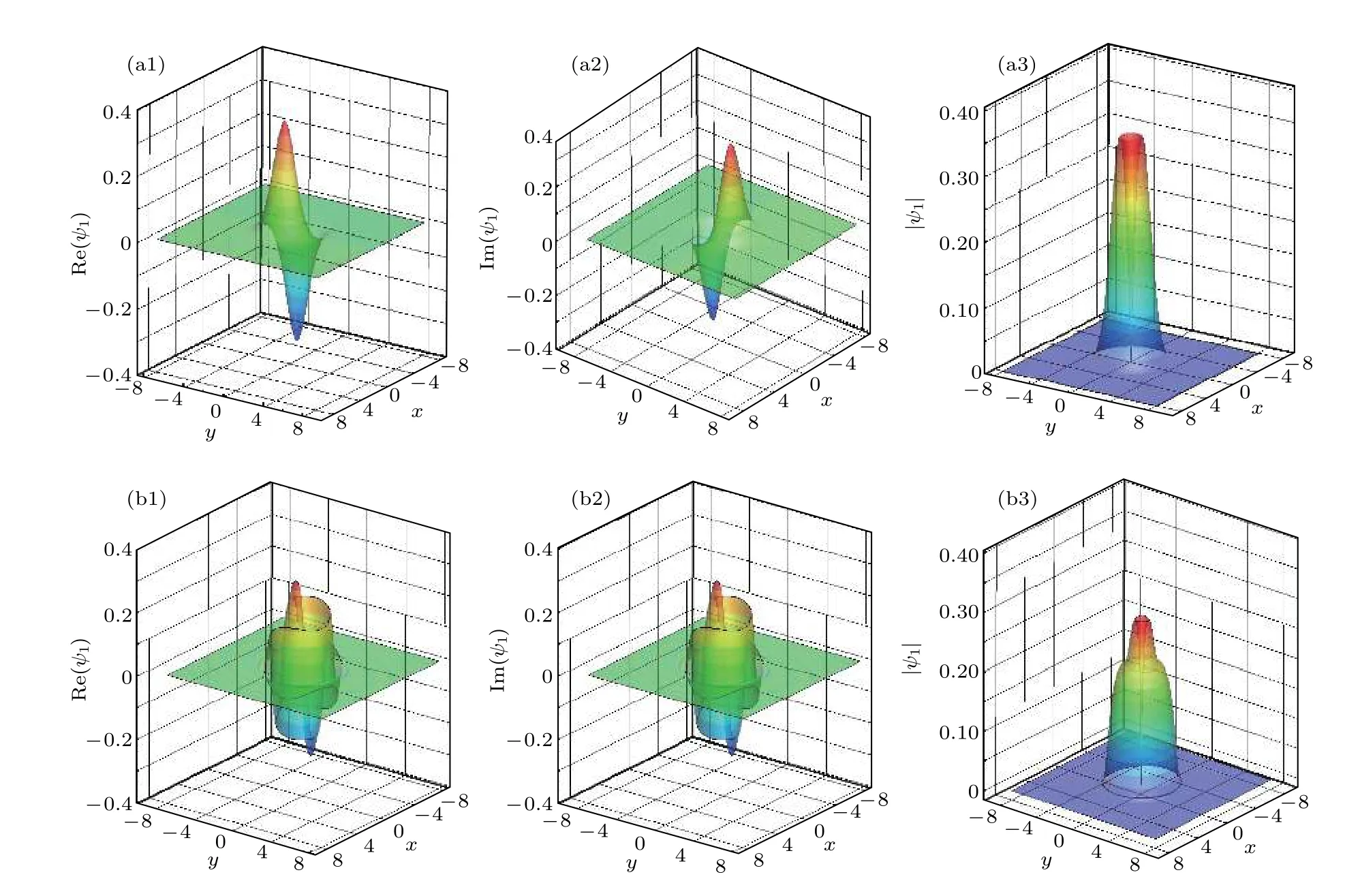
圖6 兩個不同時刻 R e(ψ),Im(ψ),|ψ| 的三維數值結果 (a1),(a2),(a3)t=0; (b1),(b2),(b3)t=0.25Fig.6.Three-dimensional numerical results of R e(ψ),Im(ψ),|ψ| at two different times: (a1),(a2),(a3)t=0; (b1),(b2),(b3)t=0.25.

5 結 論

為提高直接推廣有限點集法模擬二維非線性薛定諤方程或Gross-Pitaevskii方程的數值精度,本文給出了基于分裂格式的有限點集法(SS-FPM),該方法兼顧時間分裂格式和傳統FPM方法的優點.數值算例中,考慮了粒子分布均勻和非均勻情況下帶有不同邊界條件的二維非線性薛定諤方程,并與解析解進行對比,對SS-FPM方法的精度和收斂性進行了分析,驗證了數值預測的準確性; 隨后運用SS-FPM法對無解析解NLS/GP方程進行了數值預測,與其他數值結果進行了比較.數值結果表明:

1)SS-FPM方法模擬二維非線性薛定諤方程具有二階收斂速度,較已有分裂有限差分法具有較好的靈活應用性,且在粒子分布非均勻情況下仍具有較高數值精度;

2)SS-FPM法能夠成功地預測帶周期邊界條件下孤立波傳播過程的奇異現象,且與其他數值結果相吻合;

3)SS-FPM法準確地預測了帶外旋轉BEC二分量的孤立波值量子化渦旋隨時間的演變過程.

目前未見文獻將時間分裂格式與FPM耦合對非線性薛定諤方程進行模擬研究,本文針對不同邊界條件下二維非線性薛定諤方程給出的SSFPM法較網格類方法具有更好的靈活推廣應用性,為復雜區域上含孤立波非線性問題的數值預測提供了一種準確有效的粒子方法.