一類擾動Kadomtsev-Petviashvili方程的雅可比橢圓函數解的收斂性探討*

焦小玉 賈曼 安紅利

1)(南京財經大學應用數學學院,南京 210023)

2)(寧波大學物理與技術學院,寧波 315211)

3)(南京農業大學理學院,南京 210095)

為構造一類擾動Kadomtsev-Petviashvili(KP)方程的級數解,利用同倫近似對稱法求出三種情形下具有通式形式的相似解以及相應的相似方程.而且,對于第三種情形下的前幾個相似方程,雅可比橢圓函數解亦遵循共同的表達式,這可以產生形式緊湊的級數解,從而為收斂性的探討提供便利:首先,對于擾動KP方程的微擾項,給定u關于變量y的導數階數n,若n≤1(n≥3),則減小(增大)|a/b|致使收斂性改善;其次,減小ε,|θ-1|以及|c|均有助于改進收斂性.在更一般情形下,僅當微擾項的導數階數為偶數時,擾動KP方程才存在雅可比橢圓函數解.

1 引 言

對于源于現實問題中各種現象的非線性方程,人們通常研究其數值解.除去數值解之外,近似解析解也有助于非線性方程的研究.非線性方程附加了微擾項則變成擾動非線性方程,這類方程的近似解析解可以利用擾動理論[1,2]結合精確求解方法進行構造.

作為非線性方程的一類精確解析解,群不變解可以通過李群或者李對稱理論[3,4]中的經典或非經典李群法[5]、李對稱方法與直接法[6]進行求解.這些方法通過減少自變量的個數實現偏微分方程的化簡.作為直接法的一種修正,改進的直接法[7,8]貌似與李群理論無關,但是卻可以重構李對稱群甚至離散變換群.

經典李群法用于延拓方程組而不是原偏微分方程可以得到更多的約化,非經典李群法實質為經典李群法應用于原偏微分方程與不變曲面條件組合成的延拓方程組.延拓方程組也可以通過引入輔助變量并且將非局域對稱局域化[9]而產生,這套方案引領了諸如孤立子、cnoidal周期波與Painlevé波等不同類型非線性波之間相互作用的研究[10,11].

擾動理論和李群理論兩種方式結合為近似對稱法: Baikov等[12]提出的近似對稱法實際上是對稱群的近似,因為對稱群生成元推廣至擾動形式;而Fushchich等[13]提出的近似對稱法則是基于擾動方程近似子方程的精確對稱.文獻[14,15]對兩種方法進行了比較,說明第二種方法優于第一種方法.文獻[16,17]進一步推廣了第二種近似對稱法,得到了通式形式的約化方程.第二種近似對稱法甚至可以求出擾動非線性方程的級數解[18].近似直接法[16]改為利用直接法求解這些子方程,則可以得到與近似對稱法相同的約化結果.

擾動理論也可以結合同倫理論以產生同倫分析法[19-21],該方法通過將非線性方程分解為無窮多線性子方程實現非線性方程的化簡與求解.此方法適用于非擾動方程,因而較擾動理論優越,甚至能夠求出擾動方法、人工參數法[22]、δ擾動展開法[23]以及Adomian分解法[24]求解的級數解.

若近似對稱法引入同倫,則同倫分析法的諸多優點能夠得以保留,產生的同倫近似對稱法[25]與同倫分析法的主要區別在于,同倫近似對稱法將非線性方程分解為無窮多非線性子方程.類似地,同倫結合近似直接法可以得到同倫近似直接法[26].

本文的主要目的是探討擾動非線性方程的雅可比橢圓函數級數解的存在性以及收斂性.在第2節,對于具有相似微擾項的一類擾動Kadomtsev-Petviashvili(KP)方程,根據同倫近似對稱法,無窮多約化方程以及約化解的通式形式得以構造.前幾個約化方程的雅可比橢圓函數解亦具有通式形式.第3節主要涉及級數解的收斂性的討論.第4節是結論部分,針對更加廣泛的微擾項,討論了擾動KP方程雅可比橢圓函數級數解的存在性.

2 擾動KP方程的同倫近似對稱

擾動KP方程形如

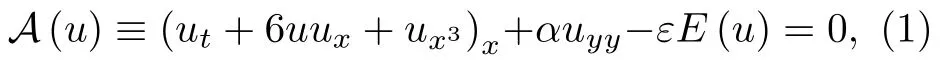
是通過如下KP方程[27]添加微擾項εE(u)而產生的:

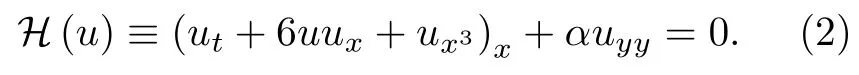
通常,微擾項的補充可以使模型方程對實際問題的刻畫更為貼切.為方便起見,本文采用諸如ux3=uxxx的記號.

擾動KP方程的同倫模型

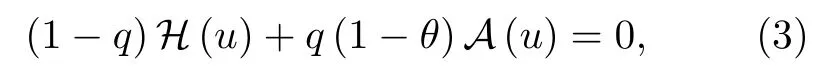
在同倫參數q由0變到1時,逐漸由KP方程轉變為擾動KP方程,這體現了由簡單到復雜的漸變過程.其中,θ/=1是輔助參數.暫取定一類特殊微擾項εE(u)=εux6-nyn,(n=0,1,···,6),即因變量關于空間變量{x,y}的所有六階導數.關于同倫參數q的級數展開

可以將該同倫模型分解為一系列近似子方程

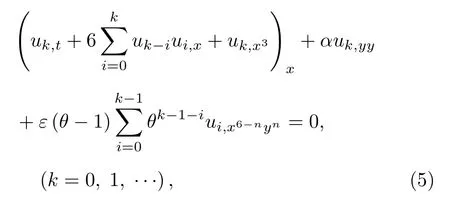
其中u-1=0.本文所有負指標量均取0.這些近似子方程的線性化方程為

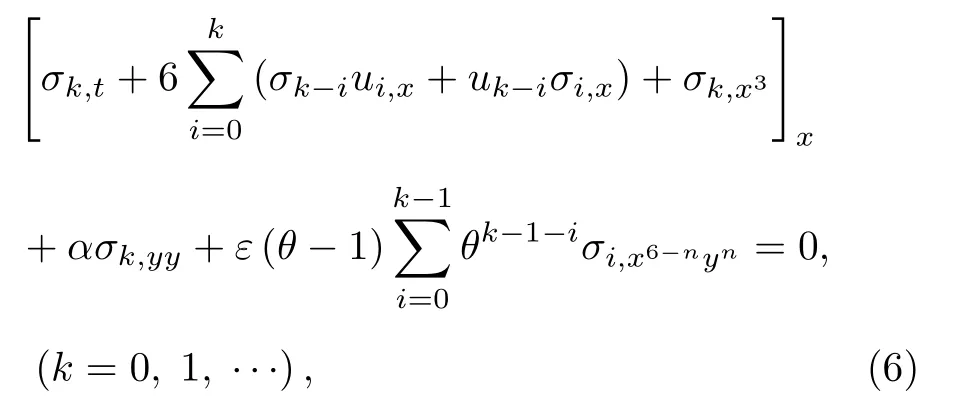
其中函數形式的點對稱為

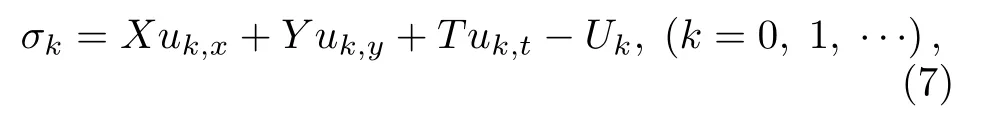
其中{X,Y,T,Uk(k=0,1,···)}的變量為{x,y,t,uk(k=0,1,···)}.

(5)式—(7)式聯立用于決定{X,Y,T,Uk}(k=0,1,···).取定n,將(7)式代入(6)式,利用(5)式消去uk,xt,并且將uk的所有導數系數取0,得到關于{X,Y,T,Uk(k=0,1,···)}的無數方程組成的決定方程組.為簡化求解,僅考慮(5)式的前幾個方程.例如限定(5)式中的k的范圍k∈{0,1,2}.易知{X,Y,T,U0,U1,U2}的變量減少為{x,y,t,u0,u1,u2},嘗試不同的n的取值,反復求解決定方程組,可以推斷決定方程組的解形如

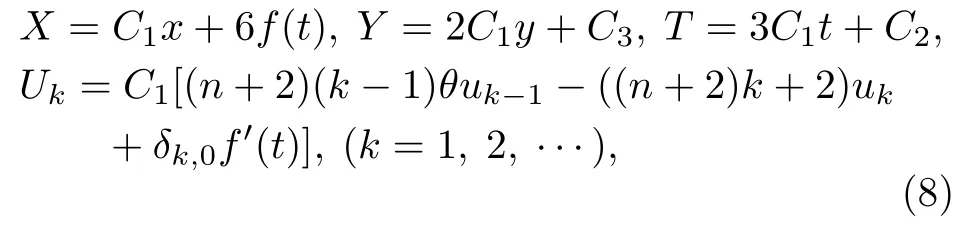
其中,C1，C2都是任意常數;f(t)是關于t的任意函數.滿足δ0,0=1以及δk,0=0,(k/=0)的記號δi,j亦適用于下文.令(7)式中的所有σk取0,求解相應的特征方程,則可以確定(5)式的相似解.

情形1:當C1/=0時,不失一般性,做變換使得如下的相似解不會出現C1

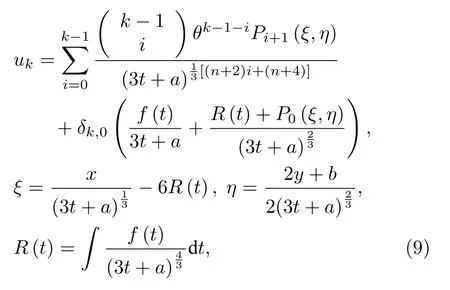
此時,(5)式約化為統一形式

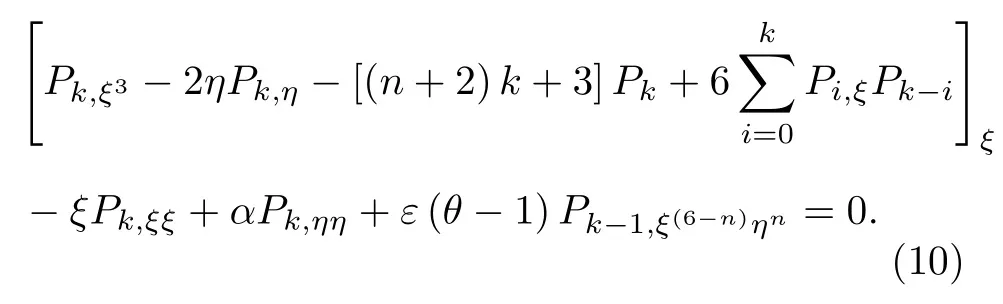
情形2:當C1=0,C2/=0時,不失一般性,做變換求解特征方程,可以得出相似解

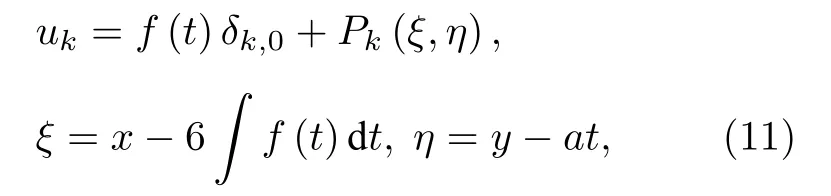
此時,(5)式約化為統一形式

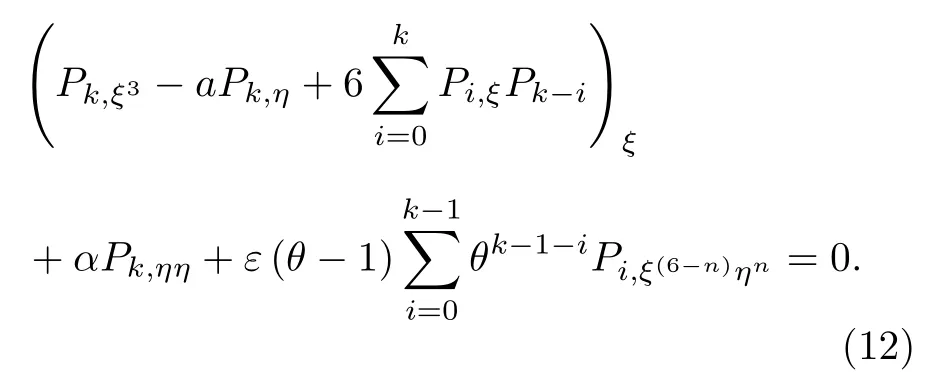
情形3:當C1=0,C2=0,C3/=0時,將C3改寫為a,可得相似解

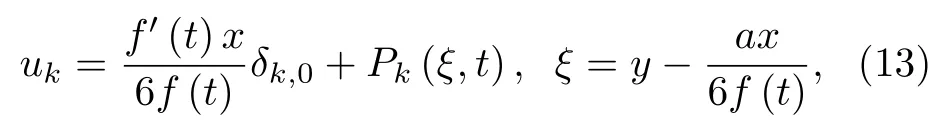
此時,(5)式約化為統一形式

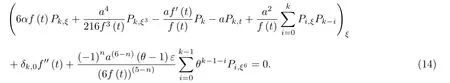
若指標k給定,且{P0,P1,···,Pk-1}已知,以上三種情況的相似方程顯然是關于Pk的四階偏微分方程.

考慮(14)式中約化方程的諸如雅可比橢圓函數形式的特解,做出假設

其中{fk,i,g}是關于所含變量的待定函數.所有fk,i都不是{sni(g(ξ,t),m),i=0,1,2,···}的線性組合.由于(14)式中的系數包含f(t)及其導數,所以這些系數的化簡可以通過假設f(t)為一個常數b實現.此時,這些系數退化為常數.

類似文獻[18]中關于各階約化方程的求解過程,(15)式中Pk的確定也是通過分步求解過程實現的.在第k步中,將已知解{P0,P1,···,Pk-1}以及未知解Pk代入(14)式中的k階方程,再取所有含有{sn(g(ξ,t),m),cn(g(ξ,t),m),dn(g(ξ,t),m)}的各項系數為0,則可以得到(15)式中各項系數fk,i(ξ,t)的方程組.通過求解這些方程組,再回代入(15)式,即可得到約化方程(14)中的前幾個方程的雅可比橢圓函數解(見附錄).

3 擾動KP方程的級數解

在q=1條件下,將(13)式以及附錄中的雅可比橢圓函數解代入(4)式,提取關于sn(cξ+h,m)的不同冪次的系數,可以將級數解重新表示為如下緊湊形式

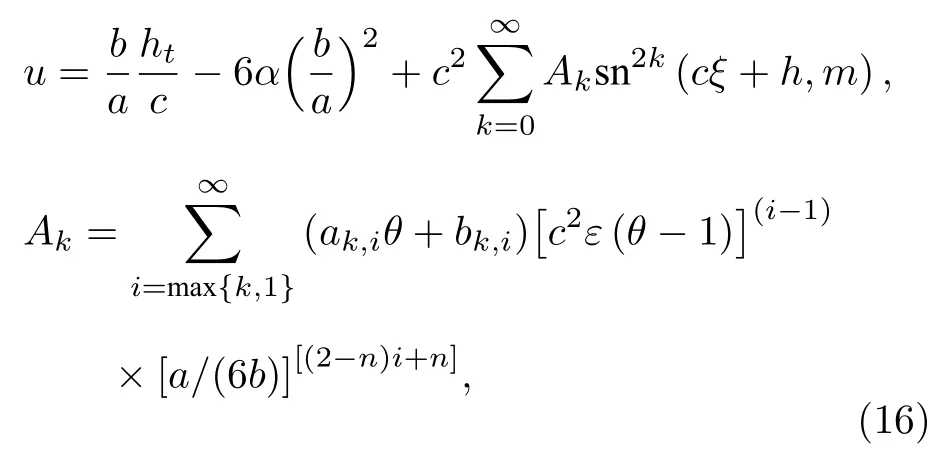
其中ak,i與bk,i只包含常數m.容易驗證,若θ=0,該級數解一定是近似對稱法所得級數解.

已知每個雅可比橢圓函數取值于區間[-1,1],所以,為了確保(16)式的收斂性,須滿足顯而易見,當k增加時,減小?,|θ-1|或者|c|有助于減小|Ak|.任意常數a和b對于收斂性的影響需另當別論.尤其需要注意Ak之中[a/(6b)][(2-n)i+n]的冪次[(2-n)i+n].當n≥3時,對于i≥k有(2-n)i＜0,僅當|a/(6b)|＞1時,成立,此時增大|a/b|可改善收斂性;當n=2時,(2-n)i+n=2.任意常數a和b與收斂性之間沒有明顯關系;當n≤1時,(2-n)i＞0.僅當|a/6b|＜1時,=0成立.此時,減小|a/b|改善收斂性.

當t=0且y=0時,取α=1,h(t)=t,m=0.5,c=1以及ε=0.1,在圖1—圖4中對截斷級數解關于變量x做圖,這些圖可以說明輔助參數θ與比值|a/b|如何影響級數解的收斂性.實線、虛線、點線、點劃線分別表示k取值{0,1,2,3}情形下的級數解在這些截線圖中,相鄰曲線之間相對距離的變化趨勢可用于研究級數解的收斂性.當k增加時,若相鄰曲線之間的相對距離顯著減少,則收斂性得以保證,相應區域可視為收斂域.從這些截線圖容易看出,相鄰曲線之間最大相對距離的區域恰好是波峰與波谷區域.發散區域可以從波峰與波谷區域中尋找.

圖1—圖4中的每個子圖(a),(b),(c),(d)分別對應參數 θ 取值0.90,0.99,1.01,1.10.圖1和圖2取值 n=1 ,而圖3和圖4取值 n=3.圖1和圖3取定 a=2b ,而圖2和圖4取定 a=b/2.從每個圖的各個子圖之間的比較易知,θ=0.99以及θ=1.01兩種情形的級數解的收斂性明顯強于θ=0.90以及 θ=1.10 兩種情形.于是,輔助參數愈接近1,級數解的收斂性愈好.

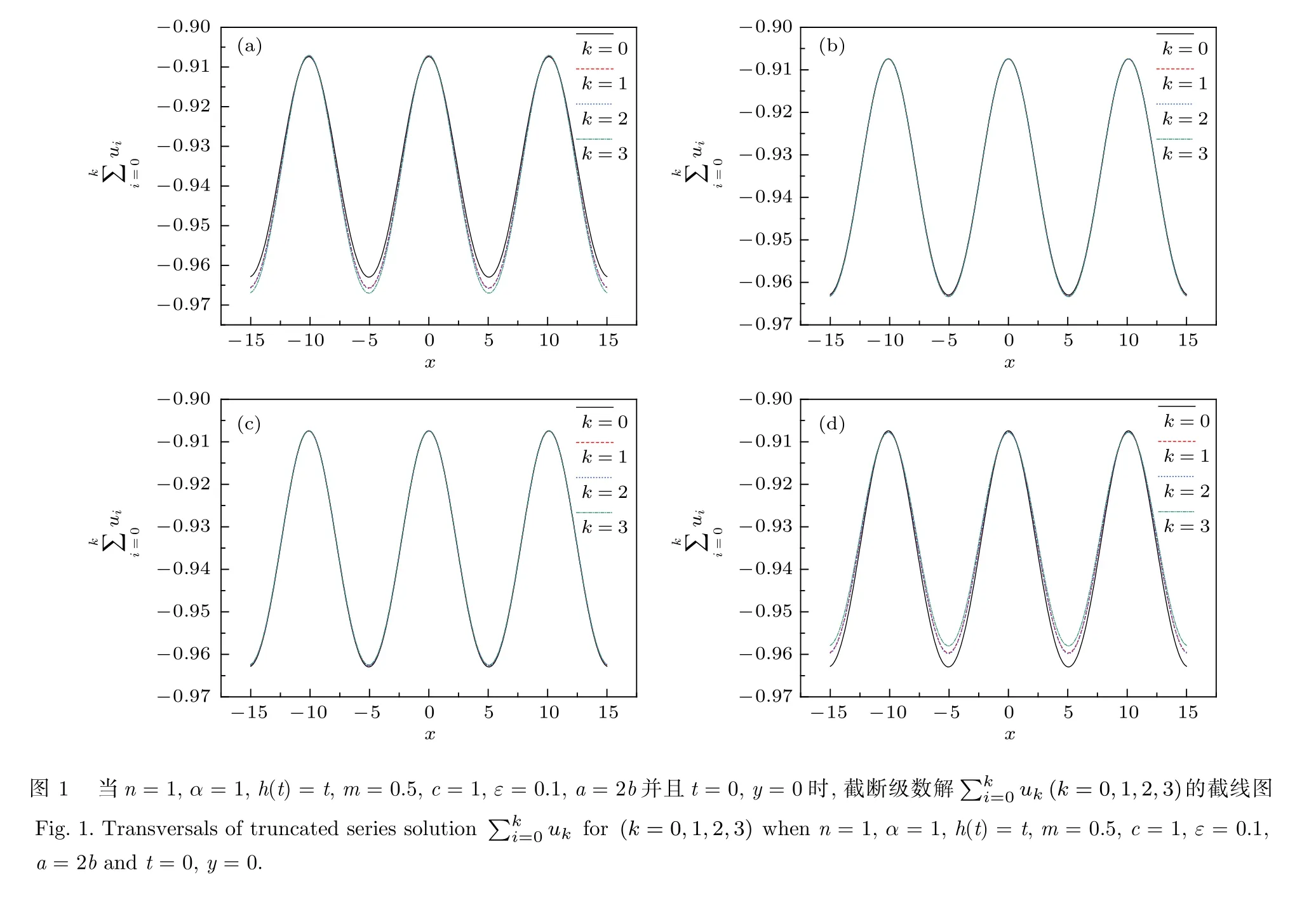
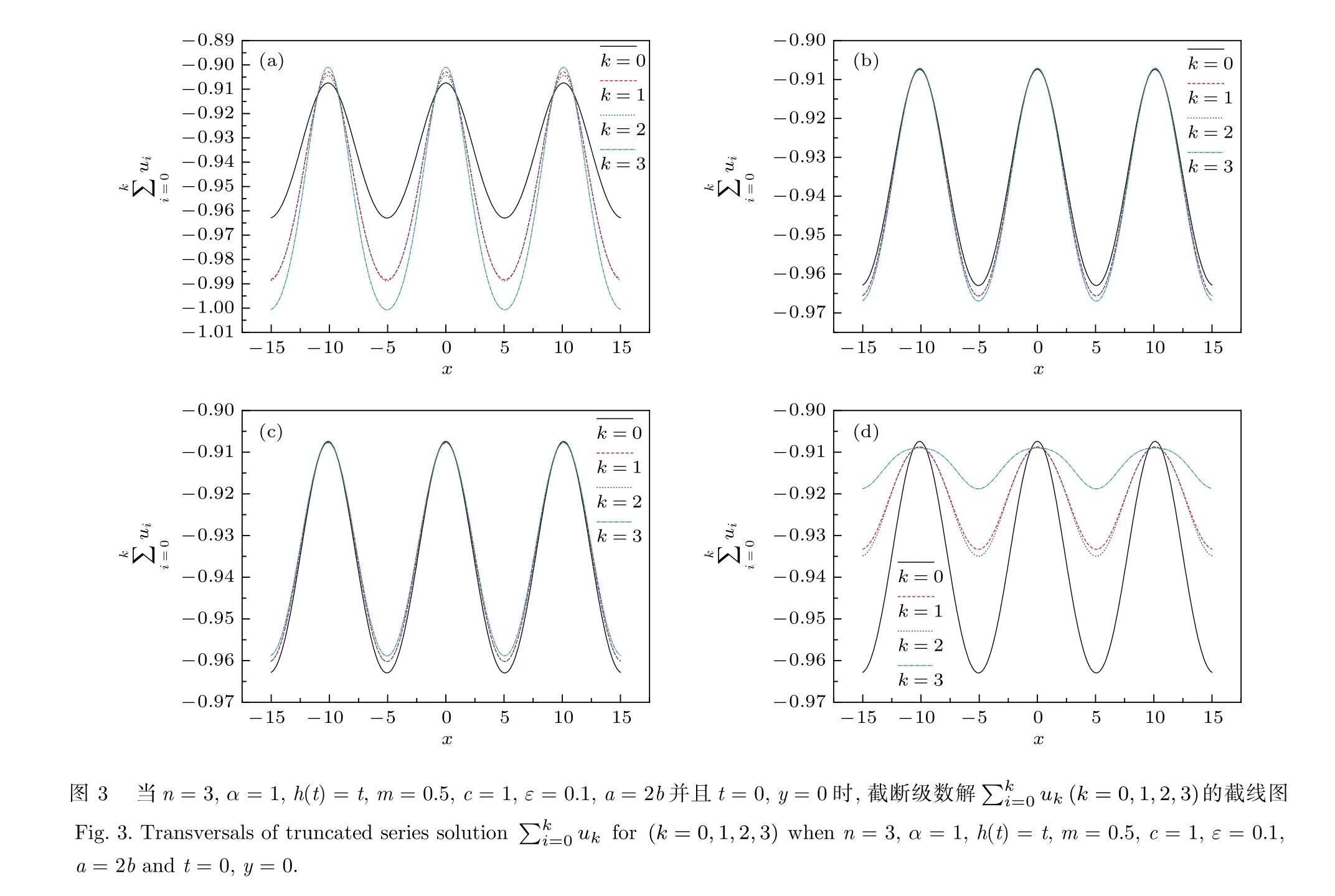
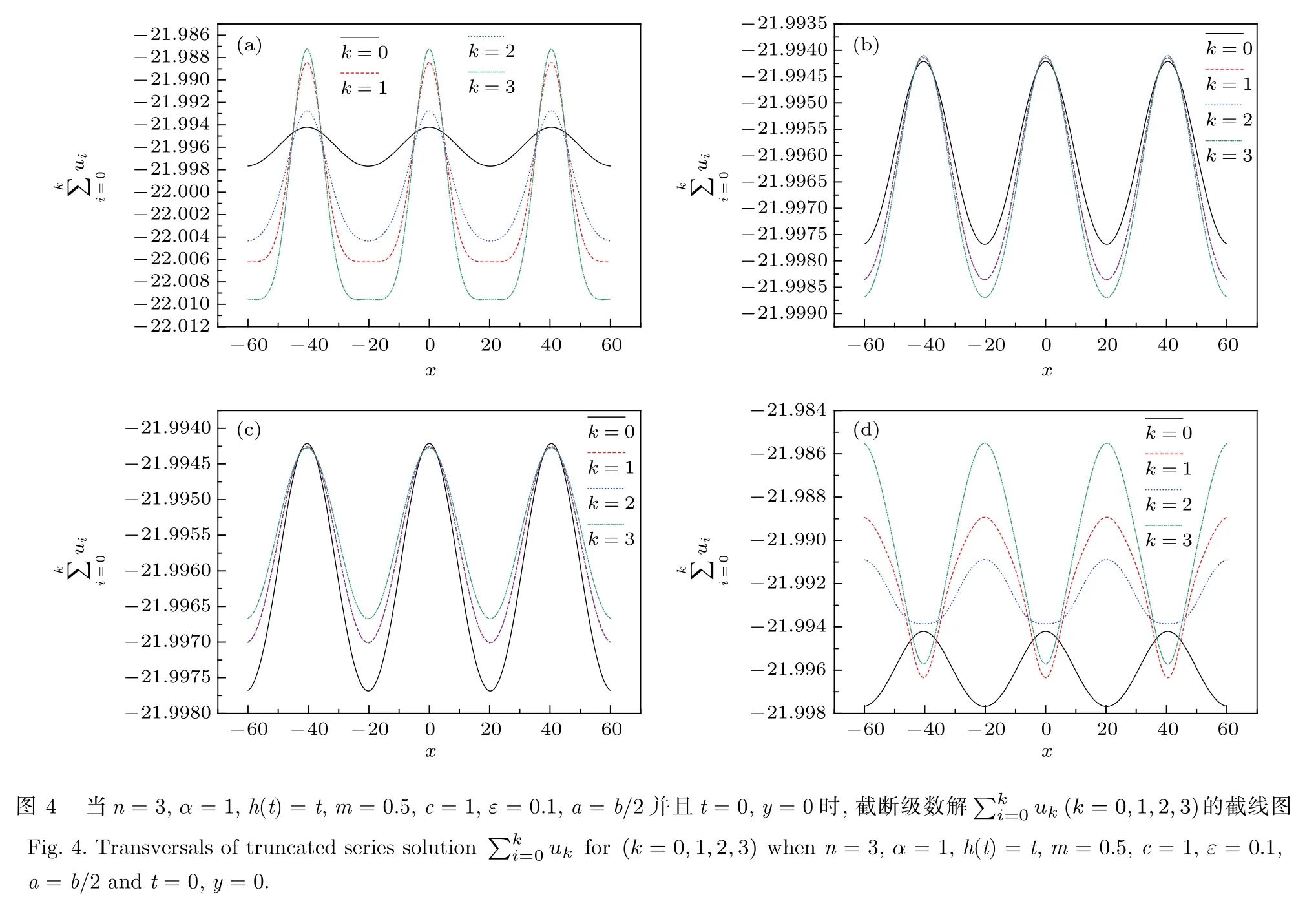
圖1和圖2的唯一區別是常數a和b.比較圖1和圖2的對應圖形可得,a=b/2情形的收斂性強于 a=2b 情形.同樣方式,圖3和圖4的唯一區別也是常數a和b.比較圖3和圖4的對應圖形可得,a=2b 情形的收斂性強于 a=b/2 情形.由于圖1和圖2區別于圖3和圖4之處僅是微擾項中n關于變量y的導數階數n,這也可以說明,若 n ≤1 ,|a/b|取 值越小收斂性越好; 若 n ≥3 ,| a/b| 取值越大收斂性越好.

觀察級數解(16)的表達式,Ak中的表明,滿足且減小可以改善級數解的收斂性.減小 c2,ε,|θ-1|對收斂性的改善效果基本相同,但是三者應區分對待.首先,擾動參數 ε 是小參數,表明實際問題中微擾因素的強弱,具體取值取決于實際問題.其次,在同倫模型(3)式中,θ 越接近1,該模型越接近KP方程而不是擾動KP方程,從而級數解(16)式更好地刻劃KP方程而不是擾動KP方程.最后,減小 |c|有利于改善收斂性,但是,|c| 并不是越小越好,顧及(13)式中的相似變量級數解(16)式可以化為

c的取值對級數解的形態有很大影響: 第一,減小|c|致使級數解的周期變大,波動愈加平緩; 第二,減小 |c|時 ,( b/a)(ht/c)會使級數解急劇增加或減小,級數項的系數 c2會使級數解急劇減小.所以,減小|c|也 應適度.此外,此級數解也表明: 減小 | a/b| 致使x軸方向周期變大.

4 總結與討論

級數解的收斂性依賴于任意常數 { a,b,c} ,擾動參數 ε 以及輔助參數 θ .然而,任意常數{a,b,c}的調整會導致級數解的周期隨之顯著變化.所以,減小擾動參數 ε 是改進收斂性最便捷最有效的手段.不同于任意常數 { a,b,c} ,調整擾動參數不會顯著影響級數解的形態.

附錄 (14)式的雅可比橢圓函數解

其中c為任意常數.