三維地形下基于Hopfield神經網絡的路徑規劃算法

徐 煒 周蘭鳳* 章民融

1(上海應用技術大學計算機科學與信息工程學院 上海 201418)2(上海市計算技術研究所 上海200040)

0 引 言

路徑規劃問題，即按一項或多項優化規則，如最小工作代價、最短行走路程、最短行走時間等，尋找一條從起始狀態到達目標狀態的最優無碰路徑[1]。復雜地形下的路徑規劃是近幾年研究的熱點問題。目前，研究路徑規劃的算法主要有D*算法[2-3]、遺傳算法等，這些算法相對來說單一且僅針對于簡單的地形，在復雜的三維地形中無法適用。神經網絡算法在最近幾年的研究中逐漸迅速并且適用于解決復雜的地形輸入問題[4]，禹建麗等[5]通過對神經網絡在路徑規劃上的應用，解決了最短路徑規劃問題。但這些算法對于起伏地勢較大的三維特殊地形中，依舊缺少對起伏地勢以及障礙物的考慮。

綜上所述，雖然很多人都對路徑規劃問題有所研究，但是，并沒有考慮在復雜地形下的起伏地勢以及障礙物對路徑規劃的影響[6-7]。也就是說，諸多的路徑規劃算法與具體的真實復雜地形存有脫節的現象[8]。本文利用了當下研究較為流行的神經網絡算法，并且考慮到復雜的三維地形環境中地形以及障礙物等問題，將神經網絡與地形函數模型相結合，為自主導航研究奠定了基礎。

1 地形函數模型

1.1 地形預處理

導航車在復雜的三維地形行進過程中，要避開障礙物以及起伏變化較大的地勢，以達到最優的路徑[9-10]。由于地勢的復雜性，無法對其直接進行計算，故地形的預處理是進行建模的第一步。

為此，本文在研究中將高低起伏的地勢轉化為規則的圓柱體，將障礙物轉化為球體，便于導航車在行進過程中避開這些障礙物，尋找到一條最優的路徑。規則幾何體的函數形式如下：

(1)

式中：x0、y0和z0表示地勢起伏以及障礙物的中心點坐標；a、b和c是常數用來控制障礙物的大小；x、y和z用來表示地形的三維坐標值。式(1)可以根據不同的p、q和r值來描述不同的幾何圖形。當p=q=r=1時，表示的是一個球體，即此時的路徑需要避開的是障礙物；當p=q=1且r>1時，表示的是一個圓柱體，即此時的路徑需要避開的是高低起伏的地勢。

1.2 地形函數

地形函數模型旨在導航車行進的過程中，為避開高低起伏的地勢以及障礙物而建立的一種易于處理的模型。不同的地勢一定具有不同的函數模型。本文主要運用流函數的基本思想，即將從障礙物周圍的流動現象中學習，地形被視為邊界條件，通過使用流體力學計算規劃區域中的流場分布來建立。流動控制方程如下：

▽2Φ=0

(2)

式中：▽是微分符號，此方程式為拉普拉斯方程式，Φ為規則幾何體的函數形式，即式(1)。

流動控制方程的邊界條件之一是在障礙物表面即：

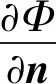
(3)

式中：n表示障礙物表面向外的單位法向量。

邊界條件之二是在無限遠處：

▽Φ=μ∞

(4)

式中：μ∞表示導航車在行進過程中的速度。將式(1)的規則幾何體的函數形式分別代入式(2)、式(3)和式(4)求解，將得到一個適用于避開障礙物和起伏地勢的地形函數模型。

2 連續型Hopfield神經網絡

Hopfield神經網絡是一種遞歸型、結合存儲系統和二元系統的神經網絡，由Hopfield等采用模擬電子線路實現，并成功地求解了優化組合問題中一些最具有代表性的問題，也開啟了信息處理中運用人工智能技術的新方法。該網絡中神經元的激活函數為連續函數，因此，也被稱為連續型Hopfield神經網絡[11-12]。在連續型Hopfield神經網絡中，各神經元一般采用并行工作方式，輸入和輸出均為模擬量。

在生物系統中，由于神經元i的細胞膜輸入電容ci、跨膜電阻Ri和確定阻抗Rij=Wij-1,Wij為i與j之間的權重，狀態Ui會滯后于其他神經元的瞬時輸出Vi，所以神經元的輸出將是0、1之間的連續值，而不是離散模型的二值。連續性Hopfield神經網絡中，組成電路的基本器件如圖1所示。

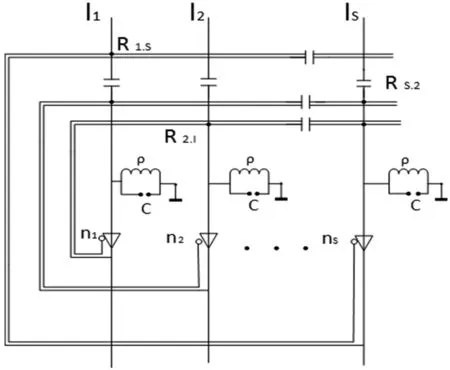
圖1 Hopfield神經網絡的電路基本器件圖

其主要由以下幾部分組成：

(1) 帶有同向和反向輸出端的運算放大器，且具有飽和非線性特性的S型輸入輸出關系，即：

(5)

式中：U0相當于輸入信號的放大倍數，也控制激活函數的斜率，當U0趨近于0時，f就成為二值閾值函數。

(2) 放大器的輸入電容Ci和輸入電阻Ri的乘積為神經元的時間常數，該時間常數表示了神經元的動態特性。

(3) 網絡神經元連接的權值：

(6)

式中：Rij為連接電阻。

(4) 外加偏置電流Ii相當于神經元的閾值θi，整個電路系統的動態方程式為：

(7)

若式(7)有解，那么系統狀態的變化最終會無限接近穩定。在對稱連接和無自反饋的狀態下，可定義系統的能量函數為：

(8)

式中：T代表網絡神經元連接的權值；V和I分別表示某個神經元的電壓和電流；f常取雙曲線正切函數。穩態時，可忽略最后的積分項得到：

(9)

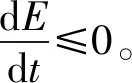
至此，有了Hopfield神經網絡的模型的狀態方程和能量函數，可以來嘗試解決三維地形下的路徑規劃問題。

3 三維地形建模

為有效地建立三維地形的模型，本文在研究中引入高度圖作為輸入數據的方法。高度圖是創建三維地形的標準方法，它是一個二維數組值[13]。數組中的每個值表示該值位置處的地形高度[14]。例如，圖2顯示了高度圖的單元格和每個單元格的值，而圖3顯示了該地圖生成的地形線框視圖。

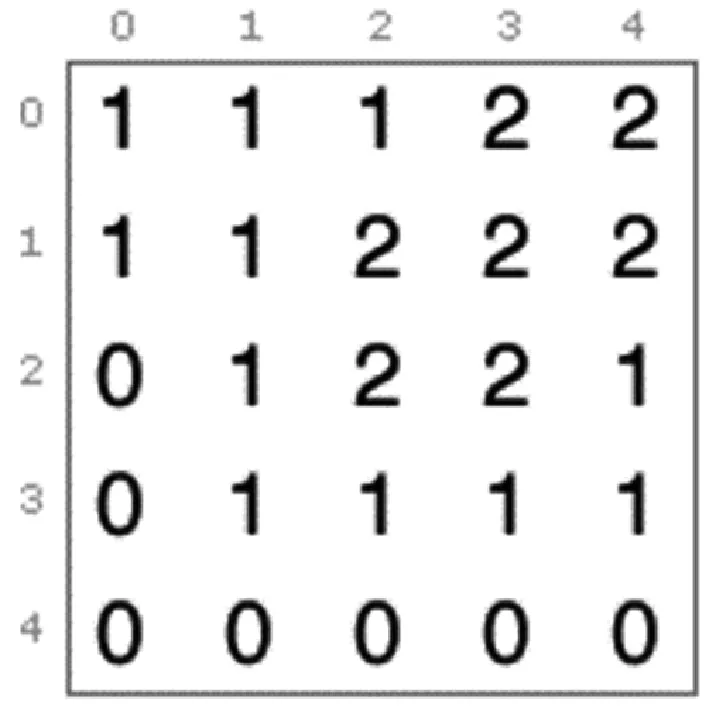
圖2 高度圖的單元格和值

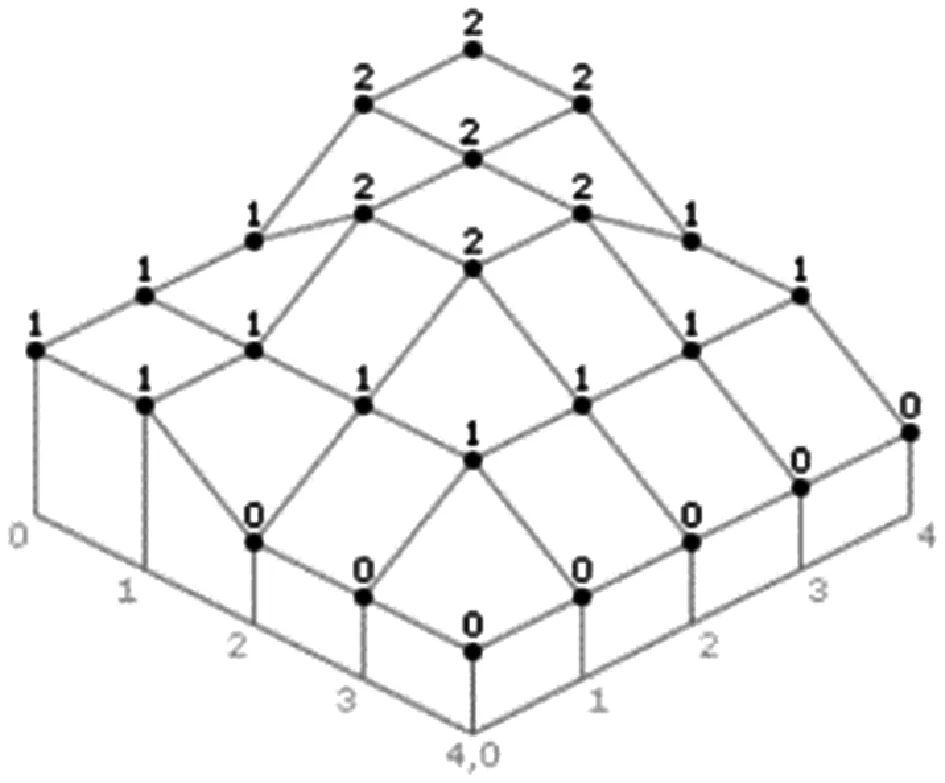
圖3 生成的地形的線框視圖

三維地形的建立需要基于高度圖并且迭代地使用不同的算法。本文選擇山丘算法構建三維地形模型。其基本算法步驟如下：

步驟1將所有高度值初始化為零；

步驟2在地形上或附近選擇隨機點，以及在某個預定的最小值和最大值之間的隨機半徑，選擇這個最小值和最大值將使地形變得粗糙或者光滑；

步驟3在具有給定半徑的點的中心上升起山丘；

(一)離合詞“A了個B”的概念重組之后表示的是動詞的量，表次數；而網絡詞“A了(嘞)個B”則是純形式，概念重組之后仍繼承的是指向決定體的意義，只是因為音節的增多而使得語氣緩和，風格幽默。如“出了個丑”表示的是出丑的量，一次。又如：

步驟4返回步驟2，并根據需要重復迭代多次，選擇的迭代次數將影響地形的外觀；

步驟5規范地形。

至此，三維地形的模型建立完成。將運用此三維地形進行路徑規劃算法的研究。

4 三維地形下路徑規劃算法

連續型Hopfield神經網絡在處理數據時是同步進行的。若將一個路徑規劃問題的目標函數轉換成連續型Hopfield神經網絡的能量函數，把問題的變量對應于網絡中神經元的狀態，那么，連續型Hopfield神經網絡就能夠很好地應用于路徑規劃問題。并且，將地形函數模型考慮進能量函數內，那么，Hopfield神經網絡就能夠更好地處理三維地形的障礙物以及起伏地勢的問題。當網絡的神經元狀態趨于平衡點時，網絡的能量函數也趨于最小值，網絡由初狀態向穩態收斂的過程就是路徑的最優解過程。

本文設計了Hopfield神經網絡的能量函數與目標函數相對應，因此網絡的能量函數包含目標項及約束項兩部分，將網絡的能量函數定義為：

(10)

式中：V表示神經元的輸出；N表示神經元數量；A、B、C和D為權值。

除此之外，為了能夠更好地處理三維地形中的障礙物以及起伏地勢的問題，必須加入地形函數模型信息：

(11)

由式(11)和式(12)兩部分的結合可以得到路徑規劃問題的網絡能量函數：

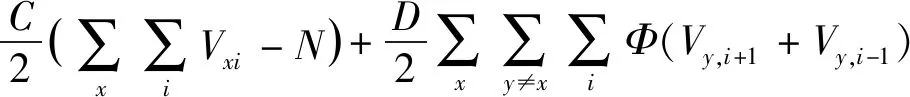
(12)

具體的算法步驟如下：

步驟1創建三維地形圖；

步驟2初始化網絡；

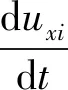
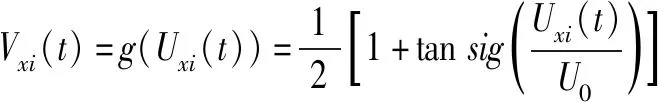
計算Vxi(t)；

步驟5計算網絡能量函數E；

步驟6若迭代次數p>10 000，則結束程序,否則,p=p+1,返回步驟3。

5 實驗結果與分析

實驗在Unity 2018中進行。首先使用山丘算法建立三維地形圖，如圖4所示。其中，規則幾何形狀代表行進路徑中的障礙物，其余部分是起伏地形。未對起伏的地形和障礙物進行處理之前，使用Hopfield神經網絡的路徑如圖5所示，可以看出此路徑不能避開起伏的地形和障礙物。然后，利用地形函數模型對起伏的地形和障礙物進行處理，且并入Hopfield神經網絡算法中進行路徑規劃的路徑如圖6所示，可以看出該路徑有效地避開了起伏的地形和障礙物。

圖6 加入地形函數模型的路徑圖

6 結 語

本文以Hopfield神經網絡為背景，研究三維地形下的一種有效的路徑規劃問題。利用山丘算法建立三維地形模型，在這個三維地形中，首先對起伏的地形以及障礙物進行處理,得到地形模型函數，然后在Hopfield神經網絡算法中集成此地形函數模型。實驗表明，在復雜的三維地形中該算法可以避開起伏的地形和障礙物，尋找到一條有效路徑。本文研究也為無人駕駛的自主導航奠定了基礎。