基于FLAC3D的巖質邊坡爆破動力響應規律研究

唐旭　方正峰　鄒飛

摘要：邊坡的動力穩定一直以來都是巖土工程及地震工程重點研究的問題。利用FLAC3D數值計算方法，對爆破作用下巖質邊坡振動速度、位移、應力等進行模擬，并在與實測爆破振動峰值進行對比驗證的基礎上，分析邊坡的動力響應規律。結果表明：地震波具有極強的方向性，主要朝施加荷載的正向傳播;在邊坡坡面和坡腳處因應力波在邊坡自由面反射容易產生一定區域的振動加強場;應力的響應特征上，無論是拉應力還是壓應力其最大值均出現在坡腳附近，在實際的邊坡爆破開挖過程中，對邊坡的坡面尤其是坡腳處應該加強保護措施。研究成果對巖質邊坡開挖設計及施工具有一定的參考價值。

關鍵詞：動力響應;巖質邊坡;FLAC3D;爆破

中圖法分類號：P642

文獻標志碼：A

DOI：l0.16232/j.cnki.1001-4179.2019.03.035

1研究背景

爆破作為一種最有效、最經濟和最便捷的施工方法已經普遍應用到山地公路路塹巖質高邊坡的形成中。巨大的工程規模伴隨而來的是大量的爆破施工作業，而邊坡的動力穩定一直以來都是巖土工程及地震工程重點研究的問題之一。

隨著科技的發展，越來越多的研究人員借助計算機進行仿真模擬，提出了各類數值分析方法，并開發了相應的數值分析軟件，如基于動力有限元法的Ansys/Ls-dyna模塊[1]，離散元法的UDEC[2]，快速拉格朗日法的FLAC3D等[3-4]。

蔣楠用Ansys/Ls-dyna建立了不同坡度的邊坡爆破振動數值計算模型，獲得了不同坡度邊坡在同一水平位置的各坡面監測點的質點爆破振動速度變化趨勢，且同一爆源距的質點峰值振速隨高程增大表現出高程放大效應;在邊坡坡度相近時，質點振速隨爆源距及高程的同時增加，高程效應不明顯;不同坡度邊坡，在同一水平質點振速隨著邊坡坡度增加以衰減為主，即質點振速在爆源距增加及高程增加的同時作用下，而不再表現為常規的振動速度隨爆源距增加衰減的現象，而是以質點振速隨高程增加而呈現增長的現象[5]。唐海，李海波等應用UDEC程序模擬了爆破振動波在不同地貌中的傳播特征，得出凸形地貌下放大系數并不隨臺階型凸形地貌的增高而單調增加，在孤立凸形地貌下，放大系數還與凸形地貌的高寬比有關[6-7]。言志信、祁生文等利用FLAC3D軟件對不同坡高、坡角的邊坡動力響應特征做了數值計算分析研究，獲知當邊坡坡高較低時，在一定的坡高范圍內邊坡內的質點振動速度隨著高程的增大表現出高程放大效應，且速度放大系數等值線圖呈近等間距分布;當邊坡的坡高高出一定的范圍時，邊坡質點振動速度不再隨高程的增大表現出線性的反放大，而是表現出節律性的變化，在坡肩附近時，才再一次表現出放大的跡象[8-9]何錚等結合西南某水電戰順層巖質高邊坡工程實例，研究了該邊坡地震后工程地質特性，恢復邊坡震前的地形地貌，建立地震前未滑塌邊坡的三維模型，而后利用FLAC3對模型進行動力-時程響應分析，繪制出位移、速度、加速度三量放大系數等值線圖[10]。

巖質高邊坡爆破開挖過程中引起的地震效應已成為影響邊坡穩定性的重要誘發因素之一，越來越多的學者也開始關注巖質高邊坡在爆破荷載作用下的動力響應特征問題。爆破荷載對邊坡的穩定性影響主要是動荷載作用下巖體的響應特征問題[11-12]，因此掌握并深入分析巖質高邊坡對爆破振動效應的響應特征規律，探索爆破開挖施工對邊坡穩定性的影響，對于進一步控制和預測爆破振動效應對巖質邊坡的危害，同時減少爆破作業對周邊環境的影響具有重要的指導和實踐意義[13-15]。

本文利用FLAC3D建立公路巖質邊坡的數值分析模型，分析巖質邊坡爆破振動下振速、位移、應力相應的響應特征，得到并分析巖質邊坡爆破振動下振速、位移、應力相應的響應特征，細化研究傳播路徑中地質條件、地貌特征的影響。

2FLAC3D動力計算原理

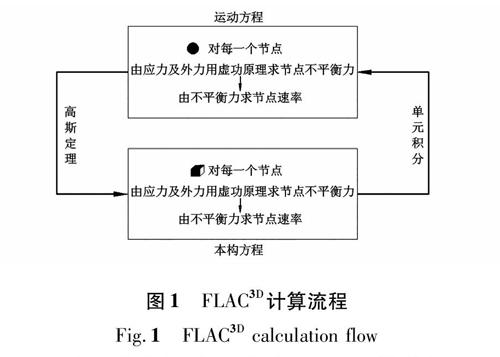
FLAC3D的基本原理是采用線性顯式拉格朗日差分算法和混合離散技術求解運動方程，將指定計算區域劃分成若千個單元，單元之間由節點連接，在對某一節點施加荷載后，此節點的運動方程可以表示為時間不長的有限差分形式，在一微小時間步長內作用于節點的荷載只對相鄰的一些節點產生影響，即根據某一t時刻的應力狀態和△t時間步長應變增量，進而確定t+△t時刻的應力狀態。根據高斯（Gauss）定律，由節點的速率求解單元的應變增量;再利用應力-應變關系，即本構方程計算單元應力，并對其進行積分，得到作用在節點上的應力矢量;最后結合平衡方程，由節點力進一步求解出節點速率及位移。如此反復循環迭代，這一過程將隨時間步長正常擴展到整個計算范圍直至計算收斂，從而準確地模擬巖體及其他材料的塑性破壞和流動。其計算流程如圖1所示。

在速度和位移的動力計算中，FLAC3D以節點為計算對象，分別將質量和力都集中在節點上，再通過運動方程在時域內進行求解，節點運動方程可以表示為

公式

式中，Fli（t）為t時刻l節點在i方向的平衡力分量，可由虛功原理導出;ml為l節點的集中質量。

將式（1）左邊用中心差分來近似，則可以得到節點的速度：

公式

此時，可以進一步得到節點位移：

公式

3數值計算模型的建立

3.1計算模型

圖2為某高速公路K86+152～K86+600段地形地貌示意圖，本文依托該工程對巖質邊坡爆破振動響應特征進行數值研究。

本文采用三維計算模型，X正向為邊坡右側，Y正向為線路大里程方向，Z軸鉛垂向上，模型計算區域為252mx230mx137m。。輸入波動的最短波長控制著網格劃分的尺寸，研究表明，當網格的最大尺寸為△l時，輸入波動的最短波長為λ時，必須滿足△lt<（1/10～1/8）λ。所建立模型及其網格劃分如圖3所示。

3.2本構模型及材料參數

本文模型選取莫爾-庫倫（Mohr-Coulomb）彈塑性模型，該模型用于描述巖土體的力學行為。

該里程段巖性較為均一，僅為灰巖。模型中所需的巖石物理力學參數根據室內實驗確定，詳見表1。

3.3吸收邊界

在FLA3D中可以設置吸收邊界（也稱靜止邊界、黏性邊界）和自由場邊界來減少邊界中波的反射。

本文將X正、負向，Y正、負向4個側面及Z負向地面均設置為黏性吸收邊界，地表均為自由邊界，詳見圖4。

3.4等效荷載輸入

炸藥在爆炸瞬間產生高溫高壓的爆轟氣體，作用于炮孔壁，使其產生破碎區和塑性變形區，并且瞬間衰減為應力波沿巖體繼續傳播，整個過程僅僅持續數毫秒。其間影響因素甚多且極其復雜，目前量測技術有限，無法量化并準確地獲知爆炸過程中的每一個具體細節，只能通過相關經驗將爆破過程中荷載作用及變化情況等效處理，通常是將數值模擬中假定荷載以應力時程的形式輸入。本文擬采用三角脈沖荷載，這種荷載的建立需要確定兩個基本因素[16-19]。

3.4.1爆破振動峰值荷載

峰值荷載的確定即確定炸藥爆炸過程中產生的爆轟氣體作用在炮孔壁上的峰值壓應力。根據爆轟波的C-J理論，炸藥作用在炮孔壁上的平均炮轟壓力為

公式

式中，Pj為瞬時炸藥爆轟平均初始壓力;ρe為炸藥密度;D;為炸藥爆轟速度;γ為炸藥的等熵系數，y的取值與裝藥密度有關。研究表明[20]，當ρe<1.2g/cm3時，γ取2.1，當ρe≥1.2g/cm3時，y取3。

在耦合裝藥條件下，炸藥作用在炮孔壁上的初始峰值壓力P0為

P0=Pj

在不耦合裝條件下，炸藥作用在炮孔壁上的初始峰值壓力為

公式

式中，k為裝藥徑向不耦合系數，

公式

分別為炮孔直徑和藥卷直徑。

研究表明，爆轟氣體作用于炮孔壁時，其壓力將明顯增大，故得到不耦合系數較小的柱狀藥包爆炸對炮孔壁的沖擊初始峰值壓力為

公式

式中，n為爆炸產物膨脹作用炮孔壁時的壓力增大系數，n=8～10，本文取10;l為軸向不耦合系數，

公式

;le、lb分別為裝藥長度和炮孔長度。

表2為爆破荷載峰值壓力計算相關計算參數。

3.4.2爆破荷載作用時間

炸藥爆炸作用時間非常短，通常認為炸藥爆破時沖擊波作用的持續時間約1.0x10-6～0.1s，爆轟氣體壓力作用時間約為1.0x10-3～0.1s。本次數值計算中爆破荷載作用時間假設為7ms，其中爆破荷載壓力上升時間為1ms，'下降時間為6ms，且荷載按現場實際爆破設計情況單排爆破作用于K86+320～K86+350段第一級邊坡坡面上，圖5為爆破荷載施加示意圖。

3.5力學阻尼的選取

巖體中的內摩擦以及可能存在的接觸表面滑動是產生阻尼的主要原因。在動力計算中，動力反應的阻尼需要在數值模型計算分析時模擬重現自然系統中動荷載作用下的阻尼大小。

FLAC3D的動力計算中提供了3種阻尼形式，分別為滯后阻尼、局部阻尼及瑞利阻尼。實踐證明，瑞利阻尼因其理論與常規動力分析方法類似，雖然采用瑞利阻尼時的計算時間步長較小，但是計算得到的加速度響應規律相較于前二者更加符合實際情況，故也是動力計算中通常使用的阻尼形式。

綜合考慮模型計算時間及其模擬的準確性，經過反復調試，本文選取最小臨界阻尼比為0.02，最小中心頻率為10Hz。

4數值計算結果驗證

為了驗證數值計算結果，依托某在建高速公路爆破施工工程現場監測數據，實際爆破參數設計如下。

（1）鉆孔直徑d=90mm。

（2）臺階高度H=10m。

（3）最小抵抗線W光=K光d=20x120mm=2400mm，式中W光為光面爆破最小抵抗線，K光為光面爆破計算系數，一般取K=15～25，巖石越硬K取值越小。該工程取K=20。

（4）炮孔超深h=0.5～1.5m，孔深大和巖石堅硬完整者取大值，反之取小值。此工程取h=1.0m。

（5）孔距光=mW=（0.5～0.8）x2.4=（1.2～1.92）m，式中m為裝藥密集系數。該工程取光=1.2。

（6）炮孔長度L=（H+h）/sin。當坡度為1：0.75時，L=13.8m;當坡度為1：0.5時，L=12.3m。

在模型上布設相應監測點來跟蹤監測其速度時程，位于K86+335斷面的5個監測點位置，詳見圖6。因選取的數值計算荷載施加相關計算參數與現場監測時的實際爆破設計裝藥參數相近，且該工況實際測點布置與數值模型中測線位于同一斷面，將二者峰值振動速度進行對比，得到數值計算各監測點時程曲線如圖7所示，表3為數值計算各監測點與現場監測點峰值振動速度對比結果，并將其繪成折線圖如圖8所示。

由表3及圖8可知，數值模擬結果與現場監測各測點峰值振動速度在爆源近1～3號測點區其相對誤差均在10%以下，到了爆源遠區誤差相對較大，且數值模擬峰值振速普遍大于現場監測數據，可能原因是簡化模型為均勻連續介質，忽略了實際巖體內部節理裂隙等不連續結構面，故而使爆破振動地震波的衰減速度相較與實際工程略有減小。總體而言，數值計算結果的精度尤其是在爆源近區的都在可接受范圍內，說明借助FLAC3D研究該邊坡爆破振動動力響應特征是可行的。

5動態響應分析

5.1速度響應分析

圖9為爆炸后5，10ms時模型X向速度分布云圖。由圖可知爆破地震波的作用影響范圍，因爆破振動地震波具有方向性，特別是對于這種深孔臺階開挖，隨著時間的推進，雖說爆破荷載施加的反方向巖體也有一定的響應，但爆破振動地震波主要朝著施加荷載的右邊坡傳播。總的來說在這種邊坡爆破中，地震波的傳播可以概化成如圖10所示的橢圓等振線。故可以得到的結論是，右邊坡的爆破開挖對既有左邊坡影響可以忽略不計。

圖11為爆炸后5，10ms時K86+335斷面X向速度分布云圖。可清晰地觀察到，隨著爆破地震波的傳播，在坡腳右側某一半徑內質點振動速度在某一區域得到加強，其原因是應力波在邊坡自由面反射而產生了一定區域的振動加強場;又根據圖11（b）所顯示的各臺階周邊速度大小分布情況可知，該時刻速度值在第2級臺階坡腳處形成一個極大中心，順坡而上其速度值是先減小又增大，并在第4級臺階坡腳處再次形成一個極大中心，隨后減小。

5.2位移響應分析

為進一步研究邊坡在爆破振動荷載作用下相關參數的響應特征分布情況，引入無量綱位移放大系數，其定義為邊坡爆破振動位移響應大小與第1級臺階邊緣位移大小的比值。

根據數值計算結果，繪制出邊坡地表及K86+335斷面在10ms時Z向位移放大系數等值線圖如圖12所示。由圖12（a）可知，位移響應特征與前述地震波橢圓等振線分布情況基本一致。圖12（b）中的位移放大系數等值線分布情況再次反映了右邊坡爆破開挖未對左邊坡造成的影響。為進一步分析邊坡坡體內的位移響應特征規律，將圖12（b）右邊坡局部放大顯示如圖13所示。

由圖13可知，爆破荷載施加的1級邊坡其位移在一定深度范圍內隨深度的增加而出現極大中心，超過某一深度后位移放大系數減小;再觀察位移放大系數等值線隨高程增加所表現出來的特征時發現，其分布規律為位移放大系數在1級邊坡表面先減小，順坡面而上在進入2級臺階時位移放大系數逐漸增大，隨后在2級邊坡中部位置順坡面而上位移放大系數開始減小。此時位移放大系數所表現出的分布規律與速度響應大小的分布規律近乎一致。

5.3應力響應分析

圖14為K86+335斷面炸藥爆炸后不同時刻最大主應力分布云圖。

由圖可知，各個時刻除爆源附近一定區域內應力在進一步不斷地調整，邊坡其他區域等值線變化不大，其原因是所施加的荷載相較于自重荷載比較小，尚不足以使整個邊坡的應力重分布。因爆破地震波主要以壓縮波在坡體內傳播，爆破荷載作用下邊坡受影響區域多出現正常的壓應力，但在局部如邊坡坡腳附近、個別坡面及臺階邊緣，會出現一定區域的拉應力，而出現拉應力的區域基本上都是接近坡面，即自由面，其可能原因是爆破振動應力波在自由面發生發射，進而生成一定的拉伸波造成相應區域出現拉應力。

由圖14可知，爆后隨著應力的逐步調整，無論是拉應力還是壓應力，最大值均出現在坡腳，即靠近爆源附近，且相應的應力值均小于巖石相應的臨界強度值，在實際的邊坡開挖爆破中，也是坡腳處最容易率先發生局部的失穩破壞。又由6～10ms的應力分布云圖可知，壓應力主要集中區域在該時段內逐漸向深處移動，而因應力波逐漸傳播至坡面，同時在坡面發生反射，生成一定的拉伸波，該時段坡面逐漸開始產生拉應力，且逐漸地在坡面附近產生拉應力集中區域;10ms過后，坡面周邊拉應力集中區域逐漸消散，僅在邊坡坡腳及1，2級臺階突出物保持著較小拉應力集中區。同時，在10～1000ms，受爆破動荷載影響，較大的坡腳及1，2級臺階附近的應力狀態幾乎不發生變化，應力調整基本趨于穩定，其余部分逐漸向初始狀態下的應力分布進行調整。

6結論

（1）邊坡開挖爆破中，地震波的傳播可以概化為橢圓等振線，地震波主要朝施加荷載的正向傳播，對既有左邊坡的影響較小。

（2）在巖質均一的邊坡中，無論是速度還是位移，其爆破振動的響應規律較為一致，且在坡面和坡腳處因應力波在邊坡自由面反射容易產生一定區域的振動加強場。

（3）在巖質邊坡爆破作用影響下，無論是拉應力還是壓應力其最大值均出現在坡腳附近。

（4）在實際的邊坡爆破開挖過程中，對邊坡的坡面，尤其是坡腳處應該加強保護措施。

參考文獻：

[1]Aysilio E，Conte E，Dente G.Seismic stability analysis of reinforcedslopes[J].Soil dynamics and earthquake，2000，19（3）：159-172.

[2]Spyros Sklavounos，FotisRigas.Computer simulation of shock wavestransmission in obstructed Terrains[J].Journal of Loss Prevention inthe Process Industries，2004，（17）：407-417.

[3]Siyahi，Bilge G.Pseudo-static stability analysis innormally consolidated soil slopes subjected to earthquake[J].Teknik Dergi/Technicaljournal of Turksih chamber of civil enginers，1998，9（DEC）：457-461.

[4]UDEC（Universal Distinct Element Code）user' s manual Version 3.0[M].Lundon：Itasca Consulting Group，Inc.，1996.

[5]蔣楠，周傳波，平雯，等.巖質邊坡爆破振動高速度高程效應[J].中南大學學報：自然科學版，2014，45（1）：237-243.

[6]唐海，李海波，蔣鵬燦，等.地形地貌對爆破振動波傳播的影響實驗研究[J].巖石學與工程學報，2007（9）：1817-1823.

[7]唐海，李海波.地形地貌對爆破振動波傳播的影響實驗研究[J].巖石力學與工程學報，2007（09）：1817-1823

[8]言志信，蔡漢成，王群敏，等.縱波作用下邊坡動力響應[J].工程地質學報，2010，18（4）：487-505.

[9]祁生文，伍法權.邊坡動力響應規律研究[J].中國科學E輯技術科學，2003，33（s）：28-40.

[10]何錚，徐衛亞，石崇，等.順層巖質高邊坡地震變形破壞機制三維數值反演研究[J].巖土力學，2009，30（11）：3512-3518.

[11]陳明，盧文波，李鵬，等.巖質邊坡爆破振動速度的高程放大效應研究[J].巖石力學與工程學報，2011（11）：2189-2195.

[12]李鵬，蘇生瑞，王閆超，等.含軟弱層巖質邊坡的動力響應研究[J].巖土力學，2013（S1）：365-370，378.

[13]孟祥甜.露天邊坡動載響應特性的數值模擬研究[D].包頭：內蒙古科技大學，2015.

[14]宋光明，陳壽如，史秀志，等.露天礦邊坡爆破振動監測與評價方法的研究[J].有色金屬，2000（4）：24-27.

[15]王在泉，陸文興.高邊坡爆破開挖振動傳統規律及質量控制[J].爆破，1994，11（3）：1-4.

[16]夏詳，李俊如，李海波，等.爆破荷載作用下巖體振動特征的數值模擬[J].巖土力學，2005，26（1）：50-56.

[17]Kyhlemeyer R L，Lysmer J.Finite Element Method Accuracy forWave Propagation Problems[J].Soil Mech & Foundations Div，ASCE，1973，99（5）：417-421.

[18]Josef Henrych.The Dynamics of Explosion and Its Use[M].NewYork：Elsevier Scientific Publishing Company，1979.

[19]S.G.Chen，J.Zhao.UDEC modeling of a field explosion test[J].International Journal of Blasting and Fragmentation，2000（4）：149-163

[20]Josef Henrych.The Dynamics of Explosion and Its Use[M].NewYork：Elsevier Scientific Publishing Company，1979.

引用本文：唐旭，方正峰，鄒飛.基于FLAC3的巖質邊坡爆破動力響應規律研究[J].人民長江，2019，50（3）：198-204.

Study on dynamic response laws of rock slope blasting based on FLAC3D

TANG Xu'，FANG Zhengfeng2，ZOU Fei，4

（1.Guizhou Province Quality and Safety Traffic Engineering Monitoring and Inspection Center Co.，Ltd.，Guiyang 550081，China;2.Guizhou Hongxin Chuangda Engineering Detection & Consultation Co，Ltd.，Guiyang 550014，China;3.China GuizhouTransportation Planning Survey & Design Academe，Guiyang 550081，China;4.School of Ciwil Engineering，Central South University，Changsha 410000，China）

Abstract：The dynamic stability of slope has always been the focus of geotechnical engineering and seismic engineering.Inthis paper，FLACED numerical calculation method is used to simulate the vibration velocity，displacement and stress of rocky slopeunder blasting action.And on the basis of comparing and verifying the peak value of blasting vibration，the dynamic responselaws of rocky slope was analyzed.The results show that the seismic wave has a strong directionality and propagates mainly to thepositive direction of the applied load.On the slope surface and at the foot of the slope，it is easy to produce the vibrationstrengthening field in a certain area due to the reflection of the force wave on the free surface of the slope.The maximum value ofstress，whether tensile stress or compressive stress，appears near the slope foot.In the actual blasting excavation，the slope surface should be protected，especially the slope foot.The research results have certain reference for the construction design of rockyslope excavation.

Key words：dynamic response;rock slope;FLAC3D;blasting