基于網格密度峰值聚類的實時雷達分選系統

顧軍華 田 喆 蘇 鳴 張亞娟

(河北工業大學人工智能與數據科學學院 天津 300401)(河北省大數據計算重點實驗室 天津 300401)

0 引 言

雷達分選是雷達信號處理中的重要一環，只有從交疊的雷達數據中分解出每個雷達的數據，才能對雷達數據進行準確分析，因此雷達分選的準確性直接影響了雷達的性能。隨著雷達的廣泛應用，雷達所處的電磁環境日益復雜[1]，單純依靠脈沖重復周期(PRI)的分選系統已經無法滿足人們對雷達分選準確度的需求。近年來，有學者提出基于聚類的雷達分選系統[2]，這類方法無須先驗信息，可以處理嚴重重疊的雷達數據。針對雷達分選系統的實時性要求，實際應用中常采用數據流聚類算法進行分選。

CluStream算法是最早出現的數據流聚類算法，該算法包含在線和離線兩個階段，這種高效的框架成為了數據流聚類的主流框架。CluStream算法存在只能發掘球狀類、不能識別噪聲點等問題，為了解決上述問題，提出基于網格的數據流聚類算法(D-Stream算法)，該算法通過將數據點映射到網格，提升了算法效率。此后，出現了大量對D-Stream算法的改進[3]，其中ExCC算法[4]按照每個維度的特性分配各個維度的粒度來劃分網格，并且在線階段考慮了數據流流速，具有很好的效率。但是上述基于網格的數據流聚類算法，存在著容易丟失聚類的邊界和容易將距離較近類合并的問題。

針對上述兩個問題，本文提出了基于網格密度峰值的數據流聚類算法(GDP-Stream)。該算法首先于在線階段采用一種新的雙重網格劃分方式來建立概要數據結構，極大地減少了聚類邊界丟失的概率。其次，鑒于密度峰聚類算法(DPC)[5]可以很好地區分距離較近的類，因此本文算法通過在離線階段融入改進的DPC算法，來避免傳統網格合并方法容易將距離較近的類合并的問題。為了證明GDP-Stream算法可以有效地進行雷達分選，本文將GDP-Stream算法、ExCC算法和DP-Stream算法[6]在仿真雷達數據集上進行對比實驗。其中，DP-Stream算法是一種基于DPC的數據流聚類算法。結果表明，GDP-Stream算法相比于ExCC算法和DP-Stream算法有著更高的準確度和抗干擾能力。

1 GDP-Stream算法

GDP-Stream算法的框架如圖1所示。

圖1 GDP-Stream算法框架圖

在線階段，不斷接收數據流，采用雙重網格劃分生成并維護概要數據結構。當收到用戶發來的聚類請求時，算法進入離線階段，執行基于改進DPC算法的網格合并，生成聚類結果。

1.1 在線階段

數據流樣本集X={X1,X2，…，Xn}是由n個有d維屬性的數據樣本點Xi={Xi1,Xi2，…，Xij，…Xid}組成的，Xij為X中第i個樣本點的第j維屬性。數據空間的上界M={M1,M2，…，Md}，下界m={m1,m2，…，md}，其中Mi=max(X1i,X2i，…，Xni)，mi=min(X1i,X2i，…，Xni)。

定義1(靜態網格) 由數據空間對每一維k等分得到。網格邊長l={l1,l2，…，ld}。靜態網格Gi的密度DGi為靜態網格中包含的數據點數量。當靜態網格密度大于用戶設置的密度閾值DT時，稱該靜態網格為高密度靜態網格，否則稱低密度靜態網格。

定義2(數據樣本點之間的距離) PDW中不同屬性的量綱差別很大[7]，為避免影響聚類準確性，本文對歐式距離進行min-max歸一化改進，數據樣本點Xi和Xj的距離如下所示：

(1)

傳統網格聚類算法多采用靜態網格劃分。網格數量隨數據維數增長而激增，降低了算法的效率。并且這種劃分直接丟棄低密度網格中的點，容易丟失聚類的邊界。本文基于文獻[2]進行改進，提出雙重網格劃分，該方法有效濾除了噪聲點，并在下文的網格合并過程中只對動態網格進行操作，由于動態網格數量不隨維度一起增長，提高了效率。

定義3(動態網格) 以Xi點為網格中心，定義1中的網格邊長l為邊長創建的網格稱為動態網格。以Xi點為中心的動態網格的密度DXi為動態網格中數據點的個數。

當有數據點屬于兩個動態網格，則稱這兩個動態網格相交。如圖2所示，求一個動態網格的相交動態網格時，只需搜索與該動態網格中心點所在靜態網格相鄰的靜態網格即可。

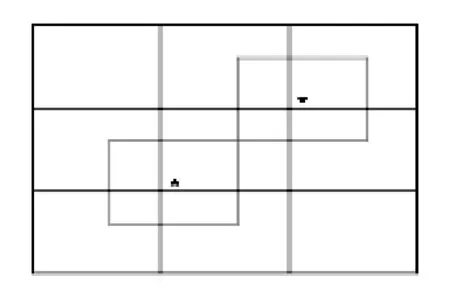
圖2 相交動態網格

對數據流X={X1,X2,…,Xn}執行雙重網格劃分，生成并維護概要數據結構的具體步驟如下：

(1) 設置參數：噪聲過濾閾值DT、靜態網格劃分份數k、數據點最大數量max_X。

(2) 積累一定的數據點，計算X的上界M和下界m，根據靜態網格劃分份數k，計算網格邊長l。

(3) 進行靜態網格劃分，將數據空間k等分。

(4) 從數據流X接收一點Xi，存入X_list。

(5) 若X_list中數據點總量達到max_X，則刪除最早到達的數據點，如果該數據點所處的靜態網格退化為低密度靜態網格，則刪除該靜態網格中包含的動態網格。

(6) 求Xi所屬靜態網格Gi，更新DGj。

(7) 如果DGj由低密度靜態網格轉變為高密度靜態網格，則執行(8)，否則執行(10)。

(8) 對Gj中每一個數據點，判斷該點能否落入某個已存在的動態網格中。若能，則將該點存入該動態網格中；若不能，則以該點為中心，根據網格邊長創建一個新的動態網格。

(9) 判斷與Gj相鄰的低密度靜態網格中的每個點能否落入(8)中新創建的動態網格，若能則存入。

(10) 若X中有數據點未處理，則執行(4)，否則在線階段結束。在線階段，得到一組靜態網格和動態網格，作為概要數據結構。

如圖3所示，雙重網格劃分可以很好地處理靜態網格劃分存在的聚類邊界丟失問題。

圖3 網格劃分對比

1.2 離線階段

離線階段對在線階段生成的概要數據結構(靜態網格和動態網格)執行網格合并。

按照傳統的網格合并思路，直接合并相交的動態網格，可以高效地處理復雜形狀類，如圖4所示。

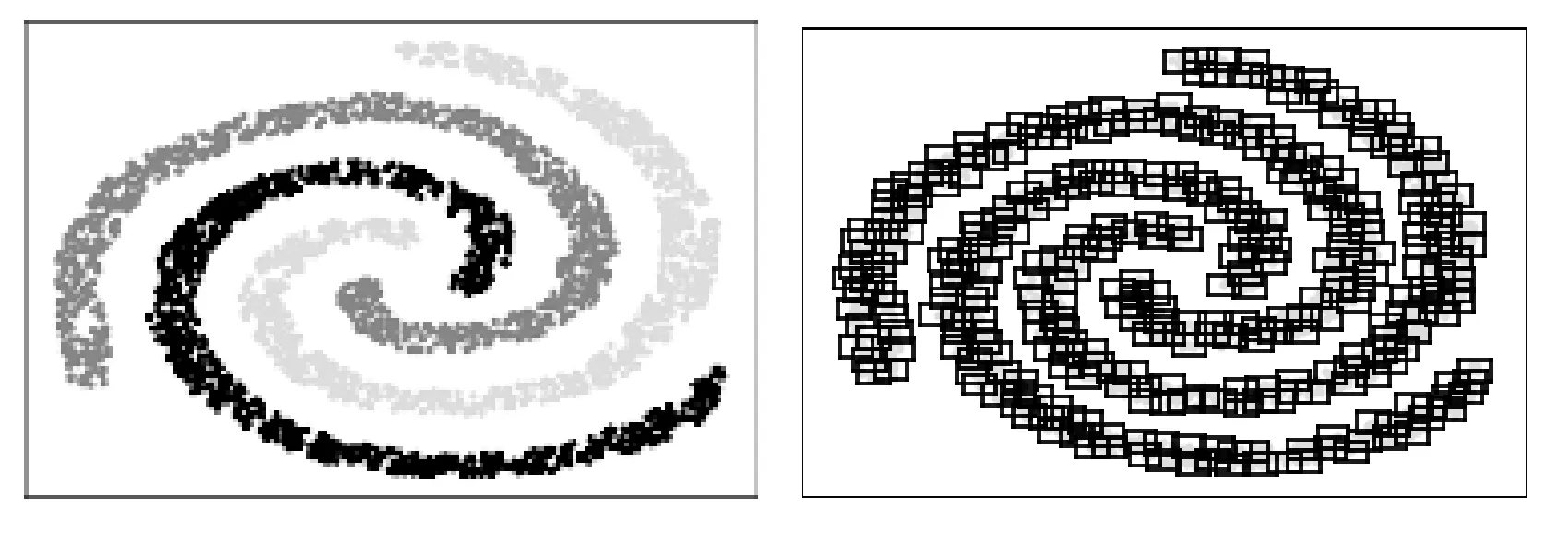
圖4 傳統網格合并

但是這種合并方式只考慮了局部信息，缺乏對數據空間的整體考量，如果兩個類距離較近，很可能被合并為一類，如圖5所示。

文獻[5]提出DPC算法，該算法的思想是首先求出密度峰作為聚類中心，密度峰為本身局部密度大并且與其他局部密度更大數據點的距離較大的點；然后將其他數據點歸類到相應的密度峰。DPC算法對聚類中心的挖掘，考慮了數據空間的整體特性，可以很好地區分距離較近的類[8-10]。參考DPC算法中密度峰的定義，密度峰動態網格的定義如下：

定義4(密度峰動態網格) 當動態網格擁有較高密度，且與其他密度更大的動態網格之間的距離較大，稱其為密度峰動態網格。本算法采用文獻[11]中的密度峰指標ZXi如下：

(2)

式中：dmXi為以Xi為中心的動態網格與更高密度動態網格之間的最小距離：

ZXi=DXi×dmXi

(3)

首先計算所有動態網格的ZXi，排除ZXi最大的動態網格，對于剩下動態網格排序后的序列為Z={Z1,Z2，…，Zm}，其中m為ZXi值不為最大值的點的動態網格數量。

I=argmaxi((Zi-1-Zi)-(Zi-Zi+1))

(4)

稱{Z1,Z2，…，ZI}所對應的動態網格為密度峰動態網格。

但是DPC算法有著效率低的缺點，并且容易把復雜形狀的類劃分為多個類。不能將DPC算法中的方法直接用于本文對動態網格的合并，因此本文對DPC算法思想提出如下改進。

改進1：降低挖掘密度峰動態網格的時間消耗。

定義5(密度極大動態網格) 當動態網格密度不小于它的任意一個相交動態網格密度，且大于所有動態網格平均密度，稱該動態網格為密度極大動態網格。

密度極大動態網格的ZXi較大，密度峰動態網格大多存在于密度極大動態網格中。求得密度峰動態網格的時間復雜度為O(m2)。為了提高效率，本算法首先用O(m)的復雜度求得密度極大動態網格，再從所有密度極大動態網格中求得密度峰動態網格。

改進2：降低非密度峰動態網格歸類時間消耗。

定義6(動態網格集) 對于以Xi點為中心的密度峰動態網格，稱以它為基礎歸類得到的動態網格集為CXi。

如果按照DPC算法中思想進行歸類，對于每個非密度峰動態網格，將它按密度降序的順序歸類到密度大于它且距離最近的動態網格所屬的類中，得到動態網格集。

本算法改進的歸類方法如下：首先將所有動態網格按密度降序排序，之后按順序進行歸類。對于非密度極大動態網格，因為一定存在密度大于它的動態網格與它相交，相交的動態網格之間的距離一定小于不相交的，所以只需搜索與它相交的動態網格，從中找到密度大于它且距離最近的動態網格，即為所求。上文中提到，求相交動態網格相比于求距離最近動態網格只需要很少的時間，所以歸類的效率得到了很大的提高。對于密度極大動態網格，無法快速求解，因此按照DPC算法的方法求解。但是由于密度極大動態網格數量較少，所以時間損耗不大。

改進3：避免復雜形狀類被劃分為多個類。

復雜形狀的類會存在多個密度峰，DPC算法會把非密度峰點歸類到密度峰所屬的類，所以容易導致復雜形狀的類被錯誤的劃分為多個類[8]。

為解決該問題，本文引入了相似度。通過觀察發現，同一個類中的動態網格應該具有相似的密度；若相鄰動態網格集屬于同一類，則它們之間相交動態網格的平均密度不會與它們兩個的平均密度差距很大。則相似度定義如下：

定義7(相似度) 動態網格集CXi和CXj之間的相似度為：

(5)

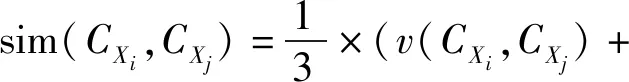
(6)

式中：d(CXi)為CXi中動態網格的平均密度。式(5)為相對密度差，當sim(CXi,CXj)超過一定閾值SIMT后判定兩個動態網格集相似，合并CXi和CXj。

基于改進DPC算法的網格合并的步驟如下：

(1) 設置相似度閾值SIMT。

(2) 將所有動態網格，按照密度從大到小排序。

(3) 找到所有密度極大動態網格。

(4) 從密度極大動態網格中找到密度峰動態網格。

(5) 對所有非密度峰動態網格進行歸類，生成一組動態網格集。

(6) 對于每兩個相交動態網格集CXi和CXj，當sim(CXi,CXj)≥SIMT時，合并CXi和CXj。

(7) 將動態網格聚類結果，映射到數據點。當數據點屬于多個不同類動態網格時，將其歸屬于距離最近的動態網格所屬的類。

2 仿真實驗分析

2.1 雷達信號仿真

脈沖描述字(PDW)流的生成流程如下：

(1) 單部雷達PDW流產生：PDW中脈沖載頻(RF)、脈沖寬度(PW)以及脈沖到達角(DOA)三個屬性最為穩定，常用來作為雷達分選系統的依據。脈沖重復周期(PRI)屬性，用來計算每個脈沖的到達時間(TOA)。因此，本文的雷達信號需要對上述四個屬性進行仿真。其中，PW誤差為1%；DOA誤差為2°；RF分為固定、捷變、跳變，誤差為1%。TOA由下式確定:

TOAn=TOAn-1+PRI+ω

(7)

式中：PRI分為固定、抖動、參差和滑變，TOA0為脈沖初始到達時間，誤差ω為PRI的1%。

(2) 干擾脈沖數據流產生：在真實的電子偵察活動中，會有噪聲數據進入雷達分選系統。本文通過在隨機時刻加入處在數據空間值域內的偽隨機數來模擬干擾脈沖。

(3) 排序處理：多部雷達的PDW流產生后，需要將多個脈沖序列依照TOA排序融合成一個脈沖序列，從而得到整個PDW流。

(4) 重疊處理：當某一脈沖的到達時間小于前一脈沖的結束時間，就會出現不同雷達脈沖在時域上重疊的現象。當發生脈沖重疊時，本文按照5%的概率進行了丟失處理。

仿真實驗模擬了4部不同類型雷達的PDW流。同時加入了雷達脈沖總數10%的干擾脈沖，具體參數設置如表1所示。圖6為數據點分布圖。

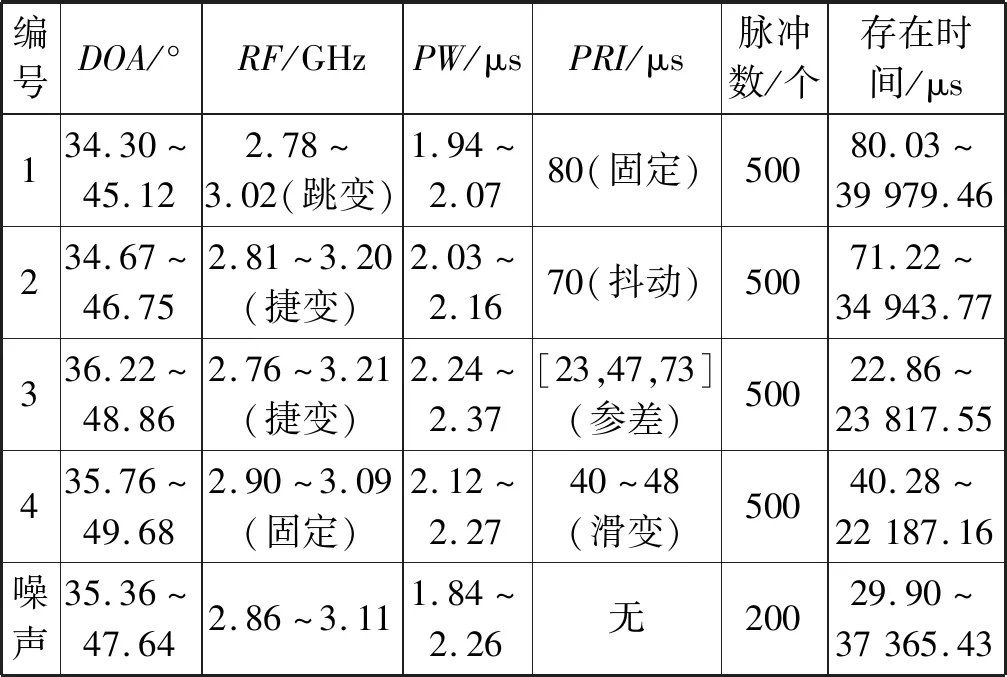
表1 實驗數據參數表

(a) 數據點三維分布圖

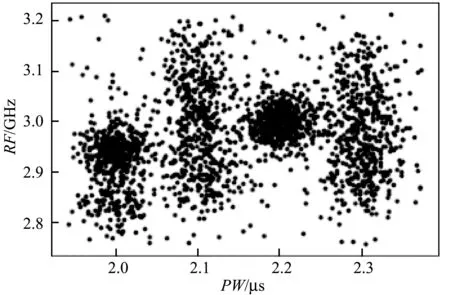
(b) 含噪聲數據點PW-RF分布圖圖6 數據點分布圖

由圖6可以看到4部雷達的脈沖載頻RF、PW以及脈沖到達角DOA三個屬性都嚴重重疊在一起，可以用來檢驗雷達分選系統在復雜信號環境中的有效性。

2.2 實驗結果分析

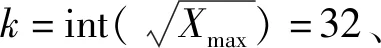
為了觀察GDP-Stream算法求得密度峰動態網格的效果，在T1=7 152.59 μs(第500個數據點到達時刻)、T2=10 700.87 μs(第750個數據點到達時刻)和T3=14 255.53 μs(第1 000個數據點到達時刻)分別求得密度峰動態網格。如圖7所示，為了方便觀察，將密度峰動態網格投影到PW-RF平面。可以看出GDP-Stream算法在T1和T2時刻比較準確地求得了每個類的密度峰動態網格，T3時刻由于類內密度的暫時變化，導致該時刻求得的密度峰動態網格數量過多，但是由于GDP-Stream算法會合并相似度超過SIMT的相鄰動態網格集，因此過多的密度峰動態網格數量并不會影響聚類質量。

圖7 密度峰動態網格圖

本文采用聚類準確度(CA)作為聚類效果的評價標準，它表示正確聚類的數據點數占總數據點數的比例，計算方法如下：

(8)

式中：n代表總數據點數，|Cj∩Pk|表示屬于第k聚類并且屬于真實分組第j組的記錄數目。準確度在[0,1]內，準確度越大表示聚類效果越好。

為了說明GDP-Stream算法的有效性，本文分別把GDP-Stream算法與ExCC算法以及DP-Stream算法(參數設置見文獻[4]、文獻[6])在多個時刻的聚類準確度進行對比。如圖8所示，GDP-Stream算法和DP-Stream算法相比于ExCC算法，有著更好的聚類準確度，這是因為GDP-Stream算法采用動態網格劃分方式，會產生聚類邊界丟失問題。而DP-Stream算法則由于直接采用DPC算法的思路所以不容易丟失聚類邊界。在大多數時刻GDP-Stream算法聚類準確度好于DP-Stream算法，這是因為單純使用DPC算法的聚類方法，會導致復雜形狀的類被劃分成多個小類。

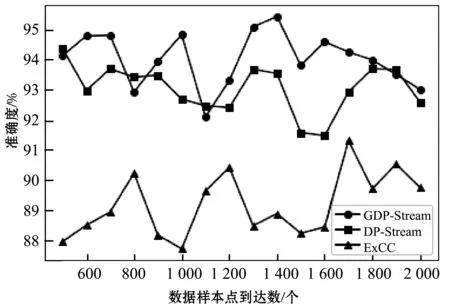
圖8 實驗結果對比圖

3 結 語

本文針對日益復雜的電磁環境，提出一種基于網格密度峰值聚類的實時雷達分選系統，該算法將基于網格的數據流聚類算法和DPC算法的優點融合，并在準確度和效率上加以優化。通過仿真實驗證明，本文算法可以在雷達信號嚴重重疊并且存在干擾的電磁環境中，進行高效、準確的雷達分選。