高端養老機構服務的價格形成能夠提高社會福利嗎？
——基于Hotelling動態博弈模型的分析

（上海工程技術大學 社會科學學院，上海 201620）

人口老齡化背景下，我國養老服務業發展迅速。據統計，截至2017年底，全國各類養老服務機構15.5萬家，比上年增長10.6%。然而，隨著人們物質和精神生活水平的不斷提高，我國養老服務數量和質量的需求日益增長，僅依靠公辦養老機構會使政府財政不堪重負，因而亟需大力發展民辦養老機構。近年來，在一些經濟發達的大城市，出現越來越多的高端民辦養老機構。根據中國養老信息網，截至2017年底，全國高端民辦養老機構（每人每月養老服務費大于1萬元）共26家，提供11 202張床位，其中有3家高端養老機構歸屬L集團旗下，4家高端養老機構歸屬T集團旗下。然而，相對于養老金及積蓄足以支付高端養老機構收費的龐大退休老年人群體，我國高端養老服務市場供給顯得嚴重不足，而且目前在高端民辦養老機構供給側存在一定的壟斷性，不利于高端養老服務市場的健康發展。此外，筆者實地調研發現，目前，高端養老機構一般是以某保險集團旗下子公司的形式存在的，因此老人入住高端養老機構一般有兩種支付方式，一種是躉交“押金”入住，即退休后一次性繳納一定的押金入住該高端養老機構，同時每月支付一定的養老服務費用即可；另一種是購買“免押金”保險入住，即老人在退休前購買某保險公司的“免押金”保險，每月支付一定的保險服務費用，退休后毋須繳納押金即可入住指定的高端養老機構，僅需支付每月的養老服務費用即可，而這種“免押金”保險可以看成是一種養老金儲蓄計劃。因此，思考如何打破高端養老服務市場的壟斷格局，提高整體社會福利，促進高端養老服務市場健康發展，已經成為當下亟需解決的重要問題。

國外學者關于養老服務定價的研究主要分為兩大類。第一類為完全信息條件下的定價，Arrow等[1]認為公共事業服務價格必須等于邊際成本，但Zamparelli等[2]認為邊際成本定價只是一種理想的定價方式，若長期以邊際成本進行定價，會使服務機構收不抵支，因此他主張使用平均成本定價，其價格高于邊際成本。第二類為不完全信息條件下的定價，Kanemoto[3]認為民辦養老機構在發展過程中必然形成寡頭壟斷，由此，基于兩步定價法可求得養老服務價格的Bertrand均衡解；Forder等[4]在比較了歐洲各國民辦養老機構的服務價格后，認為英國的民辦養老機構在對養老服務定價時會優先考慮養老服務質量；Sugawara[5]證明了日本民辦養老機構普遍采用的租金預付定價模式存在著缺陷，不利于民辦養老機構有效地抵御長壽風險。相較于國外的研究，雖然我國關于養老服務定價及社會福利問題的研究起步較晚，但近年來已產生諸多有價值的成果。關于民辦養老機構的定價機制研究，席群等[6]分析了江蘇省南通市的機構養老服務供需現狀，發現老人的收入顯著影響養老服務價格；王希晨等[7]基于PEST模型分析了影響我國民辦養老機構定價的宏觀因素，認為在價格制定過程中，雖然政治、社會環境能顯現優勢和機會，但在經濟、技術環境方面面臨巨大阻力。

基于已有的研究成果，筆者認為雖然高端養老服務屬于私人物品，購買高端養老服務也應該是一種市場行為，但由于目前高端養老服務機構處于壟斷地位，老人處于相對弱勢地位，在此情形下，為了保障老人的基本權益，既需要考慮市場性，又需要兼顧社會性。因此，需要將整體的社會福利效應列入考慮范圍。同時，結合本文的研究結論，筆者發現無論老人選擇怎樣的方式入住，高端養老服務機構均能獲得超額利潤。不同的是，老人選擇躉交“押金”入住時，老人的福利受損，機構雖有所盈利，但整體的社會福利不高，不利于高端養老服務機構的長期發展；當老人選擇購買“免押金”保險入住時，機構盈利增加，老人福利和社會福利也增加，有利于高端養老服務機構健康可持續發展。

1 定價均衡模型引入

本文參考了楊渭文等[8]的建模思想，構建了兩期Hotelling動態博弈模型，以期探討兩種入住方式下的定價機制和社會福利。鑒于此，需要以下基本假定。

假定1：在微觀經濟學建模中，為便于分析，常用一維的線段抽象地表示競爭性企業（商戶）的空間經濟地理特征。由此，首先假定在線段長度為1的高端養老服務市場中，存在兩家具有理性預期和信息對稱的保險集團，旗下分別設立了兩家高端養老服務機構A，B。它們位于該線段兩側（A機構位于左側，B機構位于右側），約定不進行惡性低價競爭。

假定2：A，B兩家高端養老服務機構提供的養老服務是有差別的，且提供的服務可覆蓋整個市場，同時規定兩家機構的“免押金”保險服務的邊際成本均為C1元，養老服務的邊際成本（護理人員工資、管理人員工資和床位費）均為C2元。

假定3：在該市場中，均勻分布著退休后需要入住養老機構的老人。這些老人都具有以下特征。a.老人都具有理性預期，在選擇養老機構時，完全依據自己的理性判斷和行為偏好，因此老人的決策是相互獨立的；b.老人對這兩家養老機構的初始評價均為U，且U足夠大，說明每個老人退休后都會入住養老機構，整個高端養老服務市場將被完全覆蓋；c.無論老人選擇哪家養老機構，都存在一定的距離成本，設單位距離成本為d。

假定4：在老人退休前（博弈第一期），兩家機構均推出了購買“免押金”保險入住計劃，老人只要繳納P1i元的保險費（i=A,B）就可以免押金入住養老機構，且老人購買和退出“免押金”保險是完全自由的。同時，兩家養老機構均告知老人，如果退休前在本機構購買“免押金”保險，退休后入住本機構將享受養老服務費元的承諾價格。在老人退休后（博弈第二期），如果沒有購買保險計劃，老人需繳納元的押金才能入住，且，同時兩家機構還規定了養老服務費元的實際價格，為吸引老人購買本機構的保險計劃，機構將收取老人入住后養老服務費中的較低者，通常。

2 定價均衡模型分析

根據兩期動態博弈模型及基本假定，分析兩家高端養老服務機構的定價均衡問題，需要先了解博弈第二期兩家高端養老服務機構所面臨的市場需求。由于老人具有不同的消費偏好和理性預期，養老機構i在博弈第二期所面臨的市場需求由兩部分消費群體構成：一部分是退休前購買“免押金”保險，退休后“免押金”入住的老人；另一部分是退休前未購買機構的“免押金”保險，退休后躉交“押金”入住的老人。對于這兩種情況，需要逐個分析老人的決策行為和養老機構的定價機制。為了方便分析，下文均以高端養老服務機構A為例。

2.1 躉交“押金”入住時的定價均衡

因為老人對兩家高端養老機構所提供的養老服務初始效用相同，所以若以點E為線段AB的中點，在點E左側的老人會入住A機構，在點E右側的老人會入住B機構。由于老人在整個養老服務市場中是均勻分布的，不妨設fa為機構A的選址位置，fb為機構B的選址位置[9]。因此，可求得養老機構A，B各自的需求函數QA，QB及fa，fb

由兩家養老機構的需求函數QA和QB，可求得各自的利潤函數π2A和π2B

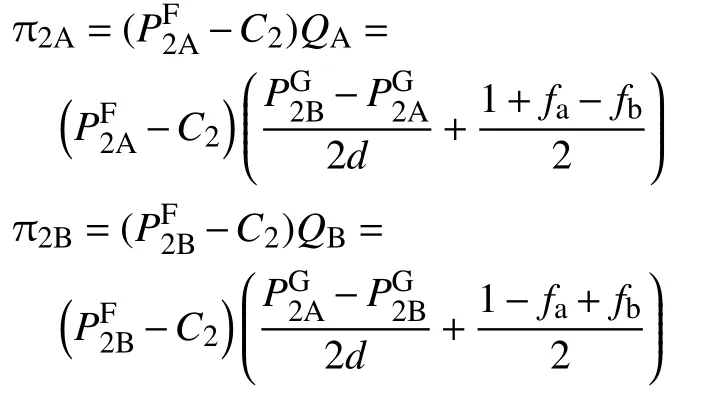
代入fa和fb，由利潤函數π2A和π2B的一階條件，可求得價格函數為

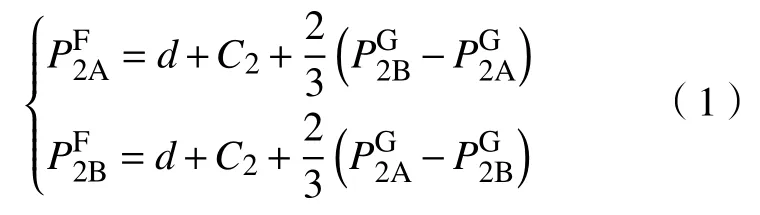
不難驗證π2A和π2B的二階偏導數均大于零，由此可以歸納出命題1。

命題1：在老人選擇“躉交押金入住”后，A，B兩家機構養老服務的均衡定價為。

命題1的經濟學意義：第一，從兩家機構養老服務的實際均衡定價可以看出，A，B兩家機構會在選址位置上進行位置博弈，并同時向市場中點E移動，在點E處開展背靠背競爭，尋求各自的利潤最大化；第二，在不降低養老服務質量的前提下，A，B兩家機構會根據養老服務的邊際成本確定其服務定價；第三，A，B兩家機構第二期的服務定價與第一期躉交押金有關，會根據對方收取躉交押金的數額確定其服務價格，具體表現在對方增加躉交押金后，機構會提高定價水平以增加利潤。

2.2 購買“免押金”保險入住時的第二期定價均衡

老人購買“免押金”保險入住時的第二期均衡定價研究方法與命題1的研究方法略有不同。因為兩家養老機構第二期的老人群體均由兩部分構成，即直接入住的老人和由另一機構轉移過來的老人。因此，不妨令la為第一期在A養老機構購買“免押金”保險入住的老人中，退休后仍選擇入住A養老機構的老人占第一期在A處購買保險的老人數量的比例，同理可令lb，則la與lb應滿足

式中，ω表示第一期老人購買A養老機構“免押金”保險的市場份額，代入式（3），由利潤函數π2A和π2B的一階條件，可得到各自的價格函數為

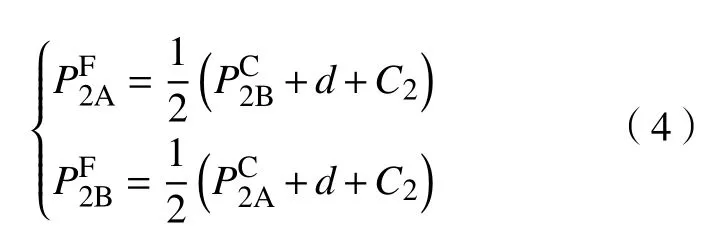
不難驗證π2A和π2B的二階偏導數均大于零，由此可得命題2。

命題2：在老人選擇購買保險免押金入住后，第二期A，B兩家養老機構可實現均衡定價：

命題2的經濟學含義：第一，A，B兩家養老機構的服務定價與對方的承諾價格密切有關。A機構在定價時，需參考B機構第一期對老人入住時的承諾價格；第二，整個養老服務市場實現均衡定價后，A，B兩家機構仍然會圍繞養老服務市場的中點E進行位置博弈；第三，不降低養老服務質量的前提下，A，B兩家養老機構會根據邊際成本來確定服務定價。

2.3 第一期購買“免押金”保險入住時的定價均衡

在分析老人第一期購買“免押金”保險入住的保險金額時，不僅要考慮兩家養老機構第一期的承諾定價和選址位置，還要考慮養老機構第二期的實際定價。因為ω表示養老機構A第一期的市場份額，也可認為ω為老人在[0,1]養老服務市場中的位置。由于老人的初始效用相同，假設老人第一期在養老機構A選擇購買“免押金”保險，如果老人第二期依然在[0,la]區間內，則就會選擇入住養老機構A，因此，老人第一期的期望效用為

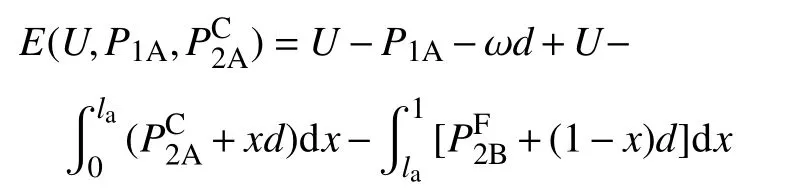
同理，可求得老人位于ω點選擇入住養老機構B的期望效用為

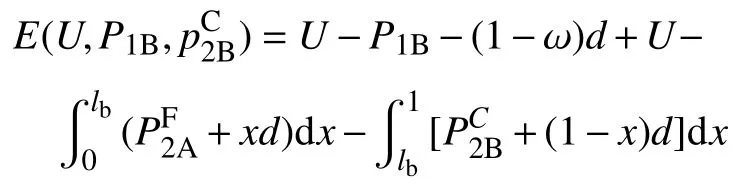
因為老人兩期的期望效用相等，不難求得

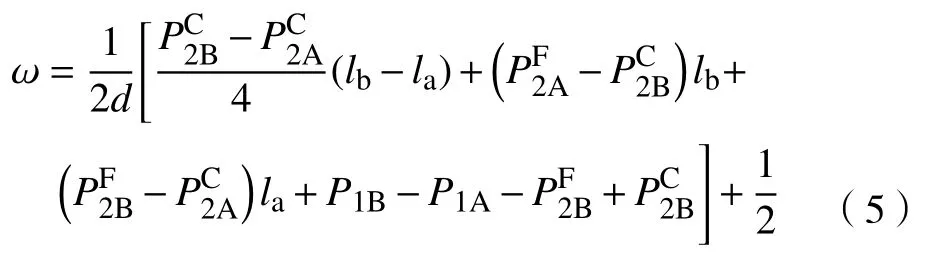
因此，第一期兩家養老機構的利潤函數為

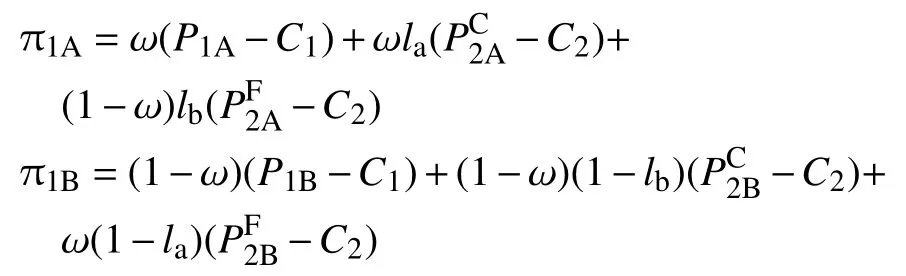
不難驗證π1A和π1B的二階偏導數均大于零，由此可以歸納出命題3。

命題3：A，B兩家養老機構在第一期的市場競爭中，存在唯一的子博弈精煉納什均衡解：。

命題3的經濟學意義：首先，第一期購買“免押金”保險的價格嚴格高于任意一期的邊際成本，即P1i＞C1，P1i＞C2，則在購買“免押金”保險入住的條件下，兩家養老機構第一期均能獲得超額利潤。若A，B兩家養老機構第二期均圍繞養老服務市場的中點E進行位置博弈，即當單位距離成本d→0時，第一期的保險服務價格仍然不低于任意一期的邊際成本，且?P1i/?C2=2(?P1i/?C1)，說明第二期兩家機構養老服務的邊際成本對第一期保險定價的影響顯著高于第一期保險服務自身的邊際成本對其價格的影響。換言之，老人是否購買“免押金”保險，主要參考第二期養老服務的成本和質量。同時，，說明養老機構第一期免押金保險的競爭程度會隨著單位距離成本的增加而增加，兩家養老機構出現“合謀”現象，造成社會福利的損失。

其次，第二期機構提供養老服務的承諾價格嚴格高于兩期邊際成本之和，即P2i＞C1+C2，說明若對老人實行養老服務的承諾價格，機構均能賺取超額利潤。同時，，說明機構養老服務的承諾價格會隨著單位距離成本的增加而下降，養老機構可采用較低的承諾價格來吸引老人第一期購買免押金保險，以增加第一期機構的市場份額。

最后，聯立命題2和命題3，不難求出第一期和第二期整體的子博弈精煉納什均衡解

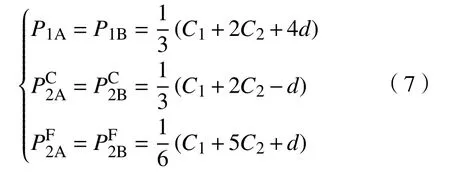
從式（7）來看，兩家養老機構第二期的養老服務價格均嚴格高于任意一期的邊際成本，即，說明第二期兩家養老機構都能獲得超額利潤。即使單位距離成本d→0，其價格仍不低于任意一期的邊際成本，且，說明雖然第二期養老服務的實際價格受到第一期邊際成本的影響，但影響程度遠不及第二期養老服務的邊際成本，因此養老機構主要參考第二期養老服務的邊際成本進行定價。

3 福利分析與比較

明晰A，B兩家高端養老服務機構的定價機制后，接下來分析兩種入住方式的社會福利。為了方便分析，本文的“社會福利”是指老人的消費者剩余與高端養老服務機構的生產者剩余之和。基于此，以下將重點比較躉交“押金”入住方式和購買“免押金”保險入住方式的社會福利。

3.1 躉交“押金”入住時的社會福利分析

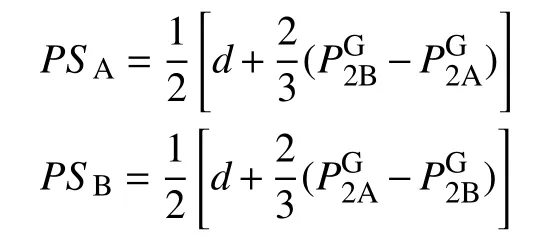
命題4：老人躉交押金入住養老機構，其消費者剩余TCS1→0，兩家養老機構的總生產者剩余隨著養老機構單位距離成本的增大而增大，社會福利TW1=TCS1+TPS1=d。

3.2 購買“免押金”保險入住時的社會福利分析

因為購買“免押金”保險入住養老機構需要分為兩期，故在分析其社會福利時也需要分兩期考慮，即分別考慮第一期和第二期的消費者剩余和生產者剩余。

3.2.1 兩期消費者剩余的分析

a.第一期消費者剩余的分析。無論是躉交“押金”入住，還是購買“免押金”保險入住，老人都在購買一種入住資格，且，不妨假設為老人購買入住資格時意愿支付的最高價格，P1A為老人購買入住資格時支付的實際價格。由命題2可知，第一期的消費者剩余應為第一期養老機構的市場份額與老人實際支付和意愿支付最高價格之差的乘積，即，則第一期入住A機構的老人的消費者剩余為

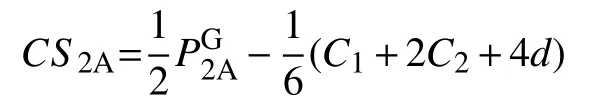
同理，可求得入住B機構的老人第一期的消費者剩余

b.第二期消費者剩余的分析。因為養老機構承諾價格與實際價格之間存在差價，即，老人第二期入住A機構的消費者剩余為

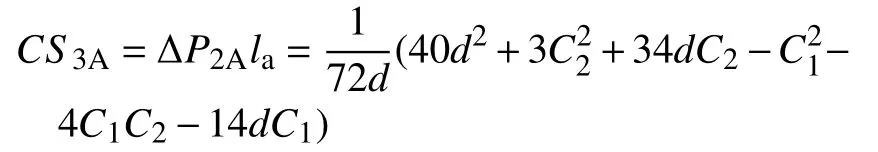
對式（8）中的C1和C2分別求偏導數，的增加而降低，會隨著養老服務邊際成本的增加而增加。對于購買“免押金”保險入住的老人，雖然沒有過多在意保險服務的質量和價格，卻比較重視第二期養老服務的質量，由于兩家養老機構相互承諾不進行惡性低價競爭，因此，伴隨養老服務質量的上升，養老服務的邊際成本也在提高。在此情況下，老人的總消費者剩余會明顯高于躉交“押金”入住時的總消費者剩余，即TCS2＞TCS1。

3.2.2 兩期生產者剩余的分析

a.第一期生產者剩余的分析。第一期的生產者剩余PS1A應為其第一期保險服務的經濟利潤。因此，第一期的生產者剩余為

綜上，老人購買“免押金”保險入住時的社會福利為：

因為總生產者剩余TPS3非負，而在此條件下，只有d＞3.2才能滿足，故不能滿足“同增”或“同減”的條件，故必然存在一期遞減、一期遞增的情況。由此可歸納出命題5。

命題5：選擇購買“免押金”保險入住時，高端養老服務機構的社會福利會隨保險服務邊際成本的增加而緩慢下降，隨養老服務邊際成本的增加而緩慢增加，且d＞3.2時，購買“免押金”保險入住的社會福利遠遠大于躉交“押金”入住的社會福利，即TW2＞＞TW1。

4 數值模擬分析

為了更加直觀地表述結論，筆者采用蒙特卡洛模擬數值法，運用Matlab軟件調用random函數隨機產生30組偽隨機模擬數值，并利用這些數值檢驗本研究的結論。因為d＞3.2，且要滿足CS2＞0，TW2＞0，為方便計算，假定d=4，。

4.1 老人躉交“押金”入住時的相關變量

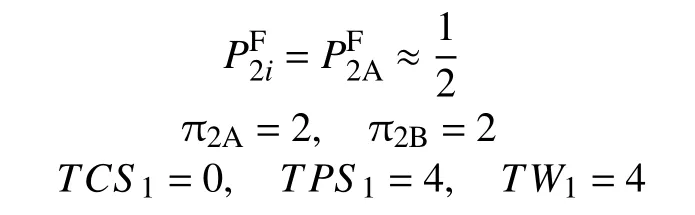
4.2 老人購買“免押金”保險入住時的相關變量

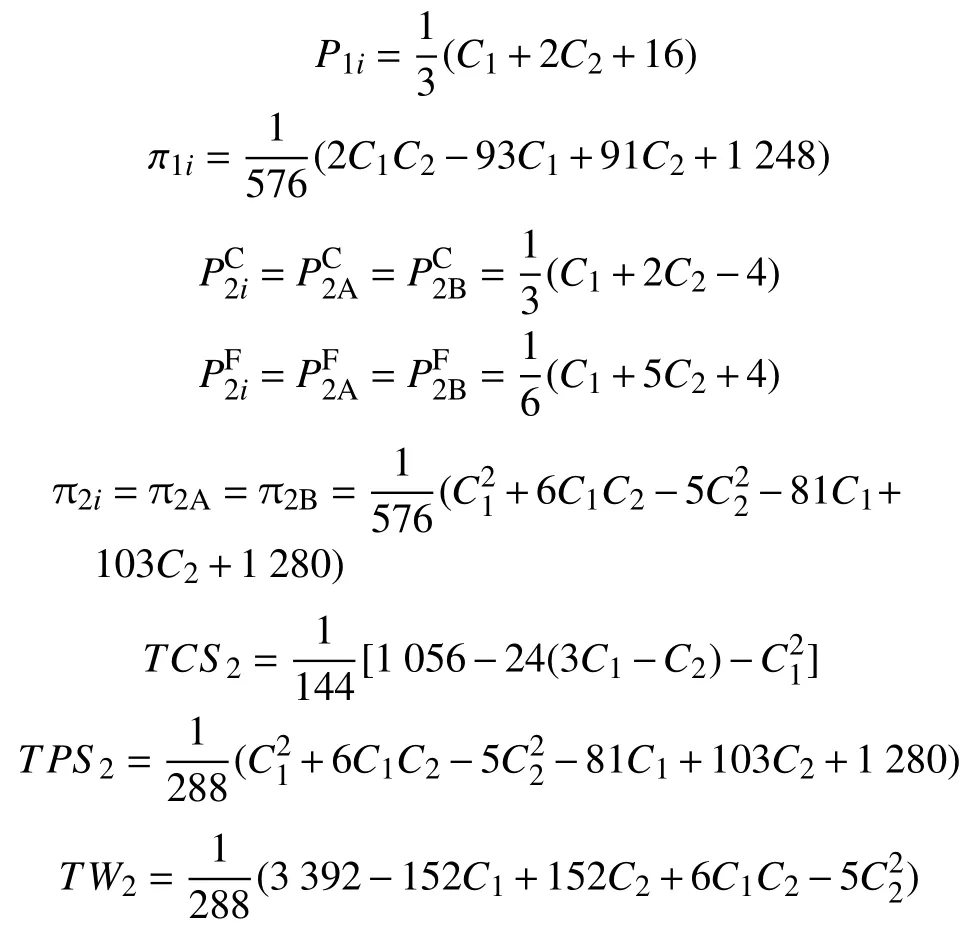
由于老人以躉交“押金”的方式入住養老機構，總生產者剩余TCS1=0，社會福利TW1=4均為常數，與C1，C2的大小無關，故本文略去其圖形分析。圖1和圖2分別為老人購買“免押金”保險入住的總消費者剩余和社會福利，能夠反映C1，C2與購買“免押金”保險入住的總消費者剩余、社會福利之間的關系，可以驗證上述模型的基本結論：

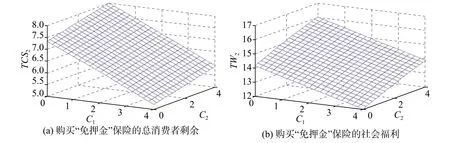
圖1 購買“免押金”保險的社會福利分析Fig.1 Social welfare analysis of purchasing "deposit-free" insurance

從圖1可以看出，購買“免押金”保險入住條件下，無論是總消費者剩余，還是社會福利，均表現為隨著第一期保險服務的邊際成本增加而遞減，隨第二期養老服務的邊際成本增加而增加，均顯著高于躉交“押金”入住條件下的總消費者剩余和社會福利。

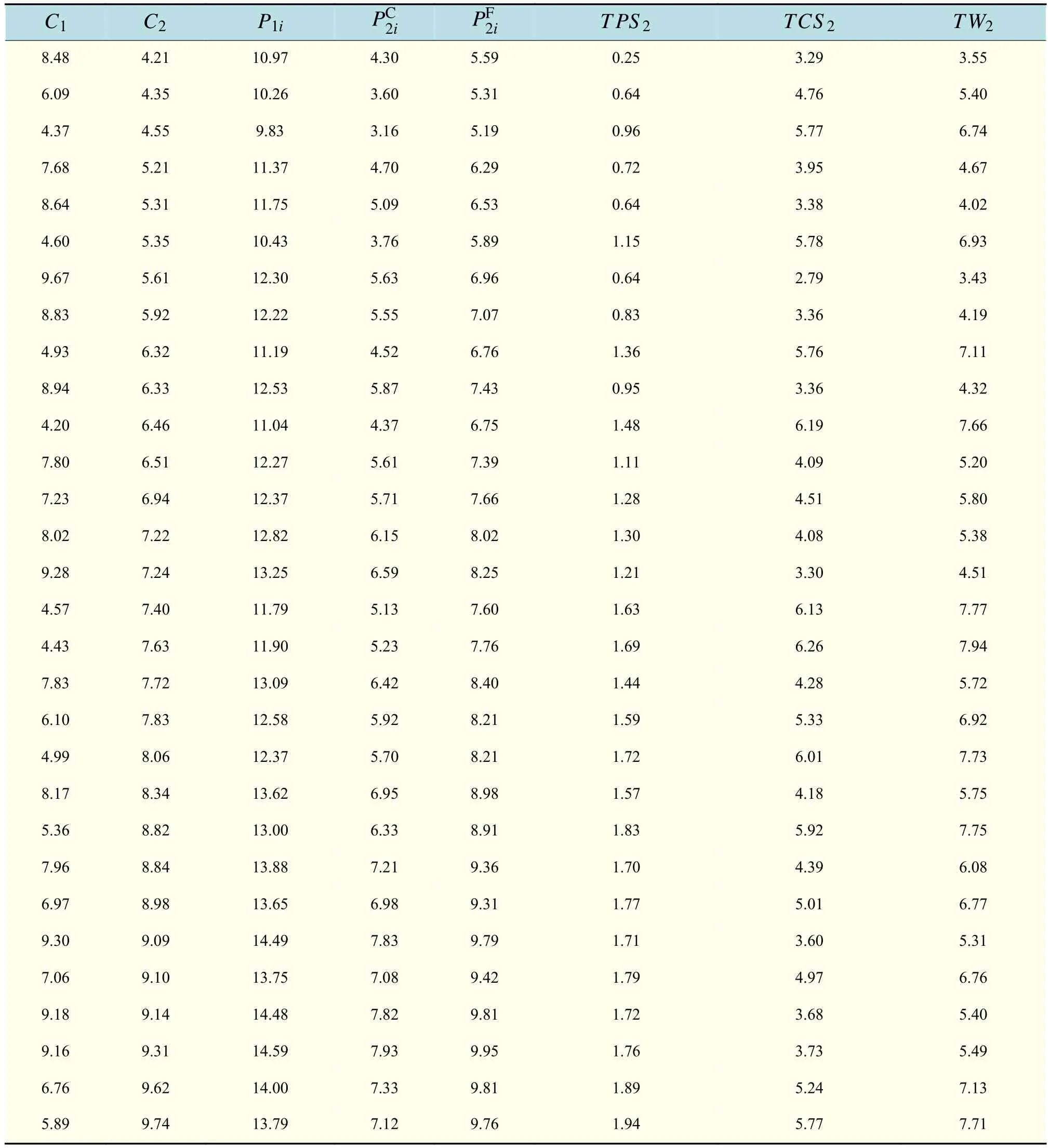
表1 “購買免押金保險入住”變量的數值分析表Tab.1 Numerical analysis table of variables in “Buying Deposit-free Insurance Accommodation”

第一，躉交“押金”入住的條件下，無論機構提供的養老服務定價如何，整體的社會福利都不會增加，在此情況下，兩家機構必會陷入“囚徒困境”，此時養老機構的利潤只與老人在高端養老服務市場中的位置有關，但此時老人的消費者剩余沒有相應增加，整體社會福利不變，因此，此定價機制不利于高端養老服務市場的健康發展。

第二，從表1可見，購買“免押金”保險入住條件下，在C2∈[4,10]時，老人的消費者剩余和機構的生產者剩余均呈現平穩的波動，整個養老服務市場處于良性狀態，社會福利有所提高。在C1∈[4,10]，C2∈[4,10]時，養老機構必然選擇C1=5.89，C2=9.74時的定價，即P1i=13.79，此時養老機構實現利潤最大化；對于價格管理部門或入住老人，必然選擇C1=4.43，C2=7.63時的定價，即，此時老人的消費者剩余和社會福利達到最大化。由此可見，高端養老服務機構推出“免押金”保險以吸引老人入住，可提高整體的社會福利，從而使高端養老服務市場良性運轉。

5 結論與建議

以雙寡頭高端民辦養老機構為研究對象，建立了兩期動態博弈模型，考察了躉交“押金”入住和購買“免押金”保險入住兩種方式的定價機制及社會福利效應，得出以下結論：

a.由于兩家寡頭機構壟斷了高端養老服務市場，無論老人采用何種入住方式，兩家高端民辦養老機構均會獲得超額利潤；

b.躉交“押金”入住條件下，兩家高端養老機構必然會展開價格博弈，使得消費者剩余受損，但兩家機構的經濟利潤未見大幅增加，最終使得社會福利降低；

c.購買“免押金”保險入住條件下，消費者剩余明顯高于躉交“押金”入住時的消費者剩余，且表現為隨著保險服務邊際成本的增加而降低，隨著養老服務邊際成本的增加而增加，而養老機構不會提高第一期免押金保險服務的邊際成本而損失入住養老機構的“客源”，因此兩家機構均會提高服務質量以吸引老人入住。與此同時，雖然兩家養老機構第一期的生產者剩余有所降低，卻使第二期生產者剩余增加了，從而使得兩家養老機構的生產者剩余最大化，社會福利得到提高。因此，可以說“免押金”保險可以改善高端養老服務市場的社會福利。