基于等速線模型的一維黃土動荷載響應分析

王文麗，王蘭民

(中國地震局蘭州地震研究所,甘肅 蘭州 730000)

黃土作為一種特殊的巖土材料，由于其特殊的粉粒性、富鹽性、大孔性、欠壓密性、非飽和性的多孔隙弱膠結架空結構[1-3]，使得黃土具有較高的地震易損性[4-6]。在動荷載作用下其宏觀力學行為十分復雜[7-8]，因而構建黃土材料的震陷理論計算模型是一項相當困難的工作。就目前來看，對黃土震陷的研究大致可分為兩類。首先是基于試驗數據統計分析黃土震陷與土的物理力學性質間的經驗方法，如王蘭民等[9]建立了考慮物性參數、固結應力、振次和地震動應力等因素的西北黃土殘余應變的經驗計算公式；陳永明等[10]提出了利用土層剪切波速預測黃土場地震陷量的方法；栗潤德等[11]通過試驗研究，探討了黃土的動強度和震陷隨含水量的變化規律；王峻等[12-14]對原狀黃土的動荷載試驗研究表明，黃土的震陷與隨機地震荷載的卓越周期、峰值和持續時間相關；徐舜華等[15]通過試驗研究提出了不同動應力作用下的黃土震陷臨界含水量。總結這些成果可以發現，黃土的震陷是一個復雜的物理力學過程，會受到干密度、含水量、受力歷史以及震動荷載等多重因素的影響。第二類是基于微觀機理的半經驗方法，如鄧津等[16]應用黃土氣固表面原理，建立了應用微結構特征參數估算黃土震陷系數的半經驗公式；孫軍杰等[17-18]通過耦合孔隙比及壓縮量與應力比之間的定量統計關系，建立了計算地震動作用下黃土殘余應變(震陷系數)的數學估算模型。分析以上研究可以發現，經驗方法在研究和判斷黃土震陷時起到了重要作用，但受到試驗條件的限制，在力學狀態和邊界條件更為復雜的實際工程中其適用性有限；而基于微觀機理的半經驗理論模型由于其繁多的內變量參數極難通過試驗獲取使得其工程實用性大打折扣。就目前來看，使用宏觀理論方法對黃土震陷的研究鮮有報道[19-21]。在描述復雜條件下土體的應力應變行為時，基于“現象學”的宏觀理論模型具有獨特的優勢(相關參數易于獲取、適用于復雜力學狀態的工程問題)，這也是常規土力學中使用最為普遍的方法。因而，可以借鑒現有常規土力學中得到成功應用的理論模型，研究黃土在復雜荷載條件下的震陷特性。

根據先前的研究，表征土體受力歷史的前期固結壓力以及震動荷載頻率均是會影響到土體震陷的重要指標[9,14]。這表明，預測黃土震陷的理論模型需要充分考慮應力歷史以及加載速率的影響。在現有常規土力學的理論模型中，“等速線理論”能夠較好地描述這兩個因素對土體應力應變行為的影響[22-23]。在該理論中，不同加載速率條件下的應力應變曲線為一系列平行線，即：在發生相同應變的情況下，應變速率越大所對應的壓力越大，反之亦然；且前期固結壓力與加載速率成正比。這一理論已在軟土沉降計算中得到成功應用[23]。“等速線理論”最初是針對靜力問題發展而來，參數可以通過常規的固結加載試驗獲取。考慮到土體的震陷是在動荷載條件下產生的變形，因而相關參數的獲取需要充分考慮動荷載加載速率的影響，并對其進行修正。因而，將“等速線理論”應用于預測黃土震陷特性的關鍵在于對其相關參數進行必要的修正，使其能夠準確反映動荷載對土體沉陷的影響。

本文以蘭州黃土為研究對象，進行不同加載速率條件下的壓縮試驗。獲取相關模型參數，對比分析加載速率對模型參數的影響，并提出針對動荷載的模型參數獲取方法。同時,根據不同加載頻率和震動幅值條件下的應力應變試驗結果驗證“等速線模型”的正確性，進一步分析震動荷載條件下黃土變形的影響因素及規律。

1 控制方程及數值實現

“等速線理論”將外荷載作用下土體產生的總應變分為彈性應變 (εe) 和黏塑性應變(εs)兩部分，即：

ε=εe+εs

(1)

其中，彈性應變速率為：

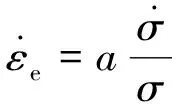
(2)

黏塑性應變速率為：

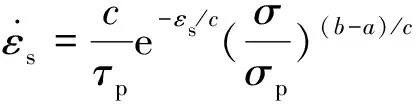
(3)

則土體的總應變速率可寫為：

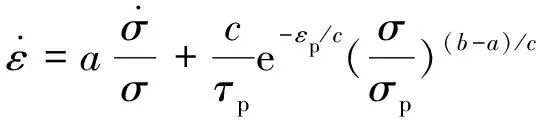
(4)

將式(4)對時間積分則可得到土體的總應變：

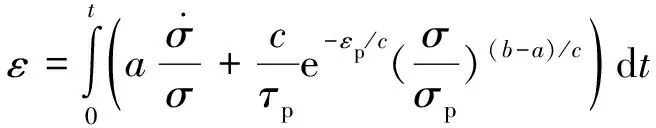
(5)

式中：a——回彈系數，為ε-lnσ壓縮曲線上彈性階 段的斜率；

b——塑性壓縮系數，為ε-lnσ壓縮曲線上塑性階段的斜率；

c——黏塑性應變速率參數，為恒定荷載條件下應變對應于時間對數的斜率；

τp——內變量參考時間，等于逐級加載試驗中每級荷載的持續時間；

σp——前期固結壓力；

σ——當前應力。

式(5)給出了土體在荷載作用下總應變的積分計算公式，但其結構形式較為復雜，很難得到嚴密的解析解，因而可以將式(4)轉化成增量形式，進而求取總應變的數值解。式(4)的增量形式可寫為：

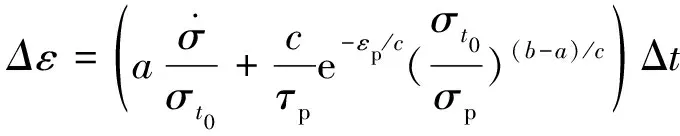
(6)

式中：σt0——t0時刻土體的應力。

則土體的總應變則可表示為：

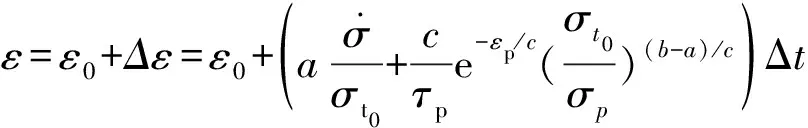
(7)

式中：ε0——t0時刻土體的總應變。

通過式(1)～(7)，本文推導了基于“等速線理論”的土體總應變的數值計算公式，下面將進一步開展不同加載速率條件下的K0壓縮試驗，并根據正弦震動荷載壓縮試驗結果探討相關參數的獲取方法，并驗證該理論在預測震動荷載條件下土體應變的正確性。

2 試驗介紹及參數獲取

本文以蘭州黃土為研究對象，其液限和塑限分別為26.7%和14.3%，級配曲線如圖1所示。試驗中所用土樣均為重塑土樣，先對土樣進行烘干、磨粉，過孔徑為2 mm的土樣篩。將過篩的土樣加蒸餾水攪拌均勻并控制含水量在9%。再將濕潤的土樣裝進內徑與高度分別61.8 mm和20 mm 的模具內壓制成型。通過控制加入土樣的質量，制備成干密度為1.60 g/cm3的土樣。為了研究不同加載速率對土樣力學參數的影響，對每組土樣進行5種不同加載速率的K0壓縮試驗，即：第一種以50 kPa/s 的加載速率將土樣荷載從0 kPa施加至1 000 kPa；其他4種加載試驗采用七級不同壓力(50，100，200，400，600，800，1 000 kPa)對土樣進行逐級加載，加載過程中采用4種不同的荷載持續時間(10，30，60，120 min)來代表不同的加載速率。另外，對相同干密度的土樣進行不同頻率和平均應力條件下的正弦震動荷載K0壓縮試驗,具體試驗安排如表1所示。

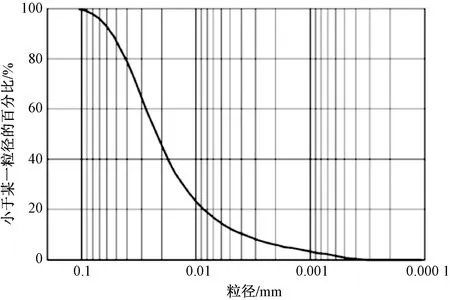
圖1 蘭州黃土顆粒級配曲線Fig.1 Grain size distribution of the Lanzhou loess

荷載頻率/Hz平均應力/kPa應力幅值/kPa0.2020025300500.022002530050

如式(1)～(7)所述，基于“等速線理論”描述土體的應力應變關系需要首先根據試驗數據獲取該理論中的5個模型參數，即：a，b，c，τp和σp。這里以每級壓力加載時長為1 h的K0加載試驗結果為例進行說明。圖2為加載時程1 h條件下得到的應力應變(ε-lnσ)曲線。圖中，應力應變曲線可分為2個階段，即：彈性階段和塑性階段。a和b分別為這2個階段應力應變曲線的斜率。根據Casagrande法，在曲線上，找出曲率最大點m，作水平線m1和m點切線m2，再作m1和m2的角分線m3，m3與塑性階段延長線交于點B，B點對應的應力值為先期固結壓力σp。內變量參考時間則為每級壓力的加載時長1 h。對于黏塑性應變速率參數c，可以通過每級壓力條件下應變與時間對數的曲線獲取(圖3)。從圖3可以發現，在各級壓力條件下，土體應變隨時間對數的變化曲線為一系列平行線，因而c取為這些平行線的斜率。根據以上相關參數的獲取方法，表2為不同加載速率(加載時長)條件下得到的相應模型參數。其中，對以50 kPa/s直接加載至1 MPa的參數由于無法通過試驗數據直接獲取參數τp和c。因而在實際計算同通過參考不同加載時長數據獲取的相應參數。通過表2可以發現，雖然參數a，b和σp均會隨著加載速率的升高而產生相應變化，但參數c的變化隨加載速率的改變并不顯著。因而，對于50 kPa/s獲取的參數中缺少的參數c可以取不同加載速率條件下c的平均值；對于τp，由于荷載是以50 kPa/s的速率進行加載，因而可以取為1 s。下面將基于這些模型參數以及震動荷載條件下的試驗結果，進一步驗證該模型在描述動力條件下土體力學行為的可靠性，并對比分析試驗和計算結果探討適用于動荷載條件的模型參數獲取方法。

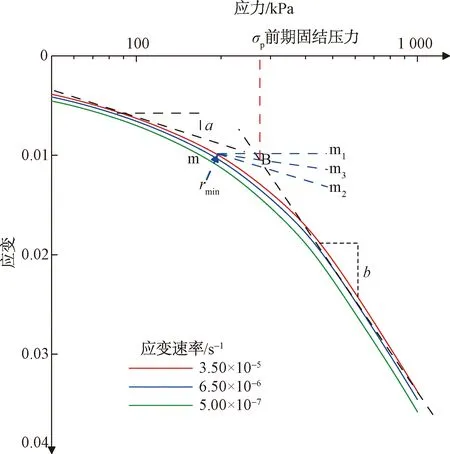
圖2 應力應變關系曲線圖(1 h加載時長)Fig.2 Stress-strain curve(1 hour loading time)

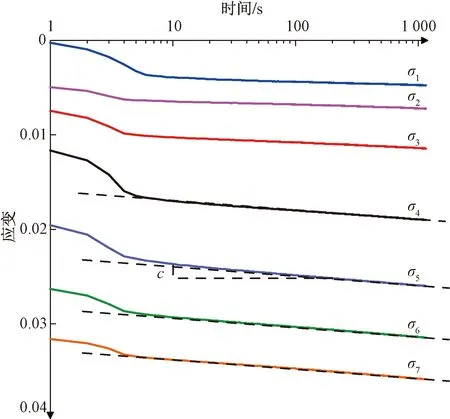
圖3 各級壓力下應變隨時間發展關系Fig.3 Variation curve of soil strain with time under different load conditions (1 hour loading time)

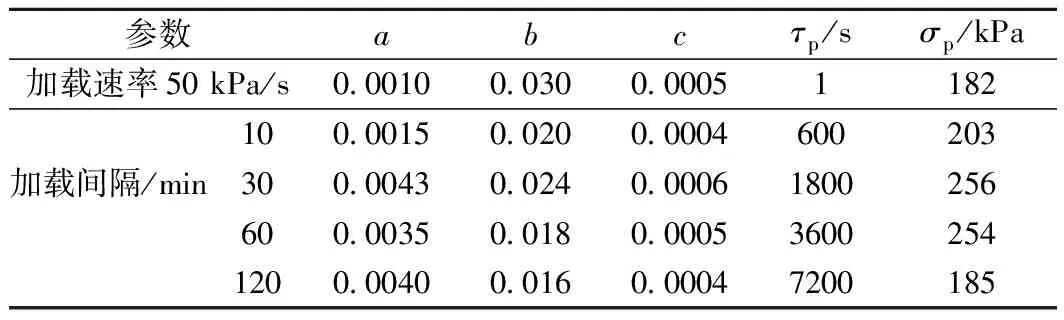
參數abcτp/sσp/kPa加載速率50 kPa/s0.00100.0300.00051182100.00150.0200.0004600203加載間隔/min300.00430.0240.00061800256600.00350.0180.000536002541200.00400.0160.00047200185

3 結果分析及理論驗證

3.1 理論驗證

圖4為不同荷載頻率、平均應力以及應力幅值條件下土體動應變隨時間發展的計算和實測結果。從圖4中可以看出，由不同時間間隔逐級加載試驗獲取參數的計算與實測結果偏差較大，而由50 kPa/s加載速率試驗數據獲取的參數的計算結果與實測結果吻合較好。這表明針對土體靜力學問題發展而來的“等速線理論”在描述土體震動荷載條件下的應力應變行為時具有較好的適用性，但其模型參數的獲取方法不同于靜力學問題。從表2可知，隨著加載速率的增大，模型參數a，b和σp的變化較為顯著，而c基本保持不變；其中受加載速率影響最大的則是內變量參考時間τp(在計算動力學問題時取值應小于靜力學取值的2～3個數量級)。這說明，隨著加載速率的升高，表征土體壓縮特性的回彈系數(a)和塑性壓縮系數(b)以及代表土體應力歷史的前期固結壓力(σp)均會受到一定的影響，且與加載速率正(或負)相關，但對模型計算準確性起關鍵作用的是內變量參考時間(τp)的量值，而代表土體恒定荷載條件下的黏塑性應變速率參數(c)受加載速率的影響較小。因而，基于“等速線理論”描述動荷載條件下土體的力學行為，其模型參數a，b，σp以及τp應根據具體動荷載的加載速率獲取相應參數，而黏塑性應變速率參數c則可參照靜力加載試驗獲取。以上內容驗證了“等速線理論”在預測土體動荷載作用下描述其應力應變關系的適用性，并結合不同加載速率條件下獲取的模型參數探討了相應的參數獲取方法，下面將進一步基于“等速線理論”探討各模型參數對土體動荷載的影響規律，進而分析一維狀態下土體對動荷載的響應。

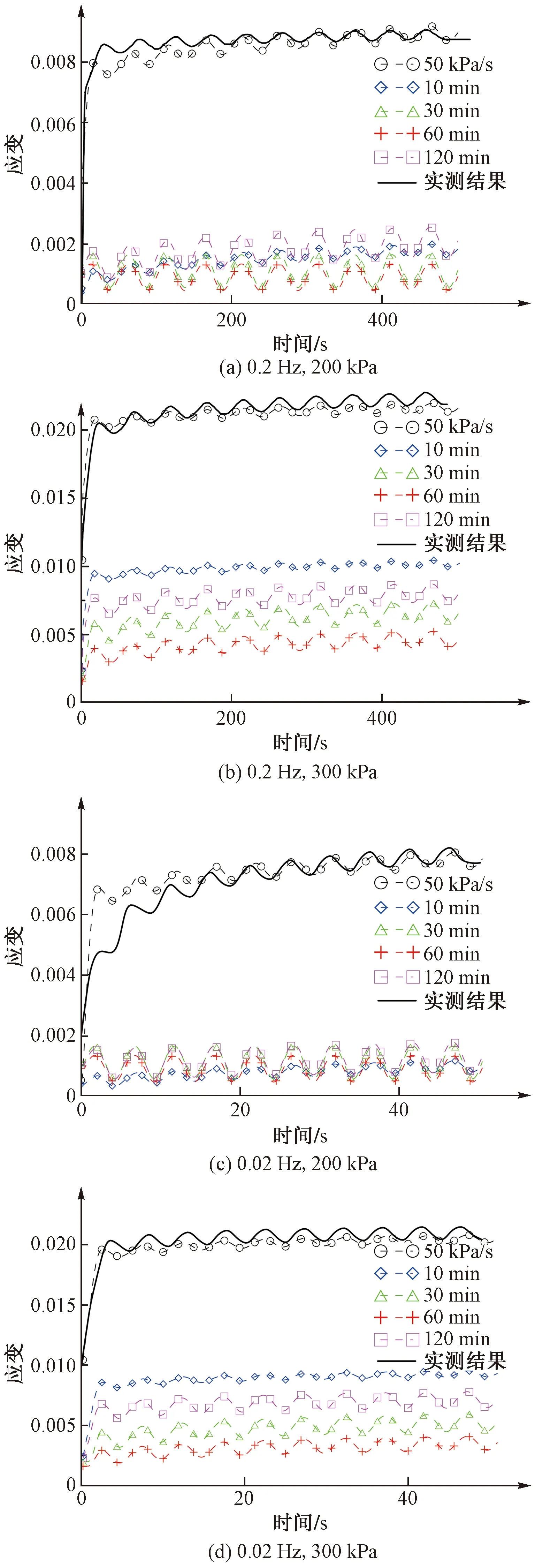
圖4 不同荷載頻率、平均應力以及應力幅值條件下土體動應變時程曲線Fig.4 Duration curves of dynamic strain under different load frequency,average stresses and stress amplitudes

3.2 動荷載響應分析

回顧式(7)可以發現，土體在動荷載作用下產生應變包括兩個部分：即，彈性和塑性應變。其中回彈系數c決定了動荷載作用下彈性應變，而參數(b-a)/c和應力比(震動荷載平均應力與前期固結壓力之比)決定了動荷載作用下土體中發生的塑性應變。為了進一步分析不同模型參數條件下土體的動力學響應，圖5～圖7分別給出了不同回彈系數a，(b-a)/c以及應力比(震動荷載平均應力與前期固結壓力之比)條件下動應變的計算結果。從圖5可以看出，在其他參數保持不變的情況下，土體的動應變幅值與回彈系數正相關；而在土體的回彈系數c保持恒定的條件下，土體動應變初始階段發生的塑性變形則正比于(b-a)/c。同時，(b-a)/c的改變對動應變幅值的影響并不顯著(圖6)。同樣土體初始階段發生的塑性應變也正比于應力比(圖7)。通過以上分析表明，(b-a)/c和應力比決定了動荷載初期作用下發生在土體中的塑性應變(“殘余應變”)。這說明，動荷載作用下發生在土體中的“殘余應變”是土體塑性壓縮特性以及受力歷史共同作用的結果。因而，在評價土體動荷載作用下的“殘余應變”時，應綜合考慮土體參數和應力水平的影響，而土體動應變的幅值則主要取決于土體的回彈系數。

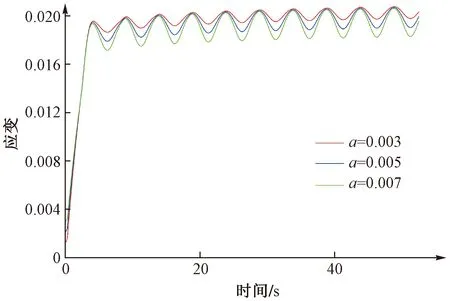
圖5 彈性壓縮系數a對動應變的影響Fig.5 Effect of elastic compression coefficient (a) on the dynamic strain

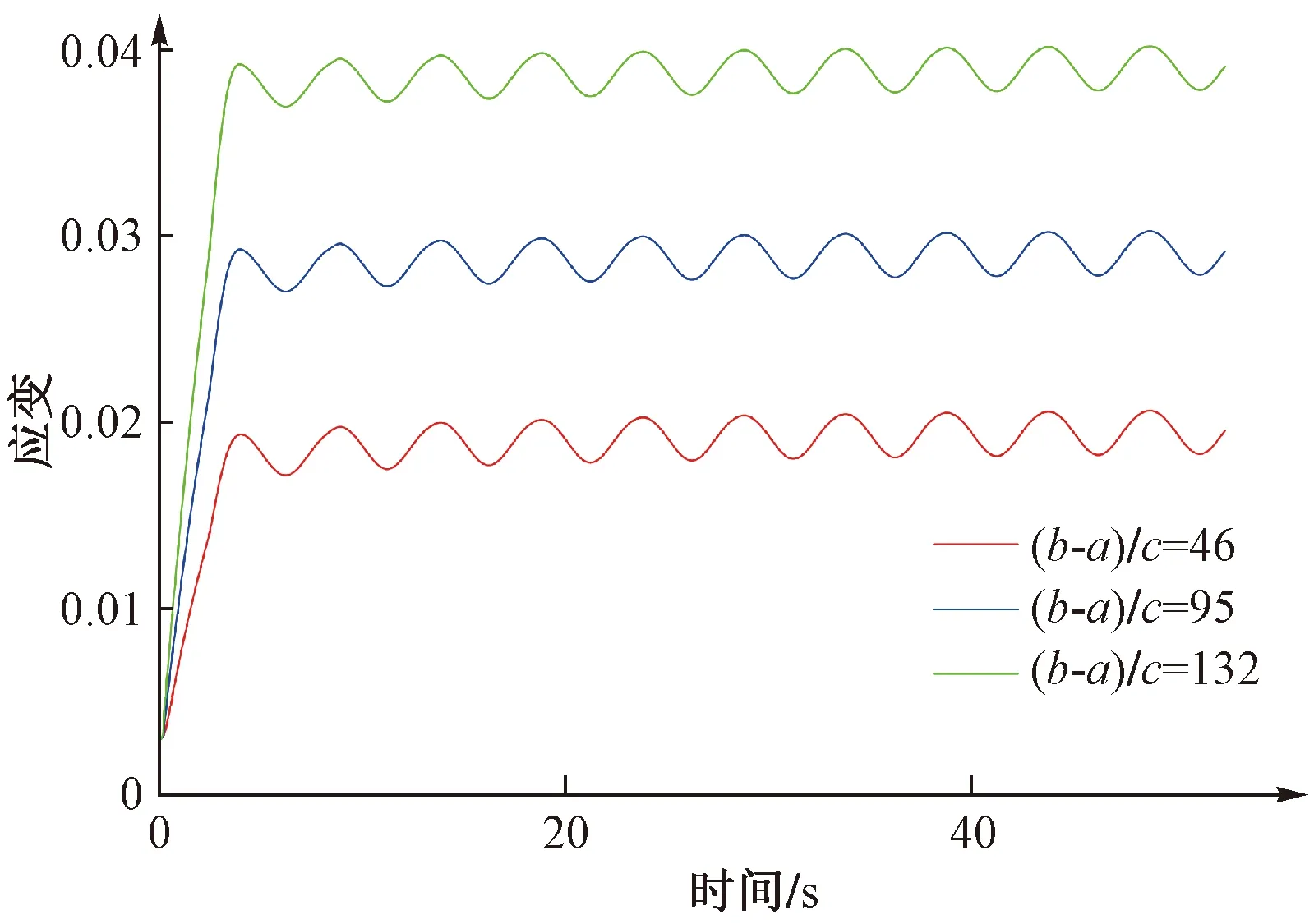
圖6 ((b-a)/c對動應變的影響Fig.6 Effect of (b-a)/c on the dynamic strain

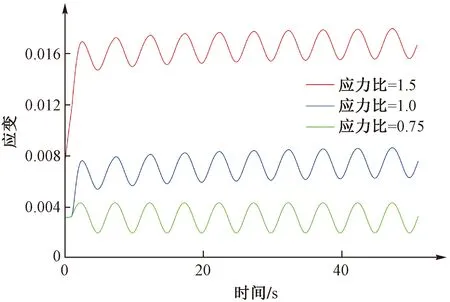
圖7 應力比對動應變的影響Fig.7 Effect of stress ratio on the dynamic strain

4 結論

(1)隨著加載速率的升高，回彈系數(a)、塑性壓縮系數(b)、前期固結壓力(σp)和內變量參考時間(τp)均會產生顯著變化，而黏塑性應變速率參數(c)則受加載速率影響較小。因而，在動力學計算中應充分考慮加載速率對a，b，σp和τp的影響。

(2)震動荷載作用下，對比不同加載速率條件下得到的模型參數的計算結果和實測結果顯示，針對靜力學問題發展而來的“等速線模型”也能夠應用于描述震動荷載條件下土體的應力應變發展規律。其中，對預測精度影響最為顯著的是模型參數τp；參數a，b和σp的影響次之。在計算動力學問題時，τp的量值較靜力條件下獲取的參數要小2～3個數量級，這是使用該模型計算動力學問題時與靜力問題的最大不同。

(3)基于“等速線模型”的動力學響應分析表明，土體在震動荷載作用下，其動應變幅值與回彈系數正相關而(b-a)/c和應力比正比于動荷載初期作用下發生的塑性應變(“殘余應變”)。因而，在評價土體動荷載作用下的“殘余應變”時，應綜合考慮各力學參數和應力狀態的影響。