基于matlab的CPU復位機理研究

李隊員，朱廣

(1.安徽交通職業技術學院 城市軌道交通與信息工程系，安徽 合肥 230051；2.安徽建筑大學 機械與電氣工程學院，安徽 合肥 230601)

0 引言

復位是CPU一種初始化操作[1]，復位的目的是使邏輯電路按照程序設計者的設計“按部就班”確定地工作。復位電路設計是CPU控制系統設計的基礎和一項基本技能[2]。但公開資料很少有對復位電路的復位原理進行推導和定量求解，一線工程師在進行復位電路的設計時，對電阻和電容值的選擇也多依據經驗或粗略估算，從而造成CPU的復位時間不可知或復位不同步，給工程實踐帶來不確定性。

1 復位電路

本文以常用的性價比較高的宏晶科技的STC89C52的高電平復位電路為研究對象。分析阻容復位電路電阻和電容的大小對復位時間長短的影響，并研究其復位機理。

對于STC89C52這種高電平復位的CMOS型單片機來說，通常在芯片內部的RST管腳處接有一個下拉(PullDown)電阻，目的是將狀態不確定的RST管腳通過一個電阻箝位至低電平，以防止該管腳因懸空而出現不確定的狀態，繼而導致系統出現不期望的結果。

通過查芯片手冊可知RST管腳下拉電阻最小為40KΩ，最大為225KΩ，漏電流為10μA，由于該電阻較大，造成復位時間過長，通常在芯片外部會并聯一個10 K下拉電阻，由于有下拉電阻的存在，在無外界作用下，RST管腳為低電平，即工作電平為低電平。

但單片機在啟動時需要復位，以使CPU及系統各部件處于確定的初始狀態，并從初態開始工作。

STC89C52復位需要在RST管腳施加高電平且持續時間大于2個機器周期。從芯片手冊查得VⅠH1 為 0.7VCC～VCC+0.5，若 VCC 取 5 V，則作用在RST管腳上的復位電平為3.5 V～5.5 V。一個機器周期等于12個晶振周期，如果晶振選12 MHz，則晶振周期為一個機器周期為12*T=1μs，即復位時間必須大于 2μs。

為了穩定可靠復位，復位時間通常要大于2個機器周期，一般選遠大于2個機器周期的10 ms作為復位時間的分界點，大于10 ms則認為能夠可靠復位，宏晶科技推薦的阻容復位的電容為10 uF，電阻為10 K[3]也是以此為依據的。

常見的復位電路如圖1所示的兩種形式，左邊為低電平復位電路，右邊為高電平復位電路，具體選擇哪種需要參照CPU的數據手冊。

2 瞬態模型

當電路中電壓、電流等為某一穩定值或某一穩定時間函數，稱之為電路的穩定狀態，簡稱穩態。當電路從原來的穩態變換到新的穩態，需要經歷一定的時間，變換過程中，u、i都處于瞬間的不穩定狀態，所以過渡過程又稱為電路的瞬態過程，電容兩端電壓的瞬態過程如圖2所示。

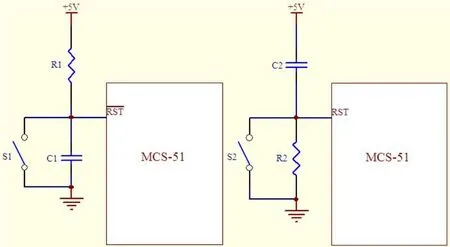
圖1 單片機復位電路原理圖

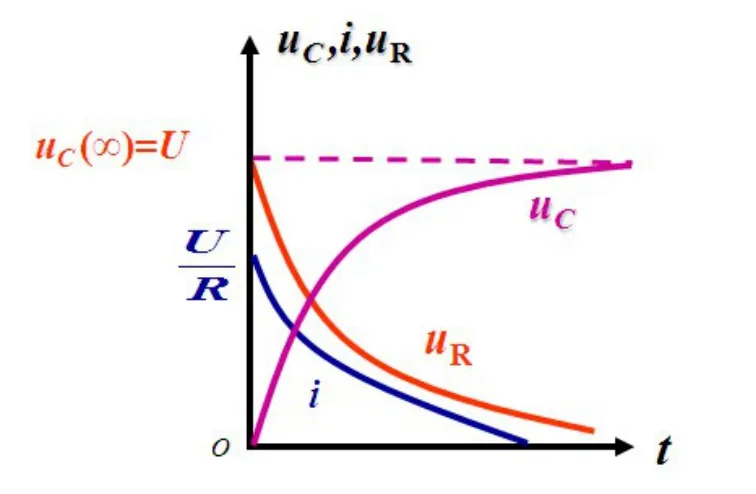
圖2 瞬態過程

CPU正是利用上電的瞬態過程來進行復位，在達到新的穩態后，復位過程結束，進入工作狀態。

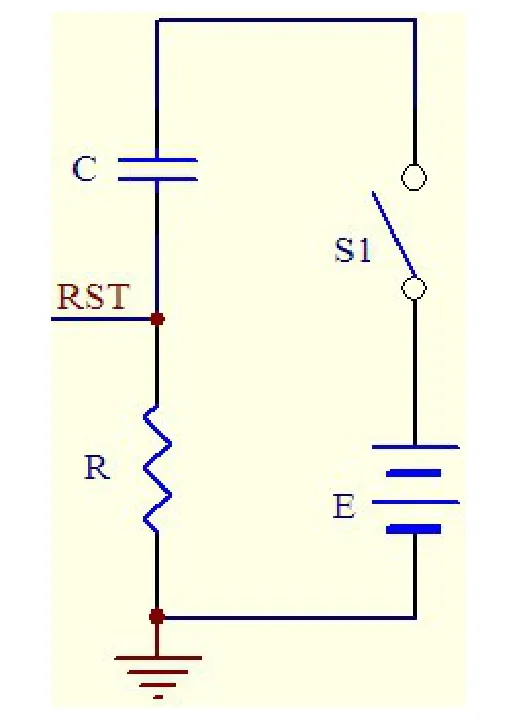
圖3 簡化模型

CPU上電高電平復位的簡化模型如圖3所示，低電平復位電路類似，通過開關S1的閉合來模擬上電復位。當開關S1閉合，電源通過閉合回路給電容充電，回路中有充電電流流過，在電阻R上產生瞬態電壓即URST作用于CPU的復位管腳，當瞬態電壓幅值在3.5 V以上即數字電路的高電平，且持續時間超過10 ms時，電路處于復位狀態。此高電平信號隨著VCC對電容的充電而逐漸回落，最終被下拉電阻鉗位至工作電平，上電復位過程結束。

2.1 開關S1閉合前初始狀態

t=0時,UC=0;UR=0;

2.2 開關S1閉合后(開關閉合無抖動)

設電路中的電流為i(t)，電容器極板上的電荷量為q(t)，兩極板間的電壓為Uc，由電學可知:

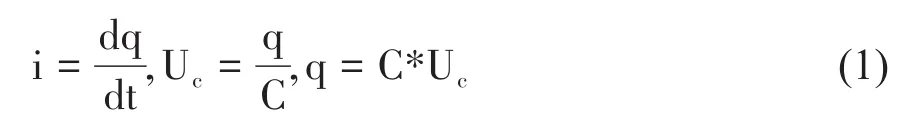
根據回路電壓定律得[4]:

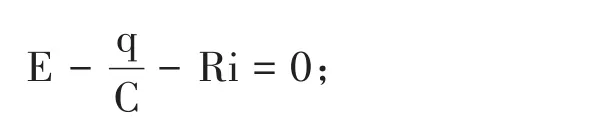
即

將公式(1)帶入(2)得:

對于給定的電阻、電容，二者乘積一定，所以，

令 τ=RC，則(3)式為

上式對應的齊次方程為:

采用所謂的常數變易法來求解(3)式的非齊次線性方程的通解[5]為:

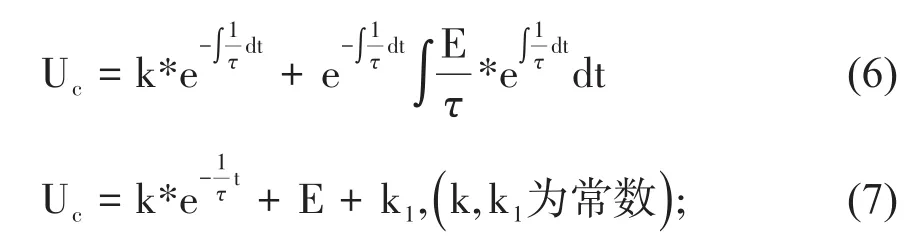
將初始條件t=0,Uc=0(電容電壓不能突變)以及由電學可知t=∞,Uc=E帶入(7)解得:

在一般的單片機電路中，取E=5 V，得出:

則

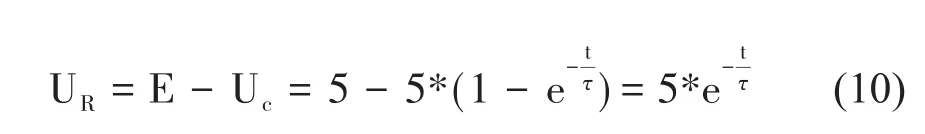
在不考慮單片機RST管腳吸收電流的情況下，低電平復位電壓為Uc，高電平復位電平為UR。

3 Matlab求解驗證

圖2瞬態過程呈現了電路從一個穩態到另一個穩態變化過程中電容電阻兩端電壓變化的趨勢，具體到某一時刻對應的電壓值則難以確定，因此圖2屬于定性描述。

為了獲得定量分析值，需要借助matlab來對公式(10)電阻的電壓值 UR作圖，復位電平取0.7*VCC=3.5 V，即RST管腳上電平大于3.5 V時，CPU處于復位狀態。

求復位電平3.5 V與公式(10)所作圖形交點的時間t的值，該時間t即為高電平復位時間。

用matlab[6]編寫如下程序求解:num2str(t3*1000)，'ms'])；

title('高電平復位電壓與時間圖')；

xlabel('時間t取值范圍是0-0.2，單位是s')；

ylabel('電壓 U，單位是 V')；

legend(['τ1=RC='，num2str(a)]，['τ2=RC='，num2str(b)]， ['τ3=RC='，num2str(c)])；

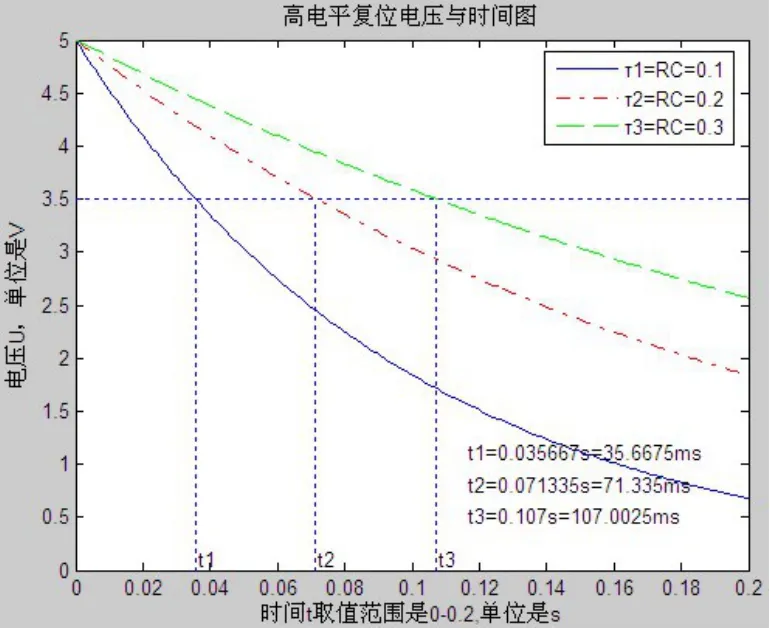
圖3 復位時間

從圖3可以看出，當τ=τ1=RC=0.1(宏晶科技推薦值)時，復位時間為 t1=0.356675 s=35.6675 ms，大于10 ms，滿足復位的時間要求。

隨著τ=RC的增大，復位時間變長，即t1＜t2＜t3。

4 結論

對CPU復位的瞬態過程進行了闡述，研究了充電過程中作用于CPU管腳的復位機理并建立微分方程，利用復位電路的初始條件和新的穩態條件求解，得出復位電路的復位電壓與時間常數τ之間的函數關系式，采用matlab對函數作圖并求解，形象化地呈現了不同時間常數τ=RC與CPU復位時間的關系，提供了一種定量求解的方法和途徑，對廣大工程技術人員的復位電路設計具有一定的參考價值。