一種基于傅立葉變換的時延測量方法及應用*

楊 麗

（上海諾基亞貝爾股份有限公司，江蘇 南京 210037）

0 引 言

測量系統的信號時延在工程應用上有著非常重要的作用。在無線通信領域，對信號時延測量的精度要求日益提高。對于多個系統，除了測量信號時延，有時還需要根據測量的結果對信號進行時延補償，使多個系統的信號時延相同。所以，對系統時延的精確補償也非常重要。

1 常用時延測量方法

相關法和群時延法是目前被廣泛應用于系統信號時延測量的方法。

工程應用中，相關法是最基本且應用最廣泛的方法，適用于具有較好相關性的信號，如偽隨機序列、線性調頻信號以及LTE信號都具有較高峰值旁瓣比。相關法利用同時采樣的信號數據對數據進行相關處理，搜索相關結果的峰值位置，與信號的長度進行比較計算，得到信號間的相對時延。

以線性調頻信號為例，圖1是時延系統的輸入和輸出信號，信號1是輸入信號，信號2是輸出信號。從圖1可以看出，信號2相對信號1有一定的時延。二者相關結果如圖2所示，最大值所在的位置50即表示信號2相對信號1的時延是50個采樣點，根據每個采樣點對應的時間可以計算出時延。

圖1 系統輸入和輸出信號

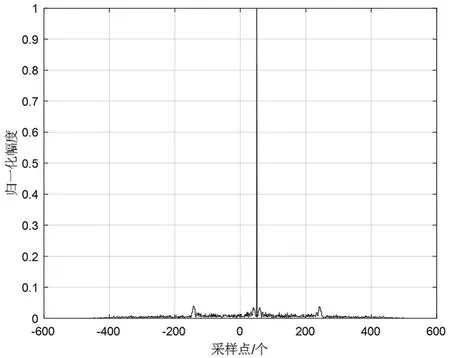
圖2 相關結果

相關法測量時延的精度與采樣點對應的時間間隔有關，通過插值處理可以提高測量精度，但會增加計算量。對于相關性差的信號形式，相關法的測量結果誤差增大甚至失效。

群時延法不受信號形式約束，是利用信號的相位變化得到時延，群時延即相位變化的梯度，定義為：

其中為相位（單位：rad），ω為角頻率（單位：rad/s）。

2 基于傅立葉變換的群時延計算方法

群時延法應用范圍廣泛。基于該方法得到了一些更適于工程應用的時延測量方法。文獻[1]提出了一種通過濾波器的傅立葉變換計算該濾波器群時延的方法。濾波器的時域系數為h(n)，階數為N，n=0,1,2…,N-1。h(n)的傅立葉變換為H(ω)：

其中M(ω)為濾波器的幅頻響應，φ(ω)為濾波器的相頻響應。

根據式（2）得到計算群時延的公式（具體推導過程參見文獻[1]）：

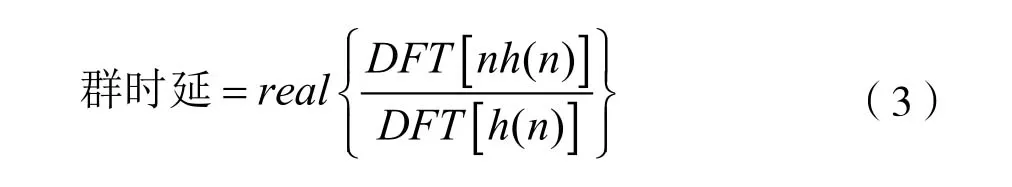
群時延的單位為h(n)信號的采樣時間間隔。

以一個11階的sinc函數作為濾波器系數為例，h(n)=[0.0189,-0.0190,0.0191,-0.0192,0.0192,0.9619,0.0192,-0.0192,0.0191,-0.0190,0.0189]，如圖3所示。根據式（3）計算得到的群時延如圖4所示。

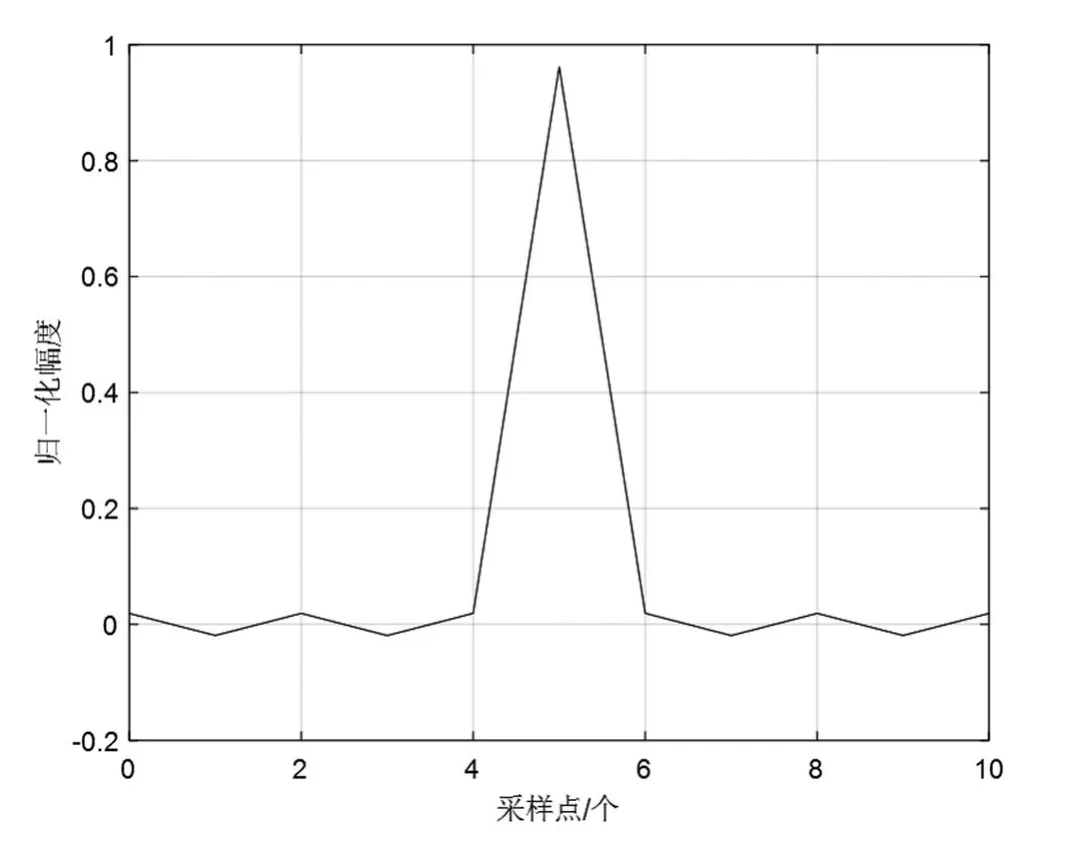
圖3 濾波器系數h(n)

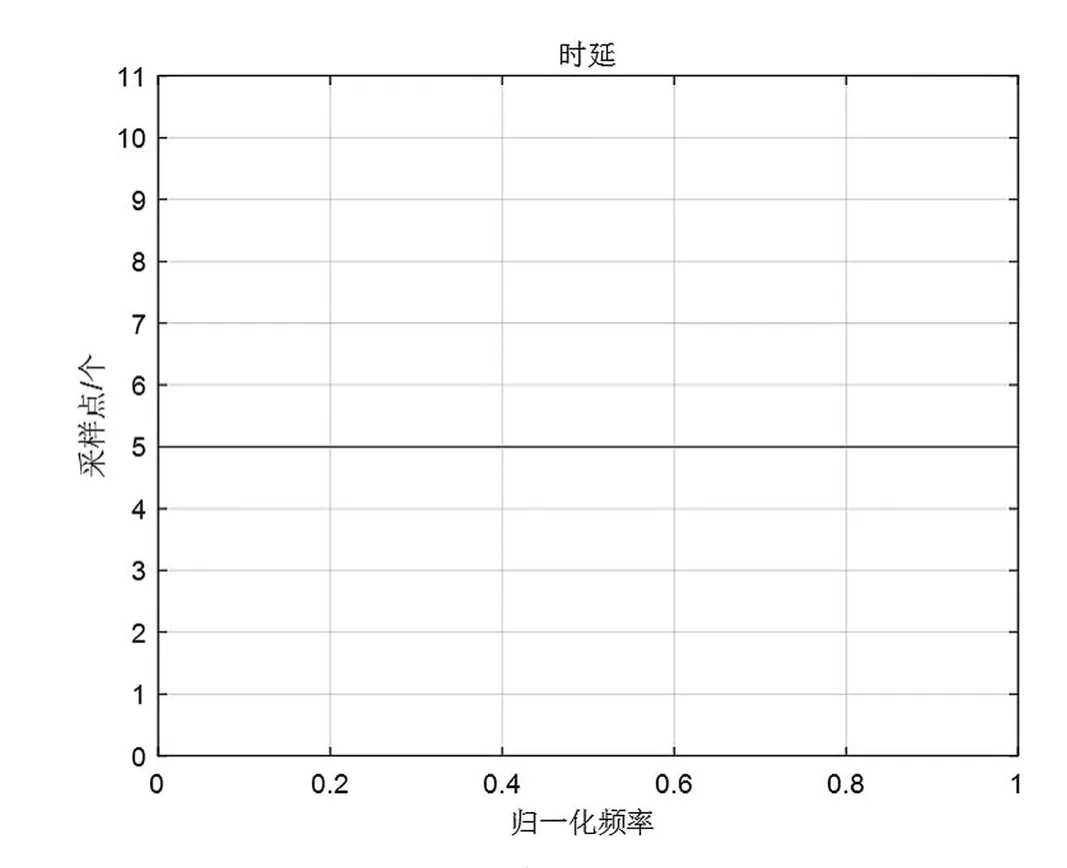
圖4 濾波器的群時延

從圖4可以看出，圖3所示的濾波器系數在各個頻率的時延都為5個采樣點，根據采樣點對應的時間間隔可以計算濾波器的群時延。

3 基于傅立葉變換的群時延計算方法在通信系統中的應用

文獻[1]提出的方法用于計算濾波器的時延。當使用特定的信號作為系統的輸入信號，根據系統的輸出數據，利用文獻[1]的方法可以得到系統的處理延時。圖5是利用文獻[1]的方法測量系統時延的框圖。

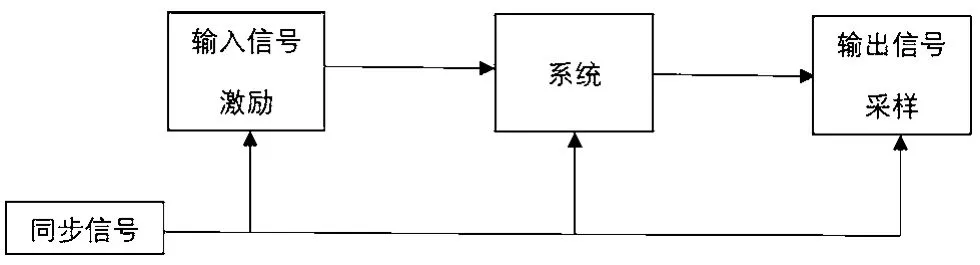
圖5 測量系統時延方法

測量系統需要輸入信號、系統處理、輸出信號采樣之間有共同的同步信號作為觸發信號，同步信號可以是同一信號或具有固定時延的信號。同步信號的周期間隔需要大于系統的時延時間。輸入信號采用狄拉克函數[2]。圖6（a）和圖6（b）是同步信號和輸入信號，輸入信號與同步信號之間的時延為0。假設系統實現一個如圖3所示的濾波器的處理，則以同步信號為觸發采樣的輸出信號如圖7（a）和圖7（b）所示。圖6（c）和圖7（c）是分別利用文獻[1]的方法計算的得到的群時延結果，輸出信號相對輸入信號的時延為兩者之差，即系統的群時延，計算結果同樣為5個采樣點，與圖4的結果一致。所以，當不知道系統的具體處理過程時，根據系統的輸入信號和輸出信號同樣可以計算出系統的時延。為了減少帶外噪聲的影響，通常取有限帶寬內的多個頻率時延的平均值作為系統的時延。

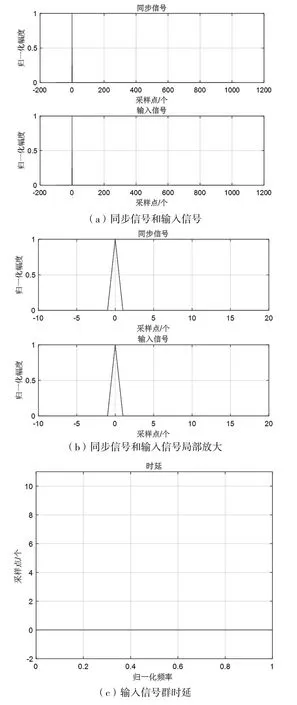
圖6 系統輸入信號時延測量

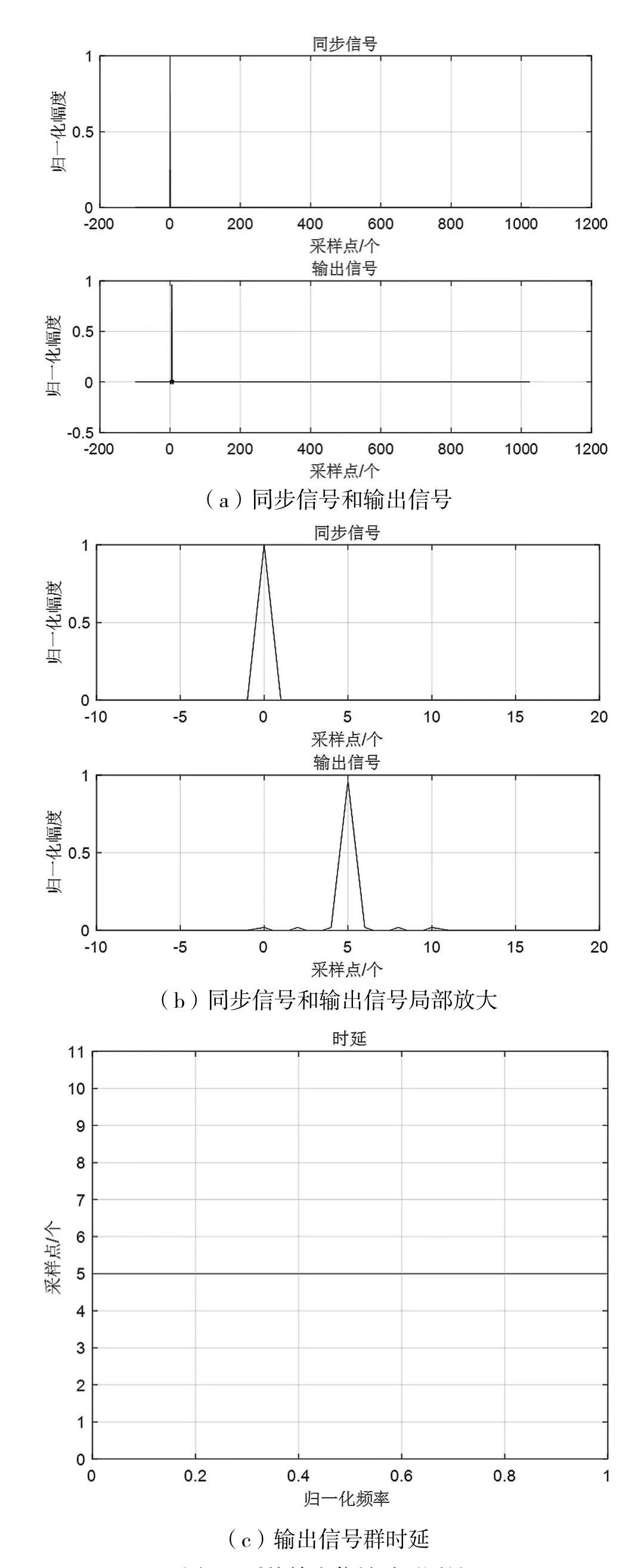
圖7 系統輸出信號時延測量

通過上面的方法計算得到了系統的時延，有時還需要根據時延的結果對信號進行時延補償，使多個信號或系統之間的時延相同。從圖3和圖4可以看到，利用辛格函數得到的濾波器系數，它的峰值所在的位置決定了該濾波器的時延，因此可以利用辛格函數產生時延濾波器系數。當時延值較大時，濾波器的階數較長，實現時占用資源較多。因此，可以把時延拆分成3部分，即：

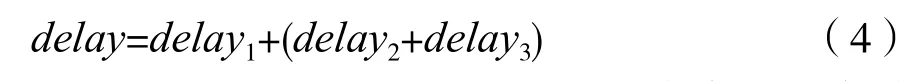
較大的整數時延delay1可以通過寄存器或存儲器處理，較小的整數時延delay2和小數時延delay3通過辛格函數產生的濾波器實現。以圖3的11階系數為例，它實現了5個整數采樣點的時延。如果delay2=5、delay3=0.5，即實現5.5個采樣點的時延，則新的濾波器系數如圖8所示。如果delay2=5、delay3=0.8，即實現5.8個采樣點的時延，則新的濾波器系數如圖9所示。

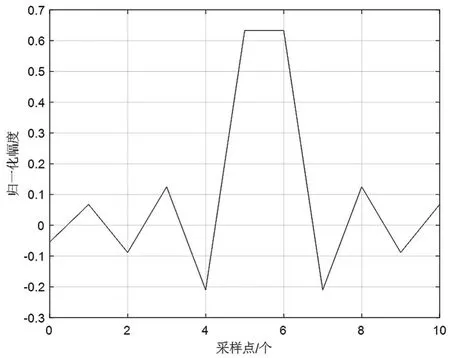
圖8 濾波器系數h(n)，delay=5.5

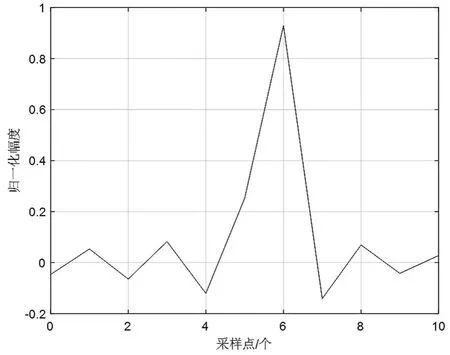
圖9 濾波器系數h(n)，delay=5.8

在通信系統中，為了保證信號不失真的前提下提高功放效率，通常會采用預失真處理[3]。預失真處理要求前向數據和反饋數據在時間上對齊，本文提出的時延測量和補償方法可以用于預失真前的數據對齊。

4 結 語

本文分析的相關法和群時延法適用于不同的應用場景，是目前工程上應用較為廣泛的方法。基于傅里葉變換測量時延的方法，方便系統實時測量時延值，該方法測量的時延結果包含系統的整數和小數個采樣時間間隔的時延，測量精度高。結合辛格函數設計的濾波器對測量的時延進行延時處理，可以用于不同信號或系統的時延對齊處理，易于工程實現。