基于隨機森林強化學習的干擾智能決策方法研究*

裴緒芳，陳學強，呂麗剛，張雙義，劉松儀，汪西明

（1.中國人民解放軍陸軍工程大學 通信工程學院，江蘇 南京 210000；2.中央軍委訓練管理部信息中心，北京 100000）

0 引 言

電磁空間是現代戰爭作戰概念和技術的重要拓展，作為未來戰爭體系的物質基礎，電磁頻譜的爭奪和反爭奪將成為戰爭制勝的關鍵[1-2]。近年來，人工智能技術的迅猛發展為電子對抗領域開辟了新的思路[3-6]。為提高惡劣電磁環境下的通信對抗能力，急需研究應對敵方干擾攻擊的抗干擾技術，以保障己方在惡劣電磁環境中的正常通信。同時，利用干擾攻擊影響并破壞敵方的無線通信，也是提升通信對抗能力不可或缺的一部分。在電磁頻譜對抗環境下，為了對敵方通信實施有效干擾，引入了智能干擾的概念。

傳統的干擾模式主要有定點干擾、掃頻干擾、梳狀干擾和跟蹤干擾等。然而，由于這幾類干擾模式相對固定且模式單一，通信用戶可以輕易尋找到干擾的變化規律而成功躲避干擾。若要對敵方通信實現精準有效干擾，必須提高干擾算法的智能性。針對現有干擾技術存在的缺點與不足，美國國防高級研究局（DARPA）開展了行為學習自適應電子戰（BLADE）、自適應雷達對抗（ARC）和極端射頻條件下的通信等研究項目，引入自主學習機制以實現穩健通信，獲取戰場環境的電磁權。相比于傳統的干擾技術，智能干擾所面臨的挑戰主要有：（1）敵方通信用戶通信策略時刻變化，目標識別獲取困難，干擾方需要準確獲取目標特征，快速生成最佳干擾；（2）干擾方必須具備在線持續學習能力，根據環境的動態變化不斷產生后續干擾策略。

近年來，很多學者在智能干擾方面展開了研究[7-10]。文獻[7]研究了多天線MIMO無線通信鏈路的智能干擾攻擊問題，提出了一種最優干擾信號設計方案，當收發機采用抗干擾機制時，可以最大限度地干擾MIMO傳輸。文獻[8]研究了干擾偽隨機碼相位調制引信，提出了一種基于多時延智能欺騙的新型干擾方法，并通過仿真驗證了智能干擾算法的有效性。文獻[9]提出了一種多臂式結構的干擾策略，能夠自適應調整功率，有效地干擾敵方用戶通信，且證明了算法可以收斂到最優干擾策略。文獻[10]從強化學習的角度出發，設計了一種基于強化學習的智能干擾算法，干擾機通過自主學習，可以實現對敵方通信用戶進行跟蹤干擾的目的。

受文獻[10]的啟發，本文提出了一種基于隨機森林強化學習的智能干擾算法。干擾方可以通過學習用戶的信道切換規律，不斷優化干擾策略。與文獻[10]不同之處在于：（1）在系統模型層面，文獻[10]只考慮干擾單個通信用戶，而本文同時干擾兩個通信用戶；（2）在算法設計層面，文獻[10]使用經典Q學習算法，而本文提出了一種基于隨機森林強化學習的智能干擾算法；（3）本文所提算法重新定義了系統的效用回報為干擾的占空比，算法收斂速度更快。

文章章節設置如下：第1節給出系統模型，并將干擾策略的決策過程建模為一個MDP過程；第2節針對建立的問題模型，提出了一種基于隨機森林強化學習的智能干擾算法；第3節給出了仿真結果，并分析了算法性能；最后，進行總結。

1 系統模型及問題建模

1.1 系統模型

本文考慮無線通信網絡中存在1個干擾機、1個認知引擎和2個用戶，系統模型如圖1所示。系統的全頻段頻譜被劃分為M個帶寬相等的信道，信道集表示為每個信道帶寬為W。通信用戶雙方采用掃頻、梳狀以及隨機等信道切換策略進行通信，干擾方通過認知引擎獲得信道狀態信息，并根據獲得的信道狀態信息執行強化學習算法來學習用戶的信道切換規律，以不斷優化自身的干擾策略。假設每個用戶在每時隙只選擇一個信道進行通信，干擾方同時干擾兩個信道。

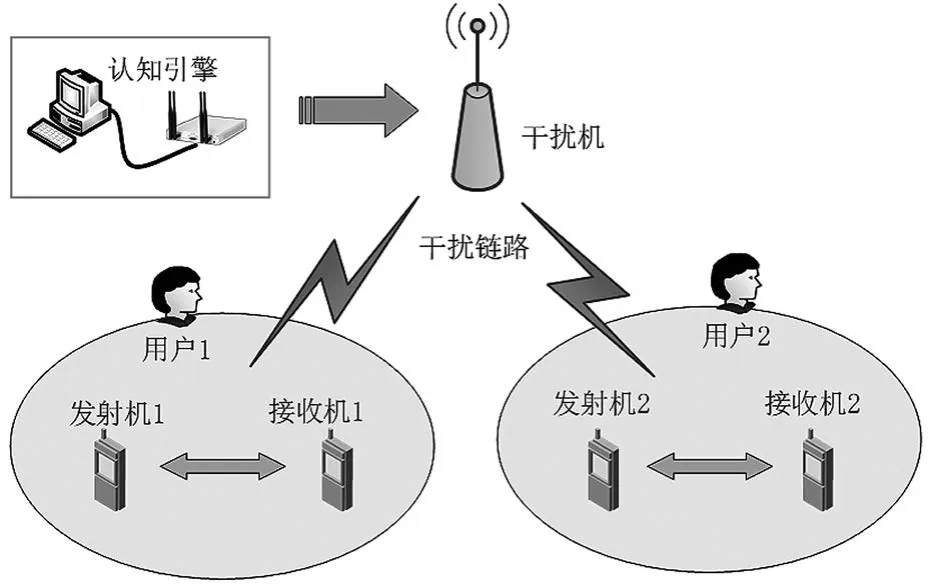
圖1 系統模型

1.2 問題建模

考慮到用戶通信信道時刻動態變化，干擾方需要探索用戶的通信規律，以對其實施有效干擾。假設系統中存在M個可用信道，為了使描述更直觀，以M=7為例進行舉例說明。假設用戶1以掃頻方式通信，用戶2以固定序列跳頻方式通信，其用戶通信信道切換示意圖如圖2所示。

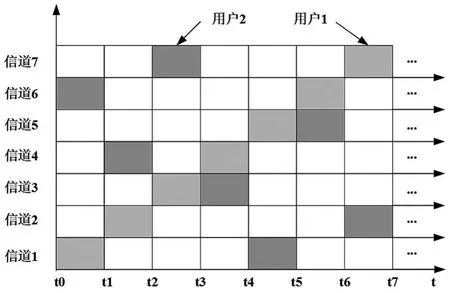
圖2 用戶通信信道切換

針對以上提出的問題，本文將干擾信道選擇問題建模為MDP過程。MDP一般用一個4元組表示，即，其中S代表狀態空間，A代表動作空間，P代表狀態轉移概率，R代表效用回報。具體定義如下。

設置狀態空間s：在n時隙時，干擾方的狀態可 表 示 為sn=(cu1,cu2)，cu1,cu2∈ {1,2,…,M}， 其 中cu1、cu2通過認知引擎的頻譜感知獲得，分別代表當前用戶1和用戶2的通信信道，因此狀態空間的大小為

設置動作空間A：在n時隙時，干擾方會選擇兩個信道進行干擾，干擾的動作可表示為an=(cj1,cj2)，cj1,cj2∈ {1,2,…,M}，cj1、cj2分 別 表 示 干擾方下一時刻選擇干擾的信道，因此動作空間的大小為

設置狀態轉移概率矩陣P：在n時隙時，表示干擾方從當前狀態sn選擇動作an到達下一時隙狀態sn+1狀態的概率。

設置干擾效用R：干擾的目標是探索最優的干擾信道選擇策略使得累計成功干擾概率最大。n時隙時，在當前狀態sn下，干擾選擇動作an，此時獲得的回報值為rn。本文中定義的rn為n時隙干擾方的占空比，即用戶單個時隙內成功干擾到用戶通信所占的比例，具體可表示為：

其中Toverlap為n時隙內用戶通信被干擾的時長，Tuser為用戶通信時隙長度。

本文中，系統的優化目標為尋找到最優的干擾策略π，最大化系統累積成功干擾概率，即：

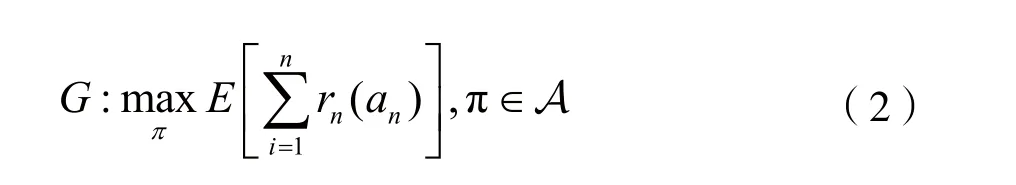
根據對動態環境下干擾信道決策問題的分析，將其建模為一個MDP。對于這種未知環境下的決策問題，通常采用強化學習（RL）[3]給予解決。近年來，Q學習作為一種最典型的強化學習方法得到了廣泛應用。與文獻[10]不同，由于本文的系統模型狀態空間較大，傳統的Q學習算法無法解決由維數增長帶來的狀態空間巨大的問題，因此本文提出了一種基于隨機森林強化學習的智能干擾算法。

2 基于隨機森林強化學習的智能干擾算法

Q學習是一種無模型的在線學習算法，無需知道環境的先驗知識，直接通過與環境不斷交互獲得最優的策略[3]。在執行Q學習算法的過程中，智能體會維護一張Q值表，用于評估不同狀態下對應各個動作的優劣程度。Q學習的基本原理如圖3所示。

圖3 Q學習基本原理

在執行算法的初始時刻，Q值表為全零矩陣，智能體會根據當前狀態sn做出一個動作an，并獲得相應的回報rn，同時更新Q值表。隨著智能體不斷地與環境進行交互，Q值表趨于穩定，策略逐漸收斂于最優。

為了使系統長期累積回報最大化，需要將單步回報值進行累加求和從而得到長遠回報。對于這種長期任務下的回報值計算，需引入折扣因子γ。為評價在給定狀態下采取某個策略好壞，一般通過值函數來反映。因此，在某一策略π下獲得的γ折扣長遠累積回報可表示為[11]：

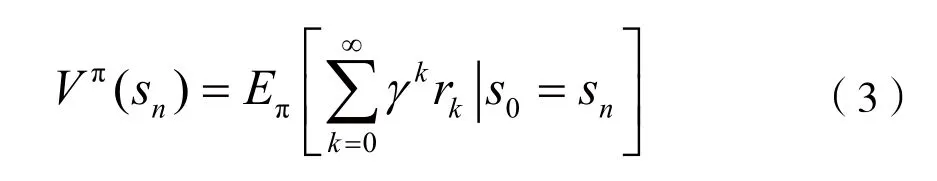
智能體在狀態sn下采取動作an獲得的Q值可表示為：

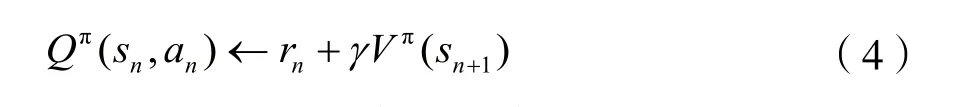
目標是找到最優策略能夠獲得最大化折扣回報，根據Bellman方程最優策略下所對應值函數V*(sn)可定義為[11]：

同理可得，對于Q*(sn)函數的Bellman最優方程可定義為：

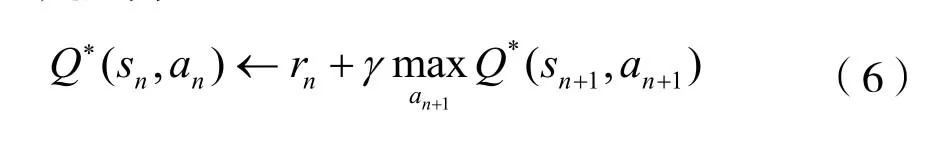
在本文所提的系統模型中，定義在sn狀態下選擇動作an，同時獲得一個回報值rn，然后更新相應的Q值。由于本文信道狀態數較多，所以采用了并行多步更新Q值的方式，即同時對每個狀態-動作對的Q值進行更新。Q學習算法的更新公式為：

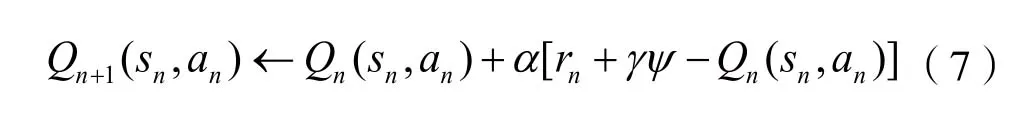
其中α表示學習速率，具體為α=1/(1+Ta(n))，Ta(n)是干擾的決策動作an在過去n個時隙中執行的次數。γ（0<γ≤1）表示折扣因子，ψ為干擾方在sn+1狀態下所有可選策略對應的最大Q值，具體表示為：

在Q學習算法執行過程中，若干擾方每一步都根據當前Q值選擇最優策略，即最大Q值對應的動作，很容易陷入局部最優而無法去探索更多的策略。與文獻[10]不同的是，本文的決策空間較大，若使用標準的Q學習，會導致算法收斂速度較慢甚至無法收斂的情況。因此，本文提出了一種基于隨機森林強化學習的智能干擾算法，即在策略選擇過程中，通過增加一個附加值來探索最優策略[5]。它可以平衡在策略選擇過程中探索與利用的關系，并且可以大大提高算法的收斂速度。策略更新公式為：

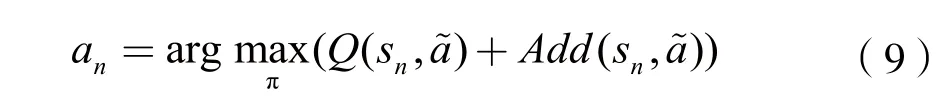
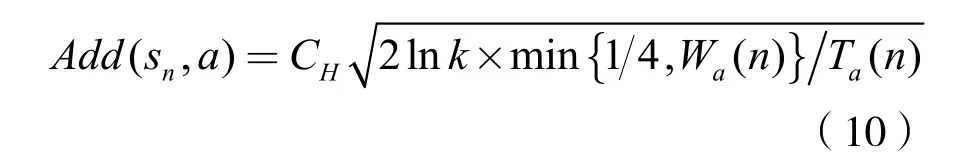
其中CH是預先設定大于零的常數，Wa(n)為偏差因子，具體表示為：

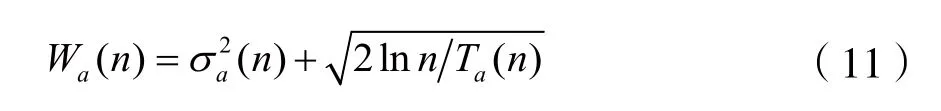
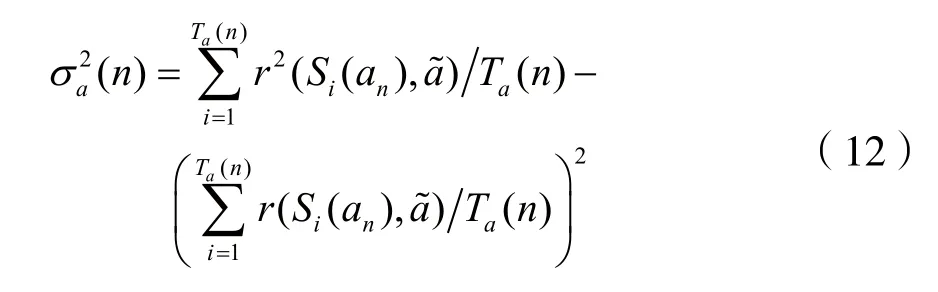
其中Si(an)為選擇決策動作an的第i個狀態，rn為當前狀態sn下的即時回報值。干擾在選擇并執行動作a(n)后，在第n+1時隙到達狀態

在無線通信系統中，用戶以任意模式的信道切換策略進行通信，干擾方執行Q學習算法學習用戶的信道切換規律。在執行算法的開始，干擾方的初始狀態設置為s0(cu1(0),cu2(0))，其中cu1(0)、cu2(0)分別為用戶1和用戶2在0-th的通信信道，由干擾方通過認知引擎的頻譜感知獲得。干擾方在0-th隨機選擇兩個信道cj1(0)、cj2(0)釋放干擾信號，并計算相應的回報值。之后的Twbss時間內，干擾方通過認知引擎的頻譜感知獲得當前時刻用戶1和用戶2的通信信道cu1(1)、cu2(1)，然后更新下一時隙的狀態為s1(cu1(1),cu2(1))，同時對Q值表中s0狀態下所有動作的Q值進行更新。算法依次迭代，最終在動態變化的環境中收斂到最優的干擾策略。詳細的算法流程如下：

初始化：

1.設置仿真時隙數為N（N>0），初始時隙為n=0。

2.設置Q學習參數γ，初始化Q值表Q(s,a)=0。

3.設置初始工作狀態為s0=(cu1(0),cu2(0))，其中cu1(0)、cu2(0)由認知引擎的頻譜感知獲得。干擾方隨機從所有信道中選擇兩個信道作為初始干擾信道cj1(0)、cj2(0)。

循環開始n=0,1,2,…,N-1

4.干擾方在cu1(n)、cu2(n)信道上對用戶通信進行干擾，干擾時隙長度為Tjam，根據式（1）計算相應的回報值rn。

5.干擾方通過認知引擎的頻譜感知獲得用戶當前時刻的通信信道cu1(n+1)、cu2(n+1)。

7.計算α=1/(1+Ta(n))。

8.根據式（7）并行更新所有狀態-動作對的Q值。

9.n=n+1。

10.更新狀態，令sn+1=sn。

循環結束

3 仿真結果

本節對所提基于隨機森林強化學習的智能干擾算法在MATLAB上進行仿真驗證，并分析其收斂性能。仿真中，假設用戶1以掃頻方式進行通信，用戶2以固定跳頻序列方式進行通信，其信道切換規律如表1所示。本文的主要系統參數設置如下：信道數M=16，學習速率α∈(0,1]，折扣因子γ=0.8。仿真時隙參數設置如表2所示。

表1 敵方用戶信道切換規律

表2 仿真時隙參數設置

圖4給出了系統采用不同干擾算法的干擾概率曲線。為了評估所提算法的性能，比較基于隨機森林強化學習的智能干擾算法、文獻[10]所提智能干擾算法和基于感知的隨機信道選擇算法的算法性能。圖4中干擾概率曲線是由干擾每20個時隙中成功干擾次數所占比例計算所得。通過圖4可以發現，與文獻[10]所提智能干擾算法以及基于感知的隨機信道選擇算法相比，本文所提算法干擾性能良好，且較文獻[10]中提出的智能干擾算法相比，收斂速度更快。

圖5中給出了干擾和用戶時頻圖。圖5（a）為在強化學習初期的干擾效果圖，開始階段干擾無法捕捉用戶的通信信道，只能通過隨機選擇的方式不斷探索規律，用戶被干擾的概率極低。圖5（b）為在強化學習末期（系統達到收斂條件）的干擾效果圖，圖中畫圈部分即表明用戶被干擾。經過在線學習，干擾找到了用戶的通信規律，基本上可以成功對用戶通信頻點進行干擾。

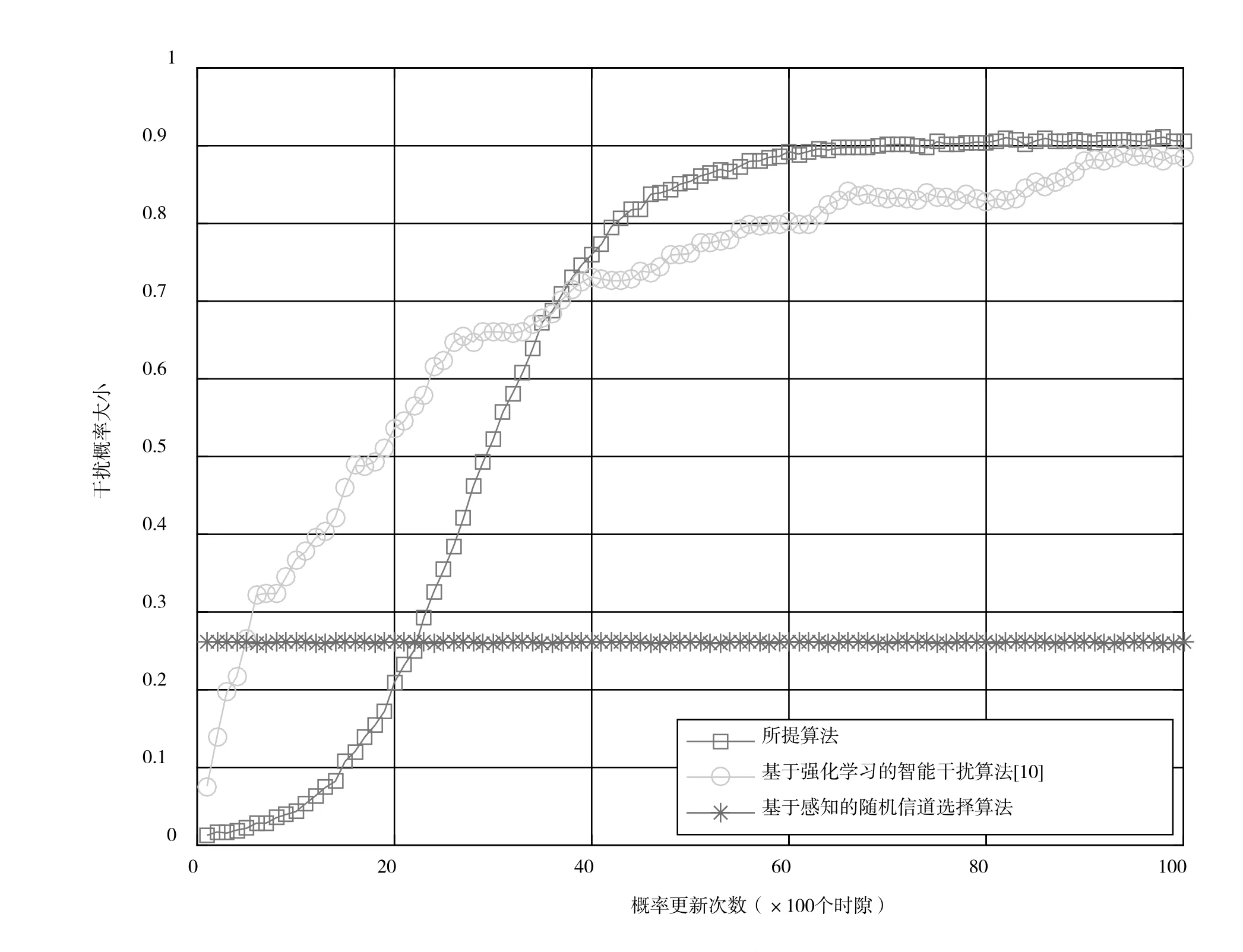
圖4 系統采用不同算法的干擾概率變化曲線

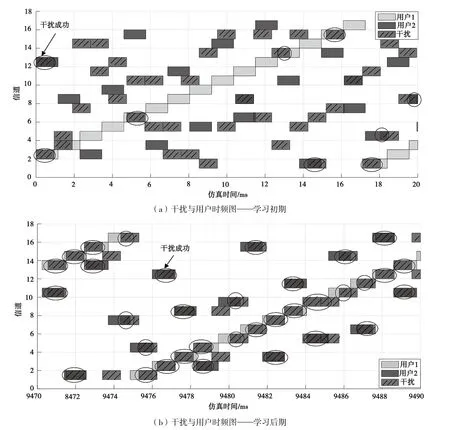
圖5 干擾與用戶時頻圖

4 結 語

本文研究了頻譜對抗環境中干擾智能決策問題。將干擾方的信道決策過程建模為一個MDP，提出了一種基于隨機森林強化學習的智能干擾算法。為了證明所提算法的有效性，本文將所提算法與文獻[10]所提智能干擾算法和基于感知的隨機信道選擇算法進行對比。仿真結果表明，所提算法的收斂速度最快，還可以根據當前的用戶通信環境成功學習到最優的干擾策略。本文為大規模無線網絡中的智能干擾研究提供了新的思路，未來將研究更加復雜的用戶通信策略，使通信對抗雙方更具有智能性。