基于VMD分解和小波閾值去噪的時差估計算法

摘 ?要： 為了提高時差定位算法的精度，提出了一種基于VMD分解和小波閾值去噪的時差估計算法。通過VMD分解將信號分解成若干個分量，再利用小波閾值去噪對各個分量進行去噪，最后將信號重構進行互相關得到信號的時延值。仿真結果表明，該方法優于直接小波閾值去噪的時差參數估計算法，具有更高的準確度和穩定性。

關鍵詞： 無源定位;到達時間差估計（TDOA）;變分模態分解（VMD）;小波閾值去噪;定位精度

中圖分類號： TN911.7 ? ?文獻標識碼： A ? ?DOI：10.3969/j.issn.1003-6970.2019.06.041

本文著錄格式：帥海峰. 基于VMD分解和小波閾值去噪的時差估計算法[J]. 軟件，2019，40（6）：176179+199

【Abstract】： In order to improve the accuracy of TDOA location algorithm， a TDOA estimation algorithm based on VMD and wavelet threshold de-noising is proposed. The signal is decomposed into several components by VMD， then each component is denoised by wavelet threshold de-noising. Finally， the signal is reconstructed and cross-correlated to obtain the value of TDOA. The simulation results show that the proposed method is superior to the TDOA estimation algorithm based on wavelet threshold de-noising， and has higher accuracy and stability.

【Key words】： Passive location; TDOA; VMD; Wavelet threshold de-noising; Location accuracy

0 ?引言

無源定位是通過接收有源設備發出的電磁信號，通過對信號進行分析和處理，從而獲得信號源設備的距離和方位等信息的定位方法[1]。無源定位由于自身不發出信號，具有極高的隱蔽性，星載無源定位系統的研制，更是實現了全天候、全球性的遠距離定位，在現代戰爭中，對于探測敵方軍事動向，有效保護我方力量具有極其重要的作用。

最常見的星載無源定位系統是三星時差定位系統。三星時差定位系統利用一顆主星與兩顆輔星接收地面信號源發出的信號，由于各個衛星與干擾源的距離不同，一對主星和輔星便可以根據信號傳輸的距離差得到一個時差值（TDOA），兩組時差值可以形成兩個雙曲面，雙曲面與地球表面相交于一點，該點便是信號源所在的位置[2]。時差定位算法由于算法簡單，計算量小，定位的實時性較高而受到廣泛應用。時差定位算法的精度主要取決于時差參數估計的精度，因此，如何提高時差參數估計的精度成為研究的熱點。

最基本的時差參數估計算法是互相關法，利用信號與噪聲、噪聲之間的相互獨立實現時差參數的估計[3]。但是在現實情況中，由于輔星接收到的信號源的旁瓣信號較弱，經常會出現一路信號的信噪比很低的情況，這時利用互相關法得到的時差參數的誤差就比較大。

在互相關法的基礎上，本文利用變分模態分解VMD和小波閾值去噪的相關理論，提出了一種新的時差參數估計算法——基于VMD和小波閾值去噪的相關時差參數估計算法。該算法首先將信號通過VMD劃分為多個IMF分量，再對每個分量進行小波閾值去噪處理，各分量處理完之后進行重構，對重構的信號進行二次相關法處理得到時差參數。通過VMD和小波閾值去噪，減少了噪聲對于原信號的影響，與互相關法相比，有效提高了低信噪比的條件下時差參數估計的精度。

本文的后續結構組成如下：第二部分，介紹了時差定位的原理和互相關法時差參數估計算法;第三部分介紹了基于VMD分解和小波閾值去噪的二次相關時差估計算法;第四部分通過仿真實驗驗證了算法的有效性;最后對本文的內容進行了總結。

1 ?三星時差定位系統

1.1 ?時差定位算法

時間延遲簡稱時差，即TDOA（Time Difference of Arrival），是指地面接收機由于接收到的同源帶噪信號之間因信號的傳輸路徑或距離的不同而引起的時間差。TDOA定位最早是應用在二維平面中的，在二維坐標系中，兩個接收站接收干擾源發出的射頻信號，由于接收站到干擾源的距離不同，通過對兩路信號的分析，就會產生一個TDOA值，一個TDOA值可以確定一個雙曲線。兩組TDOA所確定的雙曲線便可以相交于一點，干擾源就位于該交點范圍中[4]。將該理論引申到空間中，一個TDOA值可以確定一個雙曲面，雙曲面與地球面相交為一條曲線，兩組TDOA值在地球面上的曲線相交于一點，這個點就是干擾源的大致位置。三星時差定位系統的原理圖如圖1所示。

3 ?算法仿真分析

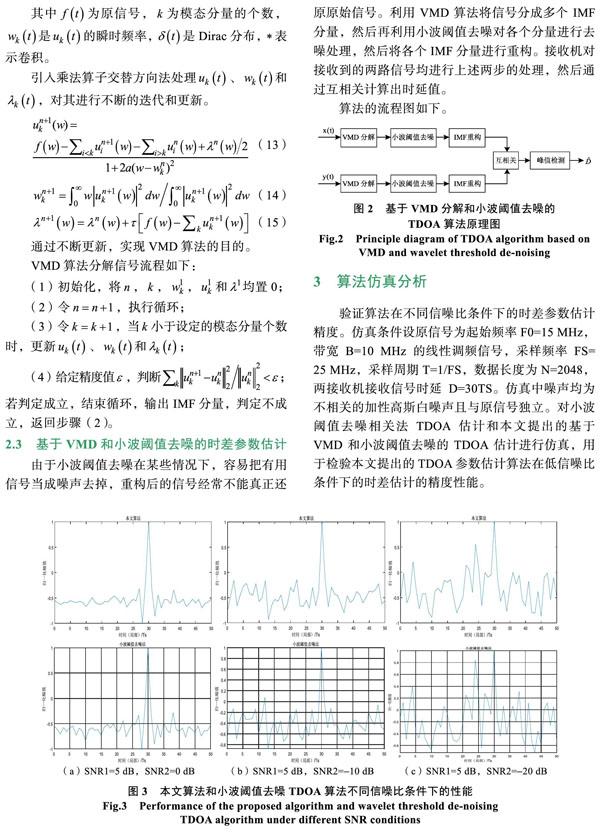
驗證算法在不同信噪比條件下的時差參數估計精度。仿真條件設原信號為起始頻率F0=15 MHz，帶寬B=10 MHz 的線性調頻信號，采樣頻率FS= ?25 MHz，采樣周期T=1/FS，數據長度為N=2048，兩接收機接收信號時延D=30TS。仿真中噪聲均為不相關的加性高斯白噪聲且與原信號獨立。對小波閾值去噪相關法TDOA估計和本文提出的基于VMD和小波閾值去噪的TDOA估計進行仿真，用于檢驗本文提出的TDOA參數估計算法在低信噪比條件下的時差估計的精度性能。

令主星接收信號的信噪比為5 dB，輔星接受的信號信噪比分別為0 dB、10 dB和20dB，分別觀察本文提出的時差估計算法和小波閾值去噪時差估計算法的性能。

由圖可知，當信噪比SNR1=5 dB不變時， SNR2從0 dB到10 dB到20 dB變化時，本文的算法和小波閾值去噪時差估計算法均能估計出準確的時延值。但是隨著SNR2的降低，兩種算法的估計性能都會下降，尤其是小波閾值去噪時差估計算法，在SNR2=20 dB時，相鄰的峰值已經接近最高點的峰值，估計性能下降明顯。

4 ?結束語

本文利用VMD分解和小波閾值去噪在互相關的基礎上進行時延參數的估計。仿真結果表明，本文提出的方法可以實現低信噪比條件下時差參數準確估計，相比于小波閾值去噪時差估計算法，通過VMD分解可以避免將原信號消除，更加準確的還原出原信號，從而得到更加準確的時差值。但是本文算法的計算量較大，無法滿足無源定位的時效性要高的要求，在之后的研究中，將針對算法的快速性進行改進研究。

參考文獻

[1] 江文穎. 無源定位中時差估計及定位方法的研究與實現[D]. 電子科技大學， 2015.

[2] 龔峰， 宋熠. 室內定位技術研究[J]. 軟件， 2016， 37（4）： 08-12.

[3] 楊建輝， 劉玉紅， 王逸軒. 基于廣義互相關和多項式擬合的TDOA時延估計方法[J]. 蘭州交通大學學報， 2016， 35（4）： 40-43.

[4] 陳斌， 鄭江龍， 勾學榮， 等. 一個時空定位方法[J]. 軟件， 2015， 36（2）： 59-63.

[5] 竇慧晶， 王千龍， 張雪. 基于二次相關的廣義互相關時差估計算法[J]. 北京工業大學學報， 2016， 42（2）： 197-202.

[6] 喻偉， 趙立業. 基于CEEMD 和小波包變換的重力數據信噪分離方法[J]. 軟件， 2015， 36（2）： 49-54.

[7] 王賽男， 邢冬梅. 基于MATLAB 的小波閾值濾波與應用[J]. 軟件， 2015， 36（10）： 102-104.

[8] 吳光文， 王昌明， 包建東， et al. 基于自適應閾值函數的小波閾值去噪方法[J]. 電子與信息學報， 2014（6）.

[9] Chen L， Xie B. A new signal denoising method based on wavelet threshold algorithm[C]//IEEE International Conference on Computer & Communications. 2017.

[10] Dragomiretskiy K， Zosso D. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing， 2014， 62（3）： 531-5.

[11] 常貴春， 葉俊勇， 李陽. 基于EEMD 樣本熵和SVDD 的在役錨固螺桿故障診斷研究[J]. 軟件， 2015， 36（2）： 20-26.