等價條件平差模型的方差-協方差分量最小二乘估計方法

劉志平，朱丹彤，余 航，張克非,2

1. 中國礦業大學環境與測繪學院, 江蘇 徐州 221116； 2. 皇家墨爾本理工大學空間科學研究中心，澳大利亞 維多利亞州 墨爾本 3001

隨著現代測量技術的發展，測量數據處理的對象已經由單一同類觀測數據轉變為多源、多類或同類多因素的異方差結構觀測數據，在這種情況下隨機模型的準確性對參數解估計的統計特性具有重要影響[1-2]。方差-協方差分量估計能夠極大地改善隨機模型不精確的問題，從而成為國內外學者關注的焦點，并形成了一整套的理論框架[3-8]。近年來主要理論研究包括：①以平差結果之一的殘差向量為基本輸入量的殘差型VCE方法，如Helmert法[1-2,7]、最小二乘方差分量估計法(簡稱LS-VCE)[9-11]、MINQUE法[12]、BIQUE法[13]、MLE-VCE法[14]、等效殘差法[15-16]及EIV模型的VCE方法[4,8]等；②以等價條件閉合差為基本輸入量的解析型VCE方法，如VCE-ECM法[17-18]。近年來的主要應用研究有：文獻[19—20]研究了常規導線控制網中角度觀測值與距離觀測值的定權問題；文獻[21—22]探討了GNSS觀測值隨機模型的精化問題；文獻[23—24]研究了坐標轉換中不同公共點坐標的精度問題；文獻[11,25—26]開展了GNSS站坐標時間序列的噪聲估計及評價研究。

大量研究表明，LS-VCE方法[9-10,15]可導出Helmert、MINQUE、MLE-VCE等方法的方差-協方差分量估計公式，具有最優無偏特性。與此同時，基于等價條件平差模型的VCE-ECM法[17-18]以等價條件閉合差作為基本輸入量，摒棄了平差值求解或殘差估計過程。鑒于此，本文從方差-協方差分量最小二乘估計準則和等價條件平差模型出發，利用等價條件閉合差的二次型構造方差分量估計公式，進而將方差分量估計方程變換為線性Gauss-Markov形式并建立了基本估計方程；然后，顧及矩陣拉直、半拉直算子和Kronecker積的性質進行化簡，導出了基于等價條件閉合差的方差-協方差分量最小二乘估計公式(least-square variance-covariance estimation based on the equivalent condition misclosure)，簡稱為LSV-ECM法。在此基礎上，證明了本文LSV-ECM法與殘差型VCE方法的等價性，定量分析了LSV-ECM法、Helmert法和LS-VCE法的計算復雜度，以邊角網平差和中國區域GNSS站坐標時序建模實例驗證本文方法的正確性和高效性。

1 等價條件閉合差的方差分量最小二乘估計

1.1 等價條件平差模型

設概括平差模型為

(1)

式中，A、[BTCT]均為行滿秩系數矩陣；W為具有參數的條件方程閉合差；Z為限制條件方程閉合差；DL為觀測值L的方差陣；V、x分別為待求的殘差與參數向量；下標c、s分別為條件方程個數和限制條件方程個數；n、u分別為觀測數和參數個數；平差模型自由度r=(c+s)-u。

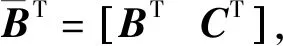
(2)

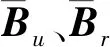
(3)

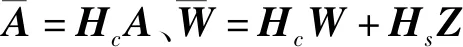
1.2 方差-協方差分量最小二乘估計方法

假設概括平差模型式(1)中隨機模型DL可表示為

(4)

式中，∑(·)表示累加運算；k為方差-協方差分量的個數；Qi為第i個協因數分量矩陣。

(5)

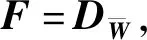
(6)

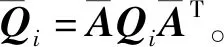
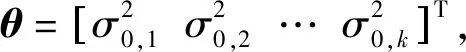
(7)

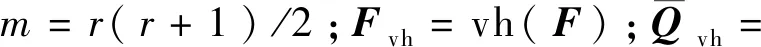
(8)

(9)

式中，D為復制矩陣(duplication matrix)[9]，也即半拉直算子與拉直算子的映射矩陣

(10)

分析可知，式(8)—式(10)含有大量的高維矩陣迭代運算(r2階)，因而需進一步簡化矩陣運算。考慮到矩陣拉直算子vec(·)、Kronecker積?和矩陣跡算子tr(·)具有如下性質[9]

vec(T)T·(U?S)·vec(VT)=tr(UVST)

(11)

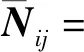
(12)

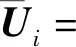
(13)

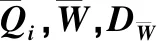
參量模型條件平差具有參數的條件平差間接平差附有限制的間接平差B=0,C=0C=0A=-I,C=0A=-IQiAQiATHAQiATHTHQiHTHcQiHTcWWHWHWHcW+HsZDWADLATHADLATHTHDLHTHcDLHTc

現有文獻已證明殘差型VCE方法之間的等價性，并形成了一套較為完整的理論框架。通過概括平差因子矩陣R也可以證明本文LSV-ECM方法與殘差型VCE方法的等價性。對于概括平差模型，LSV-ECM法與Helmert型通用VCE方法[7](簡稱通用Helmert法)等價；對于間接平差模型，LSV-ECM法與LS-VCE法[9,11]、基于等效殘差的LS-VCE法[15]等價；對于具有參數的條件平差模型，LSV-ECM法與文獻[10]相應算法等價。為節省篇幅，這里僅給出LSV-ECM法與通用Helmert法[7]等價關系的證明過程。

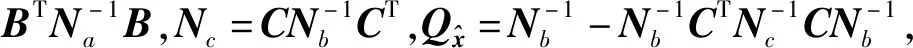
(14)

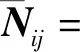
(15)

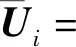
(16)

分析對比式(15)—式(16)和式(12)—式(13)可知，LSV-ECM方法可以導出通用Helmert法[7]，等價性得證。其次，殘差型VCE方法(如Helmert法、LS-VCE法等)均以殘差向量為輸入量，而本文LSV-ECM法以等價條件閉合差為輸入量，后者實現了平差值求解(殘差為平差結果之一)與隨機模型估計的分離。再次，等價條件閉合差維數低于殘差向量維數，且前者為不需求解的已知量，因此計算效率方面明顯優于前者。

表2 不同VCE方法的計算復雜度

Tab.2 A comparison of computational complexities of different VCE methods

2 應用結果及分析

2.1 邊角網平差

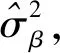
方案1：分別采用通用Helmert法[7]、LS-VCE法[9,11]、本文LSV-ECM法進行方差分量估計和參數平差計算。其中測角和測邊單位權中誤差的迭代初值均取先驗中誤差，迭代終止條件為測角和測邊的單位權中誤差相等。

方案2：在方案1的基礎上，剔除含有粗差的12號角度觀測值和16號邊長觀測值[18]，基于余下的16個觀測值進行方差分量估計和參數平差計算。

按上述方案分別進行計算，統計不同方法迭代收斂時的方差分量估值、參數估值及其中誤差。另外，為避免單次計算的隨機誤差，將上述方案重復計算100次，并統計LS-VCE法和本文LSV-ECM法相對于通用Helmert法的耗時比值Tratio，所得結果如表3所示。

表3 不同VCE方法的估計結果

從方案1方差分量和待估參數的估計結果看，3種結果完全相同，表明3種方法均能獲得一致的估計結果。同時比較3種方法的計算效率，通用Helmert法和LS-VCE的計算效率處于同一水平，本文所提出的LSV-ECM法的計算效率最高，其計算時間約為通用Helmert法的65%，較通用Helmert法和LS-VCE法均有明顯提升，從而驗證本文方法的有效性。

方案2中同樣可以驗證本文所提方法的正確性和有效性，不再贅述。同時，方案2在剔除兩個粗差觀測值以后，兩類觀測值的單位權方差、參數的估計精度均有較大提升，表明3種方差分量估計方法都無法抑制粗差影響，必須引入質量控制方法進行粗差識別與剔除。

2.2 GNSS站坐標時序建模

為進一步檢驗本文LSV-ECM法的正確性和高效性，選用中國大陸構造環境監測網絡(crustal movement observation network of China，CMONOC)中16個長期線性趨勢穩定的GNSS基準站2005.0014(DOY)～2015.0014(DOY)共10年的原始坐標時間序列進行噪聲特性分析(方差-協方差分量估計)和三維運動速度估計(平差參數計算)，測站位置分布如圖1所示。

GNSS站坐標時序的觀測方程和隨機模型分別為[11]

y(ti)=a+bti+ccos(2πti)+dsin(2πti)+

ecos(4πti)+fsin(4πti)+vi

(17)

(18)

式中，ti是以年為單位的時間序列歷元點；a為常數項；b為線性速度項；c、d組合表示全年性周期運動；e、f組合表示半年性周期運動；vi為殘差；σWN、σFN為所求的噪聲分量大小；QWN、QFN分別為白噪聲和閃爍噪聲的協因數陣，具體形式見文獻[11]。

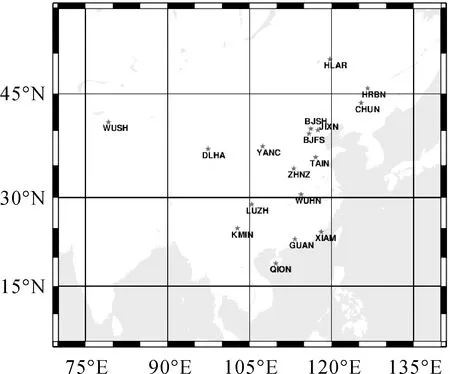
圖1 CMONOC所選測站分布Fig.1 Geographical distribution of selected stations in the CMONOC network

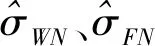
表4 噪聲分量(WN,FN)估計結果

注：高斯白噪聲(WN)的單位為mm；閃爍噪聲(FN)的單位為mm/a0.25

對比表4中通用Helmert法、LS-VCE法和LSV-ECM法的計算結果可知，3種方法所得的噪聲分量結果完全相同，驗證了本文方法的正確性。同時，對比3種方法的計算效率可知，通用Helmert法與LS-VCE法基本一致，而本文LSV-ECM法有較大提高，三維方向計算時間比分別為通用Helmert法的74.0%、73.8%、72.1%，表明本文方法的高效性。

由表4噪聲分量的估計結果可知，白噪聲分量均遠小于閃爍噪聲分量，表明有色噪聲為中國區域GNSS站坐標時間序列的主要噪聲，在參數估計時若直接采用白噪聲模型會導致估計結果有偏，并會產生較高的虛假估計精度。另外，對比不同方向的噪聲分量估計結果，北方向和東方向的噪聲分量相差不大，且量級較小，94%和88%的測站白噪聲分量在1 mm以內，50%的測站閃爍噪聲分量在3 mm/a0.25以內，而豎直方向的噪聲分量遠高于水平方向，這與現有結論相一致，約有56%的測站白噪聲分量在3 mm以內，31%的測站閃爍噪聲分量在9 mm/a0.25以內。

為進一步分析噪聲大小與經緯度之間的關系，繪制了白噪聲分量和閃爍噪聲分量隨經緯度的變化情況。由于噪聲大小與緯度相關性較強、與經度相關性較弱，為節省篇幅，此處僅討論噪聲大小與緯度變化的關系，見圖2。從圖2可以看出，水平方向的白噪聲和閃爍噪聲分量大小較為平穩，豎直方向的噪聲大小波動較大。從整體趨勢上看，白噪聲和閃爍噪聲大小隨緯度變化的趨勢較為明顯。具體表現為：噪聲大小隨緯度增加而逐漸減小，減少過程中有輕微波動，且在中緯度地區有翹尾現象。該現象原因分析可能是GNSS的GDOP值隨緯度增大而降低[28]，從而使噪聲分量表現出隨緯度增加而減小的現象，而且噪聲分量在中緯度地區呈現一定的翹尾現象。

此外，為檢驗方差-協方差分量估計結果的正確性和有效性，以CMONOC的公布數據(http:∥www.cgps.ac.cn/cgs/index.action)作為對比參考值，表5統計了中國區域GNSS站的三維運動速度和不確定度。由該表可知，中國區域不同站點水平方向均呈現東南方向運動趨勢，這與亞歐板塊的整體運動趨勢相一致，但豎直方向運動變化差異性較大，其中約40%的測站呈現下沉趨勢。對比本文結果與CMONOC的公布結果，除JIXN、HLAR站N方向，KMIN、GUAN站E方向，CHUN、BJFS站U方向以外，其余計算結果均在2倍中誤差范圍內。此外，參照文獻[29]的計算結果，對比發現除CHUN站U方向外，其余測站的計算結果與本文結果具有較好的相符性，進一步驗證了本文方法的正確性。需要指出的是，CHUN站U方向的差異性可能是數據預處理和共模誤差提取策略不同所致。

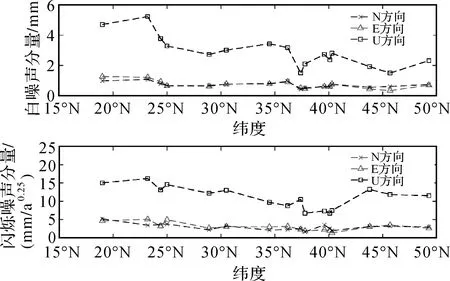
圖2 噪聲分量大小與緯度的關系Fig.2 The relationship between noise components and latitude

3 結 論

本文基于等價條件平差模型和最小二乘準則，利用等價條件閉合差的二次型構建方差-協方差分量估計方程，并通過矩陣半拉直算子將其變換為線性Gauss-Markov形式，進而顧及矩陣拉直算子、半拉直算子和Kronecker積運算性質，導出了基于等價條件平差模型的方差-協方差分量最小二乘估計公式，簡稱LSV-ECM法。該方法實現了平差值求解(殘差為平差結果之一)與隨機模型估計的分離，有效兼顧了等價條件閉合差(已知)和最小二乘的特性。邊角網平差實例的結果表明，本文的LSV-ECM法與通用Helmert法、LS-VCE法的結果完全相同，但計算效率更高，驗證了該方法與殘差型VCE方法的等價性和計算高效性。

分析指出了方差-協方差分量估計方法相較于常規GNSS-MLE法進行GNSS站坐標時間序列噪聲分析的優勢，并利用LSV-ECM法、通用Helmert法、LS-VCE法計算分析了中國區域16個GNSS站坐標時間序列在WN+FN模型下的噪聲估計和站點速度。估計結果表明，有色噪聲是中國GNSS站坐標時序的主要噪聲，且白噪聲和有色噪聲分量隨緯度增大而減小，速度估計結果與陸態網絡的公布結果基本一致，水平方向的整體運動趨勢呈東南方向，而豎直方向的運動趨勢差異性較大。因此，計算結果也進一步驗證了本文LSV-ECM法的正確性和高效性。

表5 站點運動速度和不確定度