轉子系統模態綜合法

李文浩

(哈爾濱電機廠有限責任公司，黑龍江哈爾濱 150040)

0 引言

結構系統動力分析通常采用整體結構有限元方法，可用于復雜的大型結構分析，例如蒸汽輪機，飛機，車輛，船舶等整體結構，但該方法計算規模大，計算時間長，所使用的磁盤空間和計算機系統太大。在有限元方法用于更高頻率的振動分析時，需要將結構分為大量的單元，來得到詳細的應力特性和位移。此時，模型里節點有數十萬或是數百萬個自由度，要直接解析這么大的結構模型是非常困難的[1]。即使可以進行分析，也需要花費大量時間并且效率極低。

模態綜合方法是一種降低產生自由度的方法。此方法能夠使大型模型簡化變小，首先對每個子結構進行模態解析，再完成模態綜合。因為只用了每個子結構的低階模態，因此，大幅降低了整體模型結構的動力模型的自由度。并且，還能在不同機器上模態分析每個子結構，從而提升計算的速率[2]。

本文將著重論述常用于轉子動力學中的模態綜合方法。

1 模態綜合法的基本思想理論和步驟

1.1 基本思想和理論

此方法的基本原理是根據其結構特征，將一個復雜的結構劃分為多個子結構。再使用離散化方法對各個子結構進行多個力學解析。基于每個子結構的結點位移坐標，完成坐標變換和子結構進行分組。只需將每個子結構的模態坐標分組到整體結構坐標中，由子結構連接條件，執行第二坐標轉換，從而清除非獨立坐標，獲得表示整個結構運動的廣義坐標。這樣，組集得到的模型的獨立廣義坐標的數量大大降低[2]。從而能得到整個系統的動力方程，此方程以獨立的模態坐標表述。通過這種方式，求解低階系統的動力學方程要容易得多[3]。由于大大降低了自由度，機器時間和存儲器顯著減少，傳遞矩陣法所需的機器時間較少，計算精度也非常令人滿意。

子結構方法中最常用和最成熟的就是模態綜合法，Raylei-Ritz方法，是動態子結構的理論基礎。

1.2 模態綜合法的基本步驟

模態綜合法包括以下兩個步驟[3]：

(1)基于每個子結構的結點位移坐標，完成坐標變換和子結構進行分組。

(2)由子結構連接條件，執行第二坐標轉換，從而清除非獨立坐標，獲得表示整個結構運動的廣義坐標。

模態綜合方法遵循有限元方法，首先分析每個局部子結構，然后通過某種方法進行整體分析。通過每個子結構模態解析，獲得一個“假設模態”，此“假設模態”可以根據一定的原則很好地表述整個模型結構的振動[4]，然后使用假設模態分析法解析整個模型結構的振動。

假設某個簡單的無阻尼自由振動結構，將原始的結構化為兩個子結構α和β，各個子結構自由度包括界面自由度與內部自由度[5]。兩個子結構的自由度，以矢量形式表述的物理坐標為

(1)

由力的對接條件和界面連續性條件，得

(2)

在簡單疊加之后，獲得整個結構的動能為

(3)

系統的總勢能為

(4)

其中，[mα]、[mβ]和[kα]、[kβ]是質量矩陣與剛度矩陣，分別對應于α和β子結構的物理坐標{uα}和{uβ}。解析每個子結構的動力特征，選擇合適的分支模態形成模態矩陣[φα]與[φβ]，并對β和α子結構進行模態坐標變換可得

{uα}=[φα]{pα}

(5)

{uβ}=[φβ]{pβ}

(6)

其中，{pα}和{pβ}分別是兩個子結構的模態坐標。子結構的自由度遠大于分支模態數量。等式(5)和(6)通常被稱為第一坐標變換，將等式(5)和(6)代入等式(3)和(4)，由分支模態坐標表述的系統動能和勢能即為

(7)

(8)

其中

[mα]=[φα]T[mα][φα]，
[mβ]=[φβ]T[mβ][φβ]

(9)

[kα]=[φα]T[kα][φα]，[kβ]=[φβ]T[kβ][φβ]

(10)

(11)

顯然，因為存在等式(2)表示的條件約束，系統的模態坐標中，不是所有坐標都是獨立的，因此由等式(7)、(8)表述的系統勢能和動能表達式代入第二類拉格朗日方程，以獲得結構系統運動方程[6]。僅在{p}去除了獨立模態坐標時，才可以代入第二類拉格朗日方程中。

可以從每個分支的模態坐標變換方程(5)和(6)獲得。

(12)

(13)

由此可得

(14)

(15)

由界面位移連續條件(2)式，可得

或寫為

(16)

簡記為

[C]{p}={0}

(17)

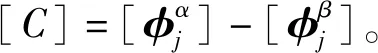
(18)

所以，等式(17)也可表述為

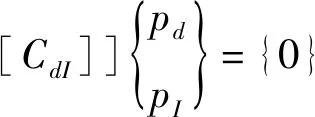
(19)

即得

{pd}=-[Cdd]-1[CdI]{pI}

(20)

所以有

(21)

[S]是獨立坐標變換矩陣

(22)

上述公式(21)是第二坐標變換。所以獨立廣義坐標{q}={pI}可用于表述該結構的勢能和動能

(23)

(24)

其中

[M]=[S]T[m][S]

(25)

[K]=[S]T[k][S]

(26)

因此，獲得了無阻尼結構系統的自由振動方程

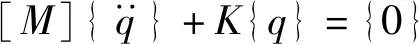
(27)

對應的系統廣義特征值可表示如下

([K]-ω2[M]){A}={0}

(28)

這是綜合每個子結構得到的新方程。等式階數與每個分支結構模態的總和數減掉子結構連接坐標的數量相等。

普通的動力學方程，同樣能夠獲得具有減小的自由度的等式方程

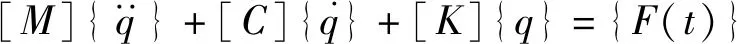
(29)

式中，由等式(27)得出[M]，[K]，其中[C]與{F(t)}可表示為

[C]=[S]T[c][S]
{F(t)}=[S]T{p}

(30)

為了描述空間結構的構造，即其運動和變形狀態，通常使用兩種類型的廣義坐標：“物理坐標”和“模態坐標”。描述結構中每個點的幾何位置坐標為物理坐標，是表述每個模態組件大小的坐標為模態坐標。這里使用術語“模態”而不是“振動類型”，因為“振動類型”是結構的變形形式作為主要振動。“模態”的概念是模式概念的概括，它不僅包含結構主振動的變形形式，它還包括由某些特定外力或關節位移產生的結構的靜態變形形式。

轉子動力學模態綜合方法的基本思路和步驟基本相同，只是如何劃分子系統，如何選擇子系統的Ritz基礎，如何處理綜合中對接條件的發展，高效的模態綜合技術是用很少的Ritz基來實現令人滿意的精確度。子結構振動分析中，已發展出Ritz基選取的各種辦法，如：約束子系統方法，自由子系統方法，組件假設形式方法。

2 總結

模態綜合法有許多優點：

(1)顯著節省計算機計算資源和時間，從而提升計算效率。

(2)此方法為子結構技術，能夠計算超大的模型，同時，計算精度高。

(3)能夠靈活的修改大系統中子系統設計。如果修改了子系統結構，則只需要重新計算修改后的子系統，再收集每個子系統。此過程中，不需要重新計算整個結構，降低了計算的時間。

因此，對于復雜大型結構，如：水輪機轉子、船舶、汽車、飛機等結構，利用模態綜合法分析結構，能夠更好地解決計算速率和精度問題。