基于等效電路模型的基片集成波導濾波器快速設計方法

馬 亮，倪大海，李 江，鄺小樂

(1.中國船舶重工集團公司第七二四研究所，南京 211153；2.中國船舶重工集團公司第七二三研究所，江蘇 揚州 225101)

0 引 言

基片集成波導(SIW)濾波器是近年來備受關注的一項技術。它類似于傳統矩形波導濾波器，具有低損耗、高Q值等優點。同時，基片集成波導濾波器尺寸小、成本低，易于制作，易于實現與其他平面器件互聯，在一塊PCB板上構成一個系統，實現系統的高集成度和小型化。設計SIW濾波器首先根據指標得到諧振頻率和耦合系數，再由相關理論得到初始尺寸值，最后在全波仿真軟件中不斷優化各個尺寸得到需要的濾波器響應。當優化的參數過多時，仿真優化需要較為漫長的過程。由于每次全波仿真耗時長，設計SIW濾波器需要耗費大量的時間。

本文提出一種基于等效電路模型的SIW濾波器快速設計方法，可根據等效電路模型獲知當前狀態下SIW濾波器實際的諧振頻率和耦合系數，進而得知各個尺寸參數的調整方向。采用這種方法只需6次全波仿真即可設計一款工作在21 GHz、帶寬為1 GHz的濾波器。

1 基本理論

1.1 SIW諧振腔

圖1所示為典型的單層SIW諧振腔。它是由敷于介質基片上下的金屬板和嵌入基片的金屬化通孔構成的封閉結構，金屬通孔的直徑為d，孔與孔之間的距離為p。當通孔直徑與孔間距滿足d<0.2λg，d/p≥0.5時(λg為電磁場在介質中的波長)，電磁場被束縛在其中，向外界泄露能量極低[1]。將單個SIW腔接上輸入/輸出端口，對其頻率響應進行仿真(如圖2所示)。SIW腔表現出帶通的特性，并且帶內插損很低。

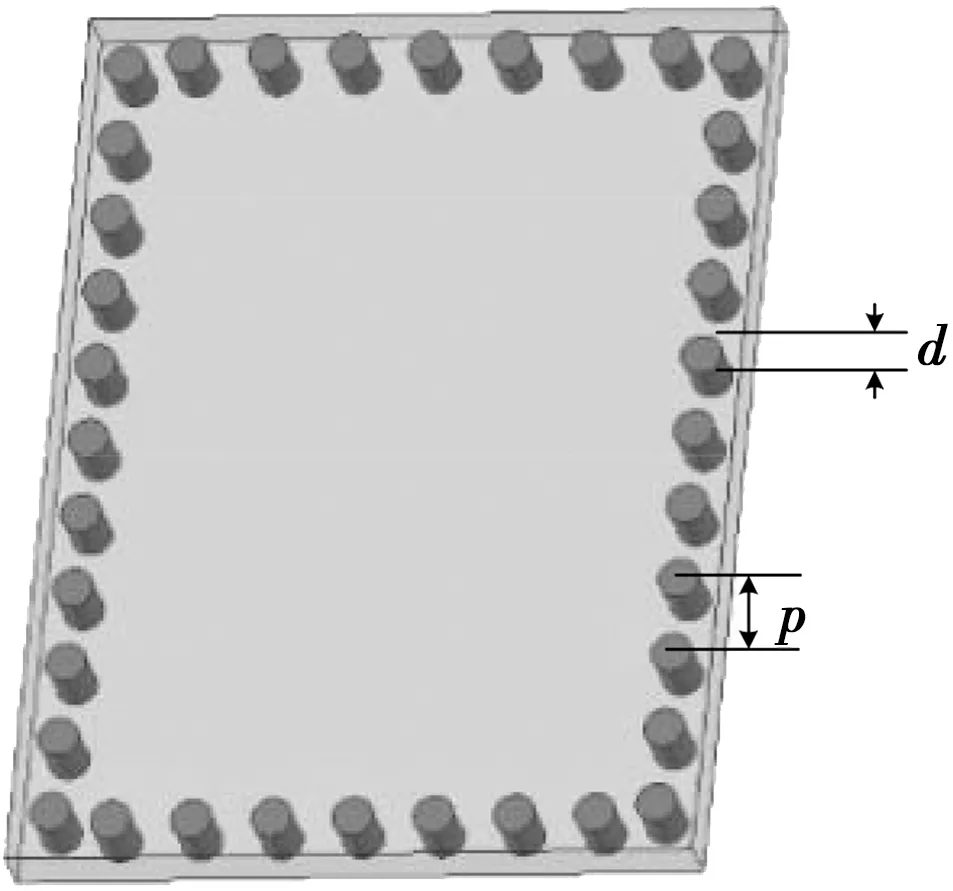
圖1 SIW諧振腔

SIW腔與傳統矩形波導腔結構、特性都極為相似，已有的矩形波導的設計經驗及方法可以直接應用于SIW的設計。對于長為L、寬為W的SIW腔，可以將其等效為一矩形波導，等效出的矩形波導長為Leff， 寬為Weff，兩者的尺寸滿足如下的關系[2]:

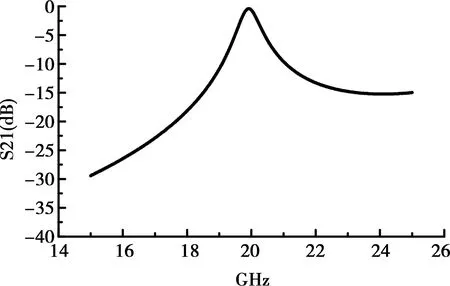
圖2 單個SIW諧振腔的頻率響應

(1)

(2)

參考矩形波導相關理論[3]，則對于SIW腔中的TEm0n模式(m、n為整數)其諧振頻率為

(3)

其中，c0為真空中的光速，εr為介質的介電常數。在實際設計濾波器時，腔體的諧振頻率可以用商用軟件(如HFSS、CST等)采用本征頻率仿真獲得。

1.2 耦合系數

現代濾波器設計常用的方法是耦合矩陣法，比較適用于帶通濾波器的設計。用這種方法需要知道各個腔的諧振頻率、腔與腔之間的耦合系數及外部品質因數[4]。耦合系數是濾波器設計中的重要參數。它定義為耦合能量與存儲能量之間的比值。在實際濾波器設計中采用成熟的商業軟件提取耦合系數，在軟件中建立雙腔模型，利用軟件的本征模分析可得到電路頻率響應中兩個諧振峰所對應的兩個頻率，分別為f1和f2，則耦合系數可以由下式計算：

(4)

此種方法提取的耦合系數只能得出絕對數值，至于該耦合是負耦合還是正耦合需要設計者通過腔的結構加以判斷。

1.3 等效電路

SIW諧振腔可用LC并聯諧振電路進行等效，如圖3(a)所示，其中f代表諧振腔的中心頻率。耦合窗可用移相器進行等效，如圖3(b)所示，其中k是耦合窗的耦合系數。

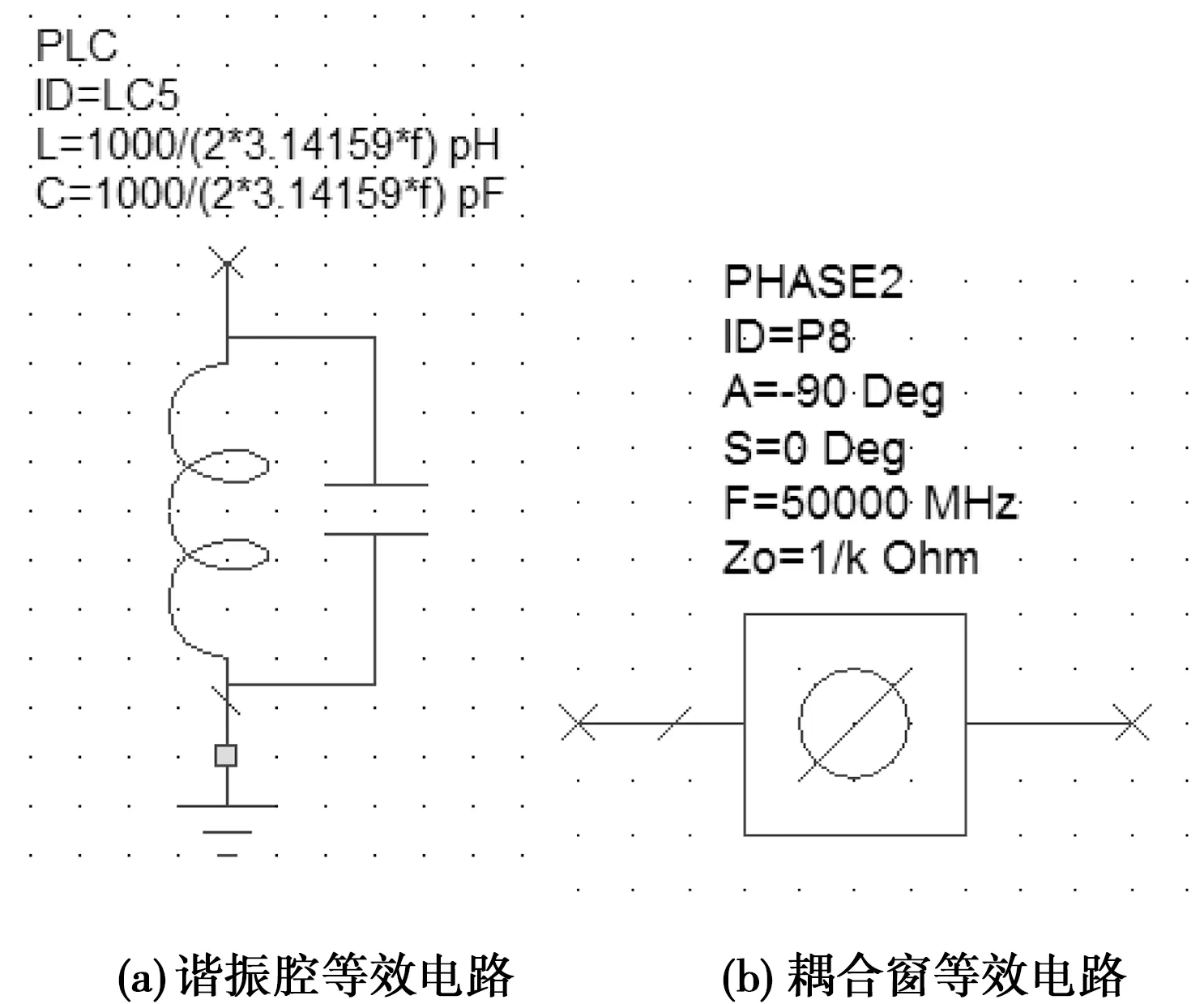
圖3 AWR仿真軟件中的等效電路

2 六階SIW濾波器設計

2.1 濾波器結構

所要設計的六階級聯型SIW濾波器的拓撲結構如圖4所示。該濾波器左右結構對稱。所用的介質基片為Rogers RT/Duroid 5 880，介質的介電常數為2.2，損耗角正切為0.0009，厚度選為0.508 mm，金屬通孔的直徑為0.4 mm，孔間距設為0.8 mm。

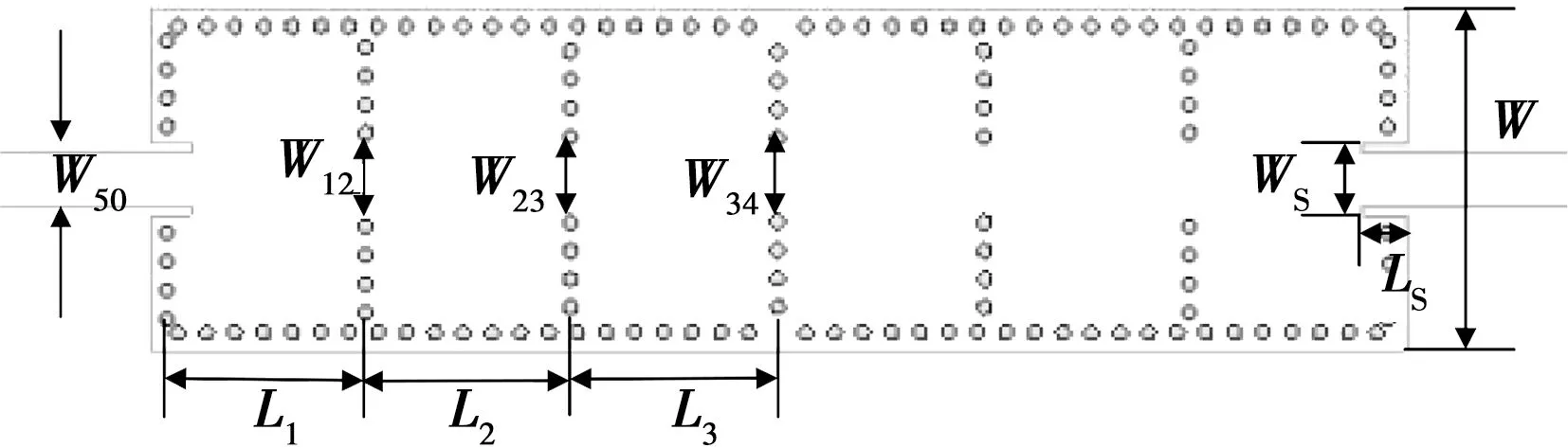
圖4 六階SIW濾波器幾何結構

與濾波器對應的電路級模型如圖5所示。該模型共有7個優化參數，分別是3個諧振頻率、3個耦合系數、1個外部品質因數。

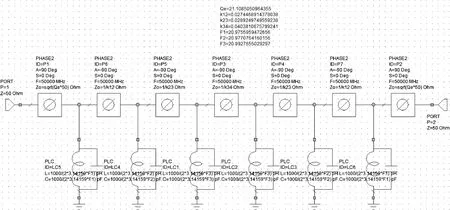
圖5 SIW濾波器電路模型

設圖4所示的濾波器全波仿真的傳輸系數和反射系數分別為S21F、S11F。圖5所示的等效模型的傳輸系數為S21C。圖5為理想模型，沒有考慮各種損耗。由全波仿真結果可以計算實際濾波器的損耗為

D=10*lg(|S21F|2+|S11F|2)

(5)

設理想電路模型和全波仿真的傳輸系數誤差為ε，則

ε=10*lg(|S21C|2)-10*lg(|S21F|2)+D

(6)

優化等效電路模型的7個參數以使ε盡可能小，使電路級的響應與實際全波仿真響應相一致。得出的7個參數值即為實際濾波器當前尺寸參數下各諧振頻率、耦合系數的值。為達到預定的值，需要優化濾波器的尺寸。

2.2 濾波器設計

設定濾波器的中心頻率為21 GHz，帶寬1 GHz，帶內反射系數小于-20 dB。根據以上指標，可綜合出所需的耦合矩陣[5]，其中一個可能的解是

(7)

耦合矩陣M意味著各個腔體的諧振頻率如下：

f1=f2=f3=f4=f5=f6=21 GHz

(8)

以及各個腔體之間的耦合系數和外部品質因數：

k12=k56=0.04，k23=k45=0.029

k34=0.0278， QE=20.91

(9)

圖4中的濾波器各尺寸初始值設置如表1所示。

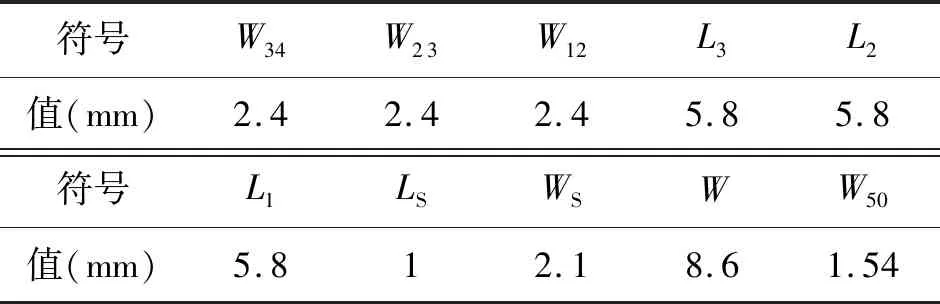
表1 SIW濾波器尺寸初值

對該濾波器進行全波仿真，并優化等效電路模型的參數，使兩者響應相一致。全波仿真與等效電路響應如圖6所示，兩者有較好的吻合度。此時，等效電路的7個參數值如表2所示。

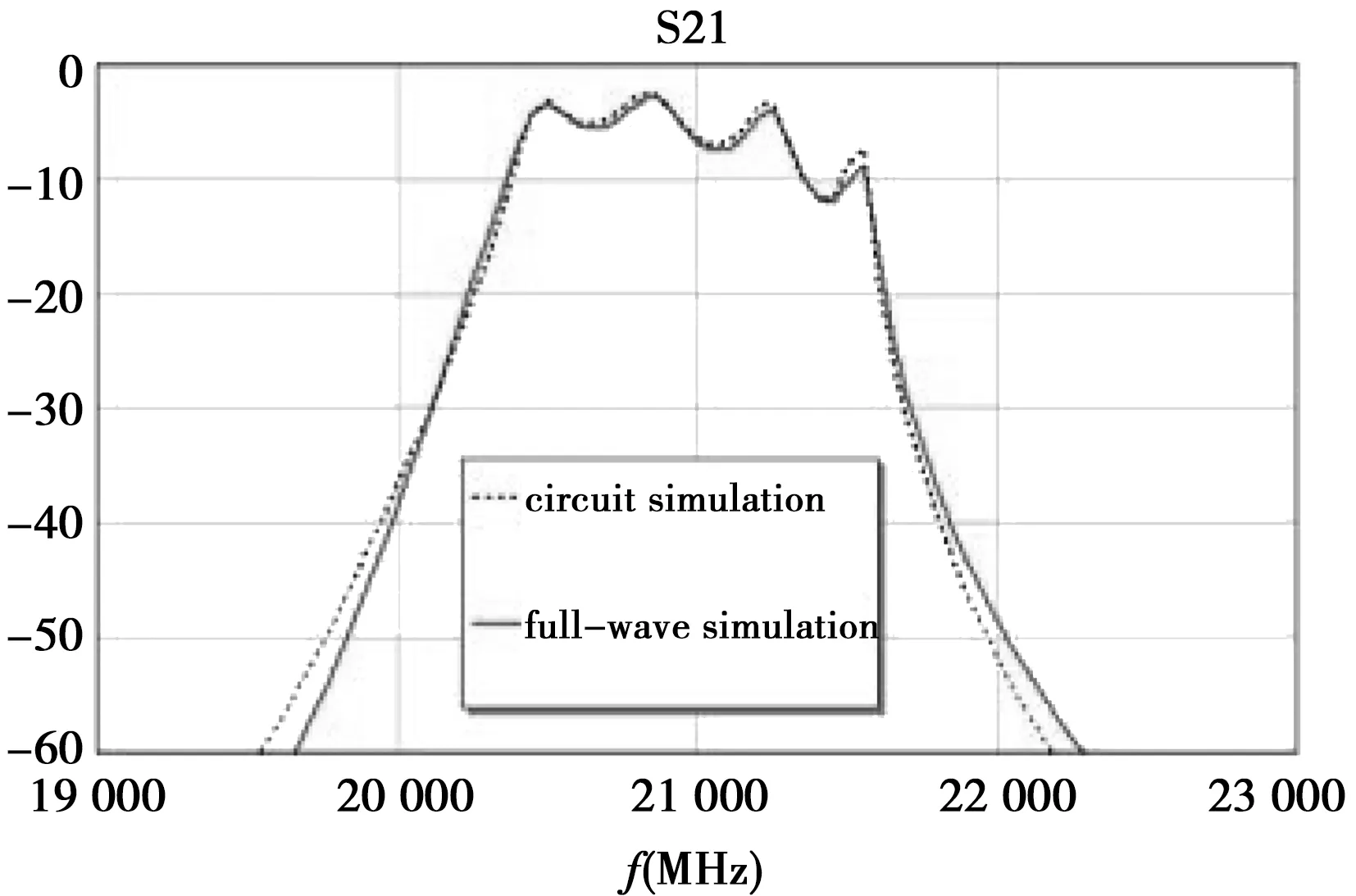
圖6 全波仿真與電路模型響應對比

表2 濾波器對應的諧振頻率、耦合系數

將表2數據與式(8)、(9)進行對比可知，6個腔的諧振頻率都偏小，需要減小腔的尺寸，可主要通過減小L1、L2、L3的值實現。腔1與腔2之間的耦合系數偏小，需要增大W12的值；腔2與腔3、腔3與腔3之間的耦合系數偏大，需要減小W23、W34的值。諧振腔的諧振頻率主要取決于腔的尺寸，但也會受到耦合窗大小的影響。耦合系數主要取決于耦合窗大小，但腔尺寸變化會引起耦合系數微小變化。整個濾波器設計過程是一個不斷迭代、反復優化的過程。

3 濾波器優化過程

濾波器優化是一個迭代的過程，如圖7所示。

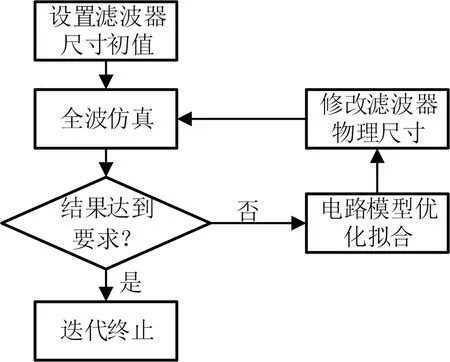
圖7 濾波器優化過程流程圖

該設計過程把耗時的全波仿真優化轉化為快速的電路級優化，一共進行了6次全波仿真即可得到性能良好的SIW濾波器。濾波器物理尺寸變化如表3所示。圖4中的WS、W、W50在優化過程中不作變動。

表3 濾波器尺寸變化過程

在優化過程中，圖5中的電路模型參數的變化過程如表4所示。

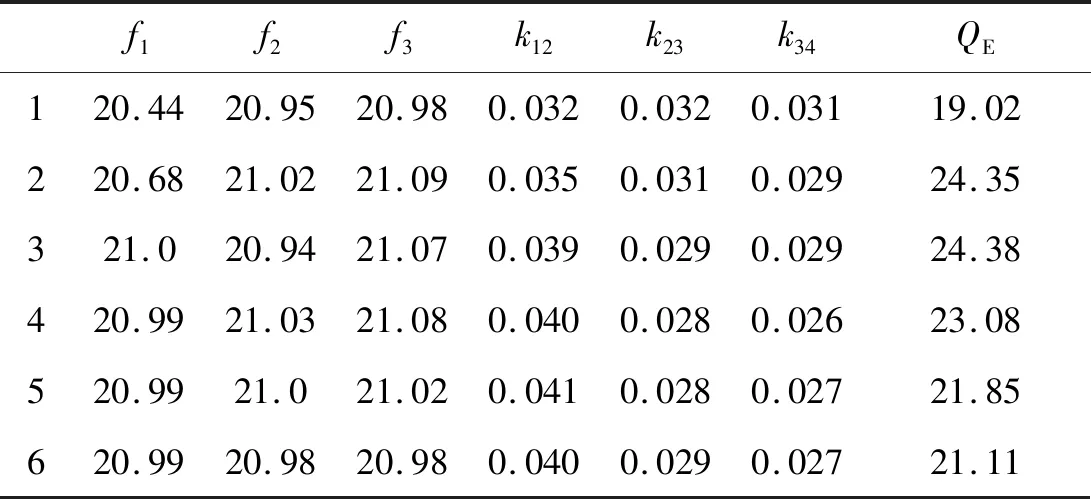
表4 電路模型參數變化過程

第6次仿真后，電路模型參數與式(8)、(9)所示的理論值已經非常接近，此時SIW濾波器的頻率響應如圖8所示。由圖可知，此時的濾波器性能已經十分良好，無需作進一步優化。

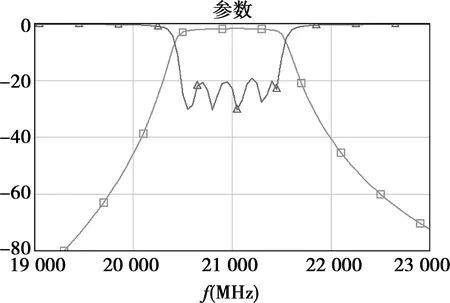
圖8 SIW濾波器仿真結果

4 結束語

本文采用快速設計方法設計了一個中心頻率為21 GHz、帶寬1 GHz的六階SIW濾波器。通過在AWR仿真軟件中建立SIW濾波器的等效電路模型，將耗時的全波仿真優化轉化快速的電路級優化，只需6次全波仿真即可得到性能良好的濾波器。