以探究為導向，構筑靈動、高效的課堂

張超

[摘? 要] 文章重點探究了一次函數的表達式與圖像之間的一一對應關系. 教學活動中讓學生經歷了“操作—猜想—探究—驗證”的過程，利用“描點法”繪制一次函數的圖像，引發了學生對“兩點法”刻畫一次函數圖像的思考.

[關鍵詞] 表達式;直線;一一對應

對教學目標以及所處教材體系的研究

蘇科版《義務教育課程標準試驗教科書·數學》（八年級上冊第6章6.5節）“一次函數圖像（第1課時）”是在學習了一次函數的概念、三種函數不同表示方法的基礎上，讓學生感受、探究一次函數的圖像，掌握用“描點法”來畫一次函數的圖像. 一次函數的圖像作為第一個函數圖形的研究，具有代表性. 結合課標，筆者對這節課教學目標的理解是：（1）一次函數的圖像是怎么形成的;（2）一次函數的圖像為什么是一條直線;（3）如何描繪出一次函數的圖像.

關于教學過程的研究

1. 情境引入

在太陽和月球引力的作用下，海水定時漲落的現象稱為海洋的潮汐，漲落的水位高低稱為潮位. 隨著時間t的變化，潮水的高度h也隨之發生變化. 假設海洋潮水高度h與時間t之間滿足這樣的函數關系式：

h=（t-2）2+1（0≤t≤5）.

問題1：你還有哪些不同的方法來表示h與t之間的函數關系？

問題2：表1中的兩個變量t，h的數值如何確定？

問題3：如何描繪該函數的圖像？

課堂回放 問題1回顧函數的三種不同表示方法;問題2引導學生通過t和h這兩個變量數值的對應，刻畫它們的函數關系;問題3利用直角坐標系把函數圖像問題轉化成點的坐標問題.

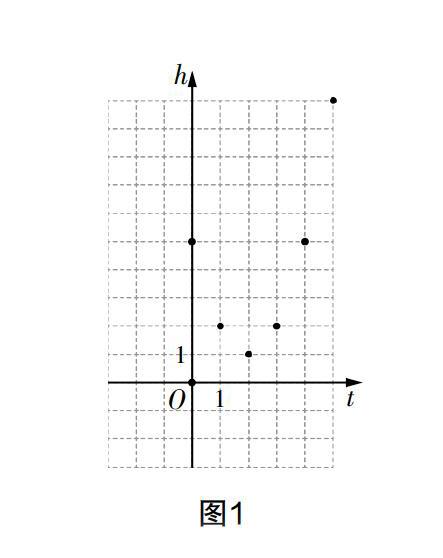
學生活動1 在平面直角坐標系中描繪出表1中關于兩個變量所形成的點.

課堂回放 師：函數圖像就是圖1中孤立的6個點嗎？說說你的見解.

生1：自變量t的取值范圍是0≤t≤5，t的取值除了整數外還可以取小數.

（學生動手嘗試自變量t是小數的點）

生2：函數的圖像中存在無數個點.

生3：（展示）無數個這樣的點“靠在一起”就形成了一條曲線（如圖2）.

（部分學生展開討論，表示質疑）

師：好，希望通過本節課的探究能幫助大家驗證猜想.

師：把一個函數的自變量x的值與函數y的對應值分別作為點的橫坐標和縱坐標，在直角坐標系中描出它的對應點，所有這些點組成的圖形叫這個函數的圖像.

師：回顧剛才畫函數圖像的過程，我們經歷了怎樣的步驟？

生（齊）：列表、描點、連線.

設計構想? 引入生活實例，體現數學源于生活. 通過對函數三種表示方法的認識，了解不同表示方法的聯系，為用描點法畫函數圖像做鋪墊. 選擇拋物線引入，目的是讓學生不陷入函數圖像是一條直線的定式中，也讓學生思考一次函數的圖像是否會像拋物線一樣是彎曲的.

2. 合作探究：一次函數y=2x+1的圖像及畫法

（1）小組合作，師生交流探究過程

師：列表應注意以下幾點.

①通常，我們所選取的點應具有完備性，x的值取正數、0、負數.

②列表的時候，自變量的數值從小到大排列.

③x與y有無數多組，兩邊用省略號表示，如表2.

課堂回放 師：在直角坐標系中描繪出這些點，它們在位置上有什么關系？（提示學生動用直尺去比對）

生（齊）：在一條直線上.

師：你還能找到哪些點？

生4：（0.5，2），（1.5，4），（2.5，6）.

生5：自變量也可以是負數，如（-0.5，0），（-1.5，-2），（-2.5，-4）.

師：請大家描繪出剛剛兩位同學所找的點，再觀察這些點的位置.

生6：這些點仍然在同一條直線上.

師：剛才大家通過觀察（圖3），發現這些點位置上的特殊關系，能否保證函數圖像所有的點都具有這樣的特征？

（學生小聲議論，有一些遲疑）

師：如果把自變量x在0到1之間10等分，橫坐標分別取0.1，0.2，…，0.9，描繪出這些點（如圖4），觀察這些點的特征.

（學生通過幾何直觀，發現這些點“靠”在一起形成了一條直線）

師：擴大橫軸上的單位長度，如圖5，再觀察這些點的位置.

生（齊）：這些點又分開了.

師：能使圖像中的點“靠”得更近點嗎？

生7：0～1之間可以取更多的點，讓點密集起來.

師：能否具體點？

生8：可以把自變量0～0.1，0.1～0.2，…，0.9～1再分別10等分.

師：好，看圖6.

（學生的觀察是點又形成了線）

（2）初步小結：深化理解

課堂回放 師：自變量在0～1之間還可以無數次等分下去，形成無數個點，它們會“靠”在一起形成一條線. 那么，1～2，2～3…同樣如此.

共同歸納：—次函數y=2x+1的圖像是一條直線（如圖7）.

師：在這條直線上任意取點，如（-2，-3），（1，3），橫坐標與縱坐標滿足什么關系？

生9：橫坐標與縱坐標的數值滿足一次函數的表達式.

師：滿足一次函數表達式的x和y轉化為坐標是否也在函數圖像上呢？

師生總結：函數的圖像與表達式之間是一一對應關系（如圖8）.

3. 深入探究：優化一次函數圖像的畫法

學生活動2 已知一次函數y=-3x+2.

（1）試判斷（4，-10），（-3，8），（0，2）三點是否在函數y=-3x+2的圖像上;

（2）若（3，a），（b，7）兩點在函數圖像上，求a，b的值;

（學生根據函數的表達式與圖像之間的關系，迅速作答）

（3）畫出一次函數y=-3x+2的圖像（限定時間1分鐘）

（1分鐘后，有部分同學舉手示意）

課堂回放 師：你描了哪些點？

生10：（0，2）和（1，-1）兩個點.

師：說說你的想法.

生10：兩點確定一條直線.

師：能否舉例驗證滿足函數表達式的點都在如圖9所示的直線上？

師生互動：（借助幾何畫板）逐個描出學生列舉出的點的坐標，如（-1，5），（-0.5，3.5），（0.5，0.5），（1.5，-2.5），（2，-4），如圖10，得出滿足函數表達式的點都在同一條直線上.

師生共同總結：滿足一次函數表達式的兩個點就可以確定它的圖像（“兩點法”）.

學生活動3 快速畫出一次函數y=x+1的圖像.

課堂回放 師：哪些位置上的點的坐標比較容易確定？為什么？

生11：兩個坐標軸上的點的坐標容易確定，因為x軸上的點的縱坐標為0，y軸上的點的橫坐標為0（板書如表3）.

[x 0 -3 y 1 0 ][表3]

師：根據這兩個點的坐標，畫出函數y=x+1的圖像.

師：對于一次函數的一般形式y=kx+b（k≠0），如何快速地找出兩個點的坐標從而畫出函數圖像？

生12：板書如表4.

[x 0 - y b 0 ][表4]

4. 回顧思考：知識的梳理及小結

（1）對于函數h=（t-2）2+1（0≤t≤5）的圖像，能否找到方法驗證猜想？

（2）一次函數的圖像是直線，對此你有哪些認知？

（3）一次函數的表達式與它的圖像有何關系？

（4）怎樣畫一次函數的圖像？

課堂回放 學生回答，教師補充點評.

教學思考

1. 深入探究，注重數學理解

張奠宙先生把數學教學認為是數學教育形態的教學[1]. 數學教育形態的本質是教師創造數學理解. 數學理解是建立在循序漸進的認知過程基礎上的，根據數學的思想與方法、知識與技能，探究數學知識的發生與發展過程. 對于教材中的概念、定理、法則，進行課堂教學時，需要教師對教學內容進行符合實際教學情況的改造與演繹. 所以，教師在教學中的真正價值體現，在于對數學理解的把握.

筆者就這節課的理解，體現在兩個層面：一是如何引導學生畫函數圖像. 本課的情境引入是拋物線的研究，滲透畫函數圖像的三個步驟. 對于一次函數圖像的畫法，則采用類比探究的方式. 過程中，表格中自變量x如何選取、點的坐標如何確定、由描繪的一個個孤立的點如何確定函數的圖像，是本節課創造數學理解的關鍵. 二是如何驗證一次函數的圖像是一條直線. 隨著課堂探究的深入，學生經歷了感受（列表、描點），形成了感知（判斷一次函數的圖像是一條直線）. 當然，學生如何形成感悟，成為本節課數學理解的核心. 探究過程中，筆者引導學生仍從“點”出發，強化函數的圖像是由無數個點形成的，采用了從“局部”到“整體”的思維方式. 例如圖5中，自變量0～1之間取10等分，觀察這些點的位置. 通過控制直角坐標系的單位長度，可以進一步把自變量在0～0.1，0.1～0.2，…，0.9～1之間再各自10等分，讓更多滿足函數表達式的點“密布”. 這樣的方式能讓學生通過圖形感知理解——這些無數個“密布”的點“靠”在一起，就“連”成了一條直線.

2. 鼓勵質疑，促進課堂動態生成

“學貴有疑，疑而出新. ”實際教學中，教師對于學生的質疑要適時鼓勵，要給予他們創造性思考的信心. 例如，本節課“問題情境”中的二次函數圖像，描點后連線（如圖2），部分同學提出質疑：圖像為何是曲線而不是折線？學生在沒有任何認知的前提下，大膽地提出了他們的想法. 此時除給予鼓勵外，還要抓住學生課堂中生成的問題，設置懸念，激發學生的探究興趣[2]，同時為確定一次函數的圖像做鋪墊. 探究得出一次函數的圖像是一條直線后，再次回到“問題情境”，確定二次函數圖像的問題，根據一次函數探究的認知理論，學生較易找出驗證的方法，這完全立足于學生的最近發展區.

3. 立足于教學體系，遵循邏輯關系

學習完一次函數的概念及表達式后，學生對函數的理解還較為抽象，那如何讓函數更為具體地表示，強化學生對函數的認知與理解呢？函數圖像的引入，是通過圖形來刻畫抽象的表達式，做到了“數”與“形”的對應. 在教學環節設計的過程中，教學內容的落腳點首先是感受畫函數圖像的方法步驟，然后通過描出點的位置猜想函數圖像，自然螺旋上升到函數圖像的驗證. 探究過程中對于函數圖像的感受、猜想、驗證，最終都是讓學生能夠理解性地熟練刻畫一次函數的圖像. 基于研究性的數學教學，以靈動高效的課堂作為支撐，既能滿足學生“知其然”，更追求“知其所以然”.

參考文獻：

[1]張奠宙. 教育數學是具有教育形態的數學[J]. 數學教育學報，2005，14（3）：1-4.

[2]黃文光，酈興江. 理解“三個理解”? ? 凸顯數學思想[J]. 中學數學，2015（2）：55-56.