基于FLUENT的擺桿式明渠測流特性數值模擬

周義仁，石先德，張 茜

(太原理工大學水利科學與工程學院，太原 030024)

灌區精準量水是提高農業用水利用率的基礎所在[1]，本文針對灌區量水過程中存在的測流精度低、水頭損失大等問題提出了一種新型量水裝置----擺桿式明渠測流裝置，其工作原理需建立擺桿擺動角度和渠道流量之間關系進行測流，探究該裝置在不同類型渠道和測流擺桿下的測流特性具有重要意義。隨著數值模擬技術的發展，計算流體力學所能計算的領域越來越多[2]，通過數值模擬方法建立數學模型解決實際工程問題具有投入少、研究周期短、可調參數多等優點。FLUENT是目前應用最為廣泛的計算流體力學軟件，其計算方法及后處理功能十分先進[3]。擺桿式明渠測流裝置進行測流任務時，測流擺桿由于水流沖擊而擺動，是屬于固體邊界在流域中產生的被動運動，在FLUENT中，動網格模型可以用來模擬由于流域邊界運動引起流域形狀隨時間變化的流動情況，也可以用來模擬由于流場改變而導致固體邊界發生被動運動情況[4,5]。利用FLUENT軟件對擺桿式明渠測流裝置測流特性進行研究，可以提高該裝置的測流精度及適用性。

1 擺桿式明渠測流裝置簡介

擺桿式明渠測流裝置機械結構如圖1所示。

1-渠道邊坡；2-調平旋鈕；3-可伸縮不銹鋼支架；4-超聲波探頭；5-液晶顯示器；6-供電及數據處理模塊；7-水平儀；8-角度傳感器；9-測流擺桿圖1 擺桿式明渠測流裝置

圓柱形擺桿放置于流動的水中時受到渠道水流阻力和升力作用，會沿水流方向擺動，通過建立渠道流量和擺桿擺動角度之間的關系，測得擺桿旋轉角度便可以得知渠道瞬時流量。

2 數值模擬研究

2.1 計算模型及控制方程

計算采用VOF自由液面模型，對于水氣兩相流動，VOF模型對其進行描述時，先定義函數qw(x,y,z,t)和qa(x,y,z,t)，它們分別表示水與空氣在某一時刻的某一單元格內的體積分數。而在每一個單元格內[6]：

qw+qa=1

(1)

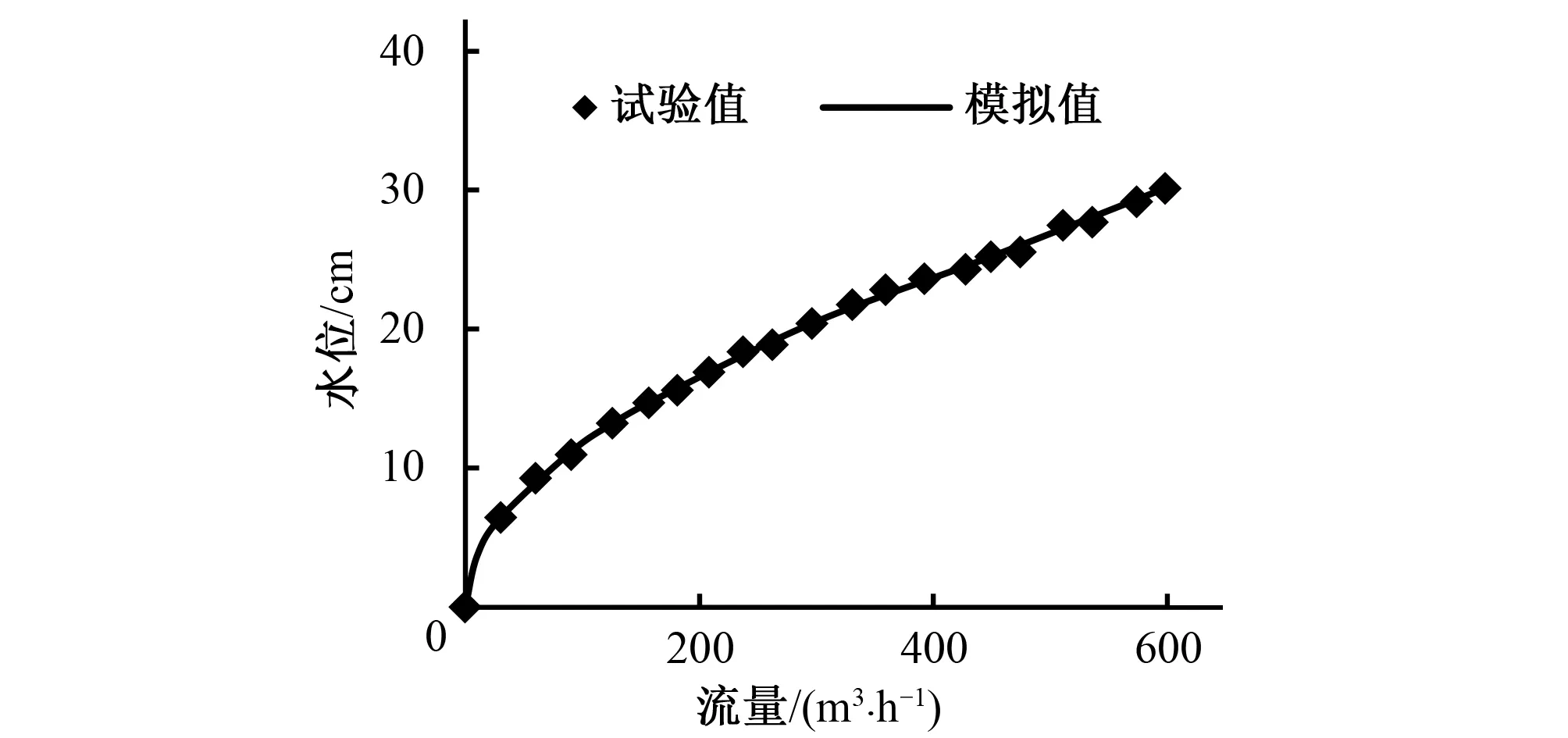
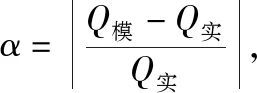
通過公式(1)能夠得到，當qw=1時，表示在該單元格內水的體積分數為1，也就是這個單元內充滿了水；反之，qa=1時，則表示這個單元內全都是空氣；若0

(2)

式中：t為時間；ui為速度分量；xi為坐標分量。

湍流模型選用Realizablek-ε模型，連續性方程、動量方程、湍流動能k方程、湍流耗散率ε方程如下所示[8]：

(3)

(4)

Gk+Gb-ρε-Ym+Sk

(5)

(6)

2.2 幾何建模及網格劃分

本文模擬及試驗所用渠道為D50型U形渠道，其主要參數為：渠深0.5 m，渠道底弧半徑0.25 m，底弧圓心角163°，渠道傾角8.5°，渠頂寬度0.58 m，渠道底坡為1/1 000。為了充分模擬U形渠道水流流態并盡量減少計算機模擬時間，渠道長度設為4 m，入口處1 m設置長方體穩流池，確保水流從入口處平穩過渡到U形渠道中。設備放置于U形渠道中央，距出口2 m位置，取擺桿頂端圓心為坐標原點，水流方向為Z軸正方向，豎直向上為Y軸正方向，順水流方向左岸為X軸正方向，如圖2所示。

圖2 坐標軸示意圖

結構化網格與非結構化網格聯合進行求解，可以很好地解決計算緩慢以及網格質量差等問題，使得模擬更加精準和高效[9,10]。計算模型在最大尺度以及最小尺度之間存在較大差異(渠道長達4 m，測流擺桿直徑為5 mm)，所以在擺桿上下游0.5 m以內采用非結構化網格，在擺桿運動范圍之外采取結構化網格。設置全局網格最大尺寸為4 cm，在擺桿周圍進行非結構化網格劃分，并對擺桿進行局部加密處理，擺桿表面最大網格尺寸為1 mm，網格總數約為36萬個，網格劃分如圖3所示。

圖3 網格劃分示意圖

2.3 邊界條件及求解方法

為了更加精確的模擬渠道水流流動對擺桿式明渠測流精度的影響，上游設置進口為速度入口(VELOCITY-INLET)，利用平均流速來控制渠道瞬時流量大小；下游出口設置為壓力出口(PRESSURE-OUTLET)；渠道頂部設為壓力進口(PRESSURE-INLET)，受到大氣壓強作用，頂部參考壓強為101 kPa；擺桿以及渠道側面全部設為無滑移固體邊壁，渠道壁面為不銹鋼材質，設置壁面粗糙度高度為0 cm，粗糙度常數為0.5。整個計算域中最開始時充滿了空氣，通過VOF方法進行迭代，自動生成水氣交界面。

本文主要采用有限體積法進行計算，主要步驟是進行計算區域劃分后，進行區域的離散化與控制方程的離散，計算區域的離散化實質上便是上述所提到的網格劃分。控制方程的離散化可以利用如下所示的通用形式表示[11]：

(7)

式中：ρ為流體密度；u為液體流速；t為時間；φ為廣義變量，可以為速度、溫度或者濃度等一些待求物理量；Γ是相應于φ的廣義擴散項；Sk是廣義源項。

建立了可以進行計算的代數方程組之后，需要對各個未知量的求解順序以及方式進行特殊處理，對于瞬態計算，采用PISO算法比SIMPLE或者SIMPLEC算法更加合適。

2.4 動網格設定

在FLUENT中動網格更新方法主要有3種，包括彈簧近似光滑模型(Spring-based Smoothing)、動態分層模型(Dynamic Layering)以及局部網格重構模型(Local Remeshing)[12]。本文主要采用彈簧光順與局部網格重構相結合進行計算。

動網格流場控制模型中，計算區域是變化的，其守恒方程為[13]：

(8)

FLUENT中6DOF(六自由度)模型主要是用于模擬計算域中的剛體構件受到流體的作用之后運動的軌跡及狀態，通過模擬流體的運動對剛體產生的作用力，來推算剛體的運動軌跡。其中剛體的質量、位移、旋轉以及轉動慣量可以通過UDF(用戶自定義函數)來進行編寫錄入[14]。

本文主要研究3種不同材質的測流擺桿在D50型U形渠道下的測流特性，不同材質的擺桿參數如表1所示。

3 結果分析

3.1 水面線分析

對明渠進行三維數值模擬時，水面線是一項基本研究對象，通過試驗與模擬結果的比較，可以驗證數值模擬的可行性。

表1 不同材質測流擺桿參數

對不同流量下D50型U形渠道水流進行模擬可以得到測流裝置下方(Z=0 m)水位隨流量變化圖，如圖4所示。

圖4 水位與流量關系圖

當渠道瞬時流量為300 m3/h時，采用鋁材測流擺桿，t=0 s時開始從入口注水，渠道水流從入口到出口水面線隨時間變化瞬態圖如圖5所示，圖中藍色區域為空氣，紅色區域為水流，紅藍相間區域為水氣交界面，白色區域為擺桿。觀察圖5可以發現，隨著入口處水流不斷涌入渠道，渠道中水位逐漸上升，當t=6.87 s以后，水位趨于平緩。穩流池與渠道相接處水面略有壅高，這是由于穩流池出口截面較小，水流撞擊壁面后造成水位上升。測流設備上下游1 m水流平緩，在渠道出口處水位有所下降。由圖4與圖5可以發現，利用數值模擬對U形渠道進行仿真模擬得到的渠道水位與試驗結果相近，所以利用VOF方法以及Realizablek-ε湍流模型對渠道水流進行數值模擬可以得到與實際相符的結果。

圖5 300 m3/h流量下渠道沿程水面線變化圖

3.2 流速分布

為了解U形渠道過水斷面流速變化特征，對測流設備下方(Z=0 m)測流斷面進行流速分析，如圖6所示為不同流量下，渠道過水斷面沿水流方向(Z軸正方向)水流流速分布云圖。

由圖6可以發現，在底坡為1/1 000的D50型U形渠道中，隨著渠道內流量的增加，過水斷面面積增大，水位逐漸升高，水流流速逐漸增大，當流量為150 m3/h時，最大流速為0.96 m/s，當流量為600 m3/h時，最大流速達到1.37 m/s。對于渠道斷面沿水流方向的流速分布而言，在靠近渠道邊壁的流速急劇下降，在渠道邊壁區域接近于0 m/s，其最大流速位于水面下方，在氣液交界面處，流速較緩，這與渠道實際流速分布規律相吻合。

3.3 動網格變化分析

對于動網格的計算方法，本文主要采用彈簧光順與局部網格重構相結合進行計算。彈簧光順將網格節點視為可變形的彈簧，固體邊界發生位置變化時，將會擠壓或者拉伸網格，通過求解彈簧的應力平衡方程得到新網格的節點位置，但是其只能處理網格微小變形的情況，當網格變形較大時，則需要利用局部網格重構技術。針對網格尺寸以及畸變率，當網格出現較大程度的變形時，將會對該區域的網格進行網格重構，通過守恒定律以及插值映射從舊網格中得到物理量的大小。如圖7所示，以不銹鋼材質擺桿在不同流量的水流作用下產生網格重構的變化為例，對動網格變化進行分析。圖7藍色區域為空氣，紅色區域為水流，紅藍相間區域為水氣交界面。

圖6 不同流量下斷面流速分布云圖

圖7 不銹鋼材質擺桿局部網格變化

由圖7可以發現，當擺桿受到水流作用向下游擺動時，擺桿周圍的網格發生變形，下游網格受到擺桿擠壓，體積變小，而擺桿上游位置的網格體積增大。隨著流量的增大，擺桿擺動的角度隨之增大，動網格更新的區域也隨之增大，且之前擺桿經過的區域網格變得更加密集。在整個迭代計算過程中，網格體積始終沒有出現負體積。通過模擬研究發現，鋁材以及有機玻璃兩種材質的測流擺桿與圖7中不銹鋼材質擺桿周圍網格變化規律相似，說明采用FLUENT中6DOF動網格模型模擬擺桿式測流裝置測流特性是可行的。

3.4 測流公式及精度分析

擺桿式明渠測流裝置測得流量Q與以下因素有關：水的密度 、重力加速度g、測流擺桿密度 、測流擺桿長度L、測流擺桿直徑D、測流擺桿被水推動的水平位移d(d=Lsinθ)、水中泥沙濃度S、水動力黏滯系數v、渠道糙率n以及渠道底坡i。擺桿式明渠測流裝置的測流計算公式可以通過量綱分析法推導得到。選取d，g，ρ桿3個相互獨立的量作為研究基本物理量，最終可以得到以下測流公式：

(9)

(10)

Q=Ksin2.5θ

(11)

對D50型U形渠道下不同材質的測流擺桿測流特性進行數值模擬，得到3種材質擺桿在不同流量下相應擺動角度，利用線性擬合得到式(11)中系數K的大小，便得到了擺桿式明渠測流裝置在該渠道下的測流公式，如表2所示。

表2 不同材質測流擺桿測流公式

圖8為模擬值與試驗值對比圖，主坐標軸反映了不同材質的測流擺桿sin2.5θ與渠道流量Q之間的關系，次坐標軸反映了利用表2算得流量與實際流量之間的相對誤差。由圖8可以發現，不同材質的測流擺桿在U形渠道下，渠道流量Q與擺桿擺動角度sin2.5θ之間成正比例函數關系，模擬值與試驗值變化一致。利用測流公式得到渠道流量與真實流量之間相對誤差α較小，其中不銹鋼材質的測流擺桿測得流量最大相對誤差為5.33%，平均相對誤差為2.5%；鋁材測流擺桿測得流量最大相對誤差為5.55%，平均相對誤差為1.87%；有機玻璃材質測流擺桿測得流量最大相對誤差為5.26%，平均相對誤差為2.22%。

4 結 語

利用FLUENT對擺桿式明渠測流裝置在底坡為1/1 000的D50型U形渠道下測流特性進行數值模擬研究，通過數值模擬以及試驗數據對比分析得到以下結論。

圖8 不同材質擺桿流量與角度關系圖

(1)利用FLUENT中VOF模型與Realizablek-ε湍流模型對D50型U形渠道下水流特性進行模擬研究是可行的，模擬渠道沿程水面線與試驗相符。渠道過水斷面上流速分布規律為：在靠近渠道邊壁的區域水流流速急劇下降，在邊壁旁趨近于零，而水流最大流速并不是位于水面位置，而是在水面下方的位置，這也與國內外其他學者研究結論一致。

(2)利用6DOF動網格模型對測流擺桿擺動特性進行模擬是可行的，通過水流與擺桿之間的耦合計算可以得到擺桿的擺動角度與渠道流量大小之間的變化規律，隨著渠道內瞬時流量的增大，擺桿擺動的角度也逐漸增大，擺桿周圍非結構化網格產生重構。

(3)利用數值模擬對擺桿式測流裝置測流精度進行研究，發現量綱分析得到的測流公式Q=Ksin2.5θ中系數K大小隨著擺桿密度的減小而減小，測得流量與實際流量之間平均相對誤差小于3%，可以滿足明渠測流精度要求。

本文對擺桿式明渠測流裝置測流特性進行數值模擬研究，模擬結果與實際情況一致，充分驗證了該測流裝置的可行性，對提高該裝置測流精度有重要意義，為灌區精準量水的發展提供了新思路。