基于波傳播系數構建填實爆炸下花崗巖中運動及變形場*

盧 強，王占江，朱玉榮，丁 洋，郭志昀

（1. 西北核技術研究院，陜西 西安 710024；2. 西北核技術研究院強動載與效應重點實驗室，陜西 西安 710024）

波傳播系數法的研究始于Kolsky[1]及Hunter[2]的工作，他們采用傅里葉變換法研究了線黏彈性桿中的一維波傳播問題，由桿衰減系數和波數（或波速）表示線黏彈性材料的復模量，并以頻率衰減因子和波數作為波傳播分析的參數。自此之后，眾多學者對波傳播系數分析方法在桿中的應用進行了研究。Zhao 等[3-4]給出了考慮三維效應的無限長桿中縱波的通解，并進行了一些材料力學行為動態測試實驗驗證，結果表明利用考慮三維效應后的波傳播系數去修正實驗結果能夠提高分析精度。Bacon 等[5-8]將前人的研究成果加以整理和完善，利用入射波和反射波的分離技術，提出了波傳播系數的一點應變測試方法。Casem 等[9]及Mousavi 等[10-11]將波傳播系數法在低密度泡沫材料和聚丙烯材料動態力學性能研究中進行了初步的嘗試。Benatar 等[12]簡化了Pochhammer-Chree 頻率方程[13]，采用 ?12 mm 和 ?6.4 mm 的PMMA（polymethyl methacrylate）桿進行了一維波傳播實驗，修正了黏彈性桿中應力波傳播的幾何效應，并把兩種桿徑下實測的隨頻率變化的相速曲線、衰減曲線進行了對比，結果表明黏彈性桿理論可以在較寬的頻率范圍內確定材料的黏彈性特性。Ahonsi 等[14]采用鋼球撞擊作為桿中產生應力波的源，理論分析中采用了一個彈性元件和一個Maxwell 元件并聯的模型（標準線性固體模型）對傳播系數進行了分析。Butt 等[15-16]采用一個彈性元件和兩個Maxwell 元件并聯的模型（5 參數模型）分析了PMMA 桿中的傳播系數，并反演了此模型對應的材料參數。Fan 等[17]采用一個非線性彈性元件和一個Maxwell 元件并聯的模型分析了混凝土材料的黏彈性特性，給出了混凝土的衰減系數和波數，通過參數識別給出了混凝土材料非線性本構參數。Othman[18]采用尼龍材料作為輸入輸出桿對泡沫鋁材料進行了SHPB 測試，施加在泡沫鋁兩個端面上的載荷由尼龍桿的傳播系數校正（標準線性固體模型），指出若按彈性假設處理軟材料的SHPB 實驗數據，在小應變、高應變率時會引入不可忽略的誤差。

上述研究均為桿中黏彈性波傳播相關的內容，目的是為結合黏彈性霍普金森壓桿實驗技術來研究低阻抗材料的動態力學性能。本文中從黏彈性球面波的頻率方程出發，利用花崗巖中有限個實測的球面波徑向粒子速度頻譜信息，給出球面波傳播系數的求解方法，分析花崗巖球面波傳播系數的變化，提出一種構建地下爆炸介質運動及變形場的方法。

1 黏彈性球面波的頻率方程

根據黏彈性球面波的分析，地下爆炸自由場徑向粒子速度和震源函數在頻域內滿足如下關系[19-20]：

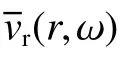
任意兩個位置 r1和 r2處 粒子速度的理論頻譜比 HT(r1,r2,ω)可寫為：

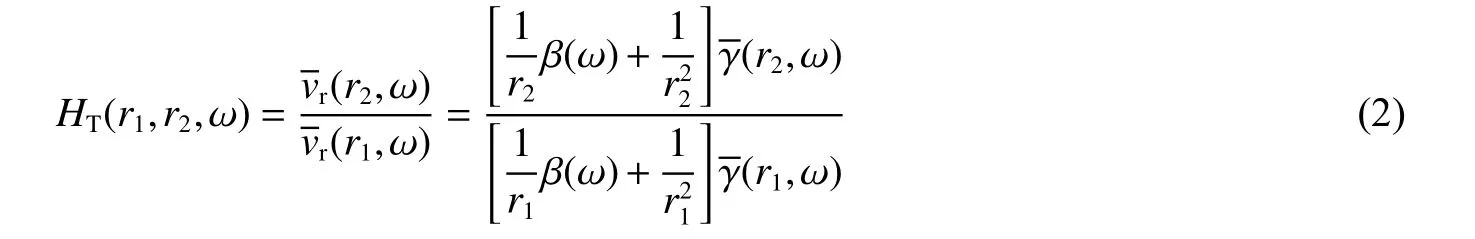
因此理論頻譜比 HT(r1,r2,ω)可以寫為：

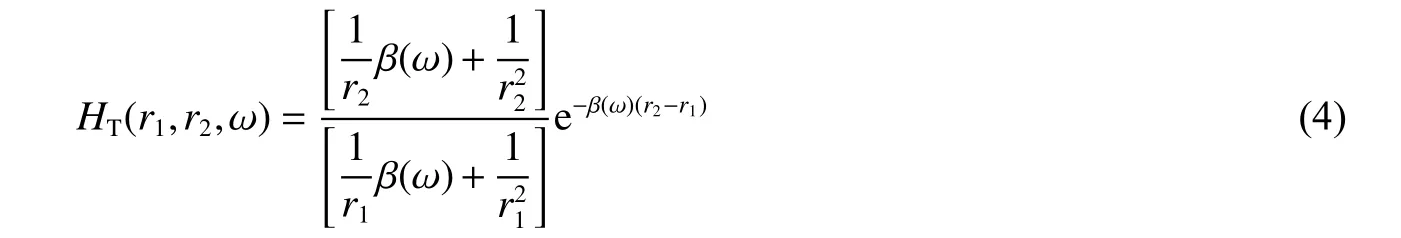
由公式（4）可以看出，理論頻譜比 HT(r1,r2,ω)是 爆心距參數 r1、 r2和 波傳播系數 β(ω) 的 函數。 β (ω)是控制波在傳播過程中形狀改變的重要參數，客觀上反映介質的黏性對波傳播演化的影響。若爆心距 r1、r2處 的徑向粒子速度已知，則可通過公式（4）求解出波傳播系數β (ω)。

2 球面波傳播系數的求解方法

利用球面波實驗技術和圓環型粒子速度測試技術，可以得到有限個不同爆心距位置處的徑向粒子速度[21]。利用這些測得的粒子速度中的任意兩個，可以給出相應的實驗頻譜比 HE(r1,r2,ω)，即：

式中： ?t 為徑向粒子速度的采樣時間間隔， M 和 N 分別為 r1和 r2處粒子速度的有效采樣點數。

若假設巖土是黏彈性介質，則理論頻譜比與實驗頻譜比一致，通過公式（4）定義函數g (r1,r2,β(ω))：

從公式（6）可以看出，僅有 β(ω)是需要求解的。利用Newton 迭代法，有：

式中： βn(ω)的 下標表示第 n次迭代。

數值迭代求解公式（7）的關鍵是確定波傳播系數的初值 β0(ω)， 即要分別確定衰減因子初值 α0(ω)和波數 k0(ω)。把公式（4）展開，可得到：

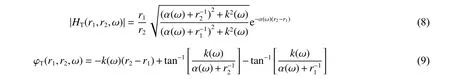
式中： |HT(r1,r2,ω)|和 φT(r1,r2,ω)分 別為 HT(r1,r2,ω)的模和輻角。

把公式（9）進行簡化，忽略公式右邊的兩項，得到波數的近似值作為其初值，即：

再把 k0(ω)代 入公式（8），即可求出衰減因子初值 α0(ω)，即：

由此給出波傳播系數的初值 β0(ω)=α0(ω)+k0(ω)i，按照公式（7）經過有限次迭代即可給出收斂的波傳播系數 β(ω)。

3 填實爆炸下花崗巖中傳播系數的實例與討論

本文中以王占江等[21]在0.125 g TNT 填實爆炸下實測的花崗巖中徑向粒子速度為基礎（如圖1 所示），按照前述方法對花崗巖的波傳播系數進行了分析。由于爆心距10 mm 處粒子速度計在沖擊下損壞、爆心距大于60 mm 的粒子速度計受樣品邊界反射波的影響，這些傳感器獲得的粒子速度信號相對不夠完整，因此在進行波傳播系數分析時不予以考慮。

利用爆心距15～50 mm 處的粒子速度頻譜，依次選取兩個相鄰測點來計算相應的實驗頻譜比HE(r1,r2,ω) 。 圖2 給出了 r1= 15 mm、 r2= 20 mm 和 r1= 40 mm、 r2= 50 mm 時的輻角曲線 φE(r1,r2,ω)，可以看出，當 r1= 15 mm、 r2= 20 mm 時， ω≈ 1.5×107rad/s（對應頻率 f≈2.38 MHz）時波數曲線開始出現突然增大或減小，這是違背物理規律的。同樣，當 r1= 40 mm、 r2= 50 mm 時， φE(r1,r2,ω)出現類似的現象。本文中把這些開始出現違背物理規律的頻率點視為波傳播系數有效頻段的上限 ωmax。因此，由實測數據計算得到的衰減因子 α(ω)和 波數 k (ω)只在有限頻段內是可信的。

圖3～4 分別給出了相鄰測點之間區域內花崗巖傳播系數中的衰減因子 α(ω)和 波數k (ω)，圖5 給出了和波數曲線對應的相速度曲線。從圖3～4 可以看出，測點距爆心越遠，傳播系數有效頻段的上限ωmax越低。這是因為波傳播過程中，由于介質耗散和幾何發散的影響，粒子速度的高頻成分衰減快，導致遠區的高頻信息較弱，高頻信號成分的信噪比較低，從而造成波傳播系數有效頻段上限 ωmax的降低。

另外，由于樣品尺寸小，導致信號低頻成分未能充分發展即受到樣品邊界反射波的影響，因此衰減因子 α(ω)和 波數 k(ω)的低頻結果是不可信的。按照王占江等[22]的結果，本文中使用的花崗巖用超聲測得的波速為2 700 m/s。把圖5 中相速度低于2 700 m/s 的部分進行標示，可以近似對衰減因子 α(ω)和波數k(ω)有 效頻段的下限 ωmin進行估計，即本文中給出的在幾十kHz 以下的波傳播系數是不可信的。

從圖5 給出的相速度曲線還可以看出，在有效頻段內，相速度曲線有一個平臺值，距爆心越遠，這個平臺值越小。按照前述的黏彈性假設，理論上獲得的波傳播系數應具有一致性，但從本文中處理的結果看，在15～50 mm 區域所處的應力條件下花崗巖沒有體現出理想的黏彈性行為。利用盧強等[23]給出的利用球面波徑向粒子速度波形反推有機玻璃力學參數的方法，圖6 給出了0.125 g TNT 填實爆炸下花崗巖中等效應力峰值 τmax隨爆心距 r 的變化。可以看出，在爆心距35 mm 處的等效應力峰值 τmax約為158 MPa，略大于花崗巖的單軸壓縮強度154 MPa[22]，可近似認為0.125 g TNT 填實爆炸下，花崗巖彈性區的半徑約為35 mm。因此，本文中所處理的區域中，爆心距15～35 mm 范圍屬于塑性區，35～50 mm 區域屬于黏彈性區。從黏彈性區計算得到的波傳播系數看，即使是低幅值的弱波，花崗巖表現出來的也不是理想的黏彈性力學行為。

圖 1 0.125 g TNT 填實爆炸下花崗巖中實測的徑向粒子速度[21]Fig. 1 Measured radial particle velocities in granite under the tamped explosion of 0.125 g TNT

圖 2 花崗巖中實驗頻譜比 HE(r1,r2,ω)的輻角 φE(r1,r2,ω)隨 ω的變化Fig. 2 Argument φ E(r1,r2,ω) of the experimental spectrum ratio HE(r1,r2,ω) in granite vs the circular frequency ω

圖 3 利用花崗巖中相鄰測點數據計算的衰減因子α(ω)Fig. 3 Attenuation factor α( ω) calculated from the data of adjacent measuring points in granite

圖 4 利用花崗巖中相鄰測點數據計算的波數k(ω)Fig. 4 Wave number k (ω) calculated from the data of adjacent measuring points in granite

4 利用有限個實測粒子速度構建花崗巖中運動及變形場

4.1 局部黏彈性等效方法

前面按照黏彈性假設計算了相鄰測點之間花崗巖的波傳播系數，衰減因子α (ω)和 波數 k (ω)基本反映出了爆炸應力波從近區的高壓狀態演化到相對遠區的低壓狀態時花崗巖對波吸收和彌散的頻率相關性。下面對上述不同區域的波傳播系數作進一步的應用分析。

如圖7 所示，爆炸應力波由 r1處傳播至 r2，由兩個位置處粒子速度的頻譜比，可以求得一個局部黏彈性等效的波傳播系數 βvisco(r1,r2,ω)。假設局部黏彈性等效成立，由公式（2）、（4）可以得到 r1和 r2之間任意位置 r處的頻譜比，即：

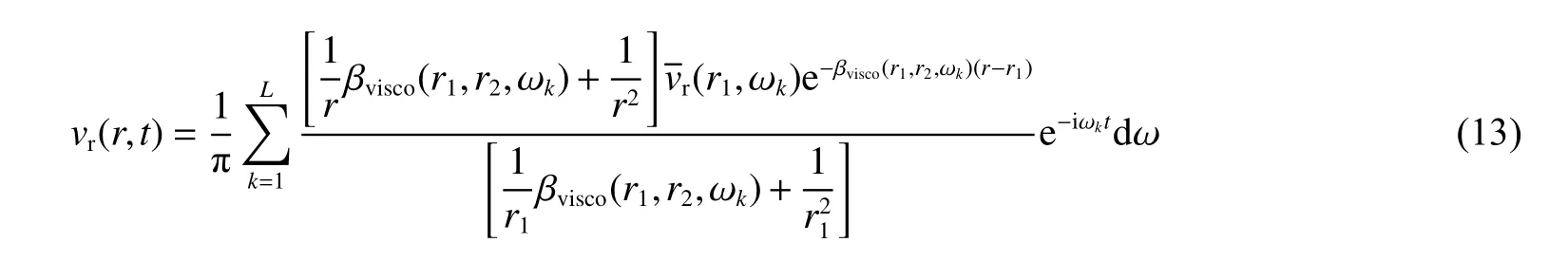
圖 5 利用花崗巖中相鄰測點數據計算的相速度c(ω)Fig. 5 Phase velocity c (ω) calculated from the data of adjacent measuring points in granite

圖 6 0.125 g TNT 填實爆炸下花崗巖中等效應力峰值τmax隨爆心距 r的變化Fig. 6 Peak value of the equivalent stress τ max vs. r under the tamped explosion of 0.125 g TNT in granite

圖 7 局部黏彈性等效下粒子速度場的構建方法Fig. 7 Method for constructing particle velocity field under local viscoelastic equivalence

若以局部理想彈性等效處理，即忽略 β(r1,r2,ωk) 中 的頻率衰減因子 α (r1,r2,ωk) ，并把 β (r1,r2,ωk)中的波數k(r1,r2,ωk)以 爆炸應力波由 r1處 傳播至 r2處 的平均波速 c (r1,r2)表示：

局部彈性等效條件下， r1和 r2之間任意位置 r 處的粒子速度 vr(r,t)可寫為：

圖8 通過花崗巖 r1= 15 mm 和 r2=25 mm 處粒子速度計算的局部黏彈性等效波傳播系數βvisco(r1,r2,ω)以及局部彈性等效波傳播系數βelastic(r1,r2,ω)，分別計算了r=20 mm 和25 mm 處的粒子速度。可以看出，采用局部黏彈性等效方法計算的粒子速度在r1和r2區域兩端精度很高，中間位置(r=20 mm)處計算的粒子速度在峰值以及形狀方面均和實驗結果保持較高的相似性。以局部彈性等效方法計算的r=20，25 mm 處的粒子速度同實驗結果的差異較大，無論是粒子速度峰值還是波形形狀均不能很好地反映出當地粒子速度波形本來的特點。這里強調，0.125 g TNT填實爆炸下花崗巖中15、25 mm 處還是塑性區的范圍，但從基于局部黏彈性等效方法計算 r1和 r2之間區域的粒子速度看，其精度遠高于局部彈性等效方法，這也說明雖然局部黏彈性等效的波傳播系數是基于黏彈性理論給出的結果，但在塑性區應用時仍有較好的表現。

圖 8 局部黏彈性等效和局部彈性等效方法計算的粒子速度波形的比較Fig. 8 Comparison of particle velocity waveforms calculated by local viscoelastic with that by elastic equivalence method

4.2 花崗巖中變形場的分析

采用局部黏彈性等效方法，利用相鄰測點獲得的徑向粒子速度可給出相鄰測點區域內任意位置的粒子速度，即給出粒子速度的時間-空間場 vr(r,t)， 如圖9 所示。對粒子速度場 vr(r,t)積分可得粒子位移場ur(r,t)， 如圖10 所示。由位移場 ur(r,t)可得徑向和切向應變（率）場：

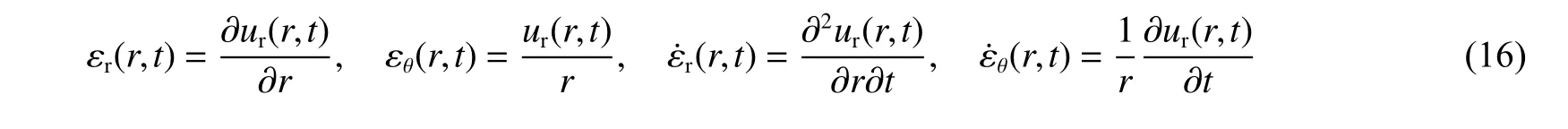
圖 9 采用局部黏彈性等效方法構建的粒子速度場vr(r,t)Fig. 9 Particle velocity field vr( r,t) constructed by local viscoelastic equivalence method

圖 10 采用局部黏彈性等效方法構建的粒子速度場ur(r,t)Fig. 10 Particle displacement field u r(r,t) constructed by local viscoelastic equivalence method

與0.125 g TNT 填實爆炸下花崗巖中粒子速度實測位置相對應，圖11～12 分別給出了花崗巖中不同位置的徑向應變 εr(r,t)和 切向應變 εθ(r,t)（以壓為負）。可以看出，半徑15～50 mm 范圍內，花崗巖中徑向應變峰值由?1.7×10?2下降為?2.1×10?3，切向應變峰值由4.7×10?3下降為0.4×10?3。另外，從圖11～12 還可看出，徑向和切向應變達到峰值后降低一段時間，而后又發生一定的上升，這和盧強等[24]給出的理論模擬結果體現的變化規律一致。

圖 11 花崗巖中的徑向應變Fig. 11 Radial strain in granite at different radii

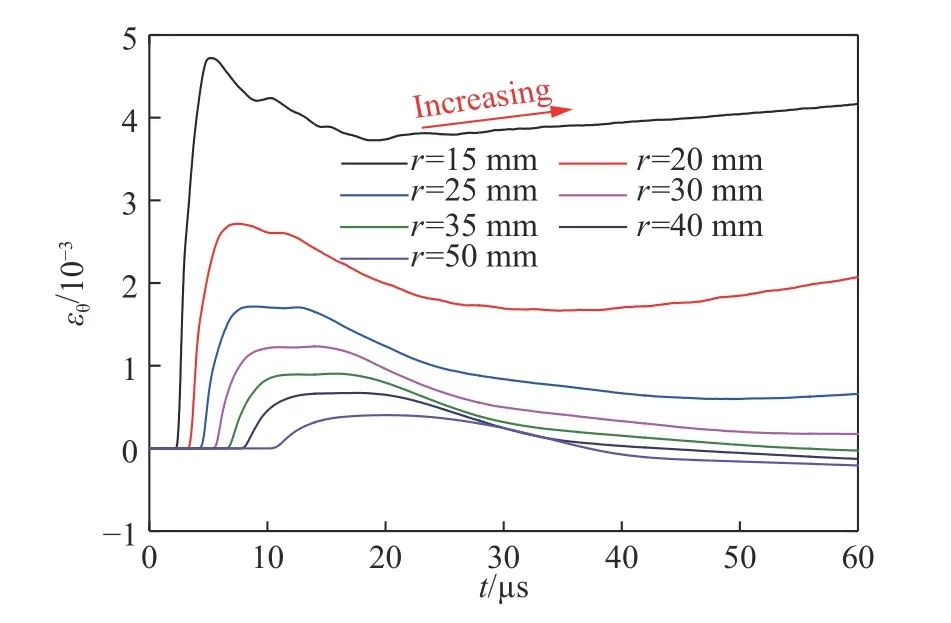
圖 12 花崗巖中的切向應變Fig. 12 Tangential strain in granite at different radii

圖13～14 分別給出了花崗巖中不同位置的徑向應變率 ε˙r(r,t) 和 切向應變率 ε˙θ(r,t)。由圖13 可以看出，徑向應變率 ε˙r(r,t)在μs 級時間內由壓縮加載轉變為拉伸卸載。隨著波傳播距離的增加，徑向壓縮加載應變率峰值由?5.1×104s?1下降為?2.5×103s?1，徑向拉伸卸載應變率峰值由3.5×104s?1下降為5.0×102s?1。由圖14 可以看出，隨著波傳播距離的增加，切向拉伸加載的應變率峰值由5.0×103s?1下降為1.4×102s?1，切向壓縮卸載的應變峰率值由?2.0×102s?1下降為?4.0×101s?1。從上述這些數據可以看出，在半徑15～50 mm 區域內應變（率）峰值約有一個數量級的變化，涵蓋了高應變（率）到中低應變（率）加、卸載的全過程。

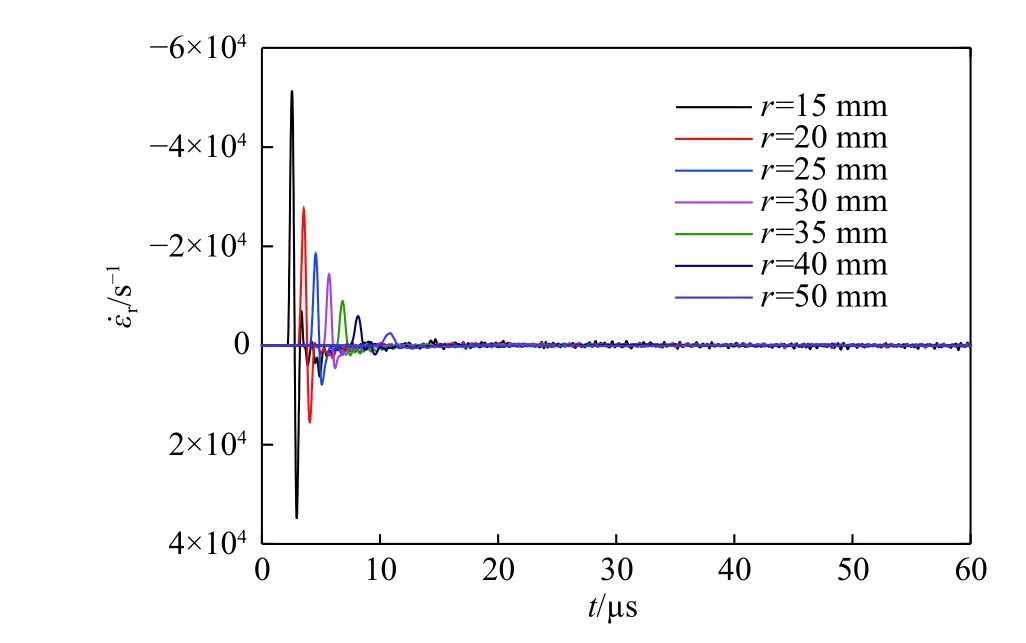
圖 13 花崗巖中的徑向應變率Fig. 13 Radial strain rates in granite at different radii

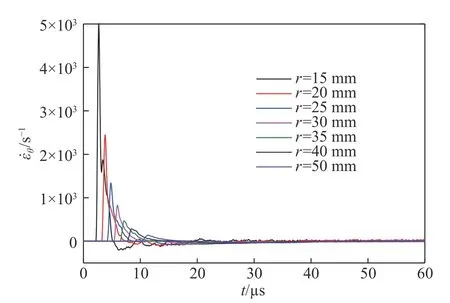
圖 14 花崗巖中的切向應變率Fig. 14 Tangential strain rates in granite at different radii

圖15 給出了花崗巖中不同位置的應變狀態。可以看出，爆炸近區應變狀態 εr- εθ主要為壓拉模式，隨著波傳播距離的增加，開始逐漸出現拉拉、拉壓、壓壓模式。由靜態分析結果可知，當填實爆炸激發的爆腔壓力穩定時，介質的應變狀態 εr- εθ為壓拉模式[24-25]。這里需指出，圖15 中給出的花崗巖不同位置的應變狀態 εr- εθ最終會穩定在壓拉模式。由于樣品邊界反射波的影響，圖15 中遠離爆心的幾個位置的應變狀態并不完整，其最終應變狀態 εr-εθ沒有處于壓拉模式。

圖 15 花崗巖中不同位置的應變狀態Fig. 15 Strain states in granite at different radii

5 結 論

由上述分析得到以下幾點結論：

（1）利用花崗巖中實測的粒子速度頻譜信息，計算得到的衰減因子 α(ω)和 波數 k (ω)反映出了爆炸應力波從近區的高壓狀態演化到相對遠區的低壓狀態時花崗巖對波吸收和彌散的頻率相關性；

（2）花崗巖中波傳播系數隨爆心距的增加而變化，即使是在確定的彈性區內傳播的低幅值弱波，花崗巖表現出來的也不是理想的黏彈性力學行為。換言之，花崗巖的波傳播系數對其所處的應力應變狀態敏感；

（3）以花崗巖中相鄰測點之間區域內局部黏彈性等效假設為基礎，分區域構建了填實爆炸下花崗巖介質運動和變形的時空分布，其處理精度高于局部彈性等效方法；

（4）0.125 g TNT 填實爆炸下，在半徑15～50 mm 區域內：花崗巖的應變狀態 εr-εθ主要為壓拉模式，隨著波傳播距離的增加，開始逐漸出現拉拉、拉壓、壓壓模式；花崗巖的徑向應變率很快由壓縮加載轉變為拉伸卸載，而切向應力率則由拉伸加載轉變為壓縮卸載；應變（率）峰值約有一個數量級的變化，涵蓋了高應變（率）到中低應變（率）加、卸載的全過程；

（5）球面波傳播過程中其頻率成分不斷發生變化，部分頻段的粒子速度信息由于粒子速度計無法響應（或響應精度降低）、測試記錄設備精度不足、樣品尺寸小導致信號低頻成分未能充分發展、空間電磁干擾等一系列原因將影響數據的分析精度；

（6）根據本文中提出的構建地下爆炸介質運動及變形場的新方法，可進一步豐富對地下爆炸復雜應力應變狀態下介質變形特征的認識。