半解析法求解水柱分離與斷流彌合水錘問題及機理分析

韓 凱，丁法龍，茅澤育

半解析法求解水柱分離與斷流彌合水錘問題及機理分析

韓 凱，丁法龍，茅澤育※

（清華大學水利水電工程系，北京 100084）

為了應對長距離輸水工程的水錘防護問題，分析了空氣閥作用于波狀管線有壓輸水系統發生水力過渡時的瞬態響應過程，提出了空穴增長和潰滅時間、管線最大含氣率、最大壓力峰值等參數的半解析公式，并由此探討和研究影響空氣閥水錘防護效果的關鍵因素。半解析解表明，位于空氣閥下游的管段相對長度和管線高點的相對高程對系統的斷流彌合水錘起了主導作用。將半解析解與特征線法數值解進行了對比，發現兩者隨主變量的變化趨勢一致；分析了半解析解與數值解產生偏差的原因與半解析公式推導過程中幾個假設的關系。結果證明，該文提出的半解析公式能夠反映空氣閥作為水錘防護裝置時，主導斷流彌合水錘壓力峰值的關鍵因素。該研究可為水錘防護的相關研究提供參考。

壓力；模型；空氣閥；半解析方法；液柱分離；斷流彌合；特征線方法

0 引 言

在水力過渡過程中，有壓輸水管線內部產生真空，需要通過空氣閥將外界氣體引入管道[1-4]。空氣閥工作時既要保證吸入足量空氣以緩解負壓，又必須在真空負壓消失后盡快將氣體安全地排出管道，從而避免管內氣團滯留帶來的不利影響[5-7]。相比于調壓井和空氣罐等水錘防護裝置，空氣閥設計與布置更靈活，經濟性較高，因此在停泵、充放水、流量調節等操作引起水錘負壓時常被采用[8-10]。空氣閥的布設位置和孔口尺寸對有效控制管線內的真空條件至關重要，不當設計和故障失靈都極有可能引起二次水錘現象，引發更為嚴重的后果，但如何規避這一風險仍然存在較大的爭議[1, 4, 11-12]。

為了限制有壓輸水管道內部氣團積聚，按照空氣閥的使用指導意見，裝置常被要求布置在管線沿程的所有局部高點[13-14]，但這樣的方案經常導致安裝過多的空氣閥。因空氣閥需要定期進行檢查和維護，過量安裝必然會增加由于空氣閥故障引起二次水錘的風險[7,15]。因此，無論是從空氣閥的運維成本還是從空氣閥故障導致的不利影響考慮，減少冗余的空氣閥布置都具有積極意義。

用數值方法求解水力過渡過程的動力學方程組及相關邊界條件是一種較為可靠的方法，因此國內外學者們針對液柱分離現象和空氣閥開展了大量的數值研究工作，但數值方法計算量巨大；泵站水錘的水動力學特性對邊界條件又極其敏感，決定不同工程的水錘特性可能存在較大差異，因此針對某項輸水工程往往需要擬定數十甚至上百種工況，并進行計算和分析[16-23]。解析公式通過直接求解微分方程得到，變量間關系簡捷明了，便于分析計算，但解析解往往需要一些簡化條件或僅適用于特定的情況[24]，推廣應用受一定的限制。不同于數值方法的“暴力解”，半解析方法不僅物理意義清晰、直觀，而且適用面更廣、更具一般性，也有利于工況擬定和關鍵參數開展進一步研究，可以大大提高工程計算效率[25-26]。

從水錘波傳播的基本理論出發，針對本文設計的波狀管線有壓輸水系統，建立了發生水力過渡時空氣閥引起氣穴增長、潰滅的時間和與之對應的管道最大含氣率和水錘壓力峰值的半解析公式，并由此探討和研究空氣閥對系統的瞬態響應特點與輸水管線幾何特性和水力特性的關系。

1 水錘波傳播過程分析

如圖1所示，該有壓輸水系統主要由上、下游水庫、泵、空氣閥和帶有局部高點的輸水管線構成，管道材料、截面形狀和面積沿程不變。將上游水庫A1到局部高點B的長度為1的管段（A1B）定義為上游段，將局部高點B至下游水庫C的長度為2的管段BC）定義為下游段。當輸水流量恒定時，忽略局部水頭損失，沿程水頭均勻變化。

注：A1為上游水庫，C為下游水庫；B為局部高點，布置有空氣閥；h1與h2為上游端和下游端的水頭，m；hp為B點的水頭與高程的差值，m；v0為水流流速，v0= q0/A，m·s-1；q0為初始管道流量，m3·s-1；A為管道的截面積，m2；L1與L2為上游段和下游段的管線長度，m。

在=0時刻，事故停泵引起斷流后，閥門隨即關閉，在上游端形成一個大小為Δ1的降壓波。當降壓波經過1/的時間傳播到B點時，空氣閥開啟，引入空氣使得B處壓強總維持在大氣壓。一方面，在B處的氣團作用下，降壓波的大小從Δ1減弱為h后繼續向下游傳播；另一方面，水錘波在氣團處產生反射，繼而向上游傳播大小為Δ2的增壓波，其中Δ2=Δ1?h。1/時刻后，A1B段的水流和水錘波將做周期性運動，忽略管道摩擦，B點在上游界面的水流速度up（由A1到B為正向）和水頭up可用圖2表示。

注：hB為局部高點處的水頭，m；Δh1為因停泵在上游端產生的降壓波，m；Δh2為在氣團處反射向上游端的增壓波，m；hup為局部高點在上游界面的水頭，m；vup為B點在上游界面的水流速度，m·s-1；t為時間；a為水錘波波速，m·s-1。

大小為h的降壓波繼續沿BC段向下游傳播，相應的流速從0減小為1

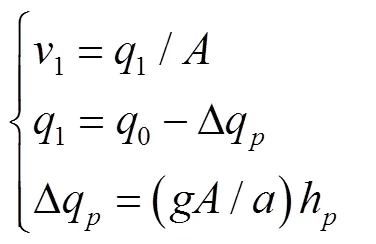
式中和′表示時間，s，′=1/；1為0<′<2/時下游管道內的流量，m3/s；為重力加速度，m/s2。

′=2/時刻降壓波抵達下游水庫后，向上游反射大小為h的增壓波，同時管道流量變為2（流向不變），即2/<′<22/期間，2=1?Δq，Δq為不計摩擦時下游流量變化值，q+1= q-Δq，m3/s；q為下游管段內的階段性流量，=1,2,…，m3/s；′=22/時刻水錘波再次抵達B點，水錘波在氣團處產生反射，繼而向下游傳播大小為Δ2的降壓波，由于不考慮管線摩擦且氣團體積相比于管線容積可忽略不計，使22/<′<32/期間3=2?Δq；此過程持續進行。當水錘波第次通過下游管段時，管道流量記為q；直到BC段水流正向流動停止，即q=0，此為第一階段。由于q>0時，BC段水體一直流入下游水庫，故外界氣體通過空氣閥持續進入管段，引起管內氣穴體積air增長。BC段正向流動停止時氣穴體積air出現最大值，但此時下游端水頭大于局部高點B處的氣壓，BC段水流開始逆向流動，air開始減小。逆向流速v+j每隔2/數值上增加Δv。Δv為下游段水流流速變化值，Δv= Δq/，m/s。此過程一直持續到管內氣體通過空氣閥被完全排出，A1B段水柱和BC段水柱重新彌合，即當air=0時下游段第二階段的流動停止。

B處形成的氣團隔斷了上、下游管段內的水體，因此可以將圖1所示的輸水系統拆解成2個子系統，以便進一步分析。根據前面分析所得的上、下游管段內水錘波不同的傳播特性，本文將圖1中的系統按圖3所示拆解成2個輸水子系統，其中：上游段的水錘由=0時刻的瞬時關閥引起，下游段子系統的水錘是由水庫在=1/時刻水位突然下降h引起。

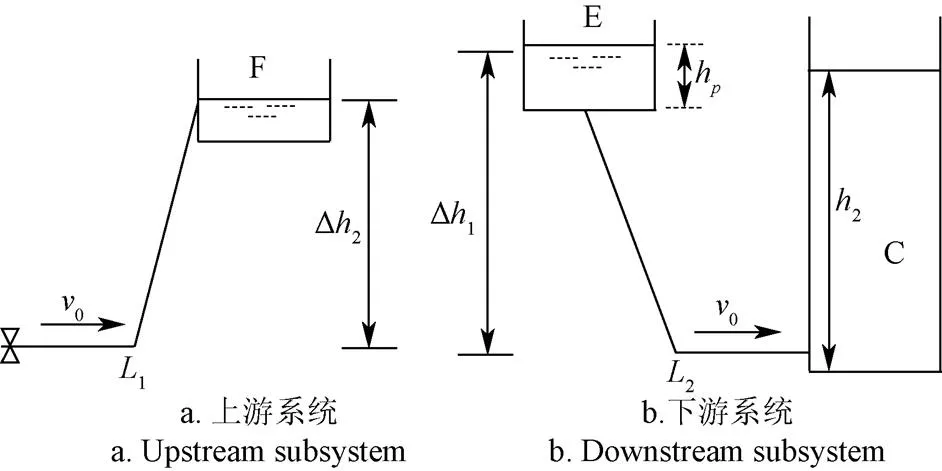
注：F、E為上、下游子系統中的2個水庫；hp為局部高點處的高程與該處水頭的差值，m。

2 半解析公式的建立

2.1 光滑管道的半解析公式

大小為Δ1的降壓波在B點削弱為P后，繼續向下游傳播，下游管段內的流量取決于B點的高程

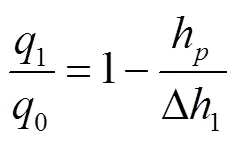
下游管段內流量q的變化還與下游管線的長度有關，利用取整函數INT（），下游管段內流量隨時間變化的函數q()可表示為

令式（3）等于0，得到下游段水錘波運動第一階段結束時傳播往返次數和相應的氣穴體積增長總歷時t。

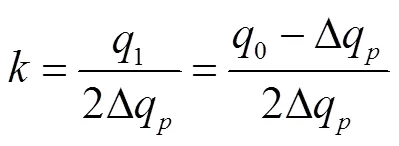
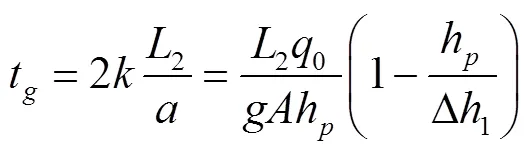
假設管內壓力變化時，氣體可以自由出入空氣閥，因為不計管道摩擦，可認為氣穴的增長過程和消減過程在時間上關于q=0的時刻對稱。由此，氣穴潰滅的歷時t可認為是氣穴體積增長歷時的2倍，即

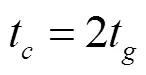
圖3所示等效的上游系統中，波的每次往返只引起水流流向周期性地反轉。因此，上游段水流流動對空穴體積的影響可以忽略不計。在下游段水流減速過程中，水體從管道進入下游水庫的同時，空氣不斷從空氣閥進入管道，于是下游管道的最大空穴體積airmax可表示為

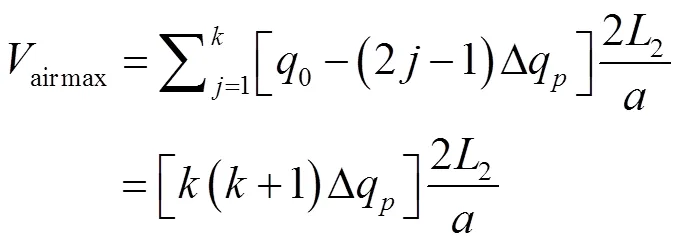
將式（2）至式（4）代入式（7），可得

由式（8）可知，最大空穴體積airmax是關于波在下游管道的傳播時間（2/）、橫截面積（）、初始管道流量（0）以及B點的相對高程（Δ2/Δ1）的函數。實際工程中、和0一般是確定的，因此airmax與2和Δ2/Δ1直接相關；airmax與2成正比，故當BC段管長較大時，更多氣體得以進入管道，但airmax與管道體積pipe（m3）的比值卻是恒定的。

假設氣體的體積流量與水流一致且不存在壓縮，在第二階段末空氣完全排出（air=0）時，空氣閥自動關閉，上下游水柱斷流彌合，產生水錘后同時向上下游傳播。該水錘壓力是Joukowsky公式計算值的一半[27]，即

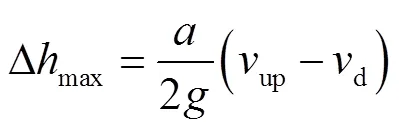
式中Δmax為光滑管道內上下游水柱斷流彌合產生的水錘壓力，m；up為上游管段的流速，m/s；d為下游管段的流速，m/s。結合式（4）并根據圖2考慮上游段對Δmax作用，可知不計摩擦時的最大和最小壓力峰值Δmax,min出現在管線A1B段水流停止運動（up=0）而內壓為±Δ2時，即

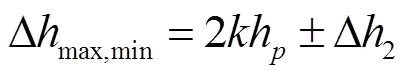
2.2 考慮摩擦影響的半解析公式

實際情況中水錘波在傳播過程中必然會因管線的摩擦作用而衰減，上游段的流量逐漸減少，上游段水錘波運動對管內氣穴體積air（m3）和Δmax的作用也會相應減少。考慮摩擦時，對t=2（1/）（=0,1,2,3…），上游段的流量變化q可用下面的階躍函數表示

式中in表示水錘波在B點第一次反射引起的流量，m3/s；h(q)表示流量q引起的沿程水頭損失，m。

顯然上游段不計摩擦時的流量變化過程只是式（11）的一個特例。對于下游段而言，管道摩擦使得流量變化減慢，從液柱分離到斷流彌合的歷時增加，airmax也隨之增加。結合變量Δ來描述流量和氣穴體積的變化，如下

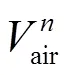
由式（12）可知，考慮摩擦作用時下游段流量q在水錘波傳播過程中的變化速率不斷變化，此處為了便于分析摩擦力的作用，假定式（13）中流量變化速率恒定，并由此得到關于上游段流量的衰減系數，如下

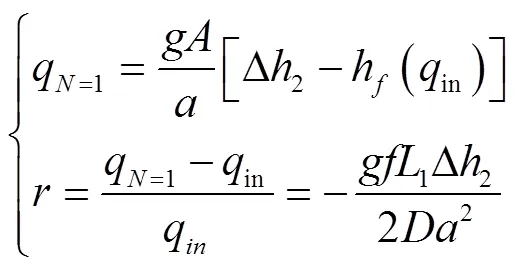
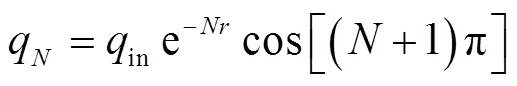
式中表示水錘波從=1/開始在上游段傳播的往返次數，q為水錘波第次往返傳播時的流量，m3/s。

為了估算上游段的水頭變化情況，將式（14）寫成B點水頭的形式，如下

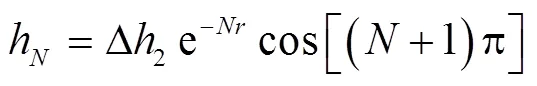
式中h為水錘波第次往返傳播時的上游管段水頭，m。

如前所述，下游段考慮摩擦時的流量增量變化更加復雜，為了便于討論，做以下假設：（1）無論是第一階段的正向流動，還是第二階段的逆向流動，流量增量均取平均值Δmean；（2）空穴消失和斷流彌合的時刻以逆向流量達到?1計。根據第（1）條假設，估算第一階段的流量增量平均值Δ1如下

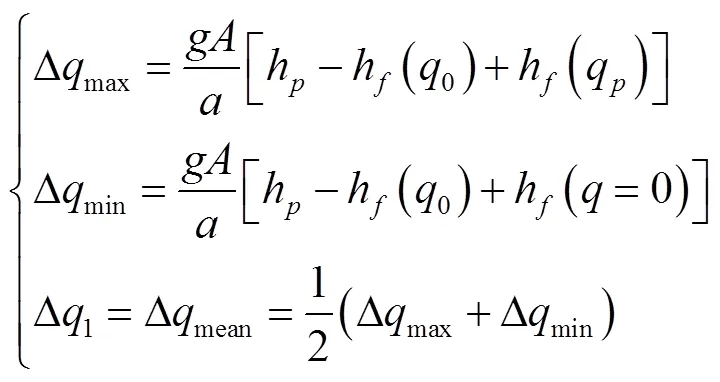
將式（16）中的Δ1代入式（3），得

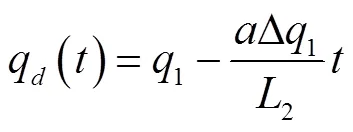
氣穴體積增長總歷時t出現在q()=0時，結合式（16）、式（17）及式（2），可得t的無量綱形式

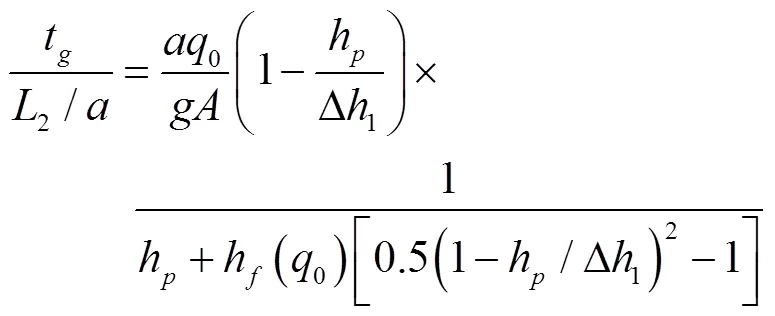
同理，可用式（19）估算下游段第二階段的流量增量平均值Δ2

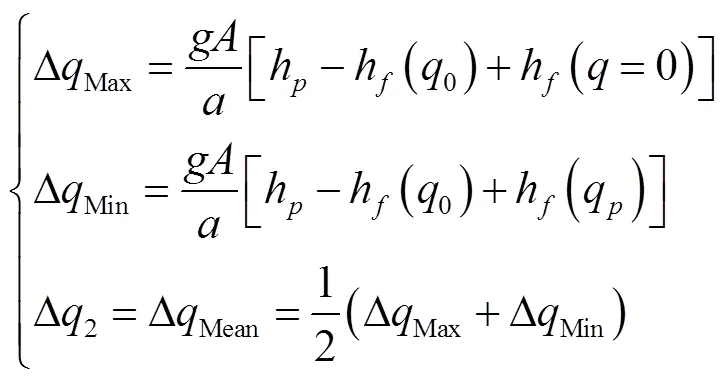
從t時刻至氣穴潰滅的總歷時t時刻，q()=0從0增長為-1，故有

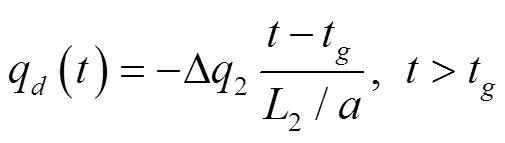
斷流彌合的時刻t出現在q()=?1，根據式（19）、式（20）及式（2），可得t的無量綱形式

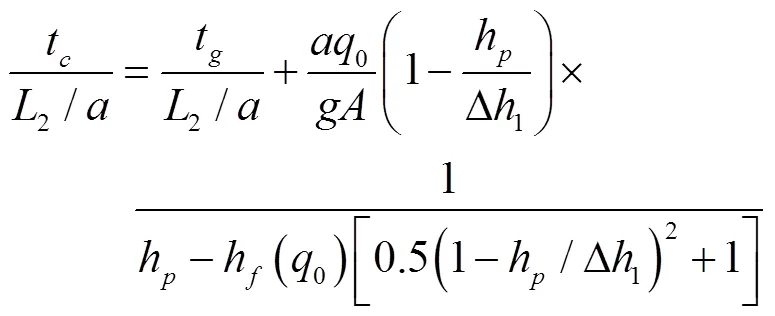
為了估計斷流彌合時的上游水頭和流量，有必要對該時刻水錘波往返傳播的次數N進行估計，即

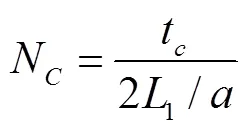
將N代入式（15）得到斷流彌合時的水錘壓力

最大空穴體積出現在=t時刻，相應的airmax可用式（17）在對應時段的積分來表示

將式（2）和式（18）代入式（14），得到下游管道最大含氣率max

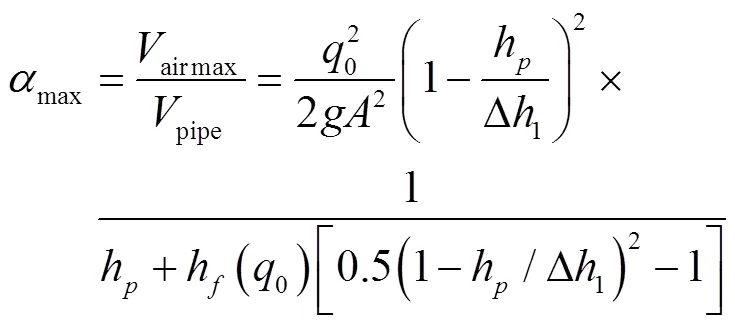
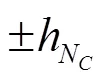
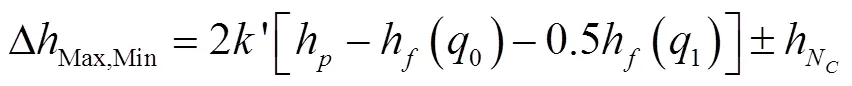
式中ΔMax,Min表示考慮管線摩擦時，上下游斷流彌合產生的最大和最小壓力峰值，m；表示考慮摩擦影響時下游段水錘波運動第一階段結束時的傳播往返次數。

圖4是令下游管線相對長度固定（2/1=10）后，取管線高點不同的相對高程（Δ2/Δ1）后，計算得到的t、t、max和ΔMax,Min。由圖4a可知，Δ2/Δ1越大，管線摩擦作用（取沿程阻力系數=0.022）對氣穴變化的作用更明顯，而且相比于t，t受管線摩擦作用的影響更顯著，這是因為摩擦作用使得下游段第二階段的流量增量Δ2大為減小。由圖4b可知，局部高點的高程越高，摩擦作用對水錘壓力的作用越明顯，管線的體積含氣量也就越大；不同Δ2/Δ1引起斷流彌合壓力峰值大小不同，當2/1=10時，最大壓力峰值ΔMax=1.54Δ1發生在Δ2/Δ1=0.85處。

注：tg為氣穴體積增長總歷時，s；tc為氣穴體積潰滅總歷時，s；f為沿程阻力系數；ΔhMax為考慮摩擦時的最大壓力峰值，m；ΔhMin為考慮摩擦時的最小壓力峰值，m。

對于下游管段不同的相對長度，斷流彌合產生的壓力峰值出現在不同的高程位置，這一趨勢可在圖5中體現：隨著下游管段相對長度2/1增大，出現壓力峰值ΔΔMax的相對高程不斷降低，ΔMax的值也逐漸減小；顯然這2種降低的趨勢隨著2/1增大不斷減緩，可見下游管段長度增加，壓力峰值ΔMax的大小和對應的高程位置會趨于穩定。

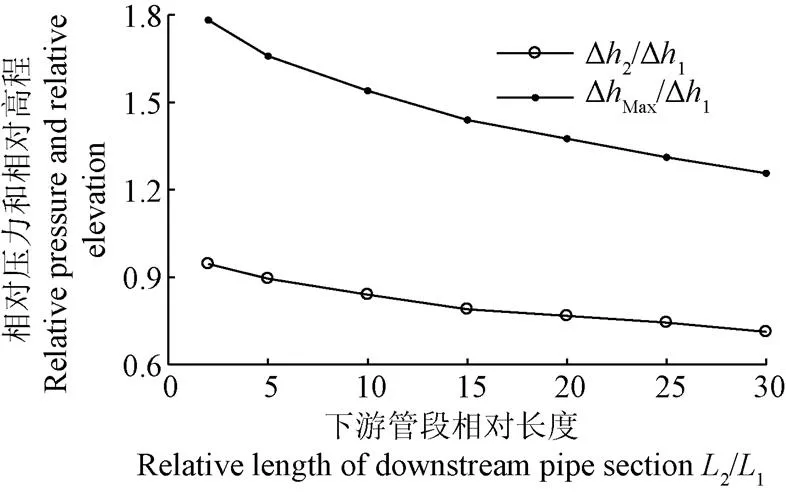
注：ΔhMax/Δh1表示斷流彌合水錘最大壓力峰值的相對值；Δh2/Δh1表示出現斷流彌合水錘最大壓力峰值對應的局部高點相對高程。

3 半解析法的驗證與誤差分析

一維非恒定有壓管流的連續性方程和運動方程如下[27]

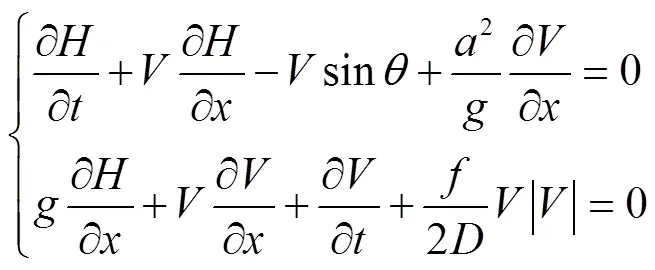
式中為斷面平均流速，m/s；為測壓管水頭，m；為管軸線上流動方向與水平線的夾角，rad，當高度沿軸正方向增加時為正；為沿程阻力系數。

特征線法（method of characteristics，MOC）是一種通過求解一維非恒定有壓管流連續性方程和運動方程及相關內外邊界條件來分析水力過渡過程中各類主要現象的數值計算方法，被學者們廣泛應用[17, 28-30]。本文為圖1所示的輸水系統設計不同的管線高點高程，建立數值模型后采用特征線法進行求解，并將數值計算結果與本文半解析方法（semi-analytic method，SAM）得到的結果進行對比，得到圖6。數值模型的主要參數如下：管徑= 2 m，初始流量0=1.0 m3/s，波速=1 000 m/s，上游管線長度1=1 km，下游管線長度2=101，沿程阻力系數為0.022，空氣閥進出孔口的直徑與流量系數分別為0.2 m、0.2 m、0.6和0.6。

如圖6所示，2種計算方法計算得到的氣穴增長時間t、氣穴潰滅時間t、管道最大含氣率max和斷流彌合壓力峰值ΔMax隨B點相對高程（Δ2/Δ1）變化的趨勢一致，且在數值上差異較小。其中，以半解析方法計算得到的max在數值上小于MOC方法計算得到的結果，這主要是因為在分析過程中忽略了上游段的儲氣量。2種方法計算得到的ΔMax存在一定差異，這可能是因為采用形如式（17）、式（20）和式（24）的線性函數來計算下游管段的流量會導致下游流量及相應斷流彌合水錘偏小，而用MOC計算水錘壓力時，空氣閥的邊界條件可控制計算過程中下游流量經過反射后按階躍形式變化，而Δ2/Δ1越小，根據2種方法計算得到ΔMax的數值隨著差異越大，這是因為管線高點越低，下游管段的坡度項sin越大，對MOC方法求解水錘壓力的影響也就越大。此外，半解析法假定第二階段逆向流量達到?1時刻發生斷流彌合，但實際當逆向流量達到?1時，管內氣體未完全排盡，因此MOC計算得到發生斷流彌合時候的流量會在?1的基礎上在附加部分流量，這無疑會使得MOC計算得到的t和ΔMax稍大于半解析法計算得到的數值，圖6表明管線高點越低這一現象越明顯，如Δ2/Δ1=0.9時，2種計算方法得到的t、t、max、ΔMax相對誤差是16.1%、12.8%、22.2%、4.9%，而當Δ2/Δ1=0.6時，相對誤差依次為是45.3%、47.4%、55.8%、14.6%。另一個引起兩者偏差的原因可能是采用式（16）和式（19）對兩階段的流量增量取了平均值。

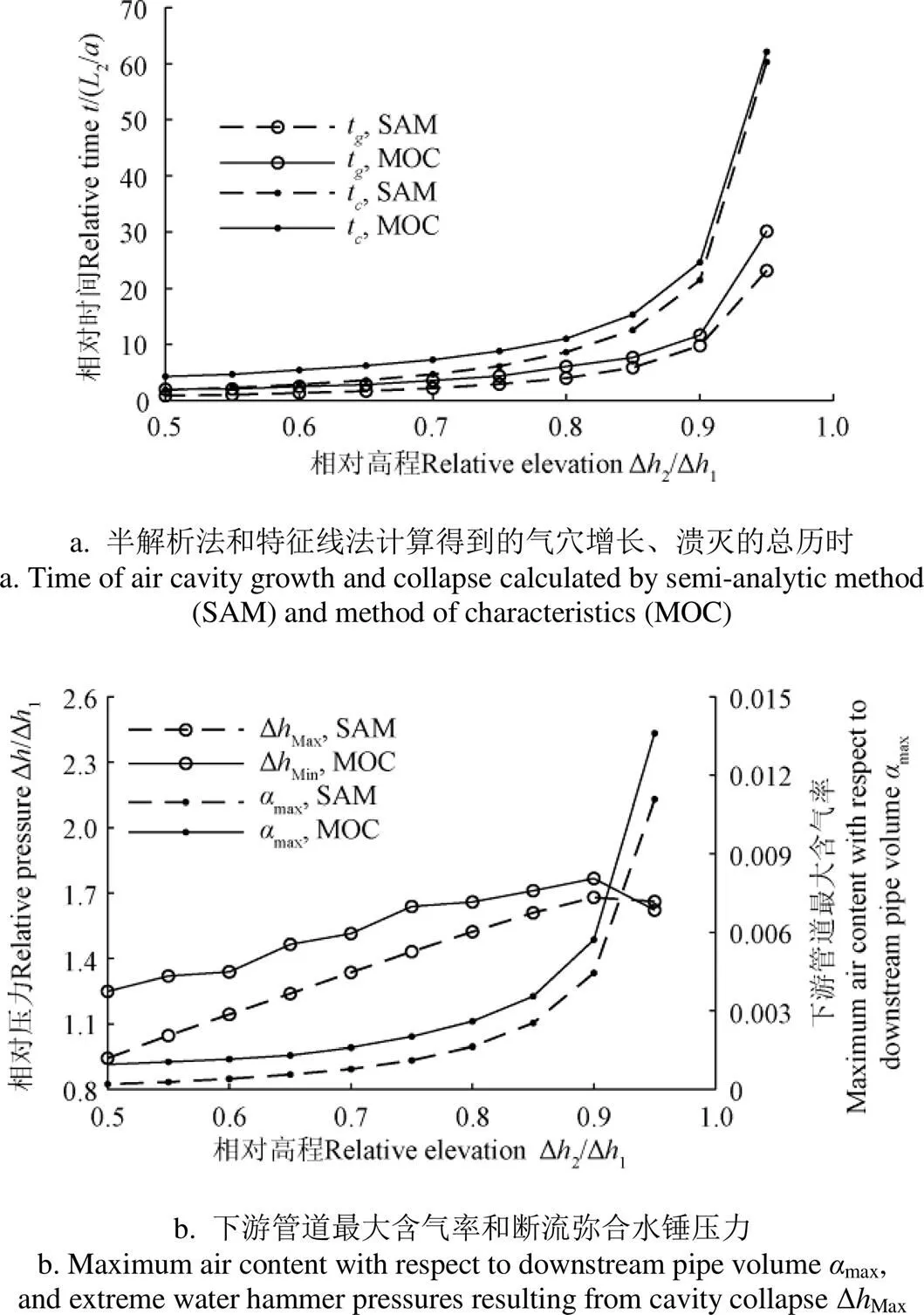
圖6 半解析法(SAM)與特征線法(MOC)求解結果的對比

雖然在半解析公式推導過程中幾點假設引起了系統誤差，但半解析解與數值解呈現了較好的吻合度，證明該半解析方法有助于正確理解空氣閥對系統的瞬態響應特點與輸水管線幾何特性和水力特性的關系。

4 結論與討論

針對設計的波狀管線有壓輸水系統，先后從無摩擦和有摩擦2種情況，就氣穴增長與潰滅時間、管道最大含氣量、氣穴潰滅時的最大和最小壓力峰值等目標參數推導了半解析公式，并據此對空氣閥的水錘防護機理進行了分析。主要結論如下：

1）目標參數的半解析公式表明，空氣閥下游管段的相對長度和管線高點的相對高程對系統發生水力過渡時的瞬態響應起了主導作用。

2）數值方法與半解析方法的計算結果存在一定的偏離，這可能是在公式推導過程中的幾點假設引起的系統誤差，可考慮通過后續的試驗引入參數加以修正；但2種方法的結果隨局部高點相對高程的變化趨勢一致，證明根據半解析公式得出的初步結論是正確的：管道最大含氣率與水錘波在下游管道的傳播時間和管線高點的相對高程正相關。因此隨著空氣閥安裝高程的增加，尤其是與之對應的下游管段長度較大時，空氣閥采用大口徑進氣孔有利于提高其水錘防護效果。

3）隨管線高點高程的增加，氣穴潰滅時的逆向流量和流速增大，導致對應的最大壓力峰值增大，但考慮管線摩擦作用時，最大壓力峰值出現在一個特定高程；峰值壓力及對應高程位置隨下游管段相對長度的增加而逐漸下降，最終趨于穩定。即空氣閥下游管段的長度和粗糙程度決定了最大壓力峰值及其出現的特定管線高程。

本文提出的半解析公式適用于包含一個空氣閥的波狀管線輸水系統，對于包含存在相互影響的多種水錘防護裝置的復雜系統，需要在今后的研究中討論。本文提出的半解析公式有助于理解空氣閥在水錘防護時的作用機理，明確應該基于那些條件對空氣閥的尺寸與布設位置進行調整，為有壓輸水系統，特別是那些沿途管線高程起伏波動的工程，選擇合適的空氣閥以及削減冗余的空氣閥提供了參考，使有壓輸水系統免受二次水錘和真空負壓的影響。

[1] Ramezani L, Karney B, Malekpour A. The challenge of air valves: A selective critical literature review[J]. Journal of Water Resources Planning and Management, 2015, 141(10):04015017.

[2] Coronado-Hernandez O E, Fuertes-Miquel V S, Besharat M, et al. Experimental and numerical analysis of a water emptying pipeline using different air valves[J]. Water, 2017, 9(2):98.

[3] Fuertes-Miquel V S, Lopez-Jimenez P A, Martinez-Solano F J, et al. Numerical modelling of pipelines with air pockets and air valves[J]. Canadian Journal of Civil Engineering, 2016, 43(12): 1052－1061.

[4] 劉志勇，劉梅清. 空氣閥水錘防護特性的主要影響參數分析及優化[J]. 農業機械學報，2009，40(6)：85－89.

Liu Zhiyong, Liu Meiqing. Analysis and optimization of main influencing parameters for water-hammer prevention characteristic of air valves[J]. Transactions of The Chinese Society of Agricultural Machinery, 2009, 40(6): 85－89. (in Chinese with English abstract)

[5] 王玲，王福軍，黃靖，等. 安裝有空氣閥的輸水管路系統空管充水過程瞬態分析[J]. 水利學報，2017，48(10)：1240－1249.

Wang Ling, Wang Fujun, Huang Jing, et al. Filling transient analysis in pipelines with air valves[J]. Journal of Hydraulic Engineering, 2017, 48(10): 1240－1249. (in Chinese with English abstract)

[6] Carlos M, Arregui F J, Cabrera E, et al. Understanding air release through air valves[J]. Journal of Hydraulic Engineering-ASCE, 2011, 137(4): 461－469.

[7] Bergant A, Simpson A R, Tijsseling A S. Water hammer with column separation: A historical review[J]. Journal of Fluids and Structures, 2006, 22(2): 135－171.

[8] 高金良，鄭成志，刁美玲，等. 高起伏長輸管線水錘模擬及防護方案優選[J]. 哈爾濱工業大學學報，2012，44(8)：24－26，38.

Gao Jinliang, Zheng Chengzhi, Diao Meiling, et al. Study on optimal surge protection for high-undulate long-distance water transmission pipeline[J]. Journal of Harbin Institute of Technology, 2012, 44(8): 24－26, 38. (in Chinese with English abstract)

[9] 胡建永，張健，索麗生. 長距離輸水工程中空氣閥的進排氣特性研究[J]. 水利學報，2007(增刊1)：340－345.

Hu Jianyong, Zhang Jian, Suo Lisheng. Study on air admission and exhaust characteristics of air valve in long water supply system[J]. Journal of Hydraulic Engineering, 2007(Supp.1): 340－345. (in Chinese with English abstract)

[10] Ramezani L, Karney B. Water column separation and cavity collapse for pipelines protected with air vacuum valves: Understanding the essential wave processes[J]. Journal of Hydraulic Engineering, 2017, 143(2): 04016083.

[11] Lingireddy S, Wood D J, Zloczower N. Pressure surges in pipeline systems resulting from air releases[J]. Journal American Water Works Association, 2004, 96(7): 88－94.

[12] Coronado-Hernandez O E, Fuertes-Miquel V S, Angulo- Hernandez F N. Emptying operation of water supply networks[J]. Water, 2018, 10(1):22.

[13] Howard G. Water Supply Surveillance: A Reference Manual[M]. WEDC, Loughborough University, 2002.

[14] John D M. Awwa manual of water supply practices: M57. 1ST ED[J]. Journal of Phycology, 2011, 47(4): 963－965.

[15] De Aquino G A, De Lucca Y D L, Dalfre J G. The importance of experimental tests on air valves for proper choice in a water supply project[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40(8):403.

[16] Jiang D, Ren C, Zhao T Y, et al. Pressure transient model of water-hydraulic pipelines with cavitation[J]. Applied Sciences-Basel, 2018, 8(3):388.

[17] Riasi A, Tazraei P. Numerical analysis of the hydraulic transient response in the presence of surge tanks and relief valves[J]. Renewable Energy, 2017, 107: 138－146.

[18] 富友，蔣勁，李燕輝，等. 改進雙流體模型計算有液柱分離的管路水錘壓力[J]. 農業工程學報，2018，34(15)：58－65.

Fu You, Jiang Jin, Li Yanhui, et al. Calculation of pipe water hammer pressure with liquid column separation by improved two-fluid model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(15): 58－65. (in Chinese with English abstract)

[19] Zhang B R, Wan W Y, Shi M S. Experimental and numerical simulation of water hammer in gravitational pipe flow with continuous air entrainment[J]. Water, 2018, 10(7):928.

[20] Zhou L, Wang H, Bergant A, et al. Godunov-type solutions with discrete gas cavity model for transient cavitating pipe flow[J]. Journal of Hydraulic Engineering, 2018, 144(5): 04018017.

[21] Geng J, Yuan XL, Li D, et al. Simulation of cavitation induced by water hammer[J]. Journal of Hydrodynamics, 2017, 29(6): 972－978.

[22] Moghaddas S M J. The steady-transient optimization of water transmission pipelines with consideration of water-hammer control devices: A case study[J]. Journal of Water Supply Research and Technology-Aqua, 2018, 67(6): 556－565.

[23] 王振華，馬習賀，李文昊，等. 基于改進4-方程摩擦模型的輸水管道水錘壓力計算[J]. 農業工程學報，2018，34(7)：114－120.

Wang Zhenhua, Ma Xihe, Li Wenhao, et al. Calculation of water hammer pressure of flow pipeline based on modified four-equation friction model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 114－120. (in Chinese with English abstract)

[24] Fan C Y, Zhang J, Yu X D. Analytical solutions for predicting the maximum pressure drop after pump failure in long-distance water supply project[J]. Water Science and Technology-Water Supply, 2018, 18(6): 1926－1936.

[25] Pandey R K, Mishra H K. Semi-analytic numerical method for solution of time-space fractional heat and wave type equations with variable coefficients[J]. Open Physics, 2017, 15(1): 74－86.

[26] Dai Y, Yan X, Sun C, et al. Semi-analytic numerical method for structure analysis of functionally graded materials[J]. Proceedings of the International Conference on Mechanical Engineering and Mechanics, 2007, 1(2): 1317－1321.

[27] Wylie E B, Streeter V L, Suo L. Fluid Transients in Systems[M]. Englewood Cliffs: Prentice Hall, 1993.

[28] Ghidaoui M S, Ming Z, McInnis D A, et al. A review of water hammer theory and practice[J]. Applied Mechanics Review, 2005, 58(1): 49－76.

[29] Wan W Y, Li F Q. Sensitivity analysis of operational time differences for a pump-valve system on a water hammer response[J]. Journal of Pressure Vessel Technology- Transactions of the Asme, 2016, 138(1):011303.

[30] Meng W W, Cheng Y G, Wu J Y, et al. GPU acceleration of hydraulic transient simulations of large-scale water supply systems[J]. Applied Sciences-Basel, 2019, 9(1):91.

Solving water column separation and cavity collapse for pipelines by semi-analytical method

Han Kai, Ding Falong, Mao Zeyu※

(,,100084,)

For pressurized water supply systems, excessive installation of air valves will inevitably increase the risk of secondary water hammer especially when the air valve fails. Therefore, reducing redundant air valves is of positive significance whether from the maintenance cost on apparatus or from the possible adverse impact caused by the malfunction. Compared to traditional analytical and numerical methods, the semi-analytical method adopted in this paper could not only ensure the clear and intuitive physical meaning of the research results but also expand the application scope of the analytical method, which was also conducive to the further study of key parameters. In this research, it aimed to find out the primary relationship between the function of air valves and the geometry characteristic of the system. Taking a simplified reservoir-pipe-reservoir system with one air valve installed at the elevated point for example, the research initially employed the basic theory of fluid transients to analyze the water hammer wave propagation process. Since the gas inhaled through the air valve separated the water column as the depressurized pressure arrived at the elevated point, the system was divided into 2 subsystems at the point according to their different wave propagation processes. The semi-analytical formulas of the target parameters such as the duration time of cavity growth and collapse, maximum air pocket volume and extreme pressure spike， were firstly proposed in a frictionless condition. Based on the formulas, it studied the key factors affecting the protective effect of the air valve against the water hammer. The semi-analytical solution indicated that the relative length of the downstream pipe section and the relative elevation of the high point played a leading role in the process of cavity growth and collapse. The effect of friction was later taken into the consideration of the semi-analytical expressions serving to reveal its influences on the system. Numerical simulations established on the method of characteristics, which had been proved to a credible and effective numerical method, were then conducted and compared with the semi-analytical solutions to validate the corresponding expressions with and without friction. The outcomes of the 2 approaches presented a consistent variation tendency with the principle variable. However, deviations still existed particularly when the targeted point had a relatively low elevation. The reasons for above deviations were discussed which probably stemmed from some hypotheses during the derivation of semi-analytic formulas, mainly including the omission of gas storage in the upstream section, linear and averaging treatment of the flow variation process in the derivation step. It could also be speculated from the results that the length and roughness of the downstream pipeline determined the maximum pressure spike and the specific pipeline elevation. The semi-analytical formula proposed in this paper was applicable to the containing-one-air-valve pressurized water supply system, and it required to be discussed in the future research for the complex system containing multiple water hammer protection devices with mutual influence. In spite of the limitations, the semi-analytical formulas still reflected the key factors correctly of the air valve as the protection device against water hammer. The findings are helpful to understand the action mechanism of the air valve in the hydraulic transition and provide references for the research of water hammer protection.

pressure; models; air valve; semi-analytical method; water column separation; cavity collapse; method of characteristics

10.11975/j.issn.1002-6819.2019.15.005

TV131.2

A

1002-6819(2019)-15-0033-07

2019-03-24

2019-07-19

國家重點研發計劃（2016YFC0402504）

韓 凱，博士生，主要從事水力學與河流動力學方面研究。Email：hk17@mails.tsinghua.edu.cn

茅澤育，教授，博士生導師，主要從事水力學與河流動力學方面研究。Email：maozeyu @tsinghua.edu.cn

韓 凱，丁法龍，茅澤育. 半解析法求解水柱分離與斷流彌合水錘問題及機理分析[J]. 農業工程學報，2019，35(15)：33－39. doi：10.11975/j.issn.1002-6819.2019.15.005 http://www.tcsae.org

Han Kai, Ding Falong, Mao Zeyu. Solving water column separation and cavity collapse for pipelines by semi-analytical method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(15): 33－39. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.15.005 http://www.tcsae.org