基于建構主義思想 解讀中學生認知困惑
——以追問及思考的幾個幾何光學問題為例
劉璐璐 張皓晶
(云南師范大學物理與電子信息學院,云南 昆明 650500)
建構主義教學思想不僅對我國教學理論與教學實踐改革產生了巨大影響,對全世界的其他國家的教育實踐改革也都產生了巨大的影響.它促使我們變革舊有的教育觀念,確立了以學生為主體的教學觀.建構主義思想認為,教師應當把學生視作一個自我構建自己知識體系的自生產系統.通過對高中生思維特點的分析,筆者發現:高中生尚處于“由形象思維和感性思維”向“抽象思維和理性思維”發展的過渡時期,很多時候仍然沿襲初中時的定性思維方式,容易產生錯誤的思維傾向.并且很大一部分的高中生都缺乏發散性思維,思維水平上存在著片面性、表面性.因此,作為新生一代的物理教師,學習建構主義教學方法,做好學生學習的“引路人”將是十分必要的. 一直以來,高中物理教師幾乎都是按照教科書上的章節內容安排來進行授課的.這種教學方式自然有其優勢,但同時也存在缺陷.缺陷就在于,如果教師直接引入高中的知識內容,而不在初中已有的知識基礎上建構,學生會出現知識斷層的狀況,成了“知識的容器”.因此,在引入與初中知識有關聯的高中內容時,需要教師主動將學生過去的經驗與當下所學的內容有效結合起來.
教師首先需要明確這樣一點:既然學習者不是被動接收知識的,而是主動建構知識的.那么,對學習者先前知識的注意就應當成為教學工作的一個十分重要的基本要素.教師要做的就是幫助學生去發現、去質疑、去主動建構,這也是在物理教學中培養學生核心素養的關鍵點.同時,這種建構主義的觀念在教學方面也給教師一種啟示,即教師需要依據教學大綱和學生的知識經驗特點,避免對單一知識的過度關注,從整體角度把握教學需求,整合教學內容與相關資源,引導學生做好知識建構,提升高中生的物理學科素養.下面以教學過程中引起學生困惑的兩個光學問題為例,就建構主義思想引入高中光學課堂做一個闡述,以期為中學物理教師的教學提供參考.
1 為什么瞄準魚頭叉不到魚,而用激光照射卻能射中?[1]
1.1 建構起點——學情分析
雖然高中物理教材人教版選修3-4的光學章節中,對光的折射定律已有較為深入的講述及應用,但光線的引入畢竟是一種建模,對學生而言分析難度較大,對他們的抽象思維能力來說更是一種挑戰.如果學生在學習過程中不注意把握折射的知識點,學會幾何光學問題的分析方法,將初中定性分析問題的方法轉化成高中定量的幾何光學問題的分析方法,便容易產生疑惑.在學生學完初中光的折射內容后,他們就已經知道了池水看起來比實際的淺,是由于池底某點發出的光從水中斜射向空氣時會發生偏折,所以逆著折射光看去就會感覺這點的位置升高了.利用同樣的道理,學生們也一定會知道瞄準魚的下方可以叉到魚,而對準魚叉魚是叉不到的.[2]
1.2 建構策略——引入問題,引發認知沖突
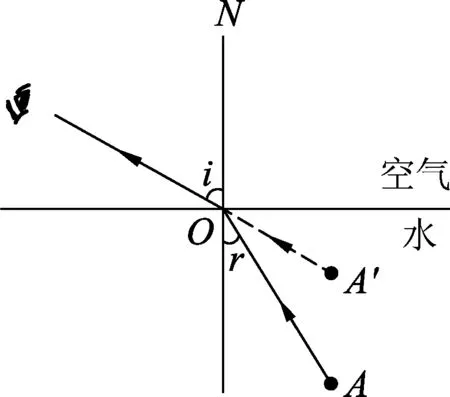
圖1 水下反射回人眼的光路與激光照射水下物體的光路
那么魚為什么能被激光光束射中呢?在這里,學生已經學習了高中光的折射定律,教師便可對學生進一步提問,讓他們在已有學習經驗的基礎上做出自己的分析.這便自然地引發了學生的認知沖突,激發了學生想要進一步探求真理的欲望.當然,在這里教師除了要使學生內部認知系統獲得調節順應外,還應當要教會學生作圖輔助的思維方法.
1.3 建構過程——分析問題,解除困惑,學生完成提升
如圖1所示,O為法線與分界面的交點,N為法線,i為入射角,r為折射角.學生們根據已有的經驗就已經知道了人眼看到的水下的魚,實際上是位于A點折射到人眼的光線形成的.因此,人用鋼叉沿入射光線經O點往下叉,顯然是叉不到魚的.那為什么用激光就能射中魚呢?原因在于激光沿入射光線方向射向界面交點O點,會在不同介質分界面上發生偏折,而偏折的光線就會偏折到我們人眼看到的魚像對應的真實實物上,也即真實的魚上,所以激光可以射中魚.
1.4 教學啟示
在教學過程中,教師應當注意運用建構主義的思想,幫助學生在其初中的光折射知識基礎上不斷深化,達到能靈活運用所學知識,解釋生活中與光折射有關的一些問題的程度.教師在日常教學中,也應當合理巧妙地創設認知沖突,使學生在解決認知沖突的同時,掌握學習方法、理解知識內涵、提升科學素養.在原有認知沖突解決后,還需不斷使學生產生新的認知沖突,以使他們對該問題的認識不斷深入,思維水平不斷提升.最終使他們的思維空間更加開闊,實現“舉一反三”.
與迂腐的教學形式、被動灌輸式的教學相較,此處知識的獲得是通過學生與教師的共同思索得來的,更強調學習者在認知過程中的中心地位,即學生主體的事實.教師要做的就是探索幫助學生構建知識體系的過程、方法——引導學生發生認知沖突,使他們產生不斷學習的欲望.
2 物在何方?
從空氣中觀察處于水下的物體,物體的實際位置在人眼看到的像的哪一邊?左下方還是右下方?從水下觀察空氣中的物體呢,情況又是怎樣的?
2.1 建構起點——學情分析
在解決此類問題時,學生已經具備了初中的相關知識內容基礎,也初步學習了高中光的折射與反射定律的內容,并具備了相當的數學幾何知識.但就物理學科素養的培養目標而言,現階段的學生在分析、綜合、解決實際問題方面仍存在很大困難,對知識的理解圄于表面,對物理過程的分析停留在淺層次.
2.2 建構策略——借助案例,學會查閱文獻,自主分析解決問題
設置這一問題,能夠讓學生產生濃厚的興趣,讓他們更想自主地去探究光學中的物理規律.一則這類問題是原先的物理舊情景,學生熟悉;二則在舊情景上產生了新內容,學生不會覺得乏味.教師也可以借助這個例子,讓學生更深入地理解幾何光學的知識內容,使他們在原有基礎上拔高,可謂“一石二鳥”.這里教師可做適當引導,教學生查閱資料、翻閱文獻,并可在下次課上做出解答,教會他們如何分析此類問題.
2.3 建構過程——分析問題,解除困惑,學生完成提升
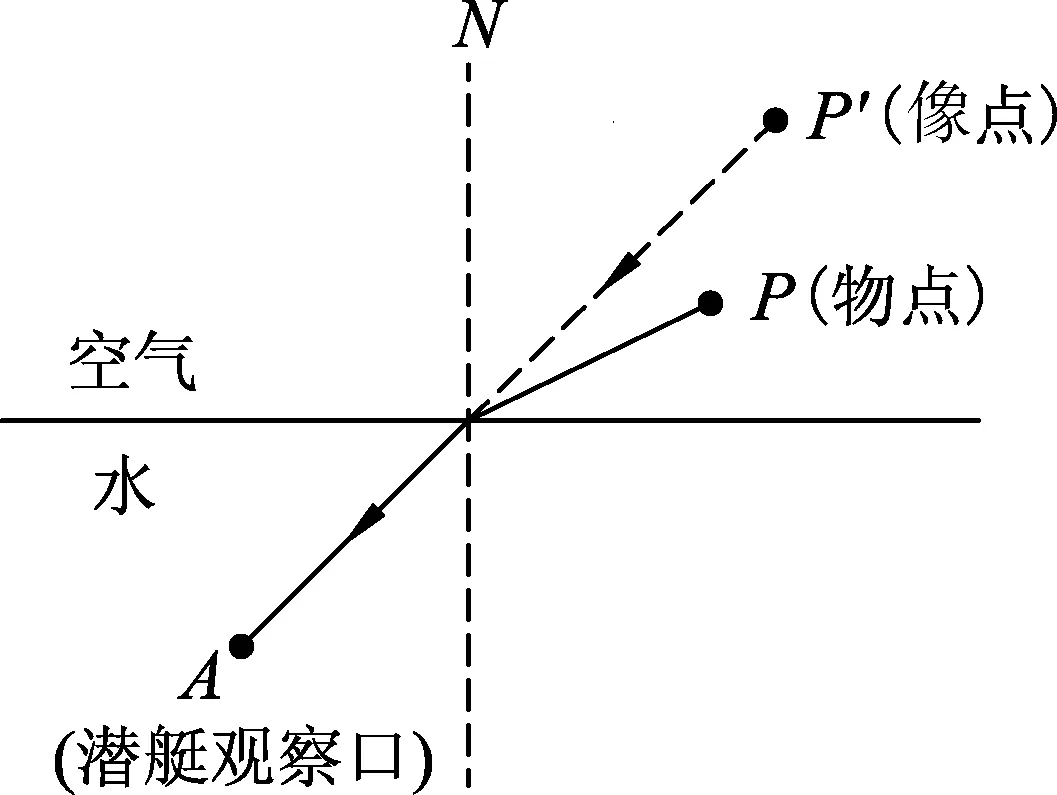
假設空氣的折射率為n2,水的折射率為n1,n2 圖2 從空氣中觀察水下物體的光路 如圖2中,以x軸代表兩種介質的分界面,以OP為y軸,則P點的坐標為(0,y),假設如圖有兩條光線PM1、PM2,入射點M1的坐標為(x1,0),M2的坐標為(x2,0),PM1入射角為i1,PM2入射角為i1+di1,折射角則分別為i2,i2+di2.兩條射線M1N1,M2N2向后延長分別交y軸于P1(0,y1),P2(0,y2)點,并且在圖平面上相交于P′點.引導學生利用所學的幾何知識進行計算得到P1,P2點的縱坐標分別為 (1) (2) P′點的坐標為 (3) (4) 綜上所述,根據光路的可逆性原理,當水中的物體斜射入人的眼睛時,即由光密介質斜射入光疏介質的時候,物體的實際位置在人眼看到的像的位置的下方,其水平距離較像與人之間的距離更大,即實際位置在像的右下方. 那從處于水下的潛水艇口觀察空氣中的飛機位置時,像與物的位置關系又是如何呢?此時空氣的折射率即為n1,水的折射率為n2,n2>n1.飛機位于空氣中的P點,人眼從水中觀察到的空氣中的飛機的位置應該位于P′點處.如圖3所示,飛機在P點處發出的光在折射率不同的兩種介質(空氣和水)分界面上會發生折射,單心光束就被破壞成像散光束.同理,讓學生將n1、n2的數值代入(3)、(4)兩式即可得P′點的坐標.根據光路的可逆性原理,當空中的物體斜射入水中人的眼睛時,即由光疏介質斜射入光密介質的時候,物體的實際位置在人眼看到的像的位置的下方,其水平距離較像與人之間的距離更小,即實際位置在像的左下方. 圖3 從水下觀察空中的飛機的光路 那么,垂直入射下的折射成像又是怎樣的呢?[3]在此可以進一步引發學生在上述學習經驗的基礎上,先結合自己所學做出自己的判斷,而后在課堂上師生共同交流、探討最后的答案.對于有認知矛盾的學生,教師就需要去發現學生的問題癥結,并仔細耐心地幫助學生改變原有的認知結構以適應現實情況.在這個過程中,學生個體必須學會順應與調節,以促使自己的認知更加豐富、完善. 此類問題的示圖錯誤經常出現在一些中學物理教輔、教材上,甚至也會出現在不少中學物理教師的板書中.利用建構主義思想,師生通過課堂上的互動發現了這一問題,在共同解決的這一過程中,教師能夠引導學生理性質疑,不盲目相信權威.讓學生知道,知識的應用不應當是簡單的套用,學習知識不能滿足于教條式的掌握,學生在學習過程中還需不斷地領會、把握它在具體情境中的復雜變化.筆者認為在教材編寫中不妨加入相關的反思、拓展閱讀材料,讓師生共同體會、咂摸的同時,又能幫助教師利用建構主義的認知特點合理地設計學生學習的進階.另外,更主要的還在于,對這些知識的思考不僅培養了學生學習幾何光學的興趣,也幫助他們樹立了正確的科學態度和價值觀,擁有思辨性思維.這樣一種對問題追本溯源的方式,既幫助了學生反思自己的學習過程,又幫助了教師在教學領域進一步拓展、深化,具有啟發性. 任何規律的形成都是有條件的,教師在闡述規律時一定要強調該規律在某種特定的情境下適用.讓學生在自己發現問題的過程中創造更多價值.這一過程中,學生有知識的不足、方法的欠缺、想法的不合理,才是教師要教的,也是教師需要去探索如何教的. 對物理問題的研究要透過現象理解其本質,否則容易誤入形式主義的歧途,對物理學的認知也無法達到真正的深入.利用建構主義認知論原理在學生已有的學習經驗基礎上,幫助學生做進一步的拓寬,既符合學生的認知特點也符合教學的循序漸進原則.幫助學生把所學過的相關知識內容整合到一起,豐富他們的認知,梳理他們的知識體系,是值得探索的.學生不應當回避,作為“引路人”的教師更不應該回避.隨著社會科技的發展進步,知識更新加快,新生代教師群體還需不斷更新完善自己的知識體系,做到常有常新,并把這一行為習慣帶給學生,真正做到以身示范,師生遇到問題時也可以共同探討.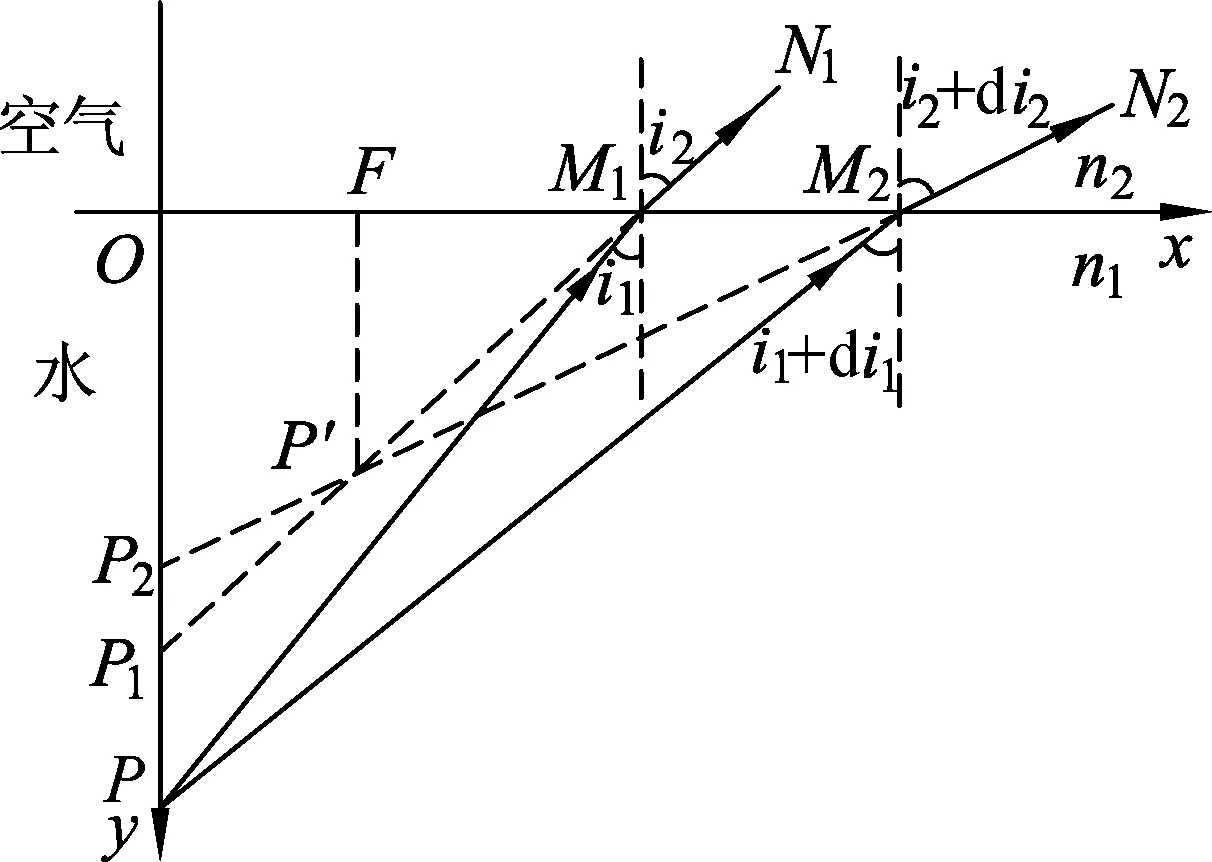
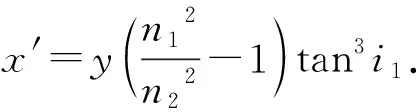
2.4 教學啟示
3 教學反思

