激光跟蹤儀與室內GPS的協同測量組網方法

(航空工業北京長城計量測試技術研究所，北京 100095)

大型裝備制造過程逐步朝著數字化與智能化方向發展，數字化測量技術不僅成為產品設計、加工、制造、裝配及檢測等全生命周期內質量的檢測手段，更成為制造過程狀態監控的主要信息來源，為產品質量提高、制造周期縮短提供有效方法[1-3]。因此，大型裝配制造過程中的測量任務往往具備大尺度、高精度、高效率、高穩定性等特點和需求，僅靠單一系統的測量手段難以滿足[4-7]。以大部件對接任務為例，開始對接過程中要求對接部件位姿的實時監控測量，需要進行多點位高效率的實時監控，不需要太高精度；而在對接最終階段需要對關鍵點位進行高精度測量，其數據為部件的下一步運動提供準確的參數，需要進行高精度的測量[8]。激光跟蹤儀和室內GPS均是新型的數字化測量儀器的代表，若單采用激光跟蹤儀在后期精度可得以保證，但難以完成對接過程的實時監控；若單采用室內GPS可實時監控對接過程，但對接精度則不足[9]。采用激光跟蹤儀和室內GPS組成協同測量網絡，在統一基準的前提下充分發揮兩種系統的優勢，是解決對接這類問題的有效手段[9]。這種利用多種設備協同測量完成同一測量任務的工作模式已成為國內外一大研究熱點[10]。國外，波音公司利用激光跟蹤儀與 V-STARS系統組成協同測量網絡，其中激光跟蹤儀用于進行關鍵控制點的測量，而V-STARS系統以密集點云的形式測量波音787飛機外翼的外形輪廓，為飛機外形裝配準確度檢測和逆向重構提供了數據基礎[11]。在國內，解放軍工程大學的范百興教授研究了激光跟蹤儀與經緯儀的組網方法，在現場獲得了應用[12]；天津大學的邾繼貴教授團隊研究了多站位室內GPS的組網方法，達到了亞毫米的精度[13]。

測量精度是衡量測量網絡性能的重要指標，高精度的組網方法是保證測量精度的有效手段[14]。本文在研究激光跟蹤儀和室內GPS的數學模型基礎上，根據兩種系統的特點，采用了基于傳感單元觀測量的方法構建基本約束方程，為提高整體算法精度，在測量網絡內引入了一維基準尺和三維控制場作為相對約束進行優化，采用了Levenberg-Marquardt 算法進行最優化求解，為保證迭代過程設計了基于后方交匯原理的迭代初值求解方法。最終通過實驗驗證了組網方法的精度優于±0.06 mm，可在工業現場推廣應用。

1 測量原理

1.1 激光跟蹤儀測量原理

激光跟蹤儀是典型的球坐標系測量系統，通過兩個高精度碼盤觀測點位相對于站位的水平角和垂直角，同時通過干涉測距模塊觀測點到站位距離，以極坐標計算的方式唯一確定測量點三維坐標。其測量過程中的坐標系示意圖如圖1所示。

根據水平角φ、垂直角θ和距離r可以唯一確定觀測點P(x,y,z)，可由數學公式表示：

(1)

由任意跟蹤儀坐標系下的測量點坐標P(x,y,z)也可反求水平角φ、垂直角θ和距離r，可由數學公式表示：

(2)

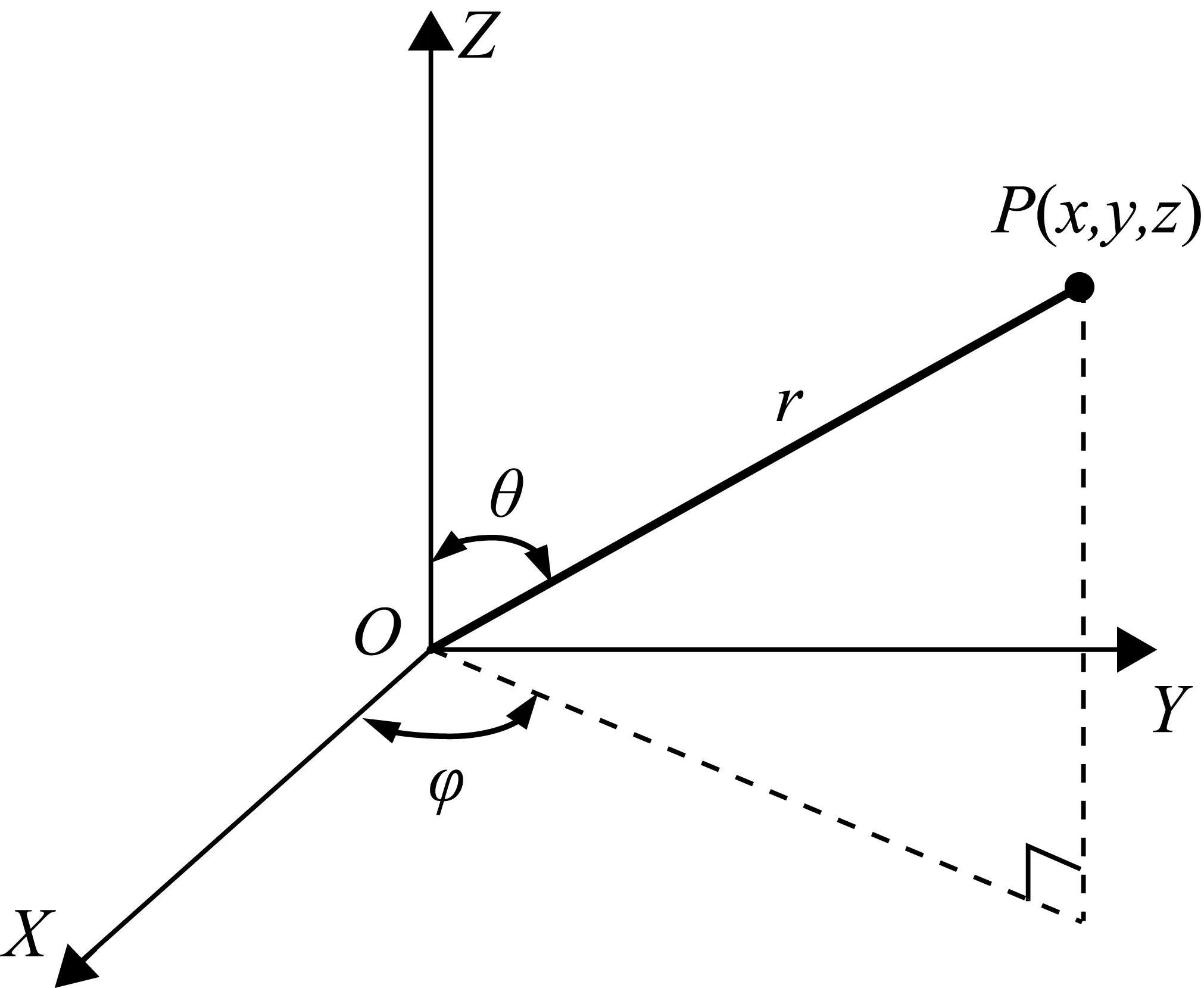
圖1 激光跟蹤儀測量過程中的坐標系示意圖

1.2 室內GPS測量原理

室內GPS是一種基于光電掃描的多站位大尺寸坐標測量系統，系統組成如圖2所示，主要包括：發射站、接收器、信號處理器和解算工作站。發射站發射兩束繞著轉軸勻速旋轉并帶有一定傾斜的激光扇面，在被測空間內實現掃描；接收器感應光信號，并轉化為旋轉角度；信號處理器和解算工作站之間通過無線傳輸模塊進行通信，解算工作站對接收到的時間信息進行處理后進行坐標的解算、顯示及存儲，同時還負責管理整個系統資源，包括現場組網參數以及資源使用權限的分配等。

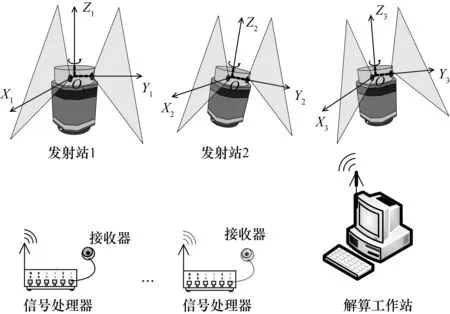
圖2 室內GPS結構示意圖

發射站的結構示意圖和數學模型如圖3所示。發射站主要由轉子和基座組成，轉子帶動兩個線性激光發射器高速繞轉軸旋轉，因此發射站可以抽象為繞著旋轉軸旋轉的兩個非平行激光扇面，激光扇面與旋轉軸間具有一定的傾角，其結構參數即兩激光扇面在發射站坐標系下的方程作為一項重要參數在發射站安裝完成后通過標定精確給定。發射站的數學模型如下：首先，建立發射站坐標系OXYZ，定義旋轉軸為Z軸，激光扇面1和旋轉軸的交點為原點O，激光扇面1上過原點且與旋轉軸垂直的直線為X軸，根據右手定則確定Y軸。發射站逆時針旋轉，發射站兩激光扇面的平面方程為

(3)

式中,(a1,b1,c1,d1)T，(a2,b2,c2,d2)T為預先標定好的光平面1及光平面2的結構參數。

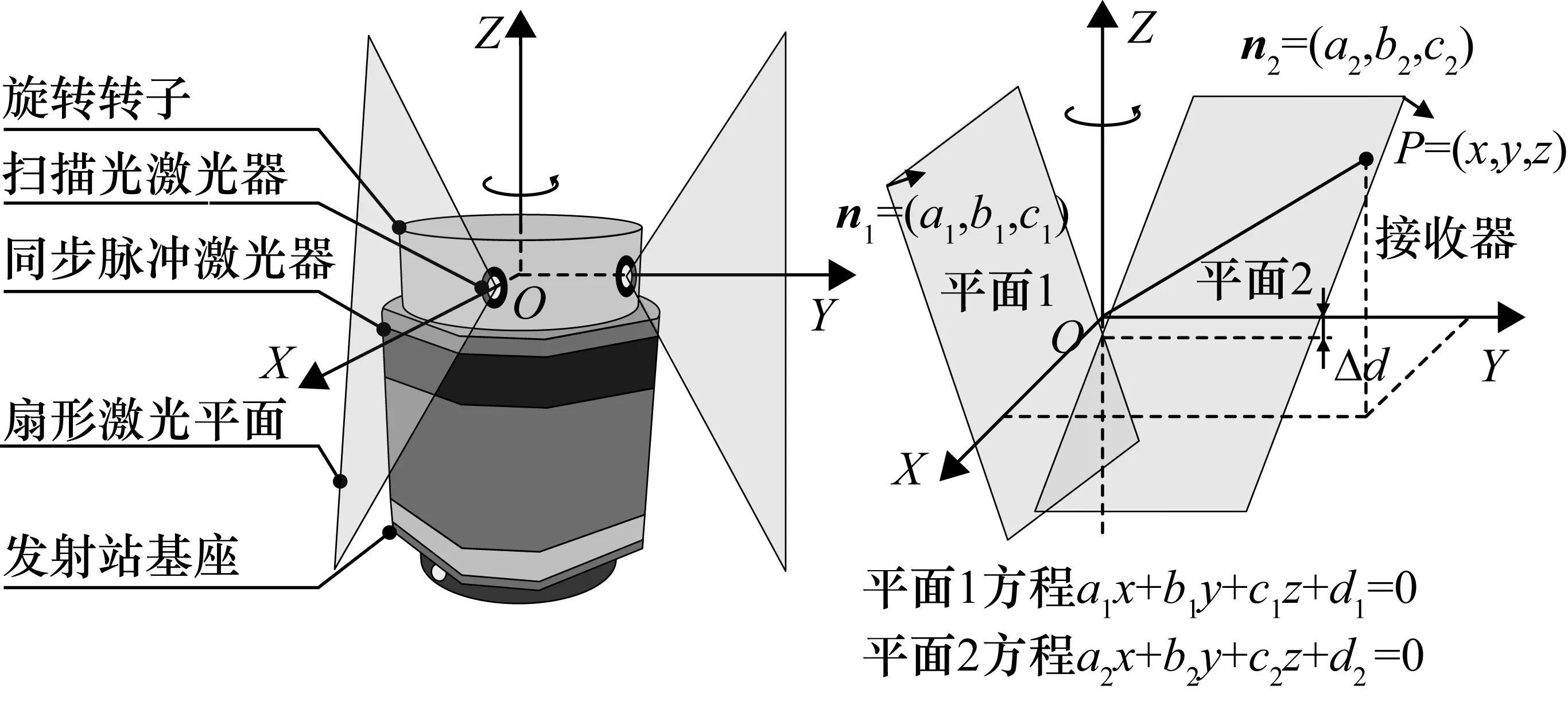
圖3 室內GPS發射站結構及數學模型

當兩激光扇面分別掃過接收器時，可計算光平面旋轉角度θ1,θ2，即掃描角。發射站兩個旋轉激光平面方程在自身坐標系下的方程參數為

(4)

式中,

(5)

(6)

式中，i為發射站編號；j為激光扇面編號；[xkykzk]T為全局坐標系下的待求點三維坐標；Ri和Ti為全局組網定向的結果，它代表全局坐標系到發射站i局部坐標系的轉換關系。

由兩種系統的數學模型可知，儀器站位的位姿關系是測量網絡中的重要參數，而組網的目的就是獲取準確的位姿參數，是測量網絡精度的重要保證。

2 協同組網方法

協同組網問題可具體為測量網絡內具有多臺激光跟蹤儀、多臺室內GPS發射站及若干測量點，通過優化算法實現測量網內所有站位的位姿和所有測量點位的坐標解算，示意圖如圖4所示。為實現兩種系統的協同測量，必須引入相對約束完成組網。為提高算法的精度，采用一維距離約束和三維坐標約束兩種約束構建方法，同時約束方程的構建是依照系統的不同傳感單元進行高度耦合完成。因此，測量網內必須包括基準尺或三維控制場。具體的組網思路是，激光跟蹤儀和室內GPS分別測量基準尺和三維控制場，依照儀器本身測量模型構建基本約束方程，同時通過基準尺的一維距離約束和三維控制場的坐標約束構建相對約束方程，通過迭代優化算法求解由基本方程和相對約束方程構建的最優化方程組，并通過設計合理的迭代初值求解算法完成最終組網。

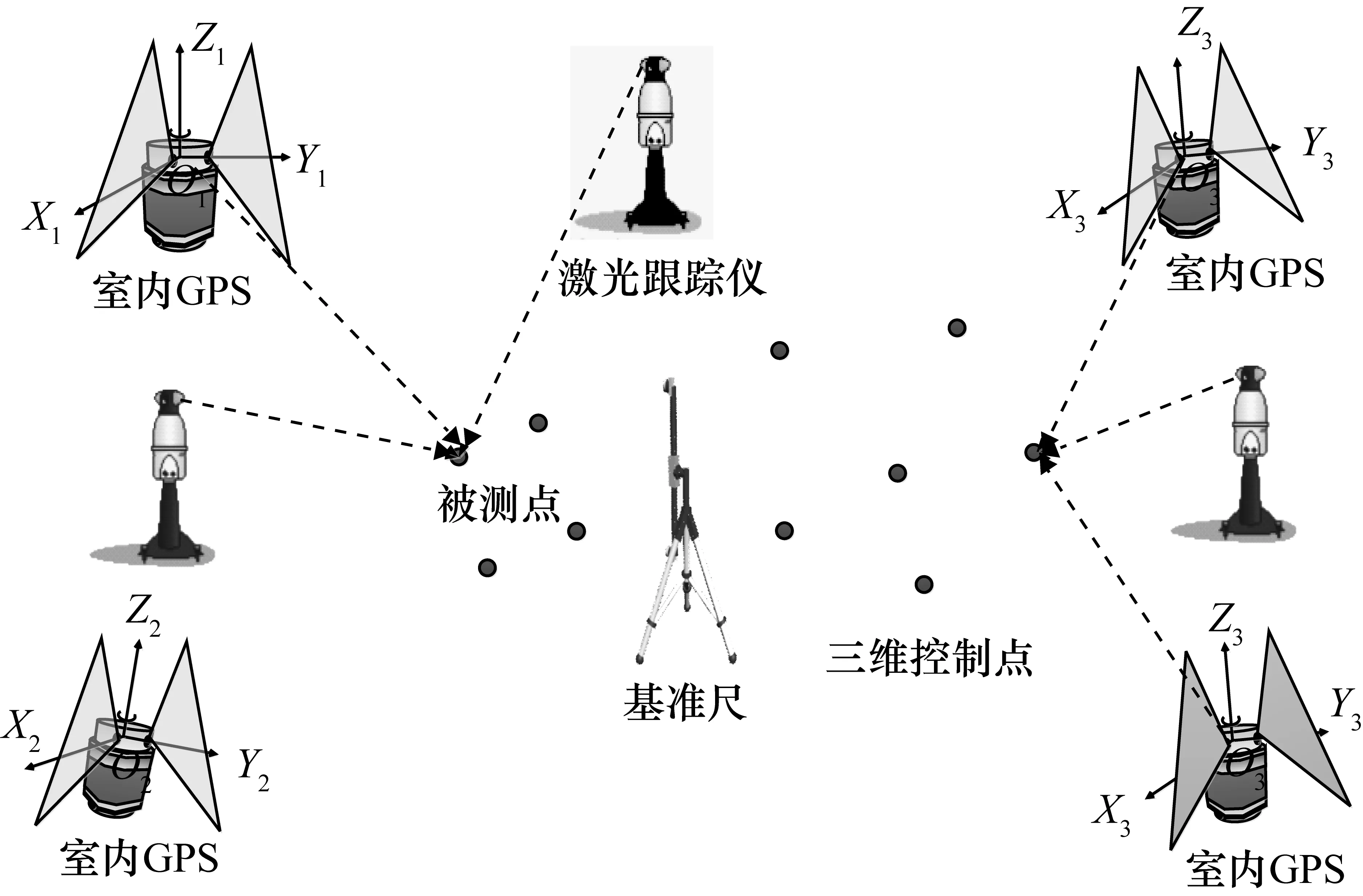
圖4 基于激光跟蹤儀和室內GPS協同組網模型

2.1 協同組網模型

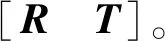
激光跟蹤儀的約束方程可先將控制點轉換到跟蹤儀坐標系下：

(xlaser,ylaser,zlaser)T=Rlaser(xm,ym,zm)T+Tlaser

(7)

式中，(xlaser,ylaser,zlaser)T表示跟蹤儀局部坐標系下的點，代入式(2)中，即可算出對應的觀測量，因此每個跟蹤儀站位可構建以下約束方程：

(8)

式中，帶*標志的是由最終優化點反算回去的觀測值，不帶標志的為儀器觀測值。

室內GPS的約束方程也是同樣將控制點全局坐標轉換到室內GPS局部坐標下：

(xGPS,yGPS,zGPS)T=RGPS(xm,ym,zm)T+TGPS

(9)

結合1.2節中室內GPS數學模型，并依照式(6)，每個室內GPS發射站均可列以下的約束方程：

(10)

協同測量網絡中的一維基準尺是兩端各有測量點同時兩點距離l已知的標準器，因此，可以列以下約束方程：

(11)

求解過程需要達到H1,H2,H3共3組約束方程的最優結果，可以采用罰函數法構造以下最優化函數求解：

(12)

式中，λ1,λ2代表懲罰因子。每臺儀器均有3個未知參量，共有3(I+J)個未知量。每個點位均可有3個跟蹤儀方程，2個室內GPS方程；每個基準尺有一個距離約束方程。因此，總共約束方程的個數為：3IM+2JM+K。當方程數大于未知量數，即滿足3IM+2JM+K>3(I+J)時，可采用Levenberg-Marquardt算法進行求解，得到每個站位的位姿參數，完成組網[15]。

2.2 迭代初值求解方法

Levenberg-Marquardt算法是一種兼具梯度法和牛頓法的優點的非線性最小二乘算法，其收斂速度快、穩定性好[16-18]。但是，采用Levenberg-Marquardt算法必須采用合適的迭代初值，否則易造成迭代不收斂而影響算法精度和速率。算法中的迭代初值主要包括激光跟蹤儀和室內GPS每個站位初始的位姿參數。其中激光跟蹤儀可直接進行點位測量，可通過多點的坐標系轉換方法完成迭代初值獲取[19]。室內GPS是多站位系統，只有角度觀測值，需要采用一種基于后方交匯的迭代初值計算方法，依據系統局部坐標系與全局坐標系的點一一對應并且對應點的連接射線交匯于一點來構建約束方程[20]，示意圖如圖5所示。測量系統局部坐標系下的點a，b，c與全局坐標系下的A，B，C是一一對應關系，其連線交匯于空間點S，可利用這一約束完成迭代初值求解。考慮到每個發射站的初值獲取方式一致，下面以單發射站為例闡述迭代初值估計過程。

圖5 基于后方交匯方法的迭代初值計算方法

根據數學模型，約束方程可以寫成以下矩陣形式：

AX=0

(13)

其中，

是一個2m×12的系數矩陣。

作為未知參數， 將未知量X分解為

則方程可表示為

BX9+CX3=0

(14)

根據正交矩陣的特性‖X3‖2=1，最優化方程可寫為

CR=‖BX9+CX3‖2+λ(‖X3‖2-1)

(15)

式中，λ為任意實數，將方程展開可以得到：

(16)

分別求CR求X9和X3的偏導函數，偏導函數值為0，方程為

(17)

將方程組化簡為

(18)

式中,D=CTC-CTB(BTB)-1BTC，是個3×3的矩陣。X3是矩陣D的特征向量，從而可以解出X3，將X3帶入第二方程即可解出X9，從而得到迭代初值。將迭代初值帶入最終優化方程完成組網。

3 實驗

為驗證協同組網方法的性能和精度，在工業現場某廠房設計了以下實驗。該實驗面向工業現場條件下某部件模擬對接的任務中的組網過程，考慮現場條件，采用激光跟蹤儀AT402和室內GPS組成協同測量網絡，利用第2節的方法優化解算所有激光跟蹤儀和室內GPS的站位位姿，可利用激光跟蹤儀完成關鍵點位測量，室內GPS完成部件實時跟蹤測量，實現兩種儀器統一基準下的精確測量，可完成測量任務中的所有功能要求。實驗現場如圖6所示，實驗中采用一臺激光跟蹤儀和兩臺室內GPS發射站組成協同測量網絡，并利用基準尺進行精度驗證。

圖6 現場條件下協同測量實驗圖

為了驗證激光跟蹤儀和室內GPS協同測量網絡的精度，在12 m×12 m×2 m的工作區域內隨機布置10根基準尺，要求基準尺包含水平豎直縱深各個方向，基準尺兩端的距離參量作為標準值，通過測量基準尺兩端點位坐標算出距離值，該距離值與標準值進行比較，以差值大小作為評價網絡精度優劣的標準。具體比對結果如圖7所示。

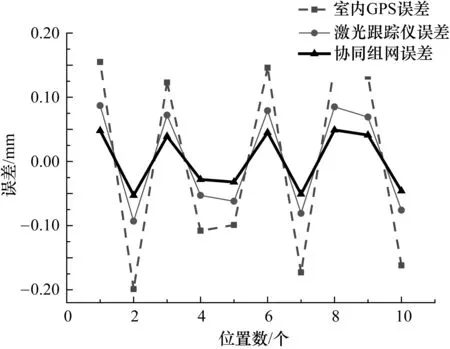
圖7 精度對比結果

圖7中包括3組數據，其中虛線代表單采用室內GPS測量的比對結果,細實線代表單采用激光跟蹤儀的比對結果,粗實線代表室內GPS與激光跟蹤儀協同測量的比對結果，以上的結果均針對同一測量對象。由實驗數據可以看出，單采用室內GPS測量誤差優于±0.200 mm，單采用激光跟蹤儀的測量誤差優于±0.100 mm，采用協同測量手段的結果優于以上兩種方法，數據顯示其測量誤差優于±0.06 mm。數據證明了協同組網的方法能夠提高網絡測量的精度，具有高精度和高效率的優點。

4 結束語

針對單一系統在測量范圍、精度和效率上難以滿足現場需求的問題，采用一種基于激光跟蹤儀與室內GPS的協同測量方法。在研究兩種系統的數學原理前提下，提出了一種基于兩種儀器不同傳感單元的約束方程組構建方案，同時為提高網絡的整體精度，在空間內引入了一維基準尺和三維控制場，以一維基準尺的距離和三維控制場的坐標作為相對約束構建方程，形成了最終帶有懲罰因子的罰函數最優化方程。采用了基于后方交匯原理的迭代初值獲取方法，使用Levenberg-Marquardt算法完成求解，最終實現了激光跟蹤儀與室內GPS的協同測量。使得測量網絡具備了激光跟蹤儀的高精度和室內GPS的高效率的特點，實驗數據表明協同網絡的精度優于±0.06 mm，證明了組網方法的精度，具備較大的推廣價值。值得注意的是，測量網絡中激光跟蹤儀和室內GPS站位的布局也會影響組網精度，在未來可通過研究布局優化算法進一步提高測量網絡精度。