基于平均差異度的改進k-prototypes聚類算法*

石鴻雁， 徐明明

(沈陽工業(yè)大學 理學院， 沈陽 110870)

聚類是將物理或者抽象的對象集合分成若干個類，使得同一個類中的對象具有較高相似度，不同類中的對象具有較低相似度[1]，聚類分析技術在圖像處理、模式識別、生物學等諸多領域有著廣泛的應用[2-4].在實際生活中的各個方面比如醫(yī)療衛(wèi)生教育、社交網站、商場和購物網站等領域每時每刻都會產生大量的數據，這些數據大多是由連續(xù)的數值屬性和代表類別的分類屬性所構成的混合屬性數據，所以混合屬性數據聚類算法的研究成為聚類分析領域的一個熱點問題.目前，許多學者對混合屬性數據聚類進行研究，并提出了一些相關算法.Huang結合k-means和k-modes算法的思想提出了k-prototypes算法[5]，該算法實現簡單，易操作，能夠有效聚類混合數據，但其對初始聚類中心和聚類數目過于依賴，使得聚類結果容易陷入局部最優(yōu)，并且在計算分類屬性之間的相異度時，簡單采用數值0和1不能客觀地體現數據對象與類之間的相異度，從而導致聚類結果不理想.針對k-prototypes算法存在的問題，歐陽浩等提出了基于信息熵的粗糙k-prototypes聚類算法[6]，利用信息熵的概念，為每個數據對象的分類屬性賦予權重，并且引入粗糙集的理論來計算各數據對象與粗糙中心之間的差異度，提高了聚類結果的準確率.Chatzis提出了一種新的FCM算法[7]，對Gath-Geva算法進行了擴展，該算法假設簇中的數據對象符合高斯分布，主要對高斯多項分布數據進行聚類.Zheng等利用進化算法(EA)具有全局搜索能力的特點，將其引入到k-prototypes算法中，提出EKP算法[8]，算法中令k-prototypes算法作為局部搜索策略，并在EA框架的控制下運行.錢潮愷等[9]針對k-prototypes算法分辨率低，聚類結果的隨機性較大等問題，提出基于維度頻率相異度的方法來計算分類屬性，并且對預聚類產生的子簇構造連通圖，分析其之間的連通關系，用強連通融合方法進行聚類.陳晉音等提出了基于混合屬性距離度量公式的密度聚類算法[10]，將數據對象分為分類占優(yōu)、數值占優(yōu)和均衡型，對于不同情況的特征，分別選擇不同的距離度量方式，通過預先設定的參數尋找數據密度最大的區(qū)域，選定核心點，再根據核心點將密度相連的數據對象劃分為一類，最后得到聚類結果.

上述處理混合屬性數據的算法雖然在不同程度上提高了聚類效果，但大都采取了隨機選擇初始聚類中心的方式，給算法的執(zhí)行效率帶來了很大的不確定性[11].為了解決這個問題，已有學者提出一些改進算法，文獻[12]在考慮數據對象在類歸屬上不確定的同時，利用均值和分布質心表示類中心；文獻[13]提出了基于密度聚類中心自動確定的聚類算法.實際上，聚類中心點的分布比較疏散，不會局限在一個小的范圍區(qū)域內.本文利用平均差異度方法選取初始聚類中心點，并用這些點進行聚類，可以得到較好的效果.為進一步提高算法質量，利用信息熵確定數值屬性權重，并對分類屬性度量公式進行改進，給出了一種混合屬性數據度量公式.

1 k-prototypes聚類算法

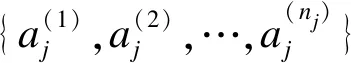
設k∈N+，k-prototypes算法聚類是將數據集劃分成k個不同的類，使得目標函數值最小，即

(1)

式中：vl為類cl的聚類中心，cl為聚類集；μil為數據對象xi對類cl的隸屬度，0≤μil≤1；d(xi，vl)為混合屬性數據度量公式，即

(2)

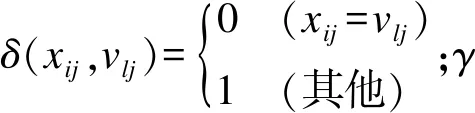
1) 在數據集中任選k個初始聚類中心點；

2) 根據式(2)計算對象與初始聚類中心的距離，按照最小距離原則分到離其最近的中心所在的類中；

3) 更新聚類中心，對數值屬性數據求平均值，對分類屬性數據求屬性中出現次數最多的值；

4) 重復步驟2)和3)，直到目標函數F不再發(fā)生變化為止.

2 改進k-prototypes聚類算法

k-prototypes算法雖實現了混合屬性數據的有效聚類，但在聚類過程中仍存在一些問題，隨機選取初始聚類中心導致聚類結果具有不確定性和隨機性.采用式(2)計算數據對象間的相似度，忽略了數值屬性數據對聚類結果的影響.同時分類屬性采用簡單匹配度量計算數據與類中心的相似度有兩個缺點：1)不能準確地描述數據對象與類中心對應的簇中其他數據的相似度，數據對象是否被劃分到一個簇中，不僅依賴于與聚類中心的相似度，還依賴于與類內已有對象的總體相似度；2)當數據對象與多個聚類中心的相似度相同時，算法往往會隨機將此數據加入到一個聚類集中，從而不能準確地劃分到相似性更大的聚類集中.

2.1 改進的混合屬性數據度量公式

針對k-prototypes算法存在的問題，利用信息熵Ej的概念對數值屬性進行加權，并對分類屬性度量公式進行改進，給出混合屬性數據度量公式.

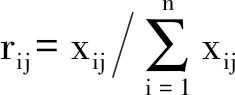
(3)

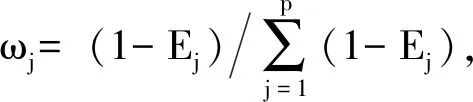
定義1數值屬性度量采用加權曼哈頓距離公式，數據對象xi與xj之間的度量計算定義為

(4)

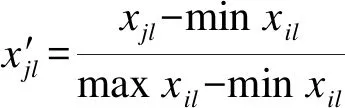
定義2設cl表示聚類過程中的一個類，則分類屬性度量公式定義為

(5)

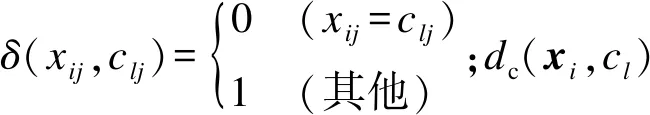
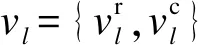
(6)

將定義3應用到k-prototypes算法的目標函數中，即

(7)

2.2 初始聚類中心選取

為了克服隨機選擇初始聚類中心導致聚類結果不穩(wěn)定的問題，借鑒文獻[15]中選擇初始聚類中心點的思想，并且利用平均差異度選取初始聚類中心.基于的原則是：初始聚類中心應具有較大的平均差異度，且聚類中心之間的差異度要大于總體平均差異度.

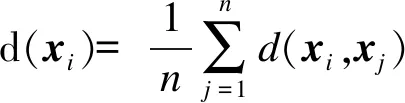
平均差異度的計算依賴于數據對象兩兩之間的距離d(xi，xj)，本文采用混合屬性數據距離代替原方法中的歐式距離，其中數值部分為由定義1給出的數值屬性度量公式，分類屬性部分采用簡單匹配度量，從而擴展了原方法只能處理數值屬性數據的限制，使其能夠更好地解決混合屬性數據聚類問題.

2.3 算法描述

綜上得到基于平均差異度的改進k-prototypes聚類算法的步驟如下：

1) 給定聚類個數k，計算每個數據對象的平均差異度和總體平均差異度，將平均差異度進行排序，并把平均差異度最大的數據對象作為第1個初始聚類中心v1，同時將該數據從數據集中刪除；

2) 尋找其余數據對象中平均差異度最大的數據，計算其與已有聚類中心的距離；

3) 若計算其與已有聚類中心的距離均不小于總體平均差異度，則可作為聚類中心，否則，返回步驟2)，重復步驟2)和3)，直到初始聚類中心的個數達到k，并輸出初始聚類中心；

4) 根據定義3計算數據對象到各聚類集的距離，按照就近原則將數據分配到離其最近的聚類集中；

5) 更新每個類的中心，對數值屬性數據計算平均值，對分類屬性數據取屬性中出現概率最大的值；

6) 重復步驟4)和5)，直到各個聚類中心穩(wěn)定，目標函數值不再發(fā)生變化，結束.

3 仿真試驗與結果分析

3.1 試驗環(huán)境

本文仿真試驗采用Matlab R2012a開發(fā)環(huán)境，Intel(R) Core(TM) i3-4005U CPU 1.70 GHz，4 GB內存，在Windows7操作系統(tǒng)上運行.試驗數據采用UCI機器學習數據庫中的4個真實數據集，數據集描述如表1所示.

表1 試驗數據集描述Tab.1 Description of experiment data sets

以上4個數據集包括3種數據類型，其中Iris為數值型數據，Soybean為分類型數據，Credit和Heart為混合型數據.

3.2 試驗結果

為了驗證本文算法的有效性和可行性，分別用k-prototypes算法、EKP算法、KL-FCM-GM算法、文獻[12]算法、文獻[13]算法和本文算法對上述數據進行聚類分析，試驗結果如圖1所示.

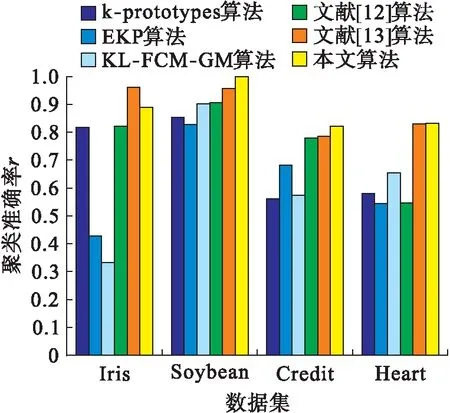
圖1 各種算法的聚類準確率Fig.1 Clustering accuracy of various algorithms

從圖1可以看出，本文算法在處理Soybean數據集、Credit數據集和Heart數據集時，聚類準確率都高于其他算法，只有在處理Iris數據時，低于文獻[13]算法，但優(yōu)于其他算法.這說明本文算法在處理混合型數據和分類型數據時有效性更高，而處理數值型數據有待提高.

為了進一步驗證本文算法的聚類質量，比較本文算法與k-prototypes算法的聚類精度，利用Credit數據集的聚類結果，根據數據集依次迭代不同次數所對應的目標函數值，生成的對比結果如圖2所示.

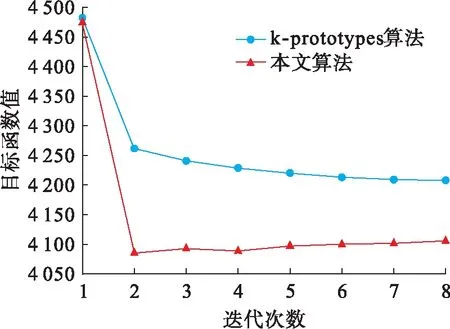
圖2 迭代次數與目標函數曲線Fig.2 Curves of iteration number and objective function

從圖2可以看出，目標函數值均隨著迭代次數的增高而降低，但是在相同條件下，本文算法的目標函數值比k-prototypes算法低，說明本文算法的聚類精度比k-prototypes算法高.

3.3 算法復雜度分析

本文算法主要由初始聚類中心的選取和聚類迭代兩部分構成，其中選取初始聚類中心要計算數據對象之間的距離和尋找聚類中心，該過程的計算代價分別為O(n2)和O(kn)，確定聚類中心后，算法需要進行迭代劃分，其計算代價為O(tkn)，因此，總的時間復雜度變?yōu)镺(n2+kn+tkn)，其中，t為迭代次數，k?n.本文算法和其他算法的時間復雜度比較如表2所示.

表2 算法的時間復雜度統(tǒng)計Tab.2 Statistics results of time complexity for various algorithms

從表2中分析可以得出，本文算法的時間復雜度比k-prototypes、EKP、KL-FCM-GM及文獻[12]要高，主要消耗在選取初始聚類中心的環(huán)節(jié)上，但是確定了較優(yōu)的聚類中心點之后，會減少迭代次數，并得到較滿意的聚類結果，從而在一定程度上可以彌補時間復雜度較高的不足.

4 結 論

本文提出的基于平均差異度的改進k-prototypes聚類算法，是在傳統(tǒng)k-prototypes聚類算法基礎上進行的擴展.通過利用平均差異度確定初始聚類中心，考慮了數據的空間分布信息，使得聚類中心更符合實際情況，避免了對初始中心選擇所帶來的不確定性.改進的分類屬性數據度量公式，不僅考慮了數據對象與類中心的距離，還有效利用了數據與類中已有對象之間的總體相異性，使得在迭代過程中，對聚類集中已有對象的信息進行了統(tǒng)計參考，從而獲得更好的聚類結果.但該算法中聚類數目的選擇會影響聚類結果，因此，下一步將研究聚類數目的確定方法，尋找能夠自動選取合理聚類數目的方法.