車聯網蠕蟲的隨機傳播模型*
周翰遜,楊 陽,馮潤澤,熊俊坤,萬 明,郭 薇
1.遼寧大學 信息學院,沈陽 110036
2.沈陽航空航天大學 計算機學院,沈陽 110136
1 引言
隨著信息技術的不斷發展以及數據量的激增,人們迫切地需要將客觀世界的物體與網絡相連,因此產生了物聯網產業[1-3]。自從物聯網納入到國家十二五規劃中,物聯網技術得到了國家的大力扶持也得到了迅猛的發展。作為物聯網的重要領域——車聯網也得到了學術界以及商業界的重視[4]。目前,百度、阿里巴巴、騰訊等公司已經推出了車聯網相關產品。然而,在車聯網得到蓬勃發展的同時,人們對于車聯網中的安全問題也越來越關注。一旦車聯網遭到惡意攻擊,將會給人和車輛的安全造成嚴重威脅。
車聯網蠕蟲作為車聯網的重要安全問題之一,也引起人們廣泛關注。由于構建網絡蠕蟲的傳播模型可以揭示其傳播的內在規律[5-9],因此人們試圖對其進行數學建模。文獻[10]首次對于在高速公路傳播的網絡蠕蟲進行了分析。然而,該方法不能考慮V2V(vehicle-to-vehicle)的動態特性并且高估了網絡蠕蟲在高速公路中的傳播速度[11]。文獻[12]提出了影響蠕蟲在道路上傳播的重要參數,即通信范圍、車輛密度以及介質訪問控制機制等。文獻[13]研究了蠕蟲在大規模道路網絡中的傳播動態特性,并且發現蠕蟲可以在幾分鐘內就感染大量道路上具有漏洞的車輛。然而,如上工作只是通過仿真工具研究了網絡蠕蟲在車聯網中的傳播特性,并沒有提出準確的數學模型對車聯網中的蠕蟲傳播進行建模。
本文基于隨機過程理論對車聯網中蠕蟲的傳播進行了數學建模。在沒有安全防護軟件的理想情況下,基于Galton-Watson 分支過程對車聯網蠕蟲進行了建模;在具有安全防護軟件的現實情況下,當高速公路車流符合泊松分布時,基于排隊論對車聯網蠕蟲進行了建模,并且研究了其穩定性條件。當高速公路車流符合正態分布時,基于馬爾可夫鏈對車聯網蠕蟲進行了建模。最后,通過仿真實驗驗證了提出的車聯網蠕蟲傳播模型。
2 車聯網蠕蟲
車聯網蠕蟲是指利用車載計算機及其他電子設備嵌入式平臺存在的安全漏洞而在車聯網中傳播的網絡蠕蟲,對于在車聯網中的車輛安全駕駛構成嚴重的威脅。目前的車聯網可以劃分為V2V 和V2I(vehicle-to-infrastructure)兩種形式[8]。V2V是指車與車之間可以互相通信,能夠讓相互靠近的汽車之間互相發送諸如位置、速度以及行駛方向等基本的安全信息,從而大大減少汽車碰撞事故的發生概率并緩解交通擁堵。V2I 是指汽車與道路基礎設施進行通信,汽車可以通過道路基礎設施交換道路基本信息,甚至連接其他網絡。由于V2I不容易受到攻擊[8],因此本文主要研究V2V下的車聯網蠕蟲的傳播規律。
經典的網絡蠕蟲如掃描蠕蟲,可以在短時間內感染全世界接入互聯網的具有該蠕蟲可以感染的所有漏洞主機,但是由于目前V2V 通信的最大范圍為300 m,因此車聯網網絡蠕蟲只能感染離感染車輛最大范圍為300 m 內的車輛。在車聯網中,由于諸如SAE J2735 等V2V 通信標準均支持在高頻段中周期性廣播信標消息,因此車聯網蠕蟲可以很容易地收集車輛的相關信息并且找到具有漏洞的車輛進行攻擊。車聯網蠕蟲的攻擊策略可以劃分為攻擊所有的漏洞車輛,或者為了避免被人們發現選擇性地攻擊傳播范圍內的一輛漏洞車輛兩種。圖1 為車聯網蠕蟲選擇性攻擊一輛漏洞車輛的攻擊示意圖。車A攻擊具有漏洞的車B成功后,車B又對于具有漏洞的車輛C進行攻擊,以此類推,完成車聯網蠕蟲的攻擊過程。
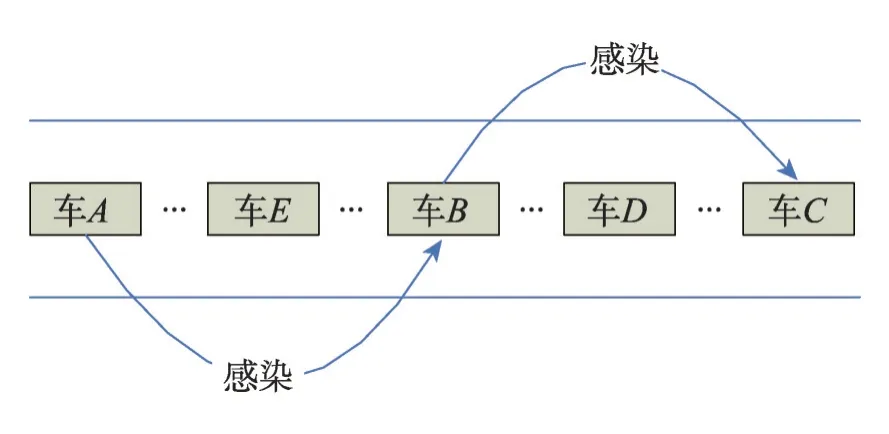
Fig.1 Worm propagation in Internet of vehicles圖1 車聯網蠕蟲的傳播
3 車聯網蠕蟲的隨機傳播模型
3.1 車流模型
在討論車聯網蠕蟲傳播模型前,先討論公路上的車流模型。首先,考慮單車道的車流模型。假設在單位時間車輛的到達概率為p,具有蠕蟲可以感染的漏洞車輛率為r時,在單位時間內到達具有蠕蟲可以感染的漏洞車輛為k的概率為:

其中,n為V2V 通信的最大范圍內容納的車輛數。由于目前V2V通信的最大范圍為300 m,汽車的最短車長3 m,因此在單車道300 m 的范圍內最大容納的車輛數為100 輛。由于國內標準城市干道每條機動車道3.5 m,因此300 m 的范圍內可以有85 條車道。如果有j條車道,那么V2V 通信的最大范圍內容納的車輛數n為100×j,j≤85。
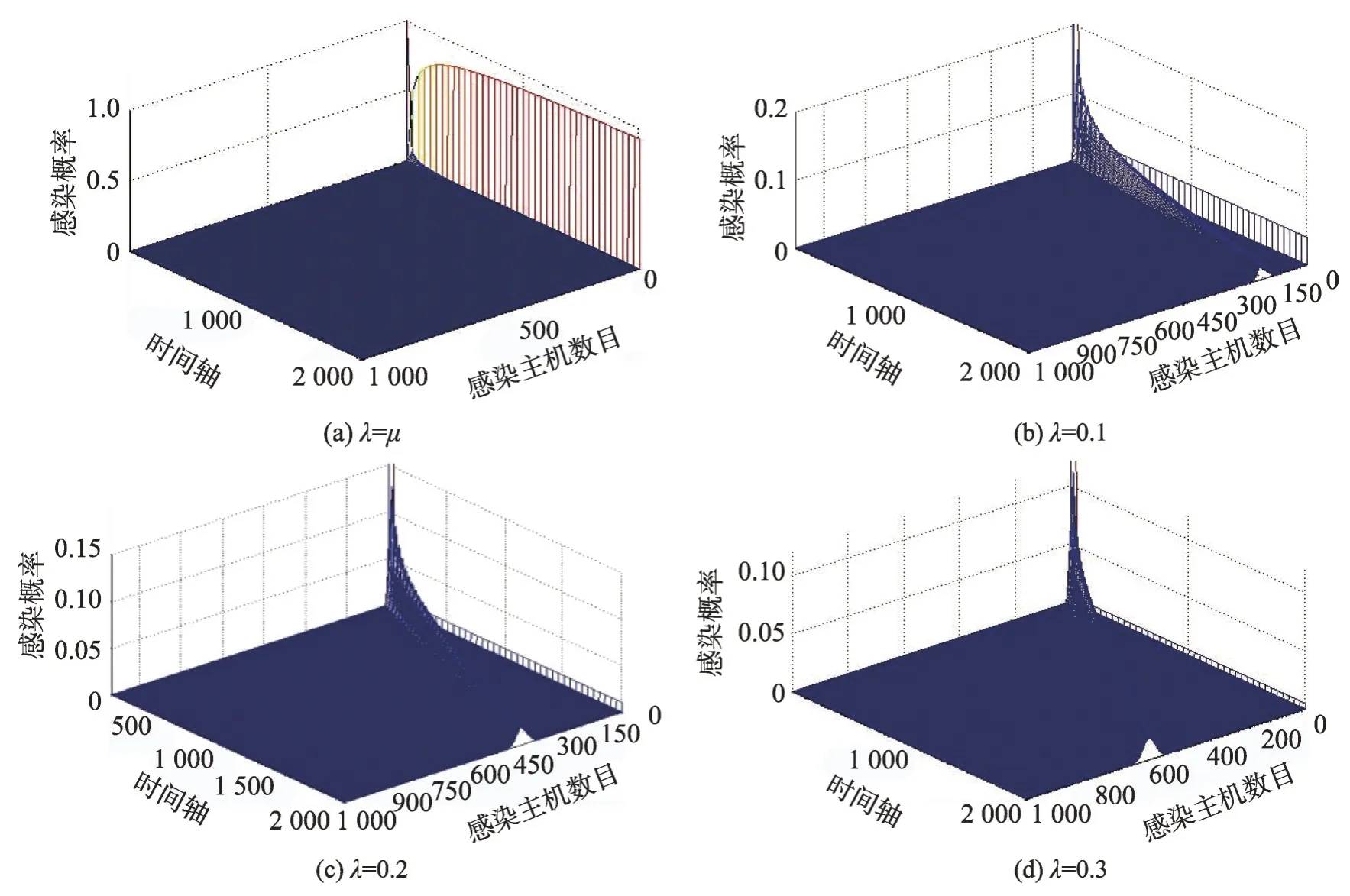
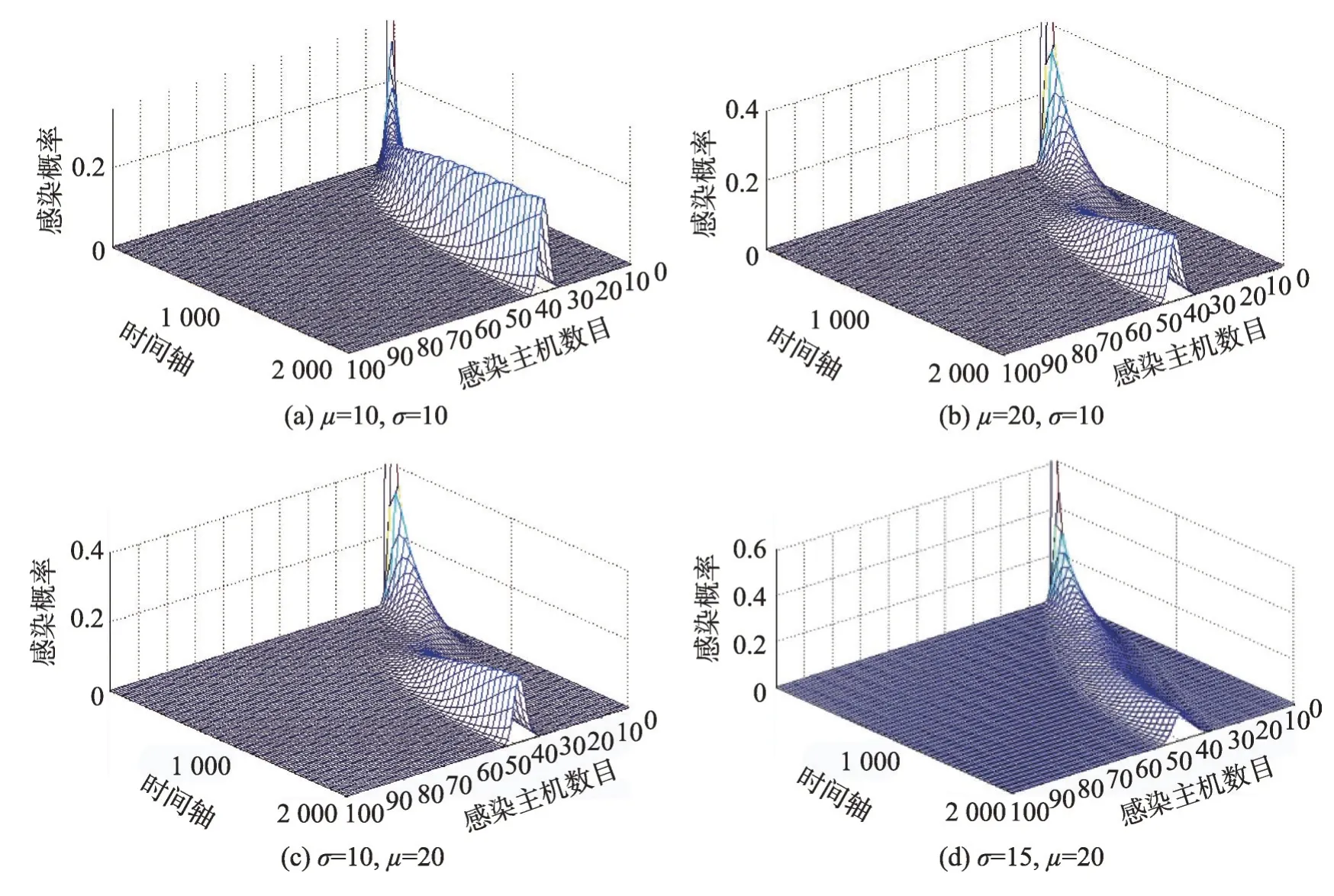
當車輛到達概率較小時(可以近似看作車輛的平均流速較小),也就是p×r較小時(0 然而,由于不同國家人們駕車習慣或者文化的不同,車流的模型可能會有所差異[14]。文獻[14-15]對上海的高速公路上的車流進行分析,發現其更符合正態分布: 其中,μ為車流平均值,σ2為車流的方差。 下面研究i個車道的具有蠕蟲可以感染的漏洞車流模型,若車流中具有蠕蟲可以感染的漏洞車輛率為r,那么在i條車道中,單位時間內到達的漏洞車輛數X: 因此,X~N(p×(r×100×i),(r×100×i)2σ2)。 如果感染車輛攻擊全部漏洞車輛,那么其符合上文所述的泊松或者高斯分布;如果感染車輛選擇性攻擊一輛車輛,那么其符合0-1分布,如下: 其中,p為漏洞車輛大于等于1 的概率(無論車流符合泊松或者高斯分布,都可以很容易計算該概率0 由于車聯網對于安全威脅,尤其是車體客戶端蠕蟲的安全威脅的處理機制并不成熟[8],而且蠕蟲在車聯網中傳播得又相當快,因此本節主要研究在沒有蠕蟲查殺的情況下,車聯網蠕蟲的隨機傳播模型。車聯網蠕蟲可以感染的車輛可以劃分為感染類和易感類。其中,易感類為車聯網蠕蟲可以感染的具有漏洞的車輛,感染類為已經被車聯網蠕蟲感染的車輛。車聯網中跟蠕蟲傳播相關的車輛只能處于感染類或者易感類,易感類可以被車聯網蠕蟲感染而轉化為感染類主機。 3.2.1 基于Galton-Watson 分支過程的車聯網蠕蟲傳播模型 Galton-Watson分支過程描述第n代個體獨立同分布的感染第n+1 代個體的數學模型。在車聯網蠕蟲的傳播過程中,在車聯網中首先植入的蠕蟲為第0代車聯網蠕蟲,其直接感染的車聯網蠕蟲為第1代車聯網蠕蟲。以此類推,第n代車聯網蠕蟲可以感染第n+1 代車聯網蠕蟲,由于每代蠕蟲獨立地感染下一代的蠕蟲,因此其感染具有獨立性。通過3.1節的討論,假設車聯網蠕蟲可以感染300 m內的所有漏洞車輛(3.3 節討論僅感染300 m 內的一輛漏洞車輛),因此第n代蠕蟲感染第n+1 代蠕蟲數目服從均值和方差均與車流相關的泊松或者高斯分布。雖然車流在一天的時間里是變化的,但是由于車聯網蠕蟲的傳播時間相當快,如10 min。因此在如此短的時間內,可以近似車流為恒定不變的,車聯網蠕蟲的第n代感染第n+1 代蠕蟲數目服從同分布。又由于車聯網蠕蟲的感染是獨立感染不進行互相協作,因此車聯網蠕蟲的第n代個體獨立同分布地感染第n+1 代個體,因此其符合Galton-Watson分支過程。 令Yn為車聯網蠕蟲傳播到了第n代,Y0為車聯網蠕蟲最初的感染主機數目。由于在車聯網蠕蟲傳播的過程中,每代蠕蟲感染其下一代是相互獨立的,并且具有相同的概率分布。第n代新感染的主機為第n+1 代,令為在第n代中被感染的第k個主根據不同路況情機,那么第n+1 代主機況服從泊松分布或者高斯分布。由此可知,只要給定Yn,那么Yn+1的分布就完全決定了,且與以前的Yn-1,Yn-2…無關,故{Yn,n≥1}也是一個馬氏鏈。定理1給出了其狀態轉移概率的計算方法。 定理1車聯網蠕蟲的Galton-Watson 分支過程{Yn:n=0,1,…}的一步轉移概率矩陣為: 其中: 證明設F(s)是隨機變量Yn的母函數,母函數的定義為: 由于車聯網蠕蟲感染的后代車輛數目服從的概率分布密度已知,因此很容易得到相應的概率分布為: 又由于母函數有如下性質:(1)Y的母函數與其分布率是一一對應的,且有;(2)設非負整值隨機變量Y1,Y2,…,Yn相互獨立,而g1,g2,…,gn分別是它們的母函數,則的母函數為:gY(s)=g1(s)g2(s)…gn(s)。因此,將其概率母函數帶入式(6)得: 因此,可以得到如下等式(10): 由于當i=0 時pij=ρ0,j,因此定理得到了證明。 □ 從定理1 中不難發現:p00=1,p0k=0(k>0)。因此,狀態0 是車聯網蠕蟲的Galton-Watson 分支過程的吸收狀態。在車聯網蠕蟲的分支過程模型中,最關心的問題是此過程被狀態0吸收的概率,即滅絕概率問題。下個小節將詳細討論。 3.2.2 滅絕概率 對于車聯網蠕蟲的Galton-Watson 分支過程模型,滅絕概率P{Yn→0}即對于過程{Yn,n=0,1,…},給定Y0=1 時,第n代有0 個車聯網蠕蟲的概率=P{Yn=0|Y0=1}的極限。 定理2若車聯網蠕蟲傳播的分支過程為對于攻擊傳播范圍內所有的漏洞車輛的車聯網蠕蟲,其滅絕概率為1,當且僅當r×300×i×p≤1;對于選擇性地攻擊傳播范圍內的一輛漏洞車輛的車聯網蠕蟲,其滅絕概率為1,即必將滅亡。 證明令車聯網蠕蟲感染后代的均值為若Y0=1,下面計算E(Yn)和Var(Yn)。首先,可以寫出,Yi表示第n-1代車聯網蠕蟲的第i個蠕蟲感染后代的個數。因此: 其中,E[Yi]=μ。由于E[Y0]=1,由式(11)可以得到如下結論: 如果以π0記總體最終的滅絕概率,因此: 若μ<1,則π0=1。這是因為: 由于當μ<1時μn→0,因此P(Yn≥1)→0,P(Yn=0)→1,即π0=1。同理,很容易證明當μ=1 時,π0=1。 如果車聯網蠕蟲攻擊傳播范圍內的所有漏洞車輛,無論車流符合泊松還是高斯分布,其均值μ都為r×300×i×p,因此r×300×i×p≤1;對于選擇性地攻擊傳播范圍內的一輛漏洞車輛的車聯網蠕蟲,由于每代車聯網蠕蟲的傳播符合0-1 分布,其均值μ為p,而且0 從定理2 中不難發現如果車聯網蠕蟲選擇性地攻擊傳播范圍內的一輛漏洞車輛,其必將滅亡,這違背了蠕蟲攻擊的初衷,因此車聯網蠕蟲選擇攻擊傳播范圍內的所有漏洞車輛的意義更大。從定理2 可知,選擇攻擊傳播范圍內的所有漏洞車輛的車聯網蠕蟲滅絕的充要條件為p≤1/(r×300×i)。由于車流p,V2V 的傳播范圍為300 m 以及車道數目i都是無法人為干預的,因此人們只能通過將具有漏洞的車輛進行打補丁降低漏洞率r,才能使得車聯網蠕蟲最終滅絕。從定理2也可以得知,無論車流服從泊松分布還是高斯分布,其滅絕概率與其分布沒有關系。由于選擇性地攻擊傳播范圍內的一輛漏洞車輛的攻擊策略終將滅絕,因此下面主要討論選擇攻擊傳播范圍內的所有漏洞車輛的車聯網蠕蟲。 由于沒有考慮人們對于蠕蟲查殺的情況,因此車聯網蠕蟲的Galton-Watson分支過程模型可以準確地描述車聯網蠕蟲傳播初期或者當車聯網由于發展不完善缺乏對于車聯網蠕蟲查殺的軟件情況。然而,隨著車聯網發展的日趨成熟,車聯網蠕蟲的傳播將受到人們的控制,該模型將不再適合車聯網蠕蟲傳播的后期,但是該模型的結論是車聯網蠕蟲傳播的極限情況。 隨著車聯網發展得不斷成熟,對于安全問題的解決將日趨完善,人們對于車聯網蠕蟲傳播的抑制也將越來越嚴格,因此不能不考慮尤其蠕蟲傳播后期人為干預對于車聯網蠕蟲傳播的影響。車聯網中蠕蟲可以感染的車輛可以劃分為感染類、易感類和恢復類。其中,易感類為車聯網蠕蟲可以感染的具有漏洞的車輛,感染類為被車聯網蠕蟲感染的車輛,恢復類為由于人為干預對于車聯網蠕蟲的查殺將感染類車輛轉化為恢復類車輛。車聯網中跟蠕蟲傳播相關的車輛只能處于感染類、易感類或者恢復類,易感類車輛可以被車聯網蠕蟲感染而轉化為感染類車輛,感染類車輛可以被人為查殺蠕蟲而轉化為恢復類車輛。下面根據漏洞車輛服從泊松或者高斯分布來分別討論車聯網蠕蟲的隨機傳播模型。 3.3.1 基于排隊論的車聯網蠕蟲的傳播模型 若如3.1節所述,車聯網蠕蟲在單位時間Δt內其感染車輛的數目服從泊松分布,即以均值λ感染車輛。若在單位時間Δt內,人們通過殺毒軟件或者其他方式查殺車聯網蠕蟲的數目為μ,因此其符合排隊論模型,那么其感染過程如下: 狀態查殺的速度=感染的速率 λP0=μP1,n=0 (λ+μ)Pn=λPn-1+μPn+1,n≥1 根據平衡方程的結果,得到等式: 或者等價地: 于是:而且,一般地: 因此有: 若使該隨機過程存在極限分布以及平穩分布的充分必要條件是上式中的分母有限,需要有: 因此,該模型存在極限分布以及平穩分布充要條件是λ<μ,即為了存在極限分布以及平穩分布,感染速率λ必須大于查殺速率μ;否則感染過程將不穩定或者導致傳播滅絕。 3.3.2 基于馬爾可夫鏈的車聯網蠕蟲的傳播模型 由于車聯網蠕蟲在單位時間tn+1時刻的傳播數目僅與tn時刻的傳播數目有關,因此其符合馬爾可夫鏈的傳播條件,傳播過程符合馬爾可夫鏈。那么其在較小的時間Δt內,車聯網蠕蟲從狀態n只能轉移到狀態n+1 或者n-1,或者保持不變。如3.1節所述,若車聯網蠕蟲感染主機的數目X~N(p×(r×300×i),(r×300×i)2σ2),那么其狀態轉移概率pjk為: 當j→j+1 時,其轉移率為b(k,j)=Φ((k-(p×r×100×i))/(σ×r×100×i))-Φ((j-(r×100×i×p))/(r×100×i×σ));當j→j-1 時,其轉移率為y(k,j)=rj;根據馬爾可夫鏈的性質,那么當j→j時,其轉移率為s(k,j)=1-rj-Φ((k-(r×100×i×p))/(r×100×i×σ))+Φ((j-(r×100×i×p))/(r×100×i×σ))。將其以矩陣的形式進行表示定義如下: 為了更加深入地驗證并且分析車聯網蠕蟲的傳播規律,編寫了可以模擬車聯網蠕蟲傳播的仿真器,仿真實驗對于相同的實驗內容進行1 000 次的重復操作,通過對于1 000次的實驗結果進行平均得到相應模型的傳播圖像。圖像的x軸表示感染主機數目,y軸表示單位時間,z軸表示感染的概率。下面對于實驗結果進行相應的討論。 圖2 是關于車聯網蠕蟲Galton-Watson 分支過程模型的仿真結果。其中,圖(a)為當車流服從泊松分布時,均值λ=0.8 時的仿真實驗結果。從圖中可以看到在蠕蟲傳播初期,蠕蟲可以進行小規模的傳播,但是隨著傳播的繼續,網絡蠕蟲則走向滅絕。這也驗證了定理2 的內容,即λ≤1 時,網絡蠕蟲必將滅絕。由于當車流服從正態分布且均值小于1 時實驗結果類似,這里就不再贅述。圖(b)為當車流服從泊松分布時,均值λ=2.0 時的仿真實驗結果,由于沒有網絡蠕蟲的查殺與防治,隨著蠕蟲感染時間的增加,網絡蠕蟲傳播規模不斷擴大的概率不斷加大,最終可以感染全部漏洞主機。圖(c)為當車流服從正態分布時,車流均值μ=5,σ2=25 時的仿真實驗結果。與車流服從泊松分布的結果類似,隨著蠕蟲感染時間的增加,網絡蠕蟲傳播規模不斷擴大的概率也是不斷加大,最終也可以感染全部漏洞主機。綜上所述,無論車流服從泊松還是正態分布,由于沒有人為干預車聯網蠕蟲的傳播,當其均值大于1 時,車聯網蠕蟲最終可以感染全部漏洞主機的概率較大。 圖3 是基于排隊論的車聯網蠕蟲傳播模型的仿真結果。其中,圖(a)為當λ=μ時的仿真實驗結果,從圖中可以看到在蠕蟲傳播初期,其僅可以進行小規模的傳播,但是隨著傳播的繼續,車聯網蠕蟲最終會走向滅絕。當λ<μ時,實驗結果結論相同,這里就不再贅述。這也驗證了3.3.1小節的結論,當λ≤μ時,車聯網蠕蟲將走向滅絕的結論。圖(b)、(c)、(d)為當λ分別為0.1、0.2和0.3,且μ為0.02時車聯網蠕蟲傳播模型的仿真結果。從圖中不難發現,在相同時間下,隨著λ的不斷增加,車聯網蠕蟲的傳播區間也在不斷擴大。例如,當單位時間為2 000 時,傳播區間從[130,180]擴大到[500,600]。也就是說,車聯網蠕蟲感染更多車輛的概率將會變得更大。 Fig.3 Simulation results of worm propagation model in Internet of vehicles based on queuing theory圖3 基于排隊論的車聯網蠕蟲傳播模型的仿真結果 Fig.4 Simulation results of worm propagation model in Internet of vehicles based on Markov chain圖4 基于馬爾可夫鏈的車聯網蠕蟲傳播模型的仿真結果 圖4 是基于馬爾可夫鏈的車聯網蠕蟲傳播模型的仿真結果。其中,圖(a)、(b)分別為當車流均值μ=10、20 且方差σ=10 不變時仿真實驗結果。從圖中不難發現隨著μ的不斷增加,車聯網蠕蟲的傳播區間也在不斷擴大。例如,當時間為2 000單位時間時,傳播區間從[28,38]擴大到[32,43]。圖(c)、(d)分別為當方差σ=10、15 且車流均值μ=20 不變時仿真實驗結果。從圖中不難發現,在相同時間下,隨著σ的不斷增加,車聯網蠕蟲的傳播區間跨度在不斷擴大。例如,當單位時間為2 000 時,傳播區間從[30,42]擴大到[30,50]。 本文提出了車聯網蠕蟲的隨機傳播模型。首先,在理想情況下,基于Galton-Watson分支過程對車聯網蠕蟲進行了建模;在現實情況下,當高速公路車流符合泊松分布時,基于排隊論對車聯網蠕蟲進行了建模,并且研究了穩定性條件。當高速公路車流符合正態分布時,基于馬爾可夫鏈對車聯網蠕蟲進行了建模。最后,通過仿真實驗驗證了提出的車聯網蠕蟲傳播模型。
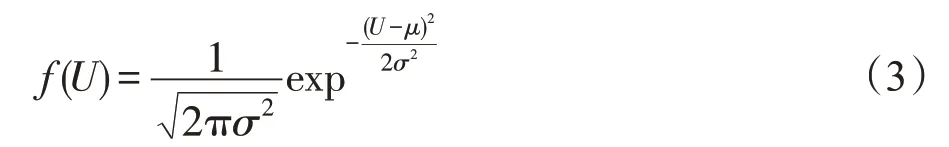


3.2 理想的車聯網蠕蟲隨機傳播模型


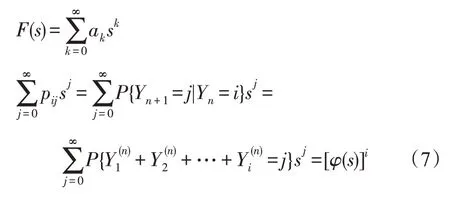

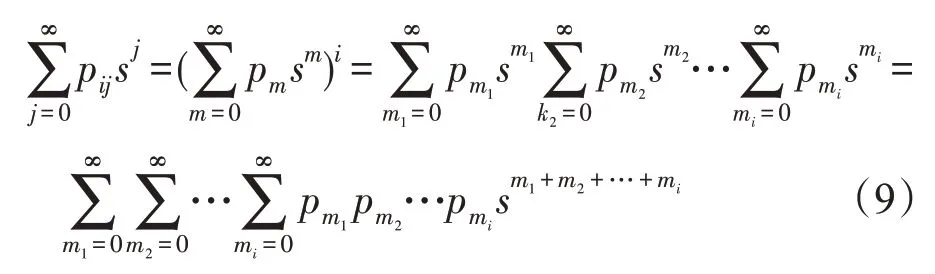




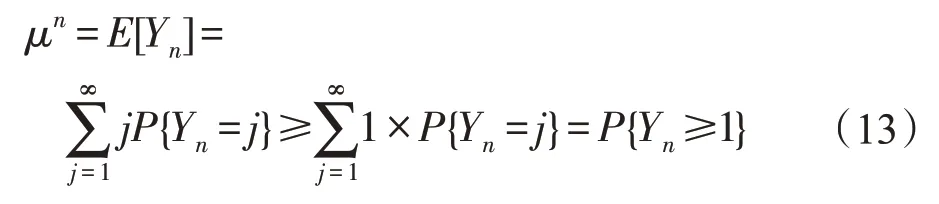
3.3 現實的車聯網蠕蟲隨機傳播模型


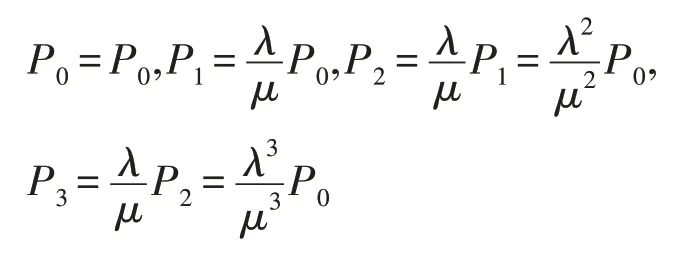




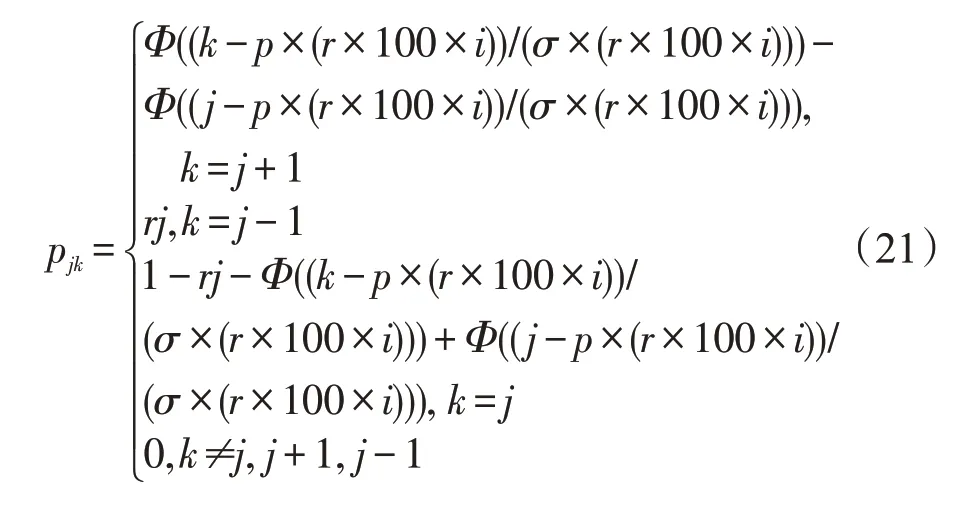

4 仿真驗證及分析
4.1 車聯網蠕蟲的Galton-Watson 分支過程模型
4.2 基于排隊論的車聯網蠕蟲的傳播模型
4.3 基于馬爾可夫鏈的車聯網蠕蟲的傳播模型
5 結論

