基于大數據的試井解釋參數分析

文必龍 李艷春

(東北石油大學計算機與信息技術學院 黑龍江 大慶 163318)

0 引 言

試井解釋是通過檢查、分析試井資料的特征獲取有關油藏信息和描述油藏物理本性參數的過程[1]。但是現階段的方法都是以圖版擬合為基礎，即實測曲線與理論典型曲線相比對得到最佳擬合理論曲線及擬合點，通過反演的方式反求地層參數[2-4]，對于圖版的選擇需要依靠解釋人員經驗指導，并且單井解釋需通過多組圖版進行比對。試井解釋智能化的概念在1986年石油國際會議上被格林加登提出，他認為試井解釋具有主觀推理特性，試井分析問題可歸納為人工智能問題，這推動了人工智能在試井領域中的應用研究[5]，成為現代試井解釋的標志。然而，傳統的人工智能算法所選用的數據量很小且趨于理想化，隨著試井數據采集量擴大，傳統的分析方法和人工智能算法的應用逐漸受到限制。因此，現有的試井解釋方法至少存在三方面不足：(1) 分析過程具有解釋人員主觀性使結果不唯一；(2) 圖版分析過程繁瑣且低效；(3) 專家的經驗不能復用。針對以上幾點不足，提出基于大數據的試井解釋方法，弱化圖版擬合的方式，利用多年試井解釋中長期積累的海量數據，通過數據驅動的方式結合大數據分析技術，挖掘試井解釋歷史數據與試井解釋結果間的潛在模式，構建試井解釋參數預測模型，從而利用壓力數據預測得到試井解釋結果。對海量歷史解釋數據進行有效的利用，減少人工參與和經驗對解釋結果的束縛，使復雜和專業性的試井解釋流程精簡化。

1 試井解釋大數據分析模式

多年試井解釋中積累了海量數據，這些數據的潛在價值是真實而巨大的[6]。在試井解釋大數據的支持下進行基于大數據的試井解釋參數分析，本質是對試井大數據隱含模式的探索并對未來情況的建模[7]，使試井解釋從經驗驅動轉變為數據驅動。本文參照跨行業數據挖掘標準流程CRISP-DM[8]設計了基于大數據的試井解釋參數分析流程，如圖1所示。

圖1 基于大數據的試井解釋參數分析流程圖

基于大數據的試井解釋參數分析流程主要分為以下步驟：

(1) 對試井解釋歷史數據中的壓力導數雙對數曲線進行分析，研究壓力導數雙對數曲線所反映的同類型試井的共性特征，以及曲線特征的描述方法。

(2) 對曲線特征與試井解釋參數進行相關性分析，確定模型構建所需的敏感性變量，與試井基礎數據構成試井解釋樣本庫。

(3) 通過分析試井解釋問題的求解類型，選擇合適的建模方法，構建試井解釋參數預測模型。

(4) 通過誤差分析結果，對模型進行調優，確定試井解釋參數的最終模型。以試井解釋壓力導數雙對數曲線數據作為輸入對試井解釋參數直接進行預測，替代使用圖版擬合并通過復雜方程求解的過程。

2 探索性數據分析

2.1 壓力導數曲線特征提取

試井解釋軟件通過計算機匹配擬合誤差最小的樣板曲線，但是由于只考慮數據總體誤差最小化，而沒有考慮曲線特征的作用，導致并不能匹配到解釋的最佳擬合位置。手動擬合分析用視覺估計實測曲線與樣板曲線的擬合誤差，往往同一組數據會存在多種解釋。而且曲線擬合所用的圖版是在某種參數組合的條件下繪制，即使同一類型的油藏實測曲線與理論曲線相比也存在平移、有噪聲等問題，二者不能完全統一。本文采用弱化圖版擬合的方式，通過實測曲線特征量化試井解釋經驗，采用特征組合的曲線描述方式，利用曲線特征數據直接進行解釋分析。

不同的試井壓力導數曲線的總特征不同，但是同一類型的試井壓力導數曲線的總特征存在共性，壓力導數曲線的早期、中期和晚期特征分別反映井筒、油藏及外邊界的情況[9]。傳統圖版擬合分析也是基于這一特性，最終都需要試井解釋專家根據曲線擬合效果更準確地找到樣本曲線與擬合位置，其依據是在雙對數曲線上，各種不同的油氣藏、不同的井類型、不同流動階段均有不同的特征[10]。描述曲線特征就是試井解釋的關鍵，利用特征組合方式進行曲線特征描述過程如下：

首先，根據試井曲線的特征進行特征點選擇，選定一組可以準確表述曲線峰值點和徑向流水平線的位置以及兩者之間關系的特征點。圖2為通過特征點描述曲線的顯著特征圖。

圖2 曲線特征點圖

其中：Start_point為壓力曲線與導數曲線重合起點；

Cross_point為壓力曲線與導數曲線重合的終點；

Top_point為壓力導數曲線的早期峰值點；

Radial_point1為壓力導數曲線徑向流段起點；

Radial_point2為壓力導數曲線徑向流段起點對應壓力值。

在雙對數坐標中通過Start_point、Cross_point和Top_point確定壓力導數曲線與壓差曲線的重合位置和壓力導數曲線早期峰值，通過Radial_point1和Radial_point2確定無限大徑向流階段0.5的水平線的位置。

其次，進行特征描述，細化特征點有效信息，確定雙對數曲線的形態和位置，如表1所示，通過特征點橫、縱坐標，時間比例，曲線構成面積等一系列屬性值來描述特征點與其臨近區域的相互關系。

表1 曲線特征屬性表

最后，以分析均質油藏的井筒儲集系數、流動系數和表皮系數三個試井解釋參數為例，利用曲線特征和解釋參數共同構成分析數據集。

2.2 數據預處理

基于大數據的試井解釋參數分析所需的信息全靠從數據中得來，但在壓力測試過程中會受到實際客觀條件和人為主觀條件的限制，導致測試數據出現不確定的測試偏差，這些偏差會直接影響試井解釋建模效果的好壞，因此在開始分析處理之前必須要對分析數據集進行修正。通過數據預處理改進數據的質量，使后面的分析結果和解釋模型更可靠。

對缺失數據的處理先探尋缺失值的來源，類似試井解釋基本數據井徑，油藏數據孔隙度、粘度這種特定不可替換的數據缺失，為不影響計算應采用剔除的方式；類似試井壓力數據這種連續型數據的缺失可以采用插值方式進行數據修正。

對于異常值的處理，其被視為異常的原因不同,在不明確數據集分布情況下可采用箱線圖來檢測異常值。箱線圖可清晰地顯示一組數據的分散情況，并提供識別異常值的一個標準：異常值被定義為小于Q1-1.5IQR或大于Q3+1.5IQR的值(Q1、Q3為上下四分位數，IQR為四分位距)[11]。圖3為利用箱線圖處理井筒儲集系數異常值的檢驗結果。圖3(a)中位于兩側虛線外側的均為異常值，對應的樣本數量稀少，應予以剔除，剔除后如圖3(b)，數據無異常值存在。

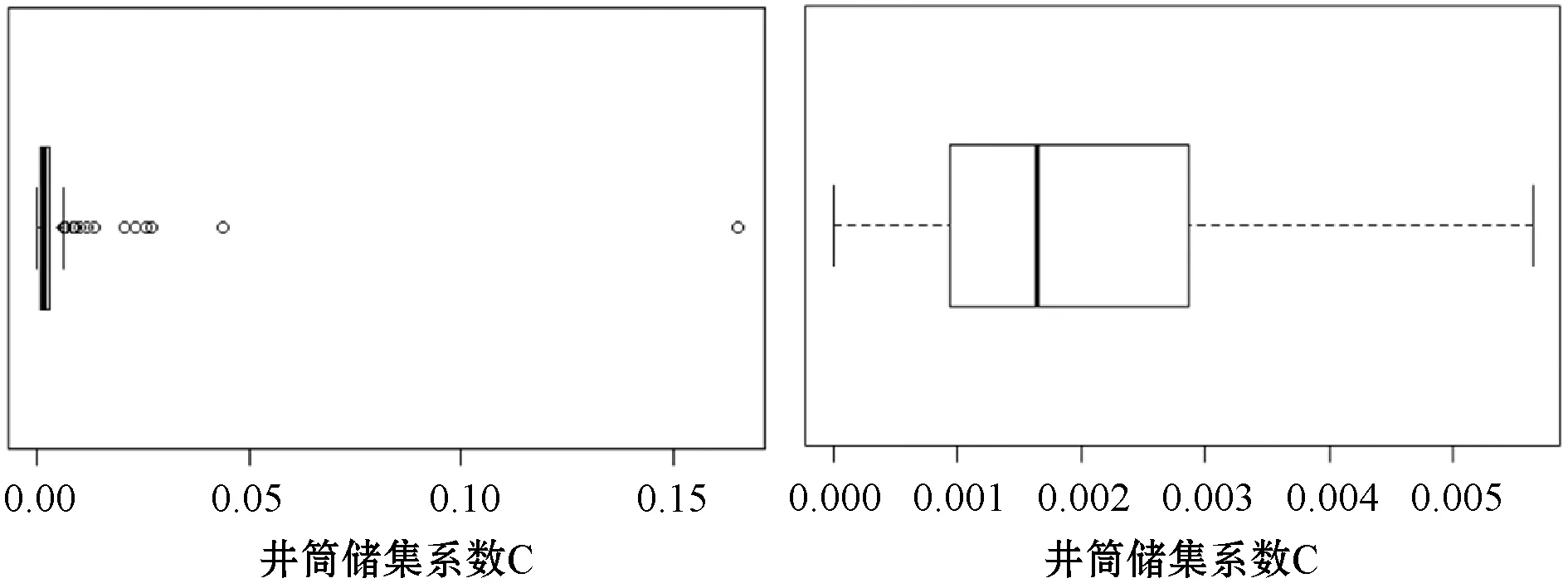
(a) 箱線圖-處理前 (b) 箱線圖-處理后圖3 井筒儲集系數異常值檢測

數據預處理后，對試井解釋結果原始數據進行K-S檢驗，驗證是否符合正態分布。如果檢驗P值大于0.05，則表明K-S檢驗的原假設成立，即原數據符合正態分布；若P值小于0.05，則不符合正態分布。以井筒儲集系數為例進行分布檢驗，其P值為0.131，可以認為服從正態分布。且預處理前井筒儲集系數的峰度和偏度分別為822.52和27.67，樣本進行預處理后其峰度和偏度分別為0.16和0.91，均小于1，說明樣本數據符合正態分布，如圖4所示為預處理前后分布情況對比。

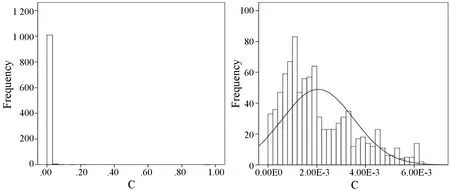
(a) (b)圖4 解釋參數分布情況對比圖

2.3 相關性分析

在基于大數據的試井解釋參數分析中更加關注數據總體，從數據的總體中可以直接獲取有價值的信息，大數據相關分析是大數據分析中對有價值信息挖掘的關鍵，曲線特征描述過多會導致信息冗余和模型的可解釋性降低，通過相關性分析能有效地發現與度量曲線特征與試井解釋結果之間的相關關系[12]。通過相關性分析來確定試井解釋參數預測中的敏感性變量，對整體的數據集合進行多變量的關聯性分析，從特征樣本庫的眾多輸入指標(不含解釋結果)，找出影響解釋結果參數(如流動系數、井筒存儲系數和表皮系數)的特征，將這些特征作為分析的實際特征，構建試井解釋樣本庫。

對預處理后得到的數據進行相關性分析，計算任意解釋參數與曲線特征之間的相關系數，度量此類數據相關性本節采用積距相關系數進行計算，計算公式如下：

(1)

式中：X和Y分別為解釋參數和曲線特征。

其樣本相關系數為：

(2)

由式(2)計算出解釋參數與曲線特征之間相關系數，通過表2所示的相關系數表衡量兩者之間的相關關系，相關系數越大則認為曲線特征對解釋參數的影響越大，將表中相關系數較大的特征選進試井解釋樣本庫中，用于最終預測模型的建立。

表2 解釋參數相關系數表

為更直觀地表述兩者的相關關系，繪制如圖5所示的相關性矩陣，當曲線特征與解釋參數相關性矩陣中被觀察變量之間存在相關關系時，數據點會呈現一個集中趨勢[13]。

圖5 曲線特征與解釋參數相關性矩陣圖

通過表2相關系數和圖5相關性矩陣分析比較變量之間的相關性，可以發現井筒儲集系數受Strat_Cor和Cross_Cor的動態影響；流動系數受Top_Hor、Top_Cor、Radial_Cor和Cross_Cor的動態影響；表皮系數受Radial_Differ和Cross_Differ的動態影響。這說明井筒儲集系數與壓力導數雙對數曲線的早期形態有關，流動系數與壓力導數曲線駝峰出現的時間以及峰值點的位置有關，表皮系數與兩條曲線開口大小(即縱坐標差值)有關，以此篩選出特征數據集作為模型的輸入集符合正態分布。

3 試井解釋大數據分析模型

3.1 模型構建

不同類型的試井存在總體特征相同，具體存在差異的問題，所以試井解釋參數的預測方法需要有很強的適應性，而神經網絡具有函數逼近能力，能自動逼近學習范圍內的任意插值情況[14]，故使用神經網絡方法來建立基于大數據的試井解釋參數預測模型。通過相關性分析對曲線特征數據進行有效降維，保留與各解釋參數有很大關聯度的敏感性變量，作為神經網絡模型構建的輸入變量，從而構建試井解釋參數預測模型。

模型的具體設定如下：

(1) 輸入層：輸入層節點對應于模型的輸入變量，本模型中輸入節點由曲線特征變量決定。

(2) 輸出層：輸出層節點對應預測目標，本模型中輸出節點由試井解釋參數決定，本文中只討論井筒儲集系數、流動系數和表皮系數三個試井解釋參數，故輸出層節點數為3。

(3) 隱含層：隱含層的神經元數太少，網絡不能很好地學習，需要訓練的次數較多，精度也不高;神經元數太多，則導致訓練時間較長，甚至不收斂。經過多次調試實驗，隱含層數目為10時，神經網絡對函數的逼近效果最好。

(4) 樣本選擇：預測模型的樣本數據為某地區均質油藏的Gringarten-Bourdet圖版的歷史試井解釋數據，盡管學習樣本不可能覆蓋所有可能的參數值，但神經網絡具有自適應性，實測曲線特征和解釋參數的度量在學習范圍內，不管學習樣本是否與之完全吻合，模型都能給出預測值[15]。

(5) 模型驗證：采用保持樣本的方法對預測模型進行驗證，把學習樣本劃分為訓練集和檢驗集，以訓練集進行模型訓練，以檢驗集進行正確率評估。

3.2 模型優化

為提高模型預測精度，對特征數據集進一步采取雙變量分析。以分析Kh/μ(流動系數)與Radial_Cor為例進行雙變量分析，如圖6(a)所示，Kh/μ與Radial_Cor存在相關性，但兩者之間的相關關系呈現出多條趨勢線。進一步探究分析發現呈現多條趨勢線是由于數據來源于不同井造成的，試井解釋參數模型是通過數據的共性特征構建通用模型，可通過特征工程對模型的輸入輸出進行變量轉換。通過下式可以發現擬合值pm是與單井信息無關的變量，采用預測pm代替Kh/μ消除數據來源于不同井對預測的影響，提高模型的預測精度。

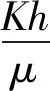
(3)

圖6(a)和圖6(b)分別是Kh/μ和pm與Radial_Cor相關性分析圖，顯然進行特征變換后變量間相關性明顯增強。對其他兩個參數也采用相同的方法進行處理，由于弱化圖版的概念對時間擬合值、壓力擬合值以及曲線參數cDe2s只作為一個擬合值的數據集，分別表示為tm、pm和cm。通過預測擬合值間接預測解釋參數，分析數據源由曲線特征數據集與試井解釋結果變為曲線特征數據集與擬合值數據集，進而通過擬合值的預測結果求得試井解釋參數。

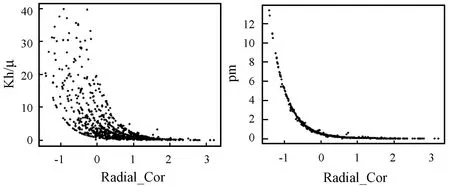
(a) (b)圖6 曲線特征與解釋參數雙變量分析圖

對于不能直接通過變量替換解決的問題，可以通過特征工程進行新變量和新特征的創造，井筒儲集系數C與tm、pm兩個擬合值都存在聯系，需通過tm、pm兩個擬合值提取一個間接擬合值pm/tm，記為pm_tm來替代C，并構建新特征值Radial_Top(通過Top_Hor與Radial_Cor擬合得到)。C的表達式如下：

(4)

對特征數據集與擬合值數據集的分析得到表3相關系數表，重新構建模型的網絡結構，并對模型進行訓練，從而得到最終的試井解釋參數預測模型。

表3 擬合值相關系數表

3.3 模型評估

采用前文提到的保持樣本的方法模型進行驗證，通過訓練后的試井解釋參數預測模型對測試樣本進行預測，如圖7(a)所示，星號為表皮系數預測輸出值(預測值)，圓圈為表皮系數期望輸出值(實際值)，預測值在實際值上下浮動，基本與實際值重合。由圖7(b)可知，測試樣本預測誤差均分布在[-1，1]之間，大部分集中于[-0.5，0.5]，偏離零點線程度不大，故該模型的預測誤差在一個可以接受的范圍內，說明模型預測效果比較好。

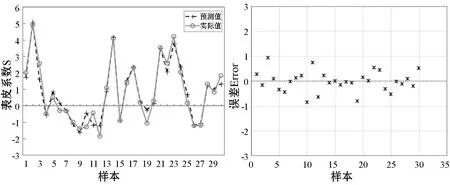
(a) (b)圖7 模型表皮系數(S)預測值與期望值誤差和對比

由圖8可以看出，訓練樣本和測試樣本中表皮系數預測值和實際值的數據點擬合效果較好，集中于擬合線y=x附近，說明模型訓練和測試性能較好且穩定。由表4可知模型其他試井解釋參數的預測情況，表皮系數的訓練樣本預測值和實際值相關系數為0.978 9，測試樣本預測值和實際值的相關系數為0.975 3；井筒儲集系數的訓練樣本預測值和實際值相關系數為0.977 3，測試樣本預測值和實際值的相關系數為0.976 8；流動系數的訓練樣本預測值和實際值相關系數為0.983 4，測試樣本預測值和實際值的相關系數為0.990 4，相關系數均處于穩定，說明模型泛化能力較佳。

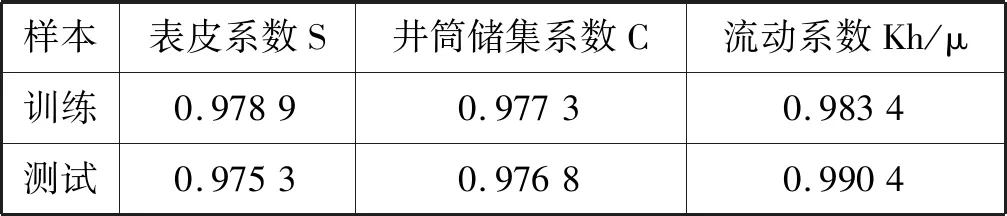
表4 模型訓練和測試的預測值和實際值的相關系數

4 實例分析

利用本文所訓練的模型對歷史試井數據進行分析,并與傳統試井解釋方法進行對比。

4.1 基礎數據

生產時間為91.75 h，常產量為2.17 m3/d，原油體積系數為1.198，綜合壓縮系數為0.145 9×10-4MPa-1，油層厚度為3 m，測試井半徑為0.069 85 m，原油黏度為0.8 mPa·s，孔隙度為0.222。實測記錄的壓力及壓力導數雙對數曲線見圖9。

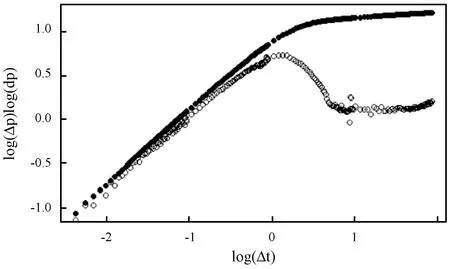
圖9 實測記錄的壓力及壓力導數雙對數曲線圖

4.2 結果比對

原解釋結果：流動系數為0.711 0-3μm2.m/mPa.s；井筒存儲為0.002 5 m3/Mpa；表皮系數為2.01；神經網絡模型計算解釋結果：流動系數為0.701 0-3μm2.m/mPa.s；井筒存儲為0.002 7m3/Mpa;表皮系數為1.73。預測結果與原解釋結果相吻合，證明了基于大數據的試井解釋參數分析方法的可靠性，且解釋流程更加精簡化，避免了圖版擬合的固有誤差和解釋人員主觀性對解釋結果的影響。

5 結 語

本文提出的方法運用大數據分析，以試井解釋分析的歷史數據為依據，深挖壓力導數雙對數曲線與試井解釋參數的關聯關系，提出曲線特征的描述方法量化同類型試井的共性特征，采用相關分析確定與試井解釋參數相關的獨立變量，進而通過神經網絡輔助進行模型構建。利用神經網絡的函數逼近能力，克服了傳統圖版只能包含部分典型曲線的局限性，消除了傳統圖版分析的固有誤差，以弱化圖版擬合的方式減少人工參與對擬合結果的束縛，使試井解釋過程更簡捷。利用此方法，解決單井解釋需要多組典型曲線圖版的不足，消除傳統方法的復雜性及多解性，一次解釋確定所有參數。

本文研究的雖然是用于均質無限大油藏圖版擬合分析的Gringarten-Bourdet圖版的解釋結果，但方法可以很容易地進行推廣，其意義不僅在于實現這一類問題的分析智能化，更在于為試井解釋提供了智能分析新方法，結束需要多組圖版聯合分析的歷史。