復合油藏壓裂水平井復雜裂縫分布壓力動態特征

徐有杰，劉啟國，王 瑞，劉義成

（1.西南石油大學石油與天然氣工程學院，成都610500；2.石油工業出版社，北京100000；3.中國石油西南油氣田分公司勘探開發研究院，成都610000）

0 引言

我國非常規油氣資源豐富、發展潛力大，高效開發非常規油氣資源對于滿足我國能源需求具有重要意義［1-2］。隨著水力壓裂技術的不斷進步，為了改善油藏的開發效果，通常對水平井實施多段射孔壓裂，增加油藏泄油面積，改善儲層與井筒之間的流體連通狀況，從而提高單井產量［3-4］。壓力動態特征分析作為油氣藏評價以及儲層物性參數求取的重要手段，對于指導油氣田開發具有重要意義。

點源函數的發展對于求解儲層滲流模型解析解起到了重要作用。在早期，Gringarten等［5］基于Green函數得到實空間源函數解；Ozkan等［6-7］成功地將實空間源函數解擴展到Laplace空間；Cinco-Ley等［8］建立并求解了傾斜水力壓裂裂縫試井解釋數學模型。水力壓裂裂縫的分布因水力壓裂過程中各種地質因素的存在而變得十分復雜［9］。關于水力壓裂所形成的復雜裂縫試井模型，國內外均有研究，分別針對不對稱縫［10-11］、多翼裂縫井［12］試井模型開展了研究，分析了其主控因素對壓力和產量曲線的影響。多段壓裂水平井對于高效開發儲層原油具有重要的作用，研究其壓力動態變化特征成為油氣開發的重要環節，一些學者［13-21］對多段壓裂水平井壓力和產量模型進行了研究，考慮了裂縫傾斜和裂縫不對稱的影響。水力壓裂過程中井筒附近往往會形成壓裂改造區，該區域儲層滲透率高于儲層原始滲透率。何吉祥等［22］和袁淋等［23］針對氣、水兩相壓裂水平井產能計算給出了相關公式，并分析了水氣體積比對產量曲線的影響。關于多段壓裂水平井體積壓裂改造試井模型的研究，姜瑞忠等［24］、蘇玉亮等［25］、李道倫等［26］分別針對復合油藏多段壓裂水平井試井模型展開研究，繪制了相應的典型特征曲線，并進行了影響因素分析。

在實際多段壓裂體積改造時，由于地層條件復雜，導致井筒附近形成了復雜的縫網體積，因此，在前人研究成果的基礎上，對水平井體積壓裂改造試井模型進一步研究十分必要。針對水力壓裂所形成的復雜裂縫，首先分別建立儲層和裂縫試井解釋數學模型，通過Laplace積分變換求得Laplace空間解析解，其次耦合儲層與裂縫模型求解得到其均勻流量面源解，采用裂縫離散的方式求得Laplace空間井底壓力解，最后通過Stehfest數值反演計算并繪制雙對數曲線圖，分析裂縫分布方式以及改造區半徑對典型特征曲線的影響，以期為多段壓裂水平井試井資料解釋和壓裂方式設計提供理論依據。

1 物理模型描述

在水力壓裂過程中由于地層條件等各種因素的影響，使得實際多段壓裂水平井水力壓裂裂縫分布不規律。水平井經多段壓裂之后井筒附近儲層的滲透率高于距井筒較遠區域，即井筒附近由于壓裂體積改造形成了壓力改造區（內區），而未改造區（外區）儲層滲透率不變。為了更好地建立水平井體積壓裂改造試井數學模型，可以將多段壓裂水平井裂縫分布物理模型抽象為徑向復合模型，內區半徑為rm（圖1）。其他假設條件如下：①內區和外區儲層平均滲透率分別為k1，k2；②水平井位于頂底封閉、側向無窮大外邊界儲層中；③裂縫寬度為wf且相等，第i條裂縫長度為Lfi，與井筒的夾角為θi，裂縫內滲透率為kf；④流體在儲層和裂縫中的流動符合達西滲流規律，且為等溫滲流；⑤每條裂縫都完全壓開，即裂縫高度與儲層厚度相等。

圖1 多段壓裂水平井裂縫分布物理模型示意圖Fig.1 Schematic diagram of fracture distribution of multi-stage fractured well

2 數學模型的建立與求解

根據上述假設條件，頂底封閉、側向無窮大外邊界存在點源P，t=0時刻從點源中采出流體的流量為～q，而該時刻采出流體的流量使得線源周圍的壓力波向外傳播，進而使得內外區的流體均流入井筒（圖2）。

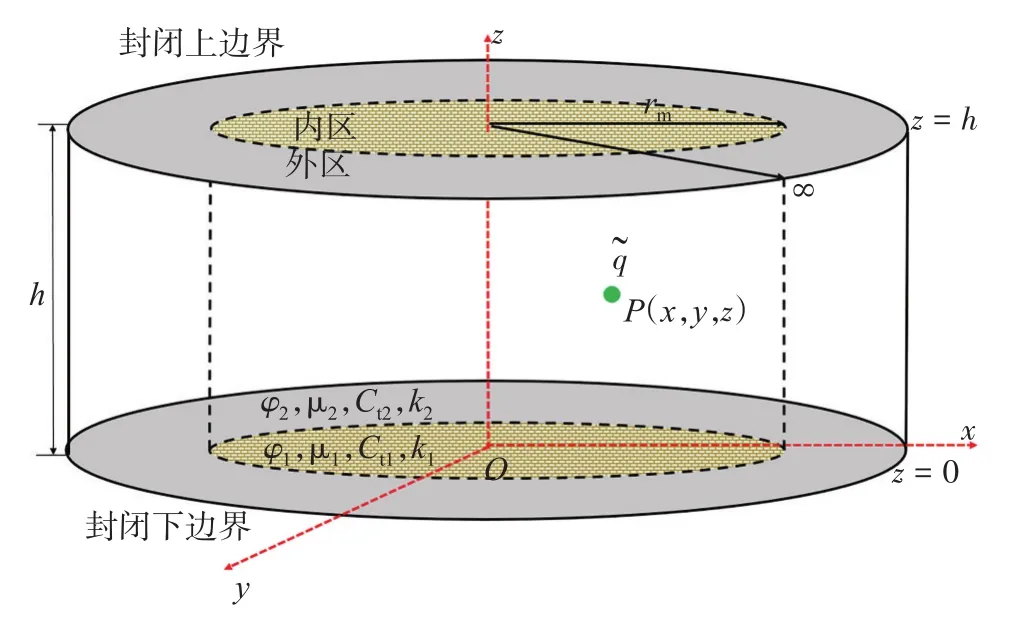
圖2 徑向復合油藏點源物理模型示意圖Fig.2 Point-source schematic diagram with radial composite reservoirs

2.1 儲層數學模型的建立與求解

對于多段壓裂水平井復雜裂縫井底壓力的計算，先以裂縫的單翼為研究對象建立儲層試井解釋數學模型，再根據壓降疊加原理得到M條裂縫總的井底壓降。根據狀態方程、運動方程和連續性微分方程，分別得到無因次內區與外區滲流數學模型和邊界條件，無因次變量定義為其中：C為井筒儲集系數，m3/MPa；CfD為無因次裂縫導流能力；Ct為綜合壓縮系數，MPa-1；h 為儲層厚度，m；k1，k2分別為內、外區儲層平均滲透率，D；kf為裂縫滲透率，D；Lf為裂縫長度，m；Lref為參考長度，m；M12為內外區流度比；p1，p2分別為內、外區儲層壓力，MPa；pf為裂縫壓力，MPa；pw為考慮井儲和表皮效應的井底壓力，MPa；pe為原始儲層壓力，MPa；pwH為不考慮井儲和表皮效應的井底壓力，MPa；qsc為地下生產總流量，m3/d；r為任意位置徑向距離，m；rm為內區半徑，m；t為生產時間，h；Wf為裂縫寬度，m；x，y，z為計算點位置，m；xw，yw，zw為點源所在位置，m；ε為無窮小長度，m；～qf為裂縫線流量，m2/d為瞬時線源流量，m2/d；φ1，φ2分別為內、外區介質孔隙度，%；μ1，μ2分別為內、外區流體黏度，mPa·s；η12為導壓系數比；下標D表示無因次。

關于無因次時間進行Laplace變化，得到Laplace空間方程組為

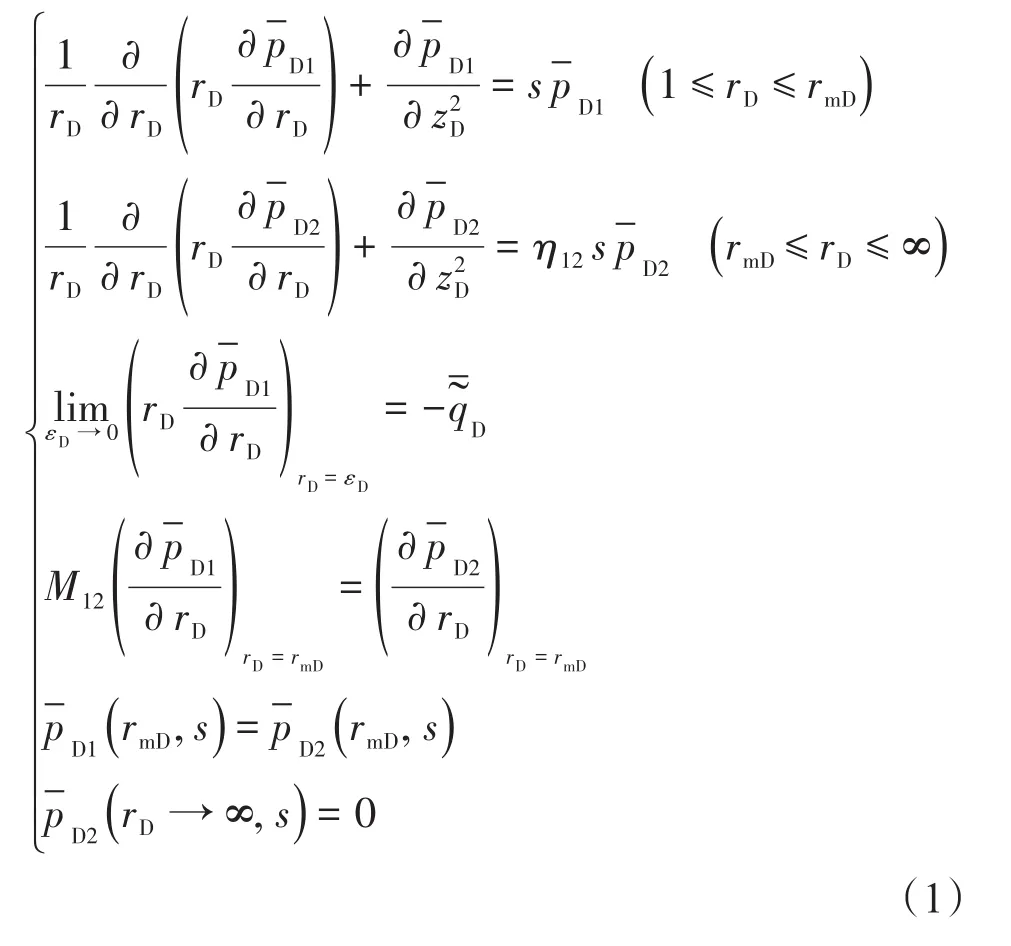
分別對內區和外區滲流微分方程關于zD從0到hD進行有限余弦Fourier變換，得到只考慮徑向方向的徑向復合滲流微分方程，根據Bessel方程基本解的結構，得到內外區滲流微分方程的通解，再根據有限余弦Fourier逆變換得到內外區任意位置處點源解為

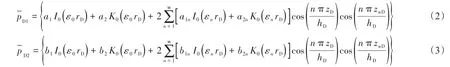
其中

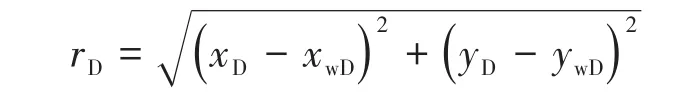
式中：s為拉普拉斯變量；I0（x）為零階第1類修正Bessel函數；K0（x）為零階第2類修正Bessel函數。

聯立內外邊界條件并根據內外區界面條件得到式（2）和式（3）中的系數分別為

根據 Ozkan 等［6-7］和 Restrepo 等［27］的研究，為了求得任意形狀裂縫的井底壓力解，對式（2）分別關于zD從0到hD和關于xD從0到LfD積分得到均勻流量面源解，再根據坐標變換和坐標旋轉得到第i條裂縫均勻流量面源解為

根據質量守恒關系，M條裂縫的總流量等于每條裂縫流量的總和。

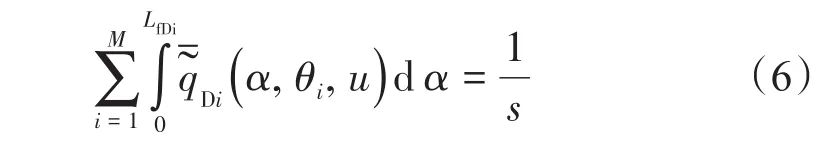
2.2 裂縫數學模型的建立與求解

基于 Cinco-Ley等［8］的研究，建立裂縫數學模型，經坐標旋轉之后使裂縫沿坐標方向分布，假定所有裂縫的寬度都相等，基于滲流力學基本原理，第i條裂縫Laplace空間無因次裂縫數學模型為

2.3 儲層與裂縫模型耦合求解

在裂縫壁面處壓力和流量相等，根據裂縫模型與儲層模型在裂縫壁面處的銜接條件得到井底壓力解。因此，有如下表達式：

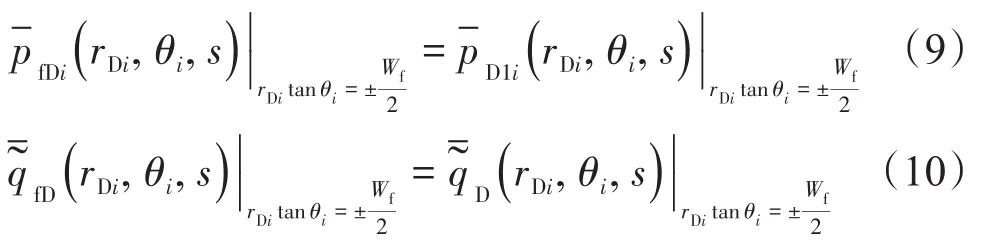
將式（4）、式（9）和式（10）代入式（8）得到

式（11）中含有Fredholm積分方程，直接求解比較困難，基于均勻流量模型解，將每條裂縫離散為N 段，每段流量均不變，式（6）和式（11）離散之后的表達式為

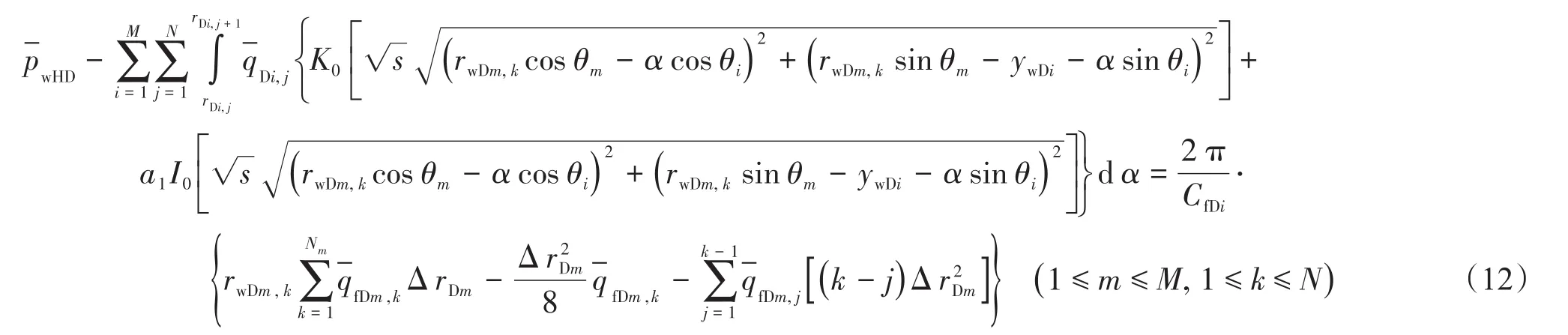
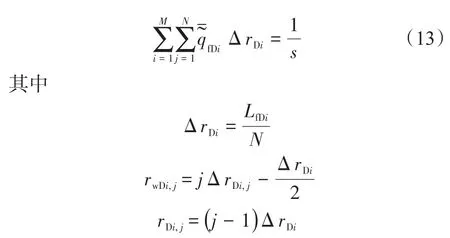
式中：Δ rDi為第i條裂縫第j個網格步長；rwDi,j為第i條裂縫第j個網格中點；rDi,j為第i條裂縫第j個網格端點；M為裂縫條數；N為裂縫離散個數。

利用上述M×N+1個方程組求得M×N+1個未知數，從而求得井底壓力解。

當裂縫條數M=2時，裂縫不對稱因子定義為

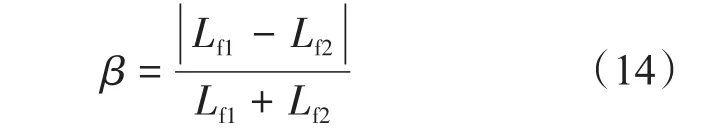
根據Duhamel原理，考慮井儲和表皮效應影響時無因次井底壓力表示為

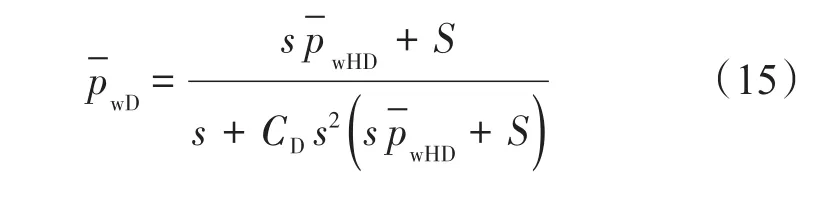
3 模型驗證與特征曲線分析

3.1 模型驗證

在進行模型驗證時，如果本文模型M=2，Lf1=20，Lf2=60，θ1=0°，θ2=180°，該模型就可以簡化為不對稱垂直裂縫，并與文獻［11］針對不對稱垂直裂縫的計算結果進行對比。對于有限導流裂縫而言，裂縫導流能力的大小對于計算的準確性和精度都有很大的影響，因此，分別取無因次裂縫導流能力為1和10進行對比，從圖3可以看出無論無因次裂縫導流能力是大還是小，文獻［11］的計算結果都能與本文簡化模型計算結果吻合。需要注意的是，當裂縫導流能力很低時，將單個裂縫離散的段數越多，計算結果越準確。

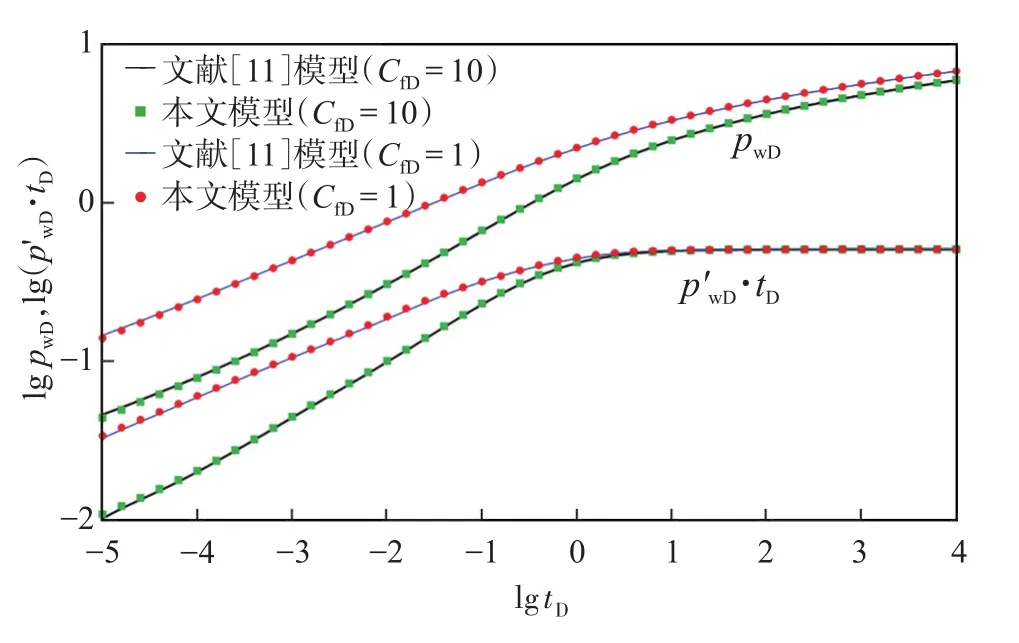
圖3 模型驗證對比Fig.3 Comparison of model verification

3.2 特征曲線分析

圖4為復合油藏多段壓裂水平井復雜裂縫分布井底壓力響應特征曲線。根據壓力導數曲線特征，該典型特征曲線可以分為9個流動階段：第Ⅰ階段為井儲階段，純井儲階段該曲線特征表現為壓力和壓力導數曲線重合，且斜率均為1；第Ⅱ階段為雙線性流階段，該階段儲層內流體向裂縫流動和裂縫內流體向井筒流動同時發生，理想狀態下該階段壓力導數曲線呈斜率為1/4的直線；第Ⅲ階段為線性流階段，該階段只有儲層內流體向裂縫流動，理想狀態下該階段壓力導數曲線呈斜率為1/2的直線；第Ⅳ階段為早期橢圓流階段，該階段為流體圍繞單個裂縫的橢圓流；第Ⅴ階段為早期徑向流階段，該階段為流體圍繞單個裂縫的徑向流，壓力導數曲線為0.5/M的水平線；第Ⅵ階段為過渡流階段；第Ⅶ階段為內區徑向流階段，該階段為內區流體圍繞水平井的徑向流，壓力導數曲線為0.5的水平線；第Ⅷ階段為內區向外區過渡流階段；第Ⅸ階段為外區徑向流階段，該階段為整個儲層流體圍繞水平井的徑向流，表現為外區徑向流特征，壓力導數曲線為0.5 M12的水平線。

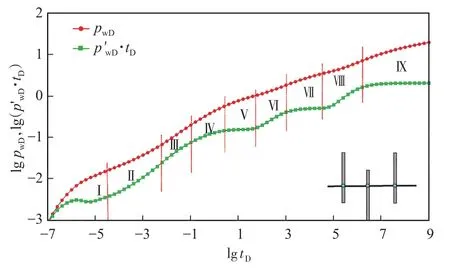
圖4 復合油藏多段壓裂水平井復雜裂縫分布井底壓力響應特征曲線Fig.4 Wellbore pressure response curve of multi-stage fractured horizontal well with complex fracture in composite reservoirs

3.3 裂縫分布對曲線的影響

圖5為裂縫分布方式對壓力響應特征曲線的影響。地層應力分布不均勻和射孔壓裂都會導致壓裂裂縫呈現出不對稱分布、單側交錯分布、不對稱交錯分布及呈一定夾角分布。單裂縫呈現出不對稱分布時，裂縫不對稱只影響早期線性流和雙線性流階段壓力和壓力導數曲線的變化，裂縫越不對稱，早期階段流體流入井筒所消耗的壓力越大，壓力和壓力導數曲線均越高［圖5（a）］。在水平井長度和裂縫條數相等的條件下，當沿水平井一側壓開或以一定的夾角兩側壓開時，裂縫與井筒夾角越小，流體流入裂縫所消耗的壓降越大。當裂縫單側壓開時，由于b情形縫間距離是c情形的一半，因此，早期徑向流階段壓力導數曲線低［圖5（b）］。當裂縫呈a，b，c等3種情形分布時，c情形下流體流入井筒所消耗的壓力最低。當裂縫與井筒存在一定夾角時，裂縫與水平井筒所存在的夾角越小，裂縫所控制的流體范圍越小，裂縫與裂縫之間的干擾性越強，因此，裂縫與井筒之間的夾角越小，雙對數坐標壓力和壓力導數曲線均越高［圖5（c）］。裂縫交錯分布可以有效地擴大裂縫控制區域，當裂縫呈現不對稱式交錯分布時，裂縫與裂縫之間長短互補可以有效地使井筒附近流體流入井筒時所消耗的壓力變小，因此，相比于對稱分布和不對稱分布，當裂縫呈不對稱交錯分布時早期壓力和壓力導數曲線均最低［圖5（d）］。

圖5 裂縫分布方式對壓力響應特征曲線的影響Fig.5 Effects of fracture distribution on wellbore pressure response curves

結合以上幾種裂縫分布方式來看，當裂縫呈不對稱交錯分布時可以更有效地降低流體流入井筒所消耗的壓力，從而可以最大限度地提高單井產量。因此，在實際壓裂過程中應避免裂縫不對稱分布、單側分布及呈夾角分布的情形。

3.4 內區半徑大小和流度比對曲線的影響

圖6反映了內區半徑大小和流度比對壓力響應特征曲線的影響。水平井體積壓裂之后所形成的內區大小和內區滲透率大小都對壓力響應特征曲線有很大的影響。內區半徑主要影響內區徑向流持續時間長短和曲線形態，較大的內區半徑容易形成內區徑向流，因此，在壓力導數曲線上其0.5水平線也越長；此外，內區半徑越大，儲層改造范圍越大，流體流入井筒所消耗的壓力損失越小，對應的壓力曲線越靠下［圖6（a）］。內外區流度比是指徑向復合油藏內區與外區流動系數比值的大小，內外區流度比越大，外區徑向流階段壓力導數值為0.5 M12的水平線越高。由于內區滲透率增大，流體流動阻力減小，因此，內外區流度比越大，對應的壓力曲線越高［圖6（b）］。

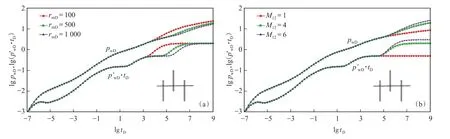
圖6 內區半徑（a）和內外區流度比（b）對壓力響應特征曲線的影響Fig.6 Effects of inner radius（a）and mobility ratio（b）on wellbore pressure response curves

4 結論

（1）綜合考慮裂縫不對稱、裂縫夾角等因素，建立了徑向復合油藏多段壓裂水平井復雜裂縫分布試井數學模型，通過Laplace變換和Stehfest數值反演得到了定產條件下的井底壓力解。通過對比、分析，驗證了本文模型的正確性。

（2）根據壓力導數曲線特征，本文模型壓力動態特征曲線主要的流動階段有6個，即井儲階段（斜率為1）、雙線性流階段（斜率為1/4）、線性流階段（斜率為1/2）、早期徑向流階段（0.5/M水平線）、內區徑向流階段（0.5水平線）和外區徑向流階段（0.5 M12水平線）。

（3）綜合分析各種裂縫分布方式，當裂縫不對稱交錯分布時壓裂改造效果最好，壓力曲線越低；內區半徑越大，內外區流度比越小，外區徑向流階段壓力曲線越靠下。