基于線性穩定性分析的翼尖渦搖擺機制

邱思逸，程澤鵬，向陽，劉洪

上海交通大學 航空航天學院，上海 200240

翼尖渦是飛機尾跡中一種典型的大尺度渦結構，大型客機的翼尖渦可以在100倍機翼弦長的尾跡區域內維持，從而對后續飛機的安全飛行產生威脅，限制了機場起降頻率[1]。此外，由翼尖渦誘導下洗產生的誘導阻力是飛機阻力的主要來源之一[2]。Gerz等在2002年總結提出了控制飛機尾跡渦影響的兩大策略：① 減弱翼尖渦強度；② 使翼尖渦快速衰減[1]。目前通過加裝翼梢小翼等流動控制方法可以有效地減少翼尖渦強度，然而針對第2種策略卻缺乏有效的流動控制原理及方法。事實上，已有研究表明，渦的破碎和耗散與其不穩定性特征密切相關[3]，而翼尖渦在演化過程中包含明顯的不穩定性特征，其在一定條件下表現為低頻的搖擺運動(Vortex Wandering)[4-5]，這種現象目前被認為主要由翼尖渦內在的不穩定性導致[6]，且在整個尾跡區內其不穩定性存在主導頻率[7-9]。通過施加與此頻率相匹配的流動控制，或者利用渦系間的相互作用，增大翼尖渦不穩定性的放大率[1，10]，使流動提前進入由短波或長波不穩定性[11]主導的快速耗散狀態，可以實現翼尖渦的快速衰減；此外，已有研究者利用流動不穩定性的響應頻率實現了有效的非定常推進[12]，表明不穩定性是一種值得深入研究并加以利用的流動內在特性。因此，研究翼尖渦搖擺運動，可以明確不穩定性特征對翼尖渦流動的影響機制；在此基礎上，有助于進一步利用流動不穩定性的頻率或模態特征激發翼尖渦發生失穩，通過非定常的流動控制策略對翼尖渦實施控制。

搖擺運動是翼尖渦在其不穩定性特征作用下所呈現的具體現象之一，表現為翼尖渦在流向截面內擬序的低頻振蕩，最初由Baker等在水槽試驗中發現[4]。由于搖擺運動使翼尖渦物理參數的測量與求解產生誤差，消除搖擺運動對實際流場測量的影響以及探尋其內在的物理機制一直是研究者的重點關注所在。Devenport等首次對翼尖渦搖擺現象予以修正，通過聯合概率密度函數近似表征瞬時渦核位置分布，并使用反卷積修正法消除翼尖渦搖擺對測量的影響，在此基礎上得到了清晰的遠場翼尖渦湍流相干結構[5]；同時在較小斯特勞哈爾數的條件下，觀察到了翼尖渦搖擺的各向異性現象。對于粒子圖像測速(PIV)試驗測量得到的翼尖渦流場，可以使用渦核重新定位的方法進行修正[6,13]。Deem等比較了上述兩種方法對翼尖渦搖擺的修正效果，結果表明瞬時渦核位置分布滿足高斯分布，且搖擺運動表現出各向異性的特點[14]。試驗研究發現，翼尖渦搖擺幅值隨流向增長[13]，且隨迎角[15-16]與渦強度[13]的增大而減小。薛棟使用單點譜分析和動力學模態分解技術得到在雷諾數103量級下，翼尖渦搖擺的主頻率約為1 Hz[8]，也表明了搖擺運動存在主導頻率。在此基礎上，Edstrand等比較了理論Q渦模型的線性穩定性分析結果和翼尖渦試驗數據的本征正交分解模態，證明了翼尖渦搖擺來源于其內在不穩定性特征[6]。由此可見，對于翼尖渦搖擺現象已經有相對成熟的修正方法，但是在穩定性作為翼尖渦搖擺主要原因的基礎上，翼尖渦搖擺現象自身的演化規律和機理仍沒有明確的闡釋，穩定性對翼尖渦流動具體的影響機制也需要進一步分析。

通過線性穩定性分析(Linear Stability Analysis,LSA)可以計算得到翼尖渦流動的不穩定性放大率、擾動頻率和擾動模態，從而對翼尖渦的不穩定性特征進行定量的分析研究[17-20]。最初，一些研究者使用線性穩定性分析對不同翼尖渦理論模型的穩定性進行了參數化的研究。Mayer和Fabre等使用線性穩定性分析對翼尖渦的理論Batchelor渦模型[21]的研究結果表明，翼尖渦的不穩定性受其旋擰度(Swirl Parameter)、擾動周向波數n、雷諾數Re和黏性影響，增大旋擰度對翼尖渦具有穩定作用，而增大雷諾數會減弱旋擰度的穩定效果[22-23]。同時，研究發現擾動周向波數n=-1的螺旋模態是最不穩定的[22-24]，不穩定性隨周向波數n增加而遞減；并且有黏流動相比無黏流動更穩定[24]。然而以上研究都是基于翼尖渦理論模型，較難反映實際流動的穩定性。因此，有研究者對試驗數據擬合的流動解析解或直接數值模擬(DNS)結果進行線性穩定性分析，從而得到更接近真實的流動穩定性特征。Oberleithner等對試驗測得的旋轉射流的線性穩定性分析結果表明，這種流動存在一種自激勵的全局模態，且該模態存在主導頻率，并通過LSA和POD分析分別重構了這種流動的三維擾動速度場[7]；Edstrand等使用Bi-Global LSA分析了DNS(Re=1 000)得到的近場尾跡區的翼尖渦流動，探討了后緣尾跡對翼尖渦穩定性的影響[25]。然而，目前對于翼尖渦不穩定性放大率、擾動頻率等不穩定性參數隨流向的變化過程缺乏明確的定量化研究，在一定程度上限制了對于不穩定性對翼尖渦搖擺運動作用機制更深入的理解。

綜上所述，對于翼尖渦搖擺現象的研究主要集中于對其進行修正以獲取更準確的翼尖渦流場；雖然穩定性作為翼尖渦搖擺的內在原因已得到初步證實，但是翼尖渦搖擺現象自身的演化規律和機理尚需更深入的研究，其演化特性與不穩定性的關系也仍需進一步明確，從而進一步闡釋不穩定性特征對翼尖渦流動的作用機制。因此，本文通過SPIV(Stereo Particle Image Velocimetry)試驗技術測量不同雷諾數、迎角下的翼尖渦流場，得到了翼尖渦搖擺運動的特征及演化過程；進一步地，通過線性穩定性分析研究了雷諾數和迎角對翼尖渦不穩定性的影響，并求解其不穩定性隨流向的演化過程和擾動模態。在此基礎上，分析了翼尖渦的不穩定性特征與搖擺運動的關系，闡釋了翼尖渦搖擺運動的產生機制，從而為這類流動的非定常流控策略提供參考。

1 試驗方法與后處理計算

1.1 SPIV試驗方法

試驗在低速回流式風洞中進行，最大風速為70 m/s，試驗段尺寸為1.2 m×0.9 m。收縮段前安裝蜂窩網以降低試驗段的湍流度，試驗中的湍流度為0.2%。使用NACA0015等直翼產生翼尖渦，機翼弦長c= 0.203 m，展弦比AR=5。試驗過程中，機翼安裝在一個與風洞內壁面底部固定的轉盤上以實現迎角的調節。測試迎角為α=4°,8°,10°；來流速度U∞=15,20,25 m/s，對應基于弦長c的雷諾數分別為Re=2.1×105,2.8×105,3.5×105；尾跡區內翼尖渦流場的測量范圍x/c=0.6～6.0，等距離分布共計10個截面，其中x為流向坐標。

翼尖渦流場通過SPIV獲得，通過大小為1～5 μm 的乙二醇小油滴對流動進行示蹤。激光光源選用Nd:YAG雙脈沖激光發射器，對流場進行顯示。試驗所用激光的雙脈沖能量為2×380 mJ，雙脈沖頻率為1 Hz，激光波長為532 nm，兩次脈沖間隔為10 μs，片光源的厚度為2 mm并垂直于來流方向。使用2臺型號為Imager-Pco的高分辨率CCD相機對激光片光源照射的流場截面進行拍攝，相機夾角為90°，如圖1所示。試驗中圖像采集的分辨率為2 048 pixel×2 048 pixel，采樣頻率同步為1 Hz，通過532 nm波長帶通濾光鏡來提高圖像信噪比。為了得到翼尖尾跡區內不同截面的翼尖渦結構，可通過導光臂調節激光器所發射片光源在流向的位置。對每個截面采集200 s流場數據，并通過TSI INSIGHT 4G軟件對圖像進行配對和解算，其解調范圍為24 pixel×24 pixel，有效重疊率為50%，得到翼尖渦流場在x、y、z這3個 方向的速度，并計算得到渦量場。

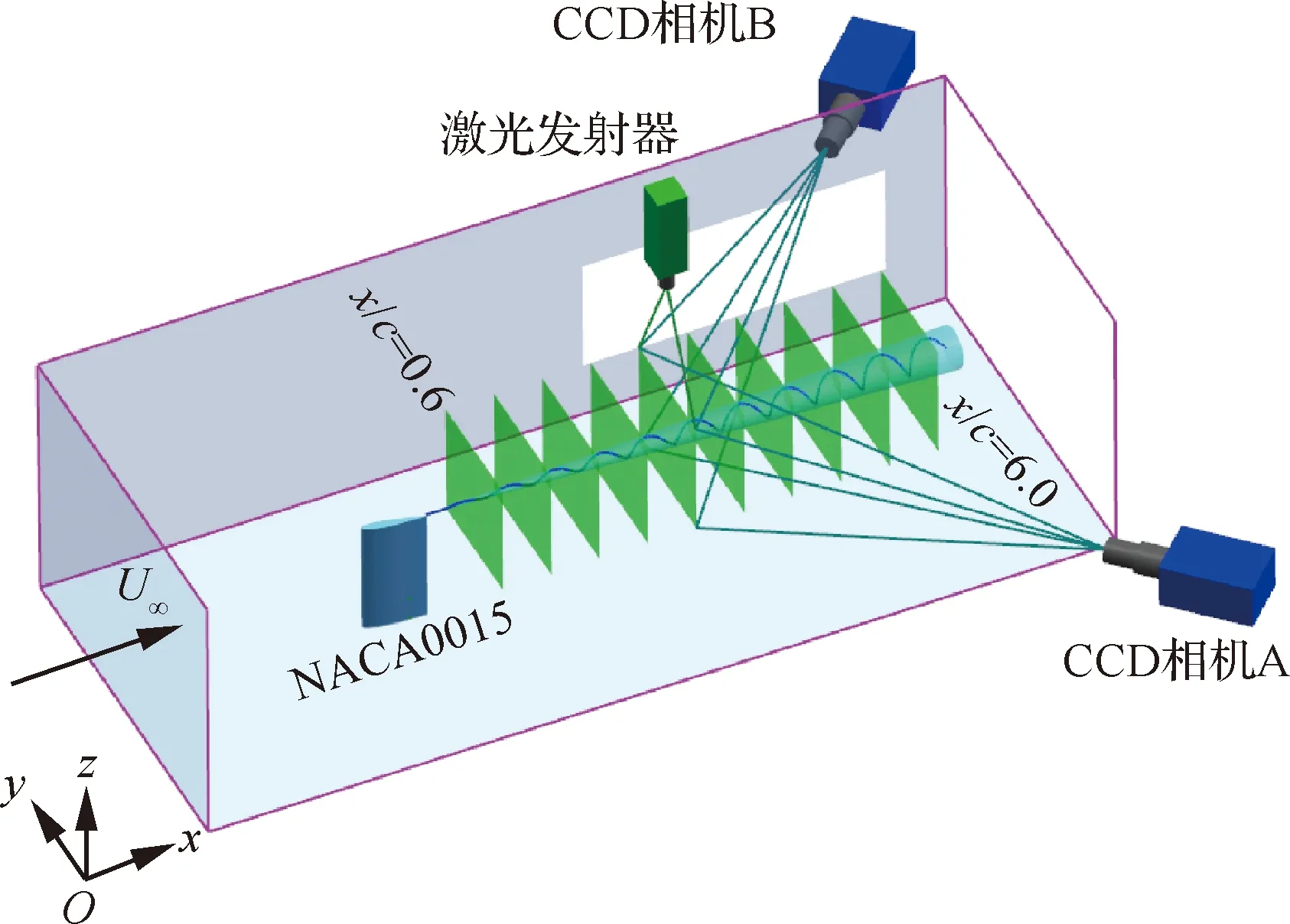
圖1 SPIV試驗設置示意圖Fig.1 Schematic of SPIV experimental setup

1.2 試驗后處理計算

通過瞬時渦核位置表征翼尖渦在搖擺過程中各個時刻的位置。由于翼尖渦搖擺運動的影響，以切向和徑向速度最小位置確定的渦核位置不準確，因此本研究中以渦量一階原點矩的方法確定翼尖渦的瞬時渦核位置：

(1)

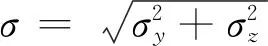
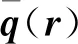
(2)

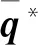
2 翼尖渦搖擺特征

計算各截面的SPIV流場瞬時渦核位置，獲得翼尖渦在不同截面的瞬時渦核分布，如圖2所示。由圖2可知，α=8°,U∞=25 m/s條件下近場(x/c= 1.2)瞬時渦核的分布近似各向同性，隨著翼尖渦向下游傳輸，搖擺幅值逐漸放大，且渦核分布逐漸呈現出各向異性特征，相關系數e也反映了各向異性特征隨流向逐漸增強的趨勢。比較試驗測得的瞬時渦核在y、z方向的分布與根據平均渦核位置和σy、σz確定的高斯分布，可見兩者精確符合。高斯分布描述的瞬時渦核分布定量地反映了以上翼尖渦搖擺規律，即搖擺幅值隨流向逐漸增大，并且σy>σz。

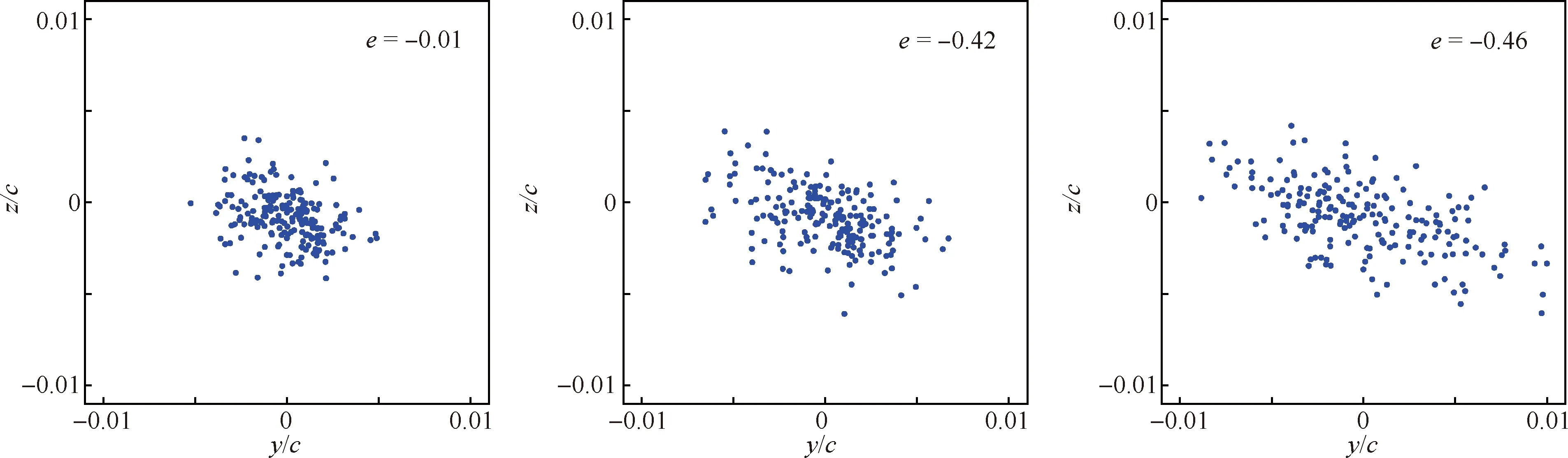
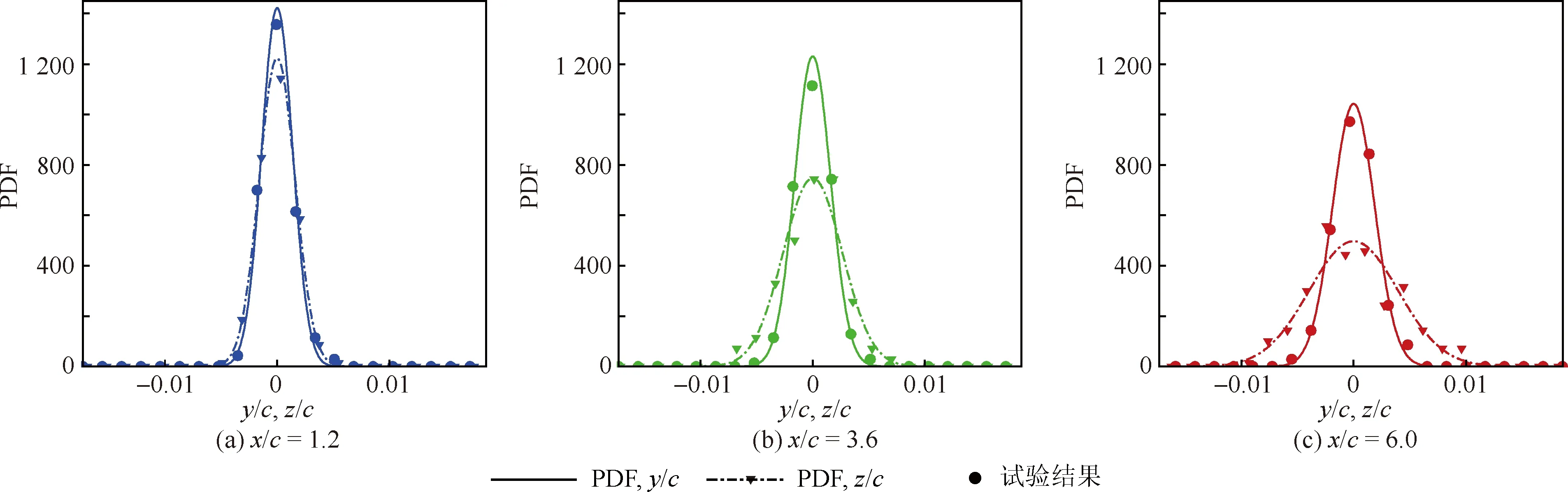
圖2 α=8°,U∞ = 25 m/s工況下的瞬時渦核分布和其概率密度函數(PDF)分布Fig.2 Distribution of instant vortex core at α=8°,U∞ = 25 m/s and corresponding probability density function distribution

2.1 翼尖渦搖擺幅值變化

計算各工況下翼尖渦搖擺幅值沿流向x的變化，使用當量渦核半徑rc對其無量綱化，如圖3所示，可以發現搖擺幅值在各種條件下均隨流向有逐漸放大的趨勢。此外，4°迎角下翼尖渦搖擺幅值顯著大于8°和10°迎角；并且8°和10°迎角下搖擺幅值隨流向增長相對于4°迎角明顯更為迅速。造成這種現象的原因是不同流動狀態的翼尖渦穩定性存在差異，外界擾動在4°迎角條件下不易發展，因此搖擺幅值增長較為緩慢，進一步的定量化解釋可參見第4節中的線性穩定性分析結果。比較雷諾數對翼尖渦搖擺幅值的影響，可以發現試驗中在Re=2.1×105,2.8×105,3.5×105條件下各迎角的翼尖渦搖擺幅值基本處在同一范圍。

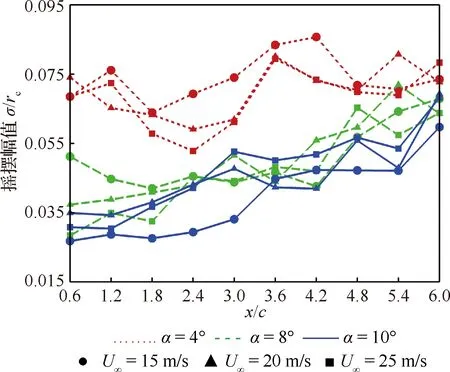
圖3 翼尖渦搖擺幅值σ隨流向x的演化Fig.3 Streamwise evolution of wingtip vortex wandering amplitude σ along x

需要指出的是，翼尖渦搖擺幅值雖然沿流向總體表現出放大趨勢，但其過程中可能存在波動，如在Re=2.8×105和Re=3.5×105條件下，x/c=2.4截面的翼尖渦搖擺半徑存在局部減小的情況。因此，取單一截面研究翼尖渦搖擺幅值隨迎角、雷諾數變化得到的結果可能不準確[26]，應當從翼尖渦在尾跡區內演化的整體角度對翼尖渦搖擺運動進行研究。

2.2 翼尖渦瞬時渦核分布

在2.1節中已對翼尖渦搖擺的特征及其搖擺幅值隨流向演化進行了闡述，為了更直觀地描述翼尖渦搖擺運動隨流向的變化規律，并顯示翼尖渦隨流向運動軌跡，計算x/c= 1.2,3.6,6.0的瞬時渦核分布在各迎角和來流速度條件下的聯合概率密度(JPDF)分布。圖4清晰地顯示了渦核由近場的集中分布，沿流向逐漸發展為十分離散的分布，并且在機翼法向搖擺幅值更大，即具有明顯的各向異性特征，搖擺運動的方向與Iungo等的試驗結果[16]一致。

圖5顯示了各個雷諾數和迎角下渦核位置聯合概率密度分布沿流向的演化過程。從圖5(a)可以觀察到，在4°迎角下翼尖渦搖擺的幅度基本隨流向保持一致，表現為較緩慢的增長；而在8°迎角和10°迎角條件下，翼尖渦搖擺運動幅值顯著增大。此外，翼尖渦在沿流向演化過程中逐漸表現出明顯的各向異性，并且在大迎角條件下更為顯著。由圖5(b)和圖5(c)中的x/c=6.0截面可觀察到，在8°和10°迎角下機翼法向的搖擺運動明顯相比于展向的運動更為劇烈，而在4°迎角下這種各向異性并不十分明顯。

綜上所述，試驗結果表明，翼尖渦在各試驗工況下均存在搖擺運動，其搖擺幅值隨迎角增大而減小；但是在8°與10°迎角條件下，搖擺幅值隨流向x的增長率相比于4°則明顯更大，即在大迎角條件下，搖擺幅值的流向增長率更大；同時，翼尖渦搖擺的各向異性特征隨流向x方向逐漸增強。

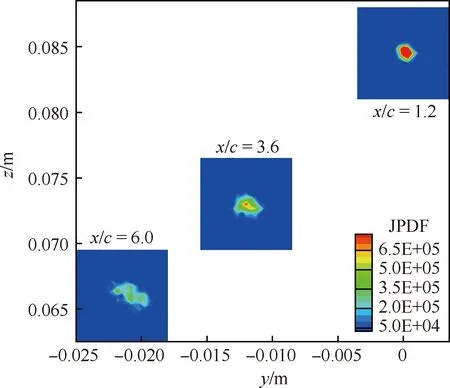
圖4 渦核位置聯合概率密度分布(α= 10°,U∞ = 25 m/s)Fig.4 JPDF distribution of vortex core at α = 10°,U∞ = 25 m/s

3 線性穩定性分析方法

3.1 擾動方程

為了對翼尖渦搖擺產生機制進行更深入的研究，使用線性穩定性分析求解翼尖渦的不穩定性演化過程和不穩定模態。通過求解線性化的小擾動Navier-Stokes方程，可以定量地得到反映流動不穩定性特征的相應參數。本研究中使用柱坐標系(r,θ,x)下的擾動方程形式，其中各瞬時流動變量可寫為

q=[ur,uθ,ux,p]T

(3)

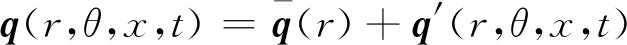
(4)

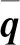
q′(r,θ,x,t)=[ur′,uθ′,ux′,p′]T=

(5)

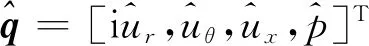
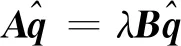
(6)

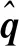
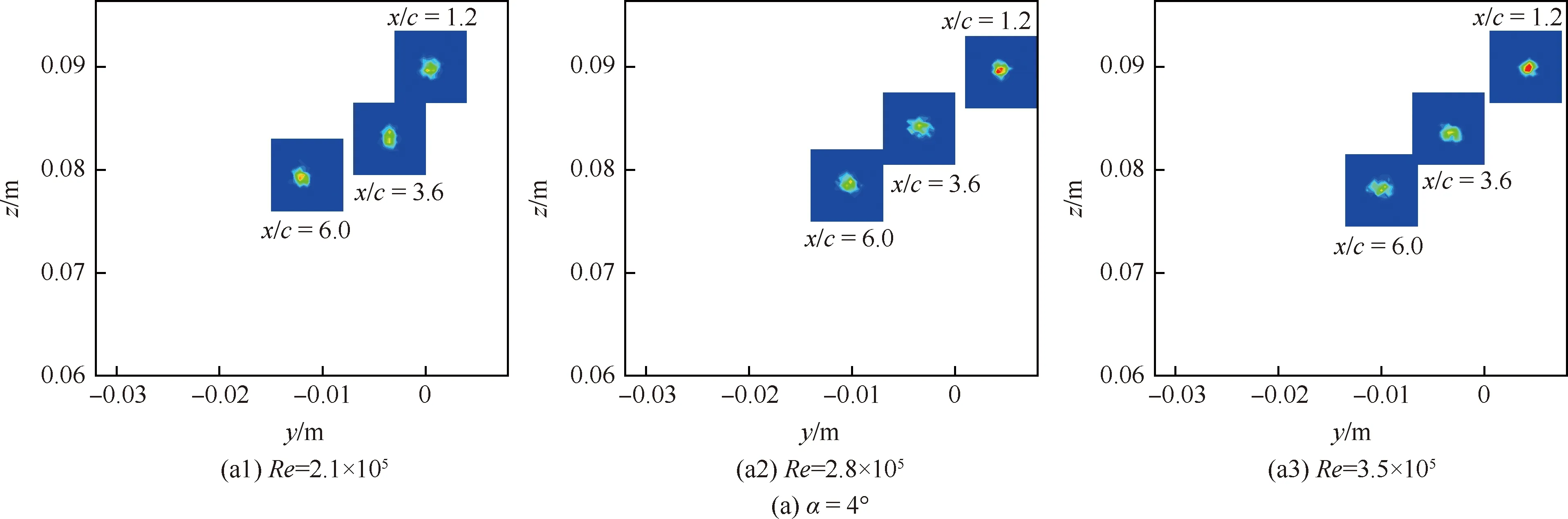
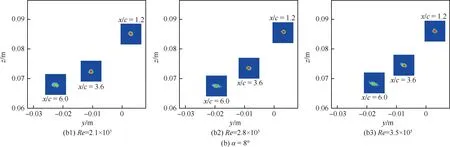
圖5 不同雷諾數和迎角條件下渦核聯合概率密度分布隨流向演化(云圖范圍為[0.5×105,7.5×105])Fig.5 Streamwise evolution of joint probability density distribution of vortex cores at different Re and α (Contour range:[0.5×105,7.5×105])

3.2 程序驗證

在求解試驗測量的翼尖渦流場的穩定性特征之前，分別通過3個時間不穩定性算例和2個空間不穩定性算例對本文所使用的求解流動穩定性的方法和程序的準確性予以驗證，算例包含圓管中的Poiseuille流和Batchelor渦等典型流動。

3.2.1 時間不穩定性

對圓管中Poiseuille流分別計算了Re=200和Re=2 200條件下的時間不穩定性，周向波數n=1，流向波數β= 1；在此基礎上對角速度Ω為0.1的管壁旋轉運動予以驗證，計算條件為：Re=100，β=0.5,1.0，n=0，Ω、β、n均為無量綱量。計算結果與文獻比較如表1和表2所示。從表1和表2中的對比結果可以發現，文中方法對Poiseuille流的時間不穩定模態的特征值能夠實現準確求解。

進一步計算Re=141.4，β= 1.34條件下旋擰度在0.1～1.4范圍內的尾跡渦穩定性，其中包含兩個較不穩定的模態，與文獻[20]比較如圖6所示。從圖中可以看出對于一階不穩定模態和二階不穩定模態，本文中使用的方法與文獻結果符合較好。

表1 圓管Poiseuille流時間不穩定性結果(n = 1,β = 1)與文獻[20]比較Table 1 Comparison of temporal instability results of Poiseuille flow (n=1,β=1)in a pipe with Ref.[20]

表2 旋轉圓管Poiseuille流時間不穩定性結果與文獻[20]比較(Re=100,n=0)Table 2 Comparison of temporal instability result of Poiseuille flow in a rotating pipe with Ref.[20](Re=100,n=0)

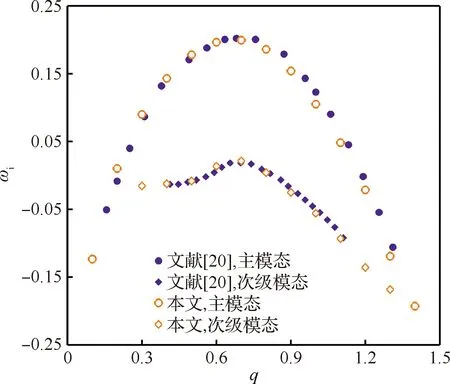
圖6 尾跡渦時間不穩定性與文獻[20]比較Fig.6 Comparison of temporal instability of trailing vortex with Ref.[20]

3.2.2 空間不穩定性

對圓管中的Poiseuille流進行空間不穩定性計算，計算條件為：雷諾數Re=10 000，頻率ω= 0.5，周向波數n分別為0和1，與文獻結果比較如表3所示。進一步計算Batchelor渦的空間不穩定性以對程序進行驗證，條件分別為Re=667、n=-1、ω=-0.15,旋擰度為0.7和Re=108、n=-1、ω=-2.75，旋擰度為3，與文獻結果比較如表4所示。

表3和表4的結果表明，研究使用的方法可以精確計算求解大范圍雷諾數條件下的Poiseuille流和Batchelor渦的空間不穩定性，為之后的研究奠定了基礎。

表3 圓管Poiseuille流空間不穩定性結果與文獻[20]比較Table 3 Comparison of spatial instability results of Poiseuille flow in a pipe with Ref.[20]

表4 Batchelor渦空間不穩定性結果與文獻[20]比較Table 4 Comparison of spatial instability result of Batchelor vortex with Ref.[20]

4 翼尖渦不穩定性對搖擺運動作用機制

4.1 翼尖渦線性穩定性分析

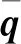
由于流場的擾動是不同頻率、波數的擾動分量的疊加[12]，因此需要尋找在何種頻率、波數下，由特征值譜得到的擾動主模態隨空間或時間的放大率最大，由此確定翼尖渦的空間與時間不穩定性。圖8顯示了x/c=4.8,α=10°,U∞=25 m/s條件下，不同擾動波數β的擾動主模態的時間放大率ωi關于β的變化曲線。ωi-β曲線的每一個點均反映了時間不穩定性特征值譜的擾動主模態在對應的擾動波數β下的時間放大率，例如圖8的插圖即為β=0.3的時間不穩定性特征值譜，擾動主模態的特征值由方框標出。由ωi-β曲線的極值點可得，波數β=0.295的擾動主模態的時間放大率最大，因此該極值點所對應的就是該截面與工況下翼尖渦的時間不穩定性模態，放大率為ωi= 5.71×10-5。對于空間不穩定性分析，計算具有不同頻率ω的擾動主模態的空間放大率-βi關于ω的變化曲線，-βi的極大值和其對應的ω即為翼尖渦在該工況、該截面的空間不穩定性放大率和擾動頻率。

對其他截面的流場作相同的處理，可以得到不同流動條件與流向截面的翼尖渦的空間與時間不穩定性、不穩定性放大率以及對應的擾動頻率的演化過程。

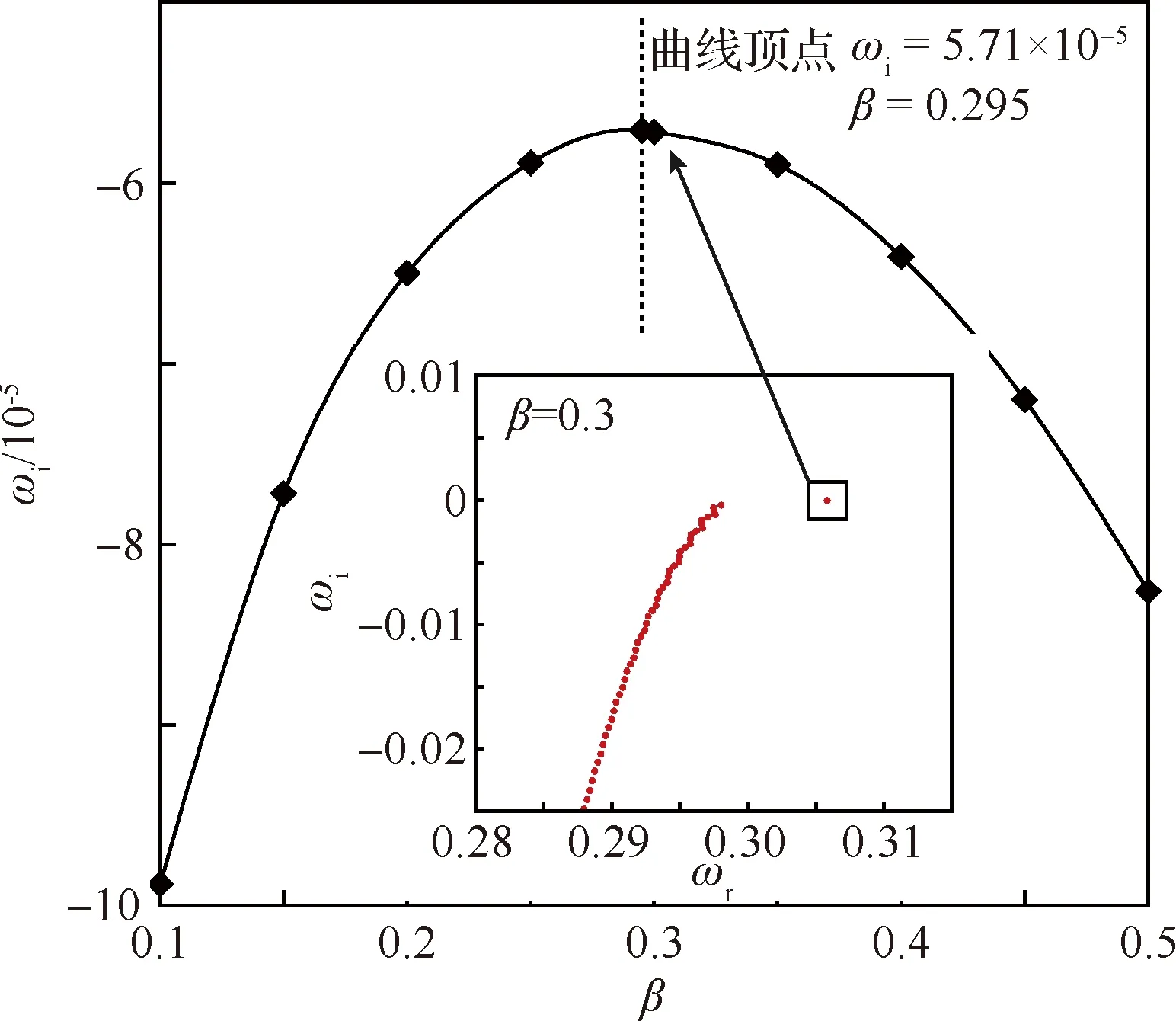
圖8 x/c=4.8、α=10°、U∞=25 m/s條件下，時間不穩定性擾動主模態的放大率ωi與其擾動波數β的變化曲線(插圖為β=0.3的時間不穩定性特征值譜，小方框中為其擾動主模態的特征值)Fig.8 Variation of growth rate ωi of temporal primary mode with its streamwise wavenumber β at x/c=4.8，α=10°，U∞=25 m/s (the inset being the eigenvalue spectrum of temporal instability at β= 0.3,with eigenvalue in the box corresponding to its primary mode)

4.2 翼尖渦不穩定性特征演化

對各個工況下翼尖渦時間和空間不穩定性放大率進行計算，得到不穩定性放大率關于流向x的變化規律，如圖9所示。結果表明，在試驗測量的各工況下，翼尖渦在所測量的尾跡區范圍內(x/c=0.6～6.0)的時間/空間不穩定性放大率ωi和-βi均小于0，意味著翼尖渦在所測量的條件下均處于臨界穩定狀態。因此在試驗觀察中，翼尖渦沒有發生失穩和破碎現象。但是，翼尖渦不穩定性放大率沿流向均呈現出放大趨勢，隨著翼尖渦在遠場(10倍展長以外的區域)的衰減，不穩定性將占據主導作用[1]，從而導致翼尖渦在遠場發生失穩甚至破碎現象。受試驗段長度的限制，后續研究中需對更遠處的尾跡截面進行測量，以對此予以驗證。

進一步分析雷諾數與迎角對翼尖渦空間不穩定性的影響，如圖10所示，其中灰色區域示意了各工況下不穩定性放大率在流向x上的變化范圍。可發現隨著雷諾數的增加，不穩定性放大率逐漸增大，并且在迎角為8°和10°條件下的翼尖渦不穩定性明顯大于4°條件下的情況。圖9中雖然4°迎角下翼尖渦不穩定增大率隨流向增長較快，但幾乎始終小于8°與10°迎角下的增長率。

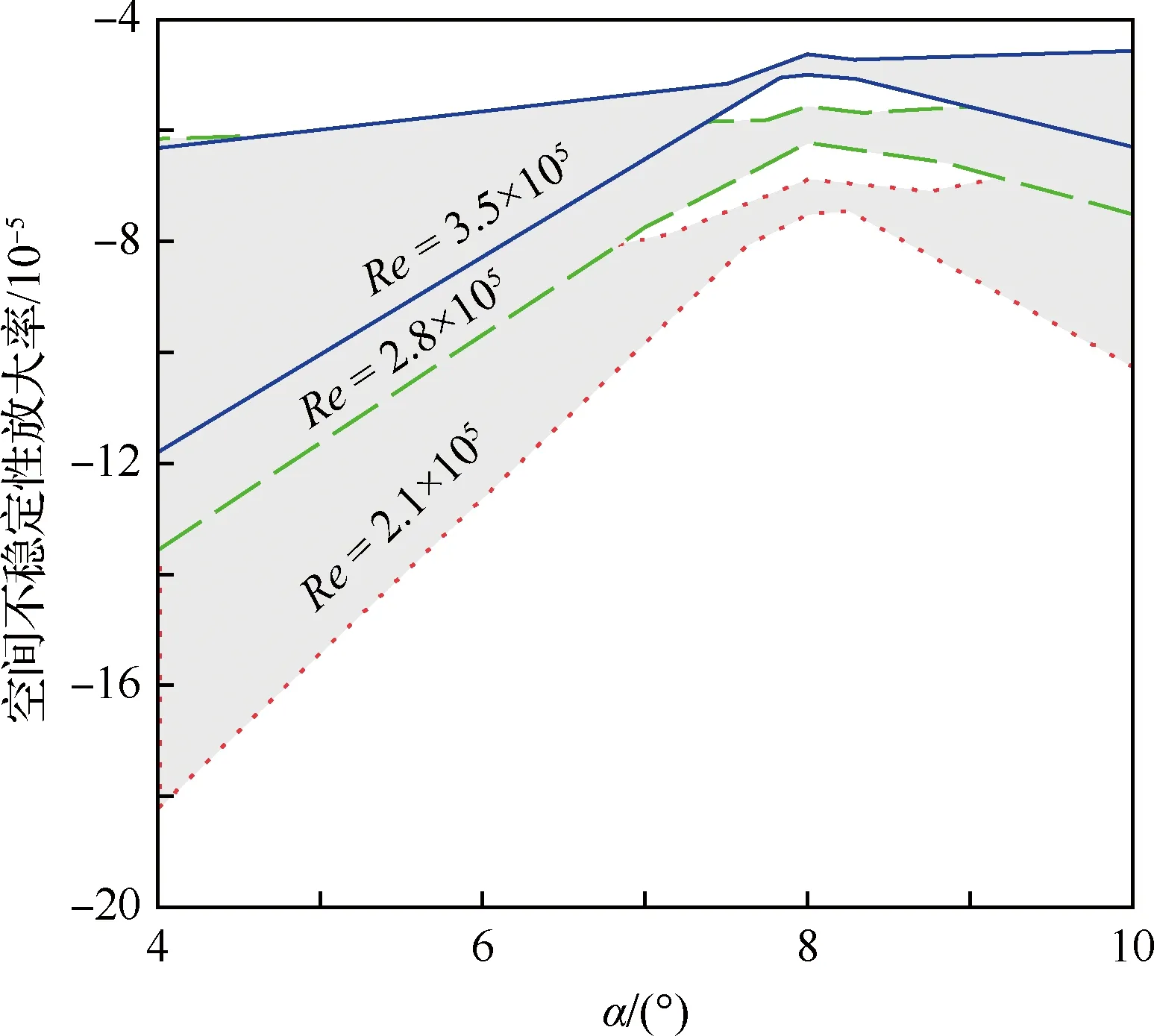
圖9 不同雷諾數條件下空間不穩定性放大率與迎角關系Fig.9 Spatial instability amplification ratio via angles of attack at different Reynolds numbers

圖10 空間/時間不穩定性放大率隨流向變化Fig.10 Streamwise evolution of spatial/temporalinstability amplification ratio

以上線性穩定性分析的結果解釋了2.1節中圖3所顯示的大迎角條件下搖擺幅值隨流向增長更迅速的現象。由于真實流動中的微小擾動客觀存在(其來源可能是風洞壁面或大氣環境等)，當翼尖渦受到擾動后，在小迎角條件下(4°)，因其自身空間不穩定性較弱，擾動不易隨流向放大，因此表現為渦搖擺幅值隨流向的緩慢增長；而在大迎角條件下(8°,10°)，翼尖渦自身空間不穩定性較強，擾動在空間上相對于小迎角條件更容易被放大，因此翼尖渦搖擺的幅度隨流向增大趨勢更為明顯。而由于各流向截面x的ωi<0，由流動上游傳輸的擾動將隨時間t不斷衰減，因此試驗中各截面的翼尖渦未發生破碎，而是僅表現出包含有主導頻率的搖擺運動。

4.3 翼尖渦搖擺波數與頻率

通過線性穩定性分析還可以得到翼尖渦不穩定模態在空間與時間上的無量綱波數βr和頻率ωr，如圖11所示。在沿流向發展過程中，擾動的無量綱擾動波數βr與頻率ωr均有所減小，并且相同雷諾數條件下8°與10°迎角的擾動頻率基本小于4°迎角；當雷諾數增加時，擾動頻率有所增加，薛棟[8]通過水槽試驗也得到了相似的規律。

此外，在測量范圍內的各尾跡截面下，翼尖渦擾動無量綱波數βr與頻率ωr均十分接近。由此可知，在試驗測量的流動條件下，翼尖渦擾動的無量綱相位速度接近于1，即擾動的相位速度和自由來流速度U∞基本一致，Edstrand等使用Bi-Global LSA對翼尖渦的穩定性分析也得到了相似的結果[25]。這與平面Poiseuille流中擾動的無量綱相位速度小于2/3的結果截然不同[29]，其原因是試驗測量的翼尖渦并不包含任何類似Poiseuille流中的邊界層結構而限制擾動的傳遞。與Poiseuille流不同，翼尖渦流向速度基本接近自由來流速度，基于臨界層理論[30]，其擾動相位速度也因此明顯大于Poiseuille流。此外根據Gaster變換-ωi/βi=?ωr/?βr=vg[31]，還可以得到擾動的群速度vg，即擾動波包的傳輸速度。由圖9中翼尖渦在各尾跡截面的時間與空間不穩定性放大率較為接近的結果，可以得出擾動群速度vg≈1，這也與圖11所示ωr和βr的結果一致。擾動群速度近似為1的結果意味著擾動的波包將向下游傳輸，因而試驗中翼尖渦的不穩定性特征是對流的而非絕對的[30,32]：隨著擾動向下游的發展，翼尖渦會在遠場的某一截面位置發生失穩；但擾動不會同時向上游傳輸而使翼尖渦隨時間發生全局的破碎，這與試驗中x/c=0.6～6.0的范圍內翼尖渦在200 s的觀測時間內均未發生破碎的現象相符合。

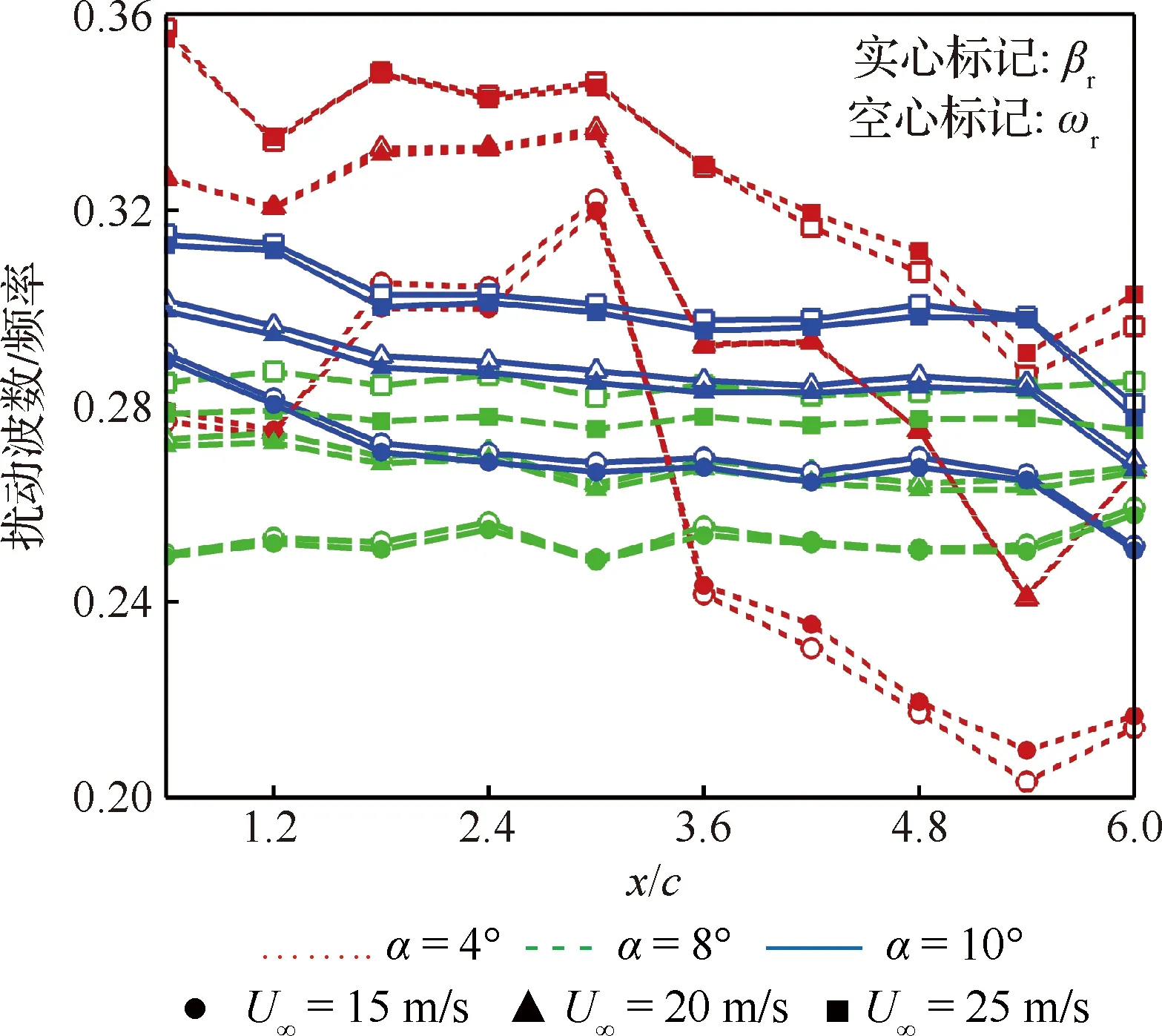
圖11 不同工況下擾動波數與頻率隨流向變化Fig.11 Streamwise variation of perturbation wavenumber and frequency at different conditions

進一步由無量綱頻率ωr可得，各試驗工況下翼尖渦擾動的斯特勞哈爾數Sr均在0.045附近，根據無量綱參數c=0.203和來流速度U∞，可得到翼尖渦在U∞=15,20,25 m/s下的擾動頻率f分別為3.3、4.4、5.5 Hz，這與Devenport[5]和Bailey[9]等試驗測得的翼尖渦搖擺主導頻率可比。受限于試驗激光脈沖頻率為1 Hz，對于采集得到的翼尖渦渦核位置時間序列無法通過傅里葉變換得到其主頻率，因此后續需要提高試驗激光脈沖頻率以對計算得到的頻率進行驗證。

4.4 翼尖渦搖擺機制

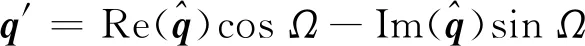
(7)

式中：Ω=βx+nθ-ωt，轉換到笛卡兒坐標系后可以得到速度擾動在x、y、z方向的分量u′、v′、w′的分布。

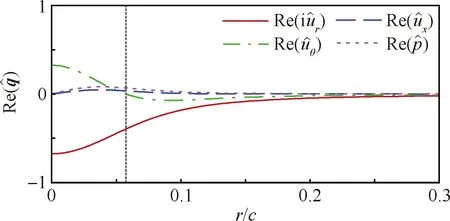
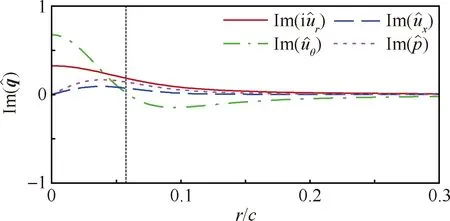
圖12 α=10°,U∞=20 m/s，x/c=6.0時翼尖渦空間的不穩定性擾動解(虛豎線為最大切向速度位置)Fig.12 Disturbance of spatial instability of wingtip vortex at α=10°,U∞=20 m/s，x/c=6.0(dashed vertical line indicating location of maximum tangential velocity)

進一步計算翼尖渦最不穩定模態的橫向合速度u′tr=[v′,w′]T，并考慮擾動隨時間t的相位變化。圖14顯示了在相位t= 0,T/4,T/2,3T/4下的u′tr分布與試驗測量的翼尖渦瞬時渦核分布的比較情況，其中T為擾動的時間周期，根據4.3節中計算的擾動頻率，在α=10°,U∞=20 m/s,x/c=6.0條件下，T=0.24 s。從圖14(b)和圖14(c)可以觀察到，橫向擾動速度u′tr在其各個相位都具有明顯的方向性，并且集中于渦核位置，圖中箭頭示意了u′tr在渦核附近速度矢量的連線；由u′tr在各相位的分布可以發現，橫向擾動速度u′tr隨時間t呈現周期性的旋轉。不穩定性特征引起的橫向速度擾動u′tr的方向性以及周期性旋轉共同導致了翼尖渦的搖擺運動，表現為圖14(a)中試驗測量的渦核在兩個方向上均存在搖擺運動分量，并且搖擺運動含有主導頻率，是翼尖渦產生搖擺運動的內在原因。圖14(a)中箭頭示意了搖擺運動的主軸，其長度表征了搖擺幅值，雖然由LSA得到的擾動模態隨時間t僅僅表現為周期性旋轉，但由兩個主軸方向的搖擺幅值可得，該條件下的翼尖渦搖擺運動仍具有各向異性特征，其原因可能有以下幾種。首先，作為擾動的外在來源之一，自由來流中的湍流在各方向非均勻[9]，使特定相位的不穩定模態速度擾動受到放大或抑制，引起搖擺運動在不同方向的幅值產生偏差；其次，渦核區域的湍流小渦結構受到翼尖渦自身的拉伸作用會產生各向異性的雷諾正應力[33-34]，進一步誘導翼尖渦搖擺發生各向異性。然而，作為翼尖渦搖擺的內在原因，橫向擾動速度在各相位所具有的方向性特征仍是搖擺運動發生各向異性的前提，其具體成因則還有待更進一步的分析與研究。

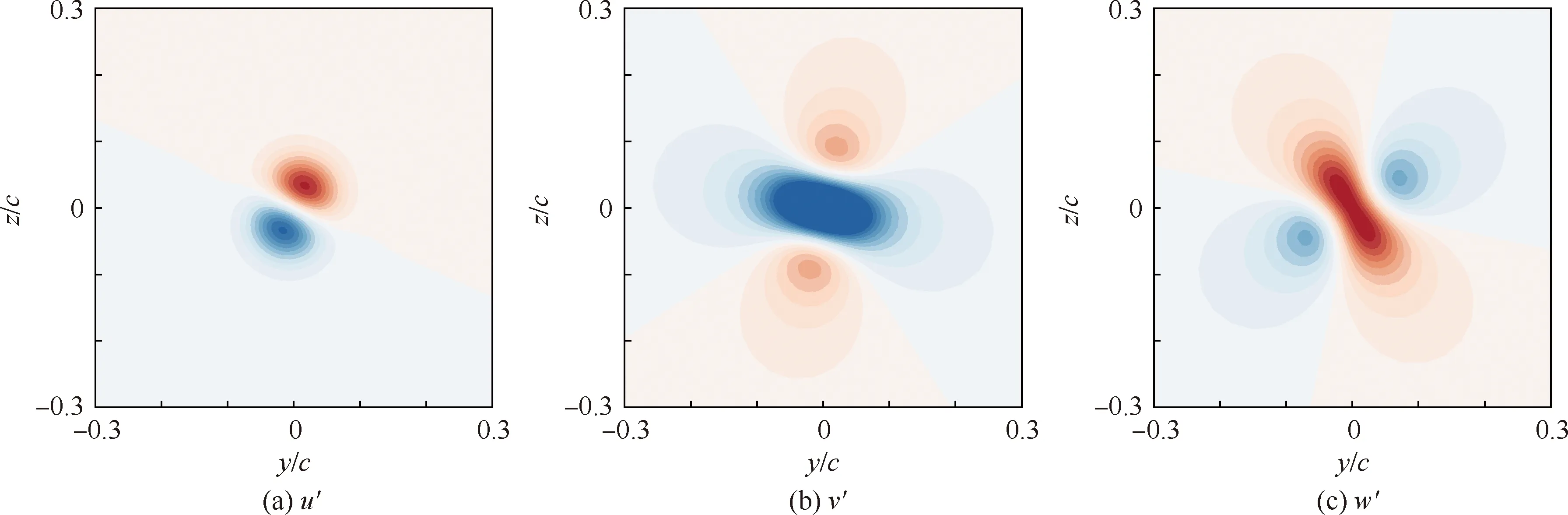
圖13 α=10°,U∞=20 m/s，x/c=6.0時翼尖渦最不穩定模態的u′、v′、w′云圖(v′、w′的云圖范圍為[-0.3,0.3]，u′的云圖范圍為[-0.1,0.1])Fig.13 Contours of u′,v′,w′ of the most unstable mode of wingtip vortex at α=10°,U∞=20 m/s，x/c=6.0 (range of v′,w′ :[-0.3,0.3],and range of u′:[-0.1,0.1])

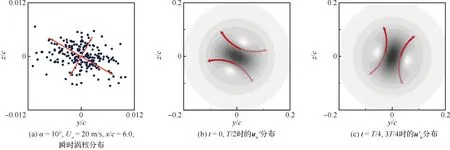
圖14 試驗測量的瞬時渦核分布與LSA計算的擾動模態比較Fig.14 Comparison between experimental instantaneous vortex core distribution and disturbance mode by LSA

由此，根據翼尖渦最不穩定擾動模態及其相位變化與試驗測量得到的翼尖渦搖擺運動方向的匹配關系，可以進一步證明翼尖渦的穩定性特征是其搖擺運動的內在原因，其擾動模態決定了所呈現出的搖擺運動特征：渦核區域的橫向擾動速度u′tr具有明顯的方向性，誘導翼尖渦發生搖擺運動；u′tr的方向隨相位的周期性變化則使翼尖渦搖擺有別于一維的隨機振蕩，而是表現為在各方向均含有分量且具有主頻的搖擺運動。

5 結 論

通過SPIV試驗觀察翼尖渦的搖擺現象，得到了其搖擺幅值隨流向放大并且具有各向異性的特征，進而使用線性穩定性分析對搖擺運動修正后的翼尖渦進行研究，定量得到其穩定性、搖擺頻率和時間/空間的不穩定性放大率隨流向變化，以及這些特征與雷諾數和迎角的關系，揭示了翼尖渦不穩定性的演化規律，并闡釋翼尖渦搖擺機理以及穩定性對翼尖渦流動的影響機制。

1)各工況下翼尖渦搖擺幅值均沿流向放大，且搖擺運動在大迎角條件下在遠場具有明顯的各向異性，由近場的各向同性特征隨流向逐漸發展為機翼法向的搖擺幅值明顯大于展向搖擺幅值的各向異性特征。

2)翼尖渦受到擾動后，其不穩定性模態決定所表現出的搖擺運動特征，而其不穩定性決定擾動隨時間/空間的放大速率。翼尖渦在4°迎角下的不穩定性放大率明顯小于8°和10°迎角，即翼尖渦在大迎角條件下更不穩定，這是導致大迎角時搖擺幅值隨流向迅速增長的原因。

3)各試驗工況下翼尖渦擾動的斯特勞哈爾數在0.045附近，擾動頻率約為3～5 Hz。由時間與空間不穩定性分析結果得出擾動的群速度約為1，擾動將向下游發展，因此試驗中的翼尖渦表現出對流不穩定性特征。

4)由線性穩定性分析得到的翼尖渦不穩定模態，發現翼尖渦的速度擾動局限在渦核區域內，其在渦核處的橫向速度擾動具有明確的方向性，并且隨相位變化作周期性旋轉，這是導致翼尖渦發生搖擺運動的原因所在。

致 謝

感謝王笑、秦蘇洋、王煜凱和李林穎在試驗和論文撰寫過程中提供的幫助與寶貴意見。