基于有限元法–正交球面波源邊界點法的振動體聲學(xué)靈敏度分析

王文璟

摘 ? ?要：建筑噪聲是環(huán)境噪聲污染的一個主要來源，解決建筑噪聲輻射問題的根本途徑是從噪聲源入手控制噪聲的產(chǎn)生，也就是對建筑設(shè)備進(jìn)行低噪聲設(shè)計.因此，必須對噪聲源進(jìn)行量化的聲學(xué)靈敏度分析，以便為設(shè)計提供優(yōu)化方向.本文提出基于有限元法-正交球面波源邊界點法的聲學(xué)靈敏度計算方法，用于振動體的輻射聲場對振動體的材料和結(jié)構(gòu)幾何參數(shù)等設(shè)計變量的靈敏度計算.該方法避免了有限元-邊界元法存在的系數(shù)矩陣奇異積分、數(shù)值求積和非唯一性問題，從而降低了設(shè)計計算的難度.數(shù)值計算結(jié)果表明了所提分析方法的正確性與可行性.

關(guān)鍵詞：建筑噪聲;靈敏度分析;正交球面波源邊界點法;有限元法

中圖分類號：TU112 ? ? ? DOI：10.16375/j.cnki.cn45-1395/t.2019.03.009

引言

解決建筑噪聲問題的根源在于抑制固體振動源的聲輻射[1]，而控制聲輻射最有效的方法是對振源結(jié)構(gòu)的材料屬性和幾何形狀等參數(shù)進(jìn)行優(yōu)化設(shè)計以降低聲輻射.為了實現(xiàn)這一目標(biāo)，不但需要預(yù)測振動體的輻射聲場，還需要計算輻射聲場對振動體的材料屬性和幾何形狀的靈敏度，用于指導(dǎo)噪聲環(huán)境的優(yōu)化設(shè)計.

有限元[2-4]和邊界元法[5-8]是目前用于振動體聲學(xué)靈敏度分析的兩種主要方法，國內(nèi)外學(xué)者已經(jīng)相繼建立了多種基于上述兩種方法的聲學(xué)靈敏度分析方法[9].實際上，對于聲學(xué)問題來說，由于計算域的無界特性，邊界元法是更適合用于聲學(xué)靈敏度分析的算法.但是，由于邊界元法的系數(shù)矩陣需通過數(shù)值積分計算，同時還存在奇異積分處理和非唯一性等問題，導(dǎo)致邊界元法的計算復(fù)雜并且計算效率較低.將邊界元法用于聲學(xué)靈敏度計算時，需要對系數(shù)矩陣進(jìn)行求導(dǎo)，導(dǎo)致計算的復(fù)雜度進(jìn)一步增加.鑒于上述局限性，有學(xué)者提出了基于正交球面波源邊界點法的聲學(xué)靈敏度分析方法[10-12].該方法避免了邊界元法存在的問題，降低了數(shù)值處理難度并提高了計算效率.在目前的基于正交球面波源邊界點法的聲學(xué)靈敏度計算方法中，作為輸入量的結(jié)構(gòu)頻率響應(yīng)和結(jié)構(gòu)靈敏度是通過近場聲全息重建得到.由于近場聲全息本質(zhì)上是一種測試技術(shù)，因此目前的方法只適合用于已經(jīng)完成制造安裝的結(jié)構(gòu)的聲學(xué)靈敏度分析.但是，聲學(xué)靈敏度分析更重要的應(yīng)用場合是在設(shè)計過程，在設(shè)計階段實現(xiàn)噪聲輻射的優(yōu)化和控制能夠降低成本和縮短開發(fā)過程.

針對目前基于正交球面波源邊界點法的聲學(xué)靈敏度計算方法存在的局限性，本文將該方法與有限元法相結(jié)合.其中，有限元法用來計算振動體的結(jié)構(gòu)振動頻率響應(yīng)以及結(jié)構(gòu)振動對設(shè)計變量的導(dǎo)數(shù)，這些結(jié)構(gòu)響應(yīng)和導(dǎo)數(shù)計算結(jié)果作為正交球面波源邊界點法的輸入?yún)?shù)進(jìn)一步計算振動體輻射聲場對結(jié)構(gòu)設(shè)計變量的聲學(xué)靈敏度，從而實現(xiàn)振動體聲輻射靈敏度的正向設(shè)計.

1 ? ?基于有限元法-正交球面波源邊界點法的聲學(xué)靈敏度

假設(shè)振動體表面[N]個結(jié)點（表示為[rsi]，[i]表示第[i]個結(jié)點）上的法向振速組成的向量為[vns]，則基于正交球面波源邊界點法[3]可得到聲場中點[r]處的聲壓[p（r）]為：

式（9）即為基于正交球面波源邊界點法的聲學(xué)靈敏度計算公式.在該公式中矩陣[v*ns]與結(jié)構(gòu)相關(guān)，因此該矩陣相對設(shè)計變量的導(dǎo)數(shù)不為零，該導(dǎo)數(shù)可以通過對式（2）求導(dǎo)得到.在已知表面法向振速[vns]及其導(dǎo)數(shù)的前提下，使用式（9）即可求得聲壓相對設(shè)計變量的靈敏度.在之前研究中[vns]及其導(dǎo)數(shù)是通過近場聲全息重建獲得，但是這種方式不適合用于正向的聲學(xué)優(yōu)化設(shè)計，為此本文將有限元法和正交球面波源邊界點法相結(jié)合，建立正向的聲學(xué)靈敏度計算方法.

對于簡諧激勵條件下的有阻尼強(qiáng)迫振動，其在頻域中的有限元方程為[12]：

2 ? ? 數(shù)值驗證

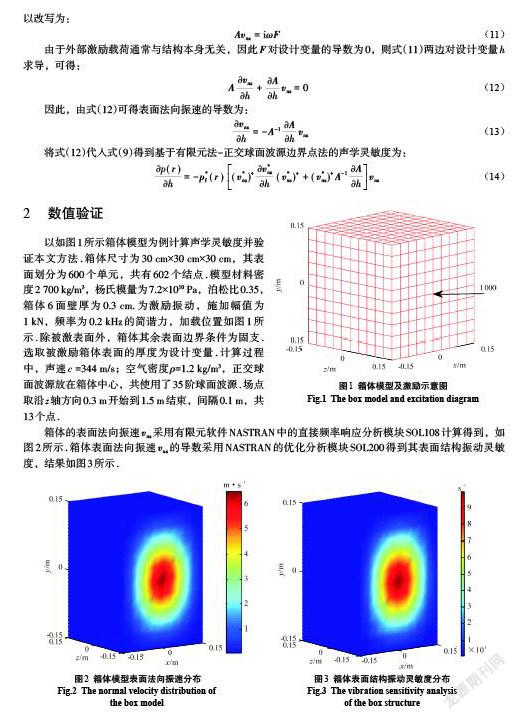
以如圖1所示箱體模型為例計算聲學(xué)靈敏度并驗證本文方法.箱體尺寸為30 cm[×]30 cm[×]30 cm，其表面劃分為600個單元，共有602個結(jié)點.模型材料密度2 700 kg/m3，楊氏模量為7.2[×]1010 Pa，泊松比0.35，箱體6面壁厚為0.3 cm.為激勵振動，施加幅值為 ? ? ?1 kN，頻率為0.2 kHz的簡諧力，加載位置如圖1所示.除被激表面外，箱體其余表面邊界條件為固支.選取被激勵箱體表面的厚度為設(shè)計變量.計算過程中，聲速[c=]344 m/s;空氣密度[ρ]=1.2 kg/m3，正交球面波源放在箱體中心，共使用了35階球面波源.場點取沿[z]軸方向0.3 m開始到1.5 m結(jié)束，間隔0.1 m，共13個點.

箱體的表面法向振速[vns]采用有限元軟件NASTRAN中的直接頻率響應(yīng)分析模塊SOL108計算得到，如圖2所示.箱體表面法向振速[vns]的導(dǎo)數(shù)采用NASTRAN的優(yōu)化分析模塊SOL200得到其表面結(jié)構(gòu)振動靈敏度，結(jié)果如圖3所示.

將求得的表面法向振速及其導(dǎo)數(shù)代入式（14），可以計算得到聲壓對該被激勵表面厚度的聲壓靈敏度.為驗證本文所提出方法的正確性，將本文方法計算所得結(jié)果與利用有限元差分法計算所得的結(jié)果進(jìn)行比較.有限差分法作為一種聲學(xué)靈敏度的有效計算方法，在應(yīng)用中收斂情況很大程度上依賴于差分步長，且為獲得設(shè)計變量改變后的聲學(xué)參量，需對有限元模型進(jìn)行多次修改，很大程度增加了計算量.有限差分法表達(dá)式為：

基于本文方法與有限差分法的計算結(jié)果如圖4所示.[Δh]分別取值1[×]10-4 m、1[×]10-5 m，由圖4可以看出，兩者計算結(jié)果基本相同.由圖5可看到計算結(jié)果相對誤差在[Δh]=1[×]10-4 m時，實部和虛部誤差基本大于10%，極值甚至達(dá)到了15%;而隨著差分增量[Δh]的減小，誤差隨之減小，當(dāng)[Δh]=1[×]10-5 m時，實部和虛部誤差幾近為1%，最大不超過2%，逐漸向基于有限元法-正交球面波源邊界點法的靈敏度計算結(jié)果收斂.從而說明了本文方法的正確性和可行性.

3 ? ?結(jié)論

本文將正交球面波源邊界點法和有限元法相結(jié)合，建立了聲學(xué)靈敏度分析方法.由于正交球面波源邊界點法的引入，規(guī)避了常用的邊界元法中系數(shù)矩陣的奇異積分、數(shù)值求積和非唯一性問題，大幅消除了數(shù)值處理工作的困難;與有限元法相結(jié)合，實現(xiàn)了振動體的輻射聲場對振動體的材料和結(jié)構(gòu)幾何參數(shù)等設(shè)計變量的靈敏度正向計算.數(shù)值計算結(jié)果表明了所提分析方法的正確性與可行性，以期能對建筑噪聲源的控制提供一定的優(yōu)化方向和量化依據(jù).

參考文獻(xiàn)

[1] 程芙榮.城市環(huán)境噪聲的治理[J].廣西工學(xué)院學(xué)報，2006，17（2）：107-110.

[2] HAGIWARA I，MA Z D. Development of eigenmode and frequency response sensitivity analysis methods for coupled acoustic-structure systems[J]. JSME International Journal Series，1992，35（2）：229-235.

[3] 張永斌，畢傳興，陳劍，等. 基于正交球面波源邊界點法的聲學(xué)靈敏度分析[J]. 機(jī)械工程學(xué)報，2007，43（2）：33-38.

[4] 陳立濤. 結(jié)構(gòu)聲學(xué)靈敏度計算方法研究[D].合肥：合肥工業(yè)大學(xué)，2013.

[5] 蔡俊，林瓊，蔡偉民. 用邊界元法研究不同頂端聲屏障的性能[J]. 噪聲與振動控制，2006（3）：89-91，109.

[6] ZHENG C J，MATSUMOTO T，TAKAHASHI T，et al. Explicit evaluation of hypersingular boundary integral equations for acoustic sensitivity analysis based on direct differentiation method[J]. Engineering Analysis with Boundary Elements， 2011，35（11）：1225-1235.

[7] ZHENG C J，MATSUMOTO T，TAKAHASHI T，et al. A wideband fast multipole boundary element method for three dimensional acoustic shape sensitivity analysis based on direct differentiation method[J]. Engineering Analysis with Boundary Elements，2012，36（3）：361-371.

[8] 張永斌，汪術(shù)龍，畢傳興，等. 預(yù)測聲屏障插入損失的拋物方程法及其初始聲場研究[J]. 聲學(xué)學(xué)報，2018，43（1）：69-75.

[9] 韓俊，向宇，陸靜.敷設(shè)被動約束層阻尼封閉箱體結(jié)構(gòu)聲振特征分析[J].廣西工學(xué)院學(xué)報，2012，23（1）：39-44.

[10] 張永斌，畢傳興，陳劍，等.基于正交球面波源邊界點法的聲學(xué)靈敏度分析[J].機(jī)械工程學(xué)報，2007，43（2）：33-38.

[11] 張永斌，畢傳興，陳劍，等.FFT在平面機(jī)械結(jié)構(gòu)聲學(xué)靈敏度分析中的應(yīng)用[J].農(nóng)業(yè)機(jī)械學(xué)報，2008，39（12）：216-218，173.

[12] 張永斌，畢傳興，陳劍，等.基于波疊加的結(jié)構(gòu)—聲學(xué)靈敏度分析的伴隨變量方法[J].機(jī)械工程學(xué)報，2009，45（4）：177-182.

Abstract： The construction noise is a main source of environmental noise. The effective way to control the construction noise is to make the noise sources generate less noise， i.e. controlling noise in the design stage. However， implementing low noise design of construction equipments requires more information that cannot be obtained empirically. Instead， the quantitative value of acoustic sensitivity is necessary for low noise design since it can provide the optimized orientation for low noise design of radiating structures. In the paper， the finite element method and orthogonal spherical wave source boundary point

method is combined for acoustic sensitivity analysis， by which sensitivity of acoustic quantities with respect to the design variables such as structural parameters and physical properties can be achieved precisely. Compared with the conventional method that combines the finite element method and boundary element method， the proposed method has no inherent problem of singular integration and non-uniqueness which will make numerical processing more complicated. The validity and feasibility of the proposed method is verified by numerical results.

Key words： construction noise; sensitivity analysis; orthogonal spherical wave source boundary point method; finite element method

（責(zé)任編輯：黎 ?婭）