非線性高維擾動Klein-Gordon方程的孤子波攝動解

徐建中　莫嘉琪

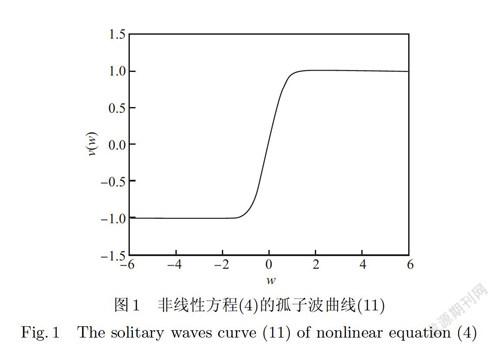
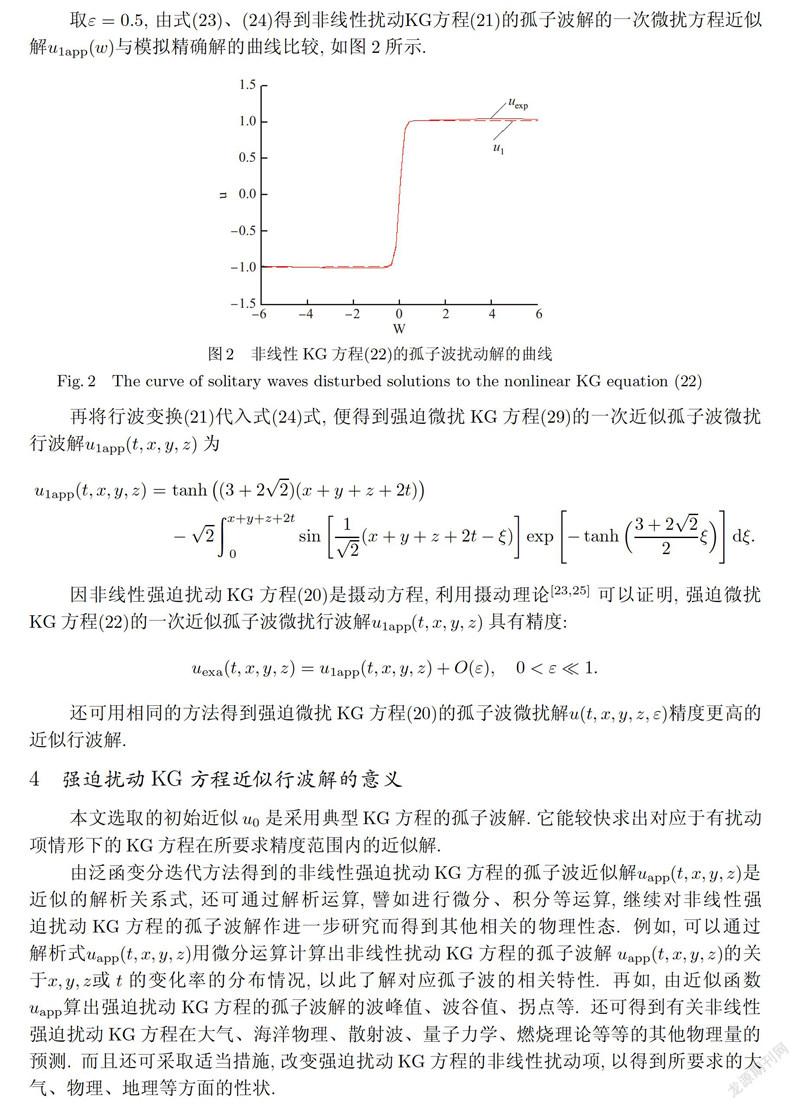
摘要：利用廣義變分迭代方法討論了一類非線性強迫擾動Klein-Gordon方程.首先，用雙曲函數待定系數法求得了無擾動方程孤子波.其次，利用泛函變分迭代原理得到了強迫擾動Klein-Gordon方程的一個攝動近似解.最后，論述了解的一致有效性.得到的近似解是解析式，它可對近似解進行解析運算，這對用簡單的模擬方法得到的近似解是達不到的.

關鍵詞：攝動解;孤子波;變分迭代

中圖分類號：0157.29

文獻標志碼：A

DOI： 10.3969/j.issn.1000-5641. 2019.06.003

0 引言

非線性孤子波理論在地球物理、光學、力學、理論物理學等學科中有很重要的應用.例如在地理科學、海洋物理、散射波、燃燒理論等方面，許多學者作了多方面的研究，如Salathiel等利用Riccati方程映射方法研究了電晶格孤子行波[1]，Yu等研究了Bose-Einstein冷凝體的孤子波[2]、 Chow等研究了K-折疊松散的Ricci孤子波[3]，等等[4-9].非線性孤子波理論的定量和定性方法已有很多的改進，非線性孤子波解的一種研究方法是擾動理論的近似方法，主要是用擾動理論的近似展開式將非線性孤子波方程轉化為易求解的方程來求解，這樣就擺脫了對于模擬數值方法的依賴.此方法的優點在于思路直接明了，計算簡單，可得到解的較高近似度.且求得的近似解具有解析性態，故不但能進行定量方面的分析，而且還能進行定性方面的分析.此方法使用面廣，具有較廣的研究前景，

作者等人利用廣義變分迭代、同倫映射、微分不等式和不動點理論等方法也研究了一些孤立波理論及有……