大學數學與專業課的相關性分析

李靜 萬波

摘要：通過對學生成績的統計分析和相關性檢驗可以看出，大學數學成績的好壞對專業課的影響是明顯的，具備較豐富的數學知識和較好的數學素養是專業學習和可持續發展的重要途徑.因此，在教學上應把握人才培養目標，從教育的高度認識大學數學教學，有效整合教學內容，踐行大學基礎數學教學為專業服務的理念.

關鍵詞：大學數學;專業課;多元線性回歸;相關性分析;可持續發展

中圖分類號：O13;G64? 文獻標識碼：A? 文章編號：1673-260X（2019）08-0005-03

1 引言

大學數學課程是高校大學生極其重要的公共基礎課，不僅為學生專業課的學習奠定堅實的數學知識基礎，而且對于培育學生嚴謹的思維能力，務實嚴謹的科學態度都具有重要意義，對大學生可持續發展能力的培養有著其他學科無法比擬的重要作用.那么大學基礎數學學習的好壞，對其后續專業課程的學習有多大程度的影響？大學數學課程與專業課之間有著怎樣的關系呢？

本文擬從大學數學教學改革為切入點，在江漢大學文理學院新生財管專業組織實驗班，本著同學們志愿報名原則，在實驗班增加基礎數學（包括高等數學，概率論與數理統計，線性代數）課時，優化教學內容，改革教學方法，兩年后抽取16級財管實驗班和16級財管普通班的成績，在對兩個班大學數學成績和專業課成績的統計分析基礎上，也對大學數學基礎課與專業課的相關性進行了研究和分析.

2 描述性統計分析

針對成績的基本描述，我們選取了最小值（Min），最大值（Max），中位數（Median），均值（Mean），標準差（Sd）這五個基礎統計量，其中最小最大值以及標準差可以讓我們大致了解數據的波動范圍和波動程度，而均值和中位數則分別從數值上的平均和順序上的中間兩個角度來描述數據的中間水平.

根據表1，從均值和中位數來看，二者相差不大，說明整個班的課程中成績基本集中在中間水平，極端成績很少.而所有課程的平均分均在60分及格線以上，整體成績良好.但數學類課程的中間水平在60左右，而核心類課程的中間水平要相對高一些，大部分處于60～80，說明數學能力相對薄弱;從最小最大值和標準差來看，數學類課程的最低分最高分都相對較低，也能在一定程度上說明其數學能力相比其他課程明顯弱勢.課程的標準差都集中在10左右，除了會計模擬實訓這門課，標準差最小，說明在這門課上學生成績差異最小;線性代數、管理學和經濟學基礎的標準差較大，表明學生之間的差距較大，成績分布更加寬泛.

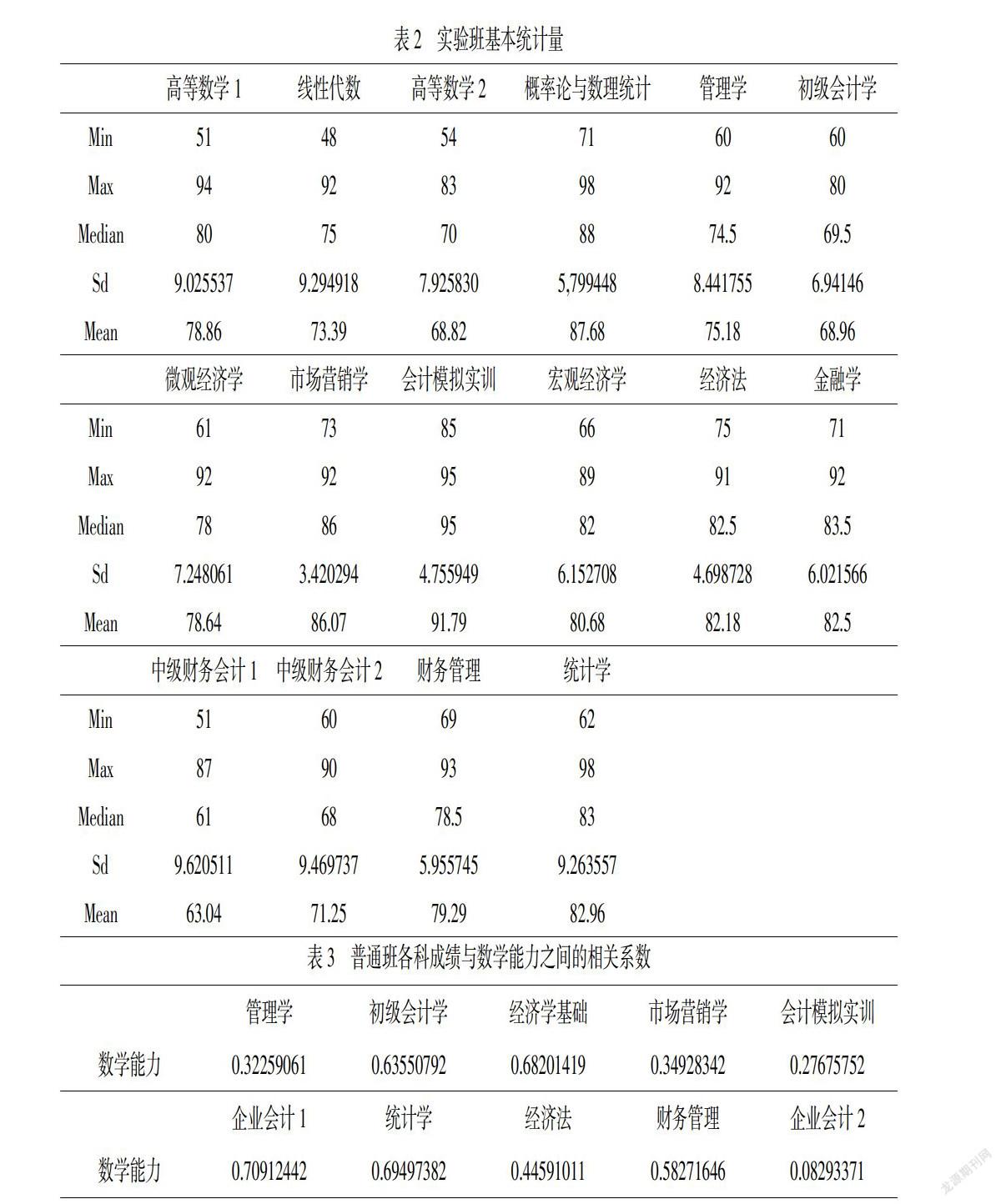
針對實驗班的16門課程進行描述性統計，根據表2，從均值和中位數來看，二者差距也很小，所以極端成績很少.所有課程的平均分均在60分及格線以上，14門課程平均分在70以上，7門課程平均分在80分以上，整體成績相比普通班更為優秀.尤其實驗數學類課程的中間水平大致在70～80，明顯成績方面更加優異，雖然數學類課程更多，但數據表現依然穩定，說明總體來看數學能力要遠優于普通班;從最小最大值和標準差來看，對比普通班，實驗班成績分布更窄，最低分最高分相對較大，各門課程的標準差均小于10，更加說明相比于普通班，實驗班課程成績波動程度較小，成績更加穩定，各個學生之間的成績差異并不是很大.

3 相關性分析

通過上述計算統計量的結果以及直方圖顯示出來的數據分布情況，我們有理由懷疑數學能力對兩個班專業課成績存在一定的影響.因此，探究專業課與數學能力之間存在的相關性，求出相關性矩陣很有必要.

從表3可以看出，在普通班上，數學能力與各科成績相關系數均為正數，除了企業會計學2這門課相關系數較低，其他科目與數學均存在明顯的正相關性，說明數學能力強的各科成績相對就高.其中數學能力與財務管理、企業會計學、統計學、初級會計學、經濟學基礎和市場營銷學的相關系數全都大于0.4，而在管理學，會計模擬實訓，經濟法這些傳統的偏文科類學科上相關系數較小，可見數學能力對專業成績的影響力較大尤其是對理學類學科.

從表4可以看出，在實驗班上，除會計模擬實訓外，數學能力與其他各科成績的相關系數均為正數，說明數學能力強的各科成績相對就高.而與會計模擬實訓課的相關系數雖為負數，但非常接近0，說明數學能力與這門課相關性不大，這與我們在普通班的相關性分析結果是一致的.對比普通班發現，實驗班的相關系數整體來說更大一些，相關性更強一些，數學與中級財務會計2、微觀經濟學、初級會計學、金融學和經濟法的相關系數都大于0.45，剩余科目與數學的相關系數也都在0.2～0.4，這些都說明數學能力對專業課程成績有明顯的正向影響.

4 數學成績與專業課綜合成績多元線性回歸

為了直觀刻畫數學能力對綜合專業成績的影響，接下來以每個班的數學類課程的學分進行加權計算出一個成績來代表其數學能力，以每個班的專業類課程按照學分進行加權算出一個成績作為專業素養成績，將得到的數據在圖1中展示出來.

從圖1中大致可以看出數學能力越強，綜合專業素養相對越高，二者之間存在一定的線性關系，因此建立簡單線性回歸分析模型.

回歸方程結果如下：

此次回歸結果系數均通過t檢驗，非常顯著，但是我們發現從常數項來看實驗班更低，可以說其基礎成績更低，但數學能力對其綜合成績影響更大，平均來看，數學能力每增加一分，實驗班綜合成績提升將比普通班成績提升多0.03分，而實驗班數學能力整體強于普通班，所以最后呈現出來的結果就是在綜合成績上實驗班強于實驗班.結果表明無論對于普通班還是實驗班，數學能力對綜合成績都有顯著正向影響.但是從我們的回歸圖可以看出兩個班的回歸線差異不大，在尾部基本重合，所以接下來我們將利用Chow檢驗來說明他們影響系數之間的差異是否顯著.原理如下：

H0：線性回歸系數無差異？圮H1：線性回歸系數有差異

計算檢驗統計量：

RSS是兩個班數據建立線性回歸的殘差平方和，RSS1是普通班建立線性回歸的殘差平方和，RSS2是實驗班建立線性回歸的殘差平方和.n1和n2分別是每個班的數據量，k是參數的總數.

在原假設情況下，統計量服從F分布.我們的數據進行鄒檢驗得到的P值為0.2952849，因此我們只能接受原假設，即在兩個班數學能力對綜合專業成績的影響沒有統計上的差異.因此為了擴大樣本量，降低統計誤差，將兩個班數據綜合考慮建立線性回歸模型如下：

y專業成績=40.97+0.48x數學

此時建立的模型截距項和回歸系數均通過t檢驗，非常顯著，且決定系數R2為0.6205，這說明專業課成績的62.05%可由數學能力來解釋，這更加說明了在大學學習中，數學對專業課學習的重大意義.因此，從數據分析來看，數學成績每提高一分，綜合專業成績提高0.48分，所以在大學數學類課程對我們專業課的培養有著重大意義.

5 結語

針對當前部分高校在“應用教育”的標簽下，出現弱化甚至取消大學數學的傾向，我校進行教改，招募志愿者組織實驗班，增加數學課程課時，優化教學內容，改革教學方法，通過實驗班和普通班比較，用實驗證實了，具備較豐富的數學知識和較好的數學素養是專業學習和可持續發展的重要途徑，并為其它課程教學改革提供新思路.

此實驗結果為學校相應專業的教學改革提出了一個新的方向——強化數學教育，使學生在大學階段學習更多的終身受用的知識，具有可持續發展的能力.且實驗結果可為同類院校教學改革提供借鑒.

——————————

參考文獻：

〔1〕李明明.素質教育視閾下大學生可持續發展能力研究[J].佳木斯大學社會科學學報，2012（12）：78-79.

〔2〕高慧璇.應用多元統計分析[M].北京：北京大學出版社，2011.

〔3〕汪消銀，周保平.數學建模與數學實驗[M].北京：科學出版社，2015.

〔4〕盛驟，等.概率論與數理統計[M].北京：高等教育出版社，2008.2.

〔5〕張紹閣.高等數學教學與專業課程結合的探索與實踐[J].教學研究，2012（4）：128-130.