新型電動閥門的速度曲線算法研究

湯偉 張越 王博 易兆祥 馬強

摘要： 中高速衛生紙機的上漿流量大，對紙漿濃度的調節精度要求高，普通的電動調節閥門難以勝任，因此，本課題組開發了一種基于直流無刷電機驅動的新型電動閥門。研究了梯形、S形速度曲線的運動規律，得出了能滿足定位精度要求的五段S形速度曲線，并在控制器中內置速度控制算法。實例驗證表明，該算法能夠將電動閥門的最小操作步長由0.9°縮短至0.069°，操作步數由100步提升到1300步。現場應用表明，該算法能夠將電動閥門的濃度調節誤差由6.32%降低至2.89%，實現了更精細的流量調節。

關鍵詞：電動閥門;速度曲線;最小操作步長;定位精度

中圖分類號：TS736+.3? 文獻標識碼：A

DOI：10.11980/j.issn.0254-508X.2019.09.007

Abstract： The domestic valve was limited to meet the high accuracy requirements of pulp consistency adjustment for medium and high speed tissue machine. New electric valve based on DC brushless motor was developed. This paper studied the movement process of triangle velocity curve and trapezoidal velocity curve. A five-stage S-shaped velocity curve which could satisfy positioning accuracy was obtained for the valve， and the velocity control algorithm was presetted in controller. The results showed that the algorithm could optimize the minimum angular displacement from 0.9° to 0.069°， and increase the operational steps from 100 to 1300. Besides， the algorithm could reduce the consistency adjustment error from 6.32% to 2.89%. The work realized the precision positioning control of electric valve.

Key words： electric valve; speed curve; minimum angular displacement; positioning accuracy

在抄紙工藝中，一般采用國產ZJKV型電動閥門對紙漿濃度進行調節，通過改變閥門的開度來改變白水的加入量，達到調節紙漿濃度的目的[1]。經實驗測定，對于0～90°角行程的ZJKV型電動閥，執行精度為100個操作步長，閥門的最小動作角度為0.9°，且閥門開度與通電時間不能夠呈現較好的線性關系，導致閥門定位精度下降;國產DN125的閥門單臺售價約為3000元[2]。BTG公司的VBW系列閥門、Metso公司的NelesACE系列閥門具有5000/10000步以上的高精度[3]，完全可以滿足濃度控制的要求，但因其價格十分昂貴，如進口DN125的閥門單臺售價在15萬～18萬元，若用于濃度調節成本過高，一般作定量調節閥使用。根據現場調研，中高速衛生紙機的濃度調節需要500～1000步之間的中高精度閥門，然而市場上還沒有技術指標合適的中間產品，諸多造紙企業對電動閥的選擇徘徊于上述兩種產品之間。隨著中高速衛生紙機的車速不斷提升，對上漿濃度提出了更高的要求，當濃度控制不穩定時，會嚴重影響成紙的一等品率[4]。因此，怎樣提高電動閥門的執行精度成為了一項重要的研究課題。

ZJKV型電動閥門與高精度閥門的差距表現在最小操作步長上，縮短最小操作步長便能夠實現轉角細分，進而精調稀白水流量，達到穩定上漿濃度的目的。電動閥門的轉角時間特性反映其定位精度，一般采用速度曲線來描述閥芯的轉角運動規律。驅動電機在一定程度上影響著電動閥門的定位效果，普通電動閥由三相異步電機驅動，而異步電機本身的定位精度不高，因此，具有較高定位精度的直流無刷電機被用于驅動閥門，并采用合適的速度曲線算法使電動閥門達到更精確的定位效果，來滿足中高速衛生紙機的濃度調節要求。

本課題組開發了一種基于直流無刷電機驅動的新型電動閥門，研究了梯形、S形速度曲線的運動規律，以得到滿足定位精度要求的五段S形速度曲線，并在控制器中內置速度控制算法。

1 電動閥門的結構改進

1.1 普通電動閥門的結構

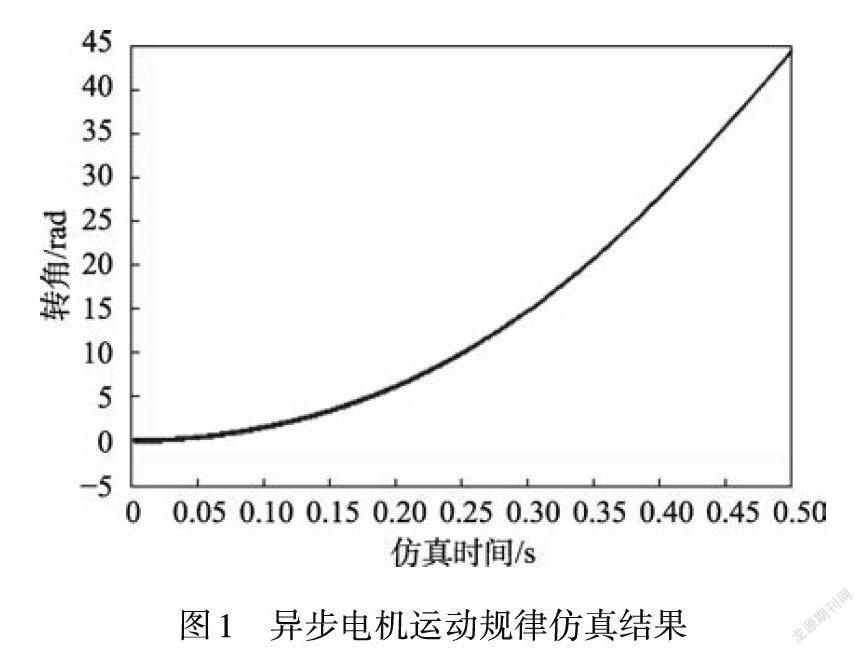
ZJKV型電動閥門由異步電機驅動，電機的輸出軸連接圓柱齒輪減速器，圓柱齒輪末端的中心與蝸桿剛性固接在一起，成為同軸，電機轉軸經圓柱齒輪減速、蝸輪蝸桿增矩后，將動力傳輸至閥桿，最終由閥桿帶動V型球閥完成轉動。筆者在MATLAB中搭建仿真模型，探究異步電機的轉子運動規律，結果如圖1所示。

由圖1可知，異步電機的轉角與時間呈非線性關系，當電機驅動閥桿轉動時，閥芯所獲得的轉速值遠離規定轉速[5]。另外，由于缺少有效的閥位反饋信號，閥芯在轉動的過程中處于不受控狀態。因此，異步電機本身不適合用于電動閥門的精密定位控制。

1.2 改進型電動閥門的結構

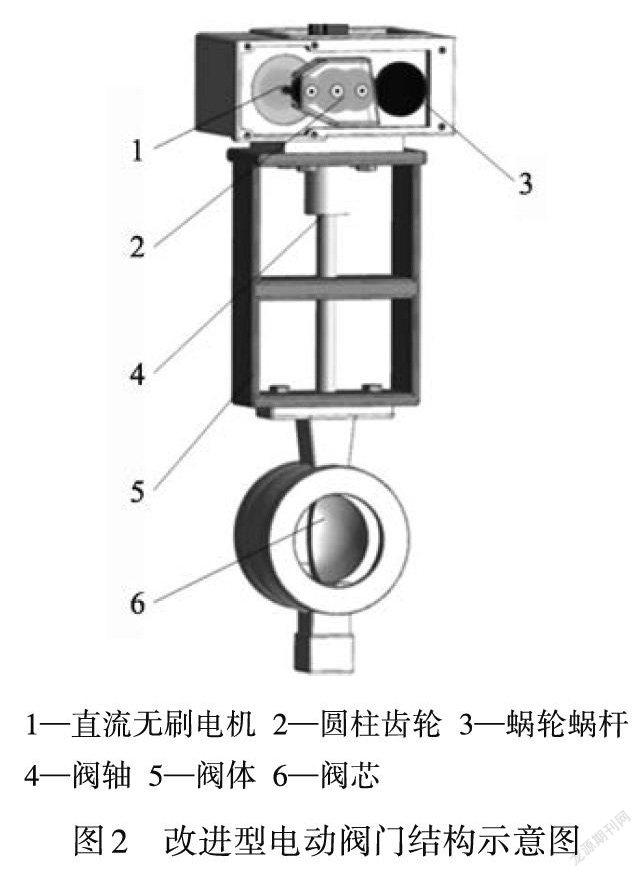
直流無刷電機的轉矩與轉速之間為線性比例關系，在電機驅動板中具有無級調節轉速的選擇功能項[6-7]。為確保閥芯在動作過程中的轉速具有可控性，筆者采用直流無刷電機作為電動閥門的驅動部件，保持原來的傳動系統，僅將異步電機更換為直流無刷電機，改進型電動閥門的結構如圖2所示。在結構改進的基礎上，用型號為LY-F2的單片機開發板和直流電機驅動器作為電動閥門的驅動控制單元，其新增成本約280元。電動閥門由直流電機驅動器提供直流24 V的供電電源，LY-F2可接收4～20 mA的閥位反饋信號、數字量的開關閥反饋信號以及全開或全關反饋信號，通過輸出開關閥控制信號和PWM調速信號實現電動閥門的定位控制。

1.3 速度曲線與閥門定位精度的關系

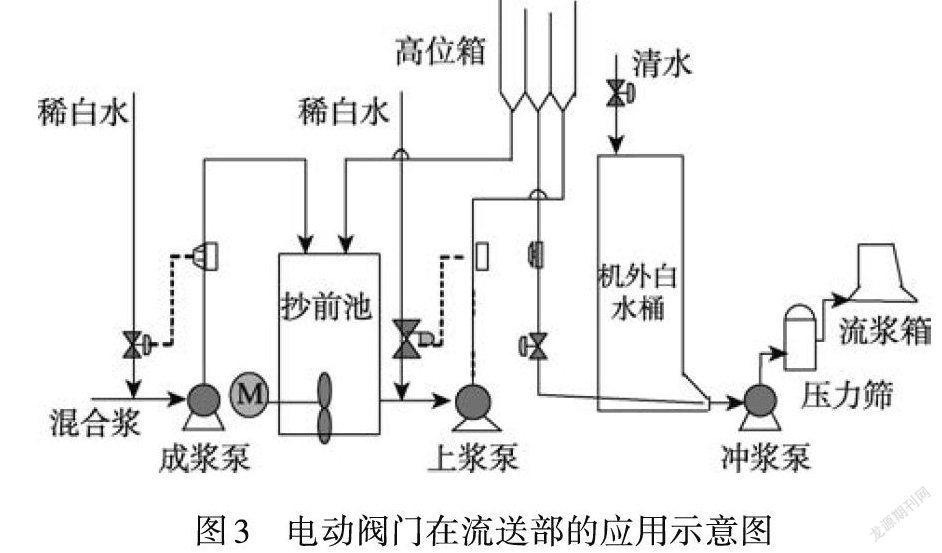
在中高速衛生紙機的流送部，紙漿經歷2個濃度調節過程以達上漿要求，其工藝流程如圖3所示。

由圖3可知，混合漿在進入成漿泵之前，首先要經過一次調濃，然后進入抄前池，再經過二次調濃后由上漿泵送入高位箱中靜置，隨后進入白水塔稀釋，最后由沖漿泵送入流漿箱。在紙漿濃度的閉環控制回路中，電動閥門屬于執行器，其開度大小決定著稀白水的流量，進而影響著紙漿濃度。當濃度計檢測到紙漿濃度高于設定值時，控制器輸出數字量信號將電動閥門開度變大，通過增加稀白水的通入流量使得紙漿濃度穩定，反之亦然[8-12]。在紙機流送部的濃度調節過程中，閥芯必定會經歷由靜止加速到規定轉速和由規定速度減速至靜止，若加減速預置定位曲線設計不合理，易導致閥芯不能準確抵達預設位置，導致紙漿的濃度紊亂[13]。因此，合理的速度預置曲線能夠有效地提升電動閥門的定位精度。筆者以電機的轉子輸出軸為研究對象，對比研究3種速度預置算法在電動閥中應用的優缺點。

2 電動閥門的定位曲線研究

2.1 梯形速度曲線

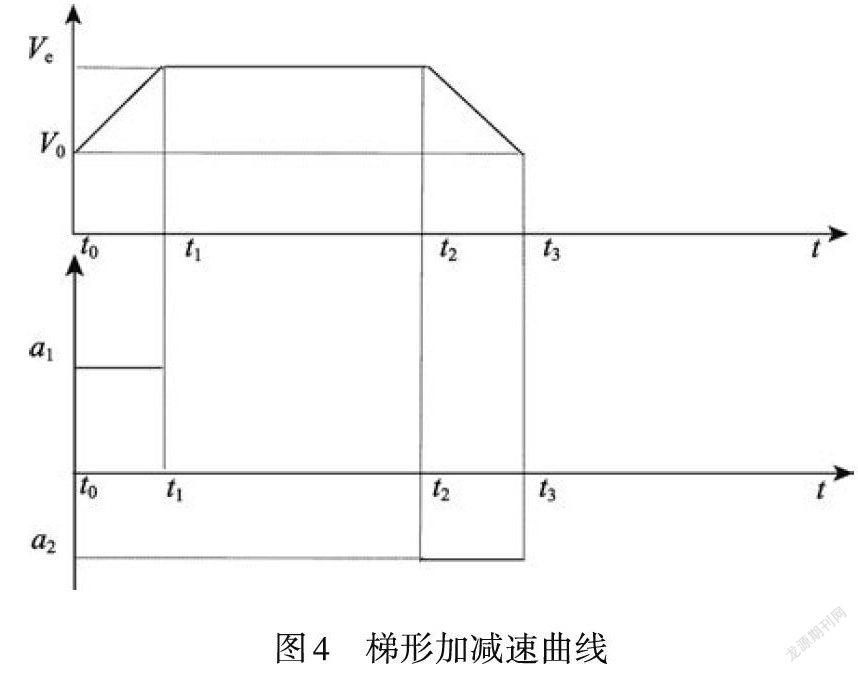
梯形加減速曲線包含勻加速、勻速和勻減速段，其運動規律如圖4所示。從圖4可看出，在梯形加減速定位曲線中，t0～t1是加速度為a1、初速度為V0的加速過程，t1～t2是速度為Ve的勻速過程，t2～t3是以加速度為a2的減速過程，可見，加速度存在突變現象，容易引起轉子抖動，進而造成閥芯定位不準確[14]。為避免電動閥門發生過沖或丟步等現象，需使驅動電機的輸出力矩連續。因此，對加速度連續的速度預置算法的研究顯得十分必要。

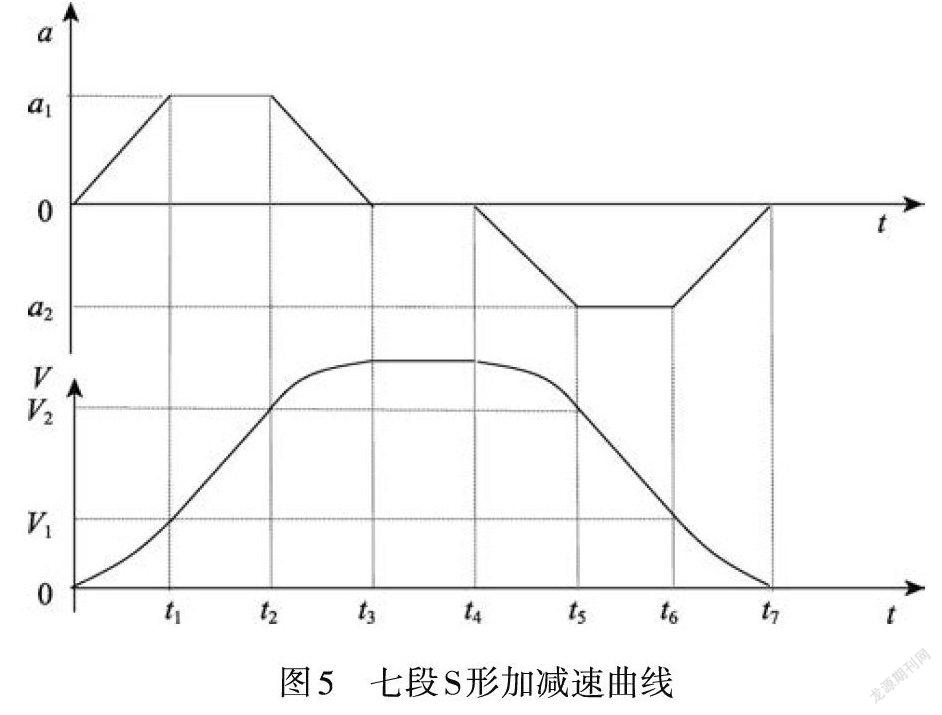
2.2 七段S形速度曲線

七段S形速度曲線具有加速度連續的特點，所描述的運動規律如圖5所示[15-16]。由圖5可知，在七段定位過程中，加速過程與減速過程完全相逆，加速過程的特征函數可映射到閥芯的整個運行狀態中。令每一段運動過程結束時刻的速度分別為～，角位移分別為～。第一段0～t1為加速度a按固定比率增大的勻變加速過程，其速度V、角位移S與時間t的關系可表示為式（1）。

第二段t1～t2是加速度a為恒定值a1的勻加速過程，可表示為式（2）。

第三段t2～t3為加速度a按固定比率減小的勻變加速過程，可表示為式（3）。

第四段t3～t4為轉子保持勻速Ve運行過程，可表示為式（4）。

第五段t4～t5是加速度按固定比率增大的勻變減速過程，可表示為式（5）。

第六段t5～t6是加速度為恒定值的勻減速過程，可表示為式（6）。

第七段t6～t7為加速度按固定比率減小的勻變減速過程，可表示為式（7）。

根據上述函數關系可知，七段S形速度預置算法的實現過程頗為繁瑣，涉及多組包含轉子運動特征的時間分配問題以及相關數據的處理過程，與梯形速度預置算法相比，該速度預置算法使得控制器的運算時間延長，一旦輸出信號的耗時比程序的運行周期短，就會導致電動閥門停轉[17-19]。因此，需要對傳統七段S形速度預置算法進行改進研究。

2.3 五段S形速度曲線

在七段S形加減速曲線的基礎上去掉兩段加減速過程，得出了五段S形加減速定位曲線，其描述的運動規律如圖6所示。令各加、減速階段的耗用時間均為tm，勻速階段的耗時為tave，令每一段運動過程結束時刻的速度分別為～，角位移分別為～。第一段加速過程為加速度a以固定比率增加的勻變加速過程，經過第一個加速過程后速度達到V1，然后進入加速度a以固定比率減小的勻變加速過程，經第二個加速過程后達到規定轉速Ve并勻速運行時長tave，最后進入與加速過程相逆的減速階段，其中，加速度的最大值用am表示，且存在V2=V3=Ve。第一段0～tm加速過程的運動狀態特征為式（8）。

第二段tm～2tm加速過程的運動狀態特征為式（9）。

第三段2tm～（2）勻速過程的運動狀態特征為式（10）。

第一段與第五段、第二段與第四段所描述的速度變化規律相逆，故可將減速環節看作加速環節的逆過程，電動閥經歷減速階段所獲得的角位移等于加速階段所對應的角位移，且在減速環節的末尾時刻閥芯的轉速降為零。關于減速階段的運動特征函數關系，此處不再贅述。假設轉子以速度轉動，在五段S形加減速曲線中，添加一段加速度為0、在規定轉速工況下的速度曲線，構成轉子在理想與實際兩種情況下的運動規律對比示意圖，如圖7所示。

由圖7可知，粗線代表轉子在理想情況下的運動規律，令0～tm、tm～2tm、2tm～（2tm+tave）每個時間段結束時刻所對應的理論角位移分別為、和，實際角位移分別為S1、S2和S3，將理論曲線與五段S形加減速曲線進行對比分析后，可得到經驗公式如式（11）所示。

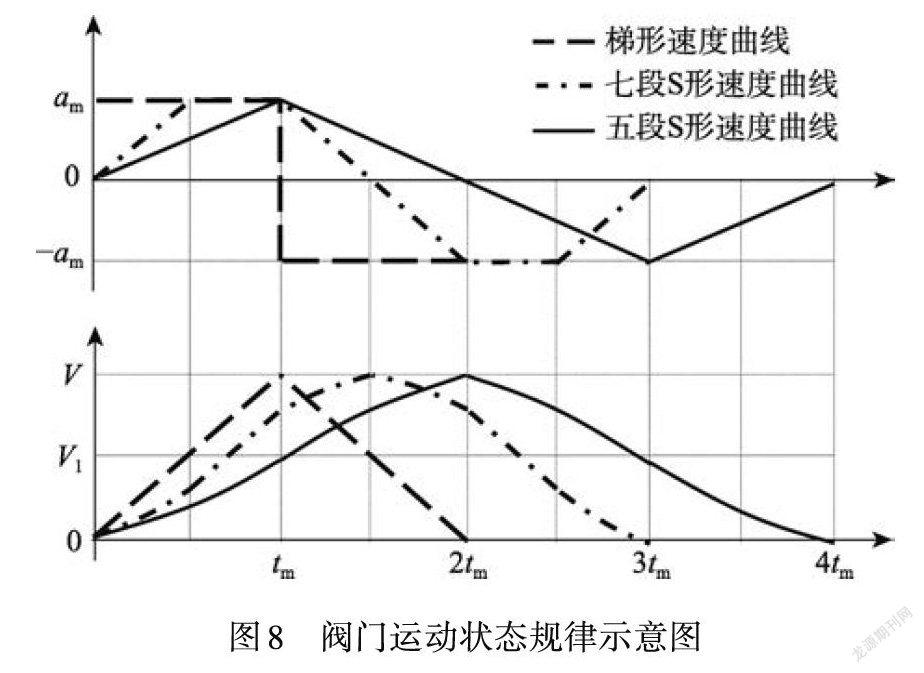
根據式（11）可知，閥芯經歷第一段加速過程后所獲得的角位移與理論角位移之間的差量剛好由第二段加速過程來彌補，閥芯經歷減速過程所獲得的實際角位移等于第二段加速過程對應的理論角位移，閥芯最終獲得的角位移恰好等于理論值。因此，在五段S形速度預置算法中，減速階段可視為描述電動閥門在實際應用中轉角缺陷的補償過程。圖8說明了電動閥門在3種速度曲線下的運行規律。

由圖8可知，tm=Ve /am，梯形速度曲線的加速時間為改進型速度曲線的1/2，為傳統七段S形速度曲線的2/3，說明閥芯在梯形速度曲線下能夠最快達到規定轉速Ve，由于其加速度的變化率在瞬間趨近于無窮大，不符合實際情況，該種狀態特征不能為電動閥的應用提供依據。與七段S形速度預置算法相比，改進型速度曲線的加速過程耗時雖然最長，但是該算法的設計過程較為簡單，表現在其兩段加速過程對應的角位移之和等效于相同時間內理論角位移的1/2，減速過程亦然。因此，改進型速度預置算法能夠有效降低設計的復雜性，容易求得閥芯在實際使用過程中的角位移特征。

3 速度曲線算法的工程實現

3.1 算法設計流程

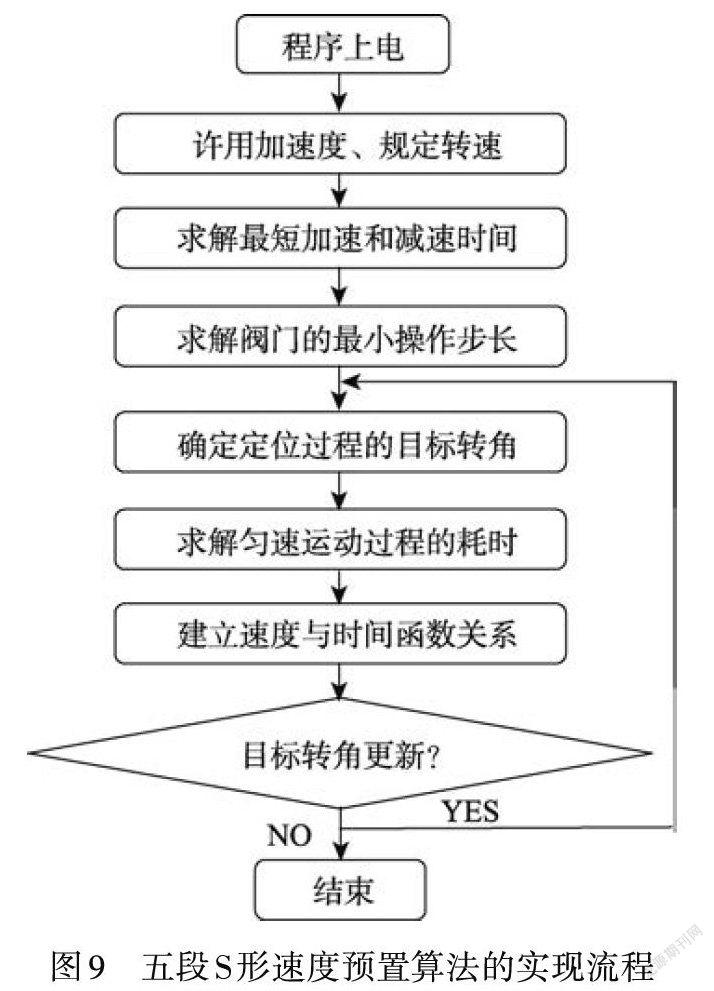
在LY-F2中采用ATMega328P芯片來實現五段S形速度預置算法作為電動閥門定位控制的設定值，在Arduino IDE的集成編譯環境中進行程序設計，該算法的實現流程如圖9所示。根據許用加速度和最短加減速時間，能夠設計出描述五段S形速度曲線的加速段函數和減速段函數，根據定位過程的目標轉角，可以確定勻速段函數，其中，最小操作步長可以用來判定電動閥門的定位精度。

3.2 驅動控制參數

設計電動閥門的負載轉矩為110 Nm，驅動電機的額定轉矩為0.095 Nm，轉子軸與閥桿之間的減速比為1500∶1，折算至轉子軸的應受負載轉矩為0.073 Nm，為保留一定裕量，將該值放大18%，得到電機的額定負載轉矩為0.086 Nm。以轉子輸出軸為研究對象，不計阻尼轉矩，加速度和驅動轉矩之間的關系可表示為式（12）。

Te =TL+（12）

式中，Te為驅動轉矩，TL為負載轉矩，J為轉動慣量。

經查閱手冊，取J = 3.65 kg·cm2，求得 rad/s2，為保護驅動電機，取許用加速度，作為電動閥運行的最大加速度。在使用過程中，電動閥不必受限于驅動電機的額定轉速，可根據閥芯的執行時間來配置規定轉速，使電動閥門具有一定的柔性調節功能。所設計電動閥門的執行時間范圍是100～400 s，對應的閥芯轉角都是0.785 rad，即閥芯最快能夠在100 s內按照速度預置曲線由全開到全關，最慢能夠在400 s內按照速度預置曲線由全開到全關。

電動閥門的執行時間與規定轉速之間的函數關系見式（13）。

式中，為規定轉速，為減速比，m表示執行時間。可求得當閥芯的執行時間為400 s時，驅動電機的規定速度為2.94 rad/s，當閥芯的執行時間為100 s時，驅動電機的規定速度為11.77 rad/s。

3.3 閥門最小操作步長

在某個確定的執行時間狀態下，縮短加減速過程的耗用時間能夠轉角細分，在3種定位算法下，得到描述電動閥加速階段的時間分配方式如表1所示。

以執行時間為400 s的電動閥門為例，五段S形速度預置曲線的加速段函數表達式為式（14）。

勻速階段的函數關系不予考慮，令減速階段的初始狀態為零時刻，其函數表達式為式（15）。

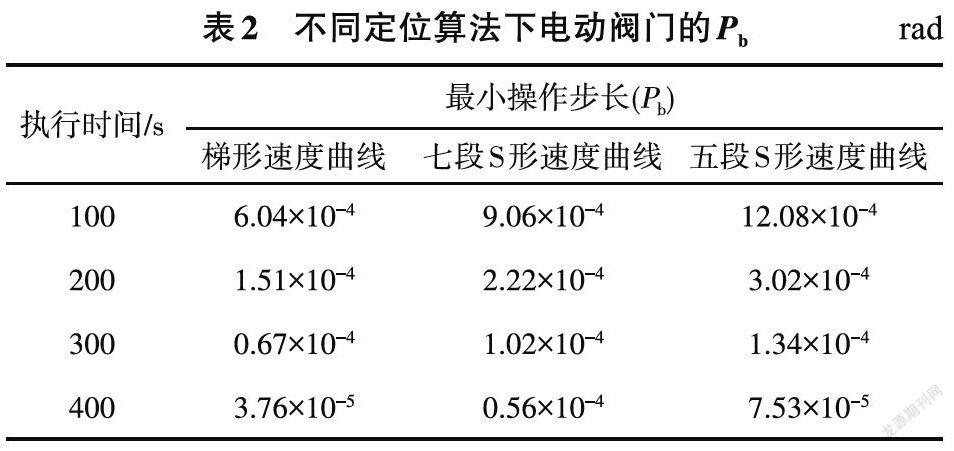
經歷加速過程后立即進入減速過程，產生的角位移對應的最小操作步長，用Pb表示，總有Pb=kVet/i，其中，代表轉角比例系數。為研究電動閥門在3種定位算法下的轉角細分情況，求得在不同執行時間下的Pb，結果如表2所示。

上述研究結果表明：

（1）在五段S形速度預置算法下，當電動閥門的執行時間為400 s時，每段加速過程的耗用時間不得低于38.46 ms，當執行時間為100 s時，每段加速過程的耗用時間不得低于152 ms，否則容易導致轉子的輸出力矩不足，引起閥芯產生抖動現象。

（2）五段S形速度預置算法的Pb為梯形速度曲線的2倍，為七段S形速度曲線的1.33倍，延長執行時間能夠進一步減小Pb。

（3）對于執行時間為100 s的電動閥門，改進型速度預置算法能夠將Pb由原來的0.9°縮短至0.069°，操作步數可由100步提升到1300步。

4 新型電動閥門的應用效果

將開發的新型電動閥門試用于保定某紙廠的8#高速衛生紙機，負責流送部的紙漿濃度調節過程，將濃度變化情況作為一項評價電動閥門定位精度的指標，現場應用如圖10所示。

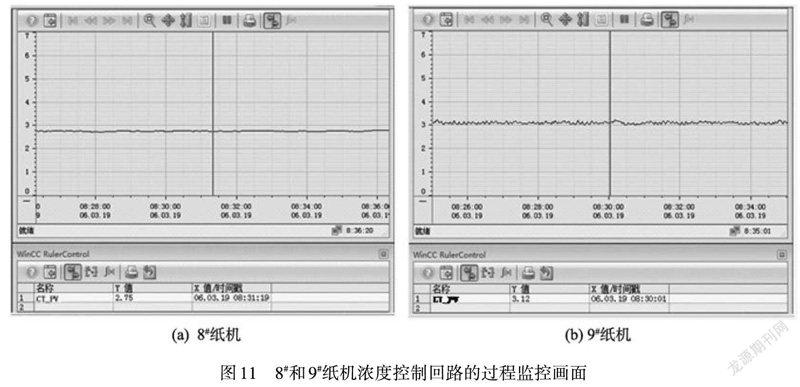
在圖10中，稀釋白水自上而下流經電動閥門，閥門的開度影響著白水的流量值，進而決定紙漿的濃度大小，可以通過濃度計現場讀取濃度值，也可以在Wincc V7.3軟件中實時監控濃度的波動情況。為對比更換電動閥門前后紙漿濃度的調節質量，截取同一時間段內8#紙機與9#紙機的濃度監控畫面，如圖11所示。

圖11（a）中8#紙機采用改進型電動閥門進行調節，紙漿濃度的設定值為2.77%，當前時刻濃度的過程值為2.75%;圖11（b）中9#紙機仍然采用原來的電動閥門進行調節，紙漿濃度的設定值為3.07%，當前時刻濃度的過程值為3.12%。與原來普通電動閥門的工作狀態相比，8#紙機的濃度過程值更加趨于穩定狀態，不存在明顯的波峰和波谷，而9#紙機的濃度過程值具有明顯的波動現象，最大值為3.22%，最小值為2.98%。在600 的測試時間內，新的濃度調節過程減少了58個波峰、49個波谷，濃度調節的誤差率可由原來的6.32%降低至2.89%，說明基于五段S形速度預置算法的電動閥門可以表現出更優的定位特性，能夠使得紙漿濃度的過程值嚴格維持在設定值上。

5 結 論

ZJKV型電動閥門是在紙機流送部中負責白水調濃的重要執行器，其定位精度直接決定著成紙質量。分析了造成閥門定位精度不足的原因，以成本增加不多為改進原則，換用直流無刷電機驅動執行機構，提出將五段S形速度預置算法用于電動閥門的定位過程中，并設計了當執行時間為400 s的速度函數。研究表明，改進的五段S形速度預置算法可將Pb由原來的0.9°縮短至0.069°，把電動閥門的操作步數由100步提升到1300步，使濃度調節過程的誤差由原來的6.32%降低至2.89%，有效地提高了電動閥門的定位精度，能夠滿足中高速衛生紙機對上漿濃度的嚴格要求。

參 考 文 獻

[1] TANG Wei， PANG Xiao， WANG Qi， et al. A Control Scheme for Stock Approach System of Domestic High Speed Tissue Machines[J]. China Pulp & Paper， 2015， 34（8）： 49.

湯 偉， 龐 肖， 王 琦， 等. 一種國產高速衛生紙機流送系統控制方案[J]. 中國造紙， 2015， 34（8）： 49.

[2] Liu Jiayi. Intelligent Status and Development Trend of Electric Valves[J]. China Petroleum and Chemical Standard and Quality， 2018， 38（10）： 90.

劉嘉益. 電動閥門的智能化現狀及其發展趨勢[J]. 中國石油和化工標準與質量， 2018， 38（10）： 90.

[3] Metso Automation Neles Valve Company. Neles Ace Basis Weight Control Unit Installation， Maintenance and Operating Instrument [R]. Helsinki， Finland， 2016.

[4] YANG Xu， ZHANG Hui. Prospects for the 13th Five-Year Plan for China's Pulp and Paper Equipment Manufacturing Industry[J]. China Pulp & Paper， 2016， 37（11）： 32.

楊 旭， 張 輝. 我國制漿造紙裝備制造業“十三五”發展展望[J]. 中國造紙， 2016， 37（11）： 32.

[5] Zou Yuanwei， Wan Heng. Simulation of Torque Stability Optimization Control for Asynchronous Motor[J]. Computer Simulation， 2017， 34（12）： 292.

鄒元威， 萬 衡. 異步電機轉矩穩定性優化控制設計仿真[J]. 計算機仿真， 2017， 34（12）： 292.

[6] Baek S W. Optimum shape design of a BLDC motor for electric continuous variable valve timing system considering efficiency and torque characteristics[J]. Microsystem Technologies， 2018， 24（11）： 4441.

[7] Zhang Qingchao， Ma Ruiqing， Zhang Zhen， et al. Electromagnetic Torque Obeservation of Brushless DC Motor Based on Hall Position Signals[J]. Transactions of China Electrotechnical Society， 2015， 30（10）： 187.

張慶超， 馬瑞卿， 張 震， 等. 基于霍爾位置信號的無刷直流電機電磁轉矩觀測[J]. 電工技術學報， 2015， 30（10）： 187.

[8] TANG Wei， HUANG Baozhu， HU Xiangman， et al. Improvement of High-precision Quantitative Valve Controller Based on S7-200[J]. China Pulp & Paper， 2016， 35（12）： 43.

湯 偉， 黃寶柱， 胡祥滿， 等. 基于S7-200高精度定量閥控制器的改進研究[J]. 中國造紙， 2016， 35（12）： 43.

[9] Wang Bo. Study on Precision Position Strategies for Paper Basis Weight Control Electric Valve Actuators[D]. Xian： Shaanxi University of Science & Technology， 2018.

王 博. 紙張定量控制電動閥門執行器精密定位策略研究[D]. 西安： 陜西科技大學， 2018.

[10] Zhao Huixian， Wu Xinwei. Control System Design and Application of Electic Actuators[J]. Instrument Technique and Sensor， 2017（4）： 83.

趙慧嫻， 吳新偉. 一種電動執行器控制系統設計與應用[J]. 儀表技術與傳感器， 2017（4）： 83.

[11] Wang Bo， Tang Wei， Dong Jixian， et al. Research and Development of Domestic Dilution Water Headbox’s Dilution Valve Controller[J]. Fluid Machinery， 2015， 43（4）： 48.

王 博， 湯 偉， 董繼先， 等. 國產稀釋水閥控制器設計[J]. 流體機械， 2015， 43（4）： 48.

[12] WANG Bo， TANG Wei， DONG Jixian， et al. Design of Cross Direction Basis Weight Control Actuator of Dilution Water Hydraulic Headbox[J]. China Pulp & Paper， 2015， 34（5）： 41.

王 博， 湯 偉， 董繼先， 等. 稀釋水水力式流漿箱橫幅定量控制執行器設計[J]. 中國造紙， 2015， 34（5）： 41.

[13] Wang Bangji， Liu Qingxiang， Zhou Lei， et al. Design of Stepper Motor Velcity Profile and Realization on FPGA[J]. Micromotors， 2012， 45（8）： 67.

王邦繼， 劉慶想， 周 磊， 等. 步進電機速度曲線的設計與FPGA實現[J]. 微電機， 2012， 45（8）： 67.

[14] WANG Bo， TANG Wei， LIU Qingli， et al. Research and Development of Medium High-precision Quantitative Valve for Basis Weight Control of Paper Machine[J]. China Pulp & Paper， 2014， 33（3）： 39.

王 博， 湯 偉， 劉慶立， 等. 國產造紙機用中高精度定量閥的研制[J]. 中國造紙， 2014， 33（3）： 39.

[15] Wang Bo， Tang Wei， Dong JiXian， et al. Positioning-control Based on Trapezoidal Velocity Curve for High-precision Basis Weight Control Valve[J]. Paper and Biomaterials， 2017， 2（2）： 42.

[16] Yuan Jipeng， Huang Zuguang， Zhang Chengrui， et al. Selection Strategy of Freedrate Planning Algorithm for Robot Point to Point Contrl[J]. Manufacturing Technology & Machine Tool， 2018（12）： 143.

袁佶鵬， 黃祖廣， 張承瑞， 等. 機器人點位控制速度規劃算法選擇策略[J]. 制造技術與機床， 2018（12）： 143.

[17] He Jie， Wang Zhengrong， Mark King， et al. Research on prediction methods for motor vehicle driver training demand based on an S-curve[J]. Transportation Research Part F： Psychology and Behaviour， 2018， 58（7）. 834

[18] Fang Jiawei， Cai Jinda， Yao Ying， et al. S-type Acceleration and Deceleration Control Method Based on Sigmoid-function[J]. Journal of Mechanical & Electrical Engineering， 2018， 35（9）： 933.

方佳偉， 蔡錦達， 姚 瑩， 等. 基于Sigmoid函數的S型加減速控制方法研究[J]. 機電工程， 2018， 35（9）： 933.

[19] Zhang Zhisong. Trajectory Planning of Palletizing Robot Based on Double S-shaped Velocity Curve[J]. Mechanical & Electrical Engineering， 2018， 35（3）： 330.

張志松. 基于雙S形速度曲線的混聯碼垛機器人軌跡規劃[J]. 機電工程， 2018， 35（3）： 330.

（責任編輯：常 青）