三位一體實施“沖激信號定義”教學

李文娟 周杰 李傲梅

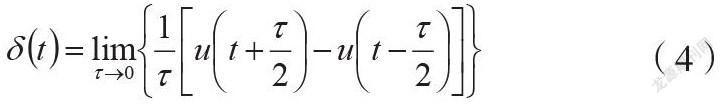
摘要：針對“信號與系統”課程中沖激信號的定義復雜難懂的特點，從工科學生的認知特點出發，通過物理現象、工程近似模型和嚴格數學定義三個維度由淺入深地分析沖激信號的三位一體特性，達到將抽象的定義具體化、系統化、實用化的目的。教學反饋表明，該方法有利于啟發學生從形象思維到抽象思維的轉變，使學生能夠更加深入地理解所學知識，教學效果良好。

關鍵詞：沖激信號;信號極限;狄拉克函數;廣義函數

信號與系統課程是通信、信息相關專業的學科基礎課程。在該課程中，沖激信號的作用至關重要，它既可以用來分解任意一個信號，又可以通過它的零狀態響應做傅里葉變換或拉普拉斯變換得到系統的頻率特性或系統函數[1]。但是，在沖激信號知識點的教學過程中，學生普遍反映定義較抽象難懂，對不同定義方式之間的關系把握不清，從而導致對性質理解不透，影響了后續相關知識點的學習與掌握。

本文從沖激信號的物理現象案例引入，激發學生思考，并梳理沖激信號的不同定義之間的相互關系，分別從物理現象描述、工程近似模型分析和嚴格數學定義解釋三個角度詳細闡述沖激信號的定義，達到使學生能夠全方位地深入理解沖激信號相關知識點的目的，在教學中起到了事半功倍的作用。

1 從物理現象到狄拉克函數定義

其中，F為作用力，t為作用時間，I為沖量。對于確定的彈射現象，I為常量，由此便可得出作用時間越短、作用力越大，并且積分有限的特性。這三個特性實際上就是狄拉克函數所表示的含義，如式（2）、式（3）所示。

式（2）表示的狄拉克函數的第一個條件含義比較直觀，式（3）表示的第二個條件較難理解，教學時可在此處不去解釋，而在講解基于函數極限的沖激信號定義時再來解釋這一條件。

在狄拉克函數定義的教學中，可以穿插有關科學怪才狄拉克的歷史人文知識，使學生既能夠通過學習前人的研究精神和思維方式提升自己的科學素養，又能夠進一步理解狄拉克函數的提出背景和深刻含義。2009年，倫敦博物館資深研究員格雷厄姆.法米羅出版了一本關于狄拉克的傳記文學作品，書名中直呼這位科學天才為“最奇怪的人”。狄拉克常常具有令人費解的驚人思路的根本原因在與他是一個異乎尋常的“科學混血兒”。狄拉克身上有一部分是理論物理學家，有一部分是理論工程師，還有一部分是純粹數學家。因此，他所提出的狄拉克函數，正好就是這種三位一體的科學技術理論的完美產物。這正驗證了狄拉克本人所說的話：“一個數學理論如果是真正漂亮的話，她一定會顯示為一種優雅而重要的物理現象。”狄拉克函數就是一種能夠解釋重要物理現象的數學理論，因此被譽為“最優美的函數”[2]。

2 從工程近似模型到基于函數極限的定義

沖激信號作為解決實際問題的數學模型，在現實中是不存在的，它是理想的數學模型，可以將其理解為規則函數的極限得到的數學模型[3]。這里可以繼續分析引課所用的實際案例，根據實際中的電磁彈射瞬間的沖擊波形圖說明理想與現實的差距，并指出通過化繁為簡的思想解決現實中出現的實際問題的思維模式。

在基于函數極限的沖激信號定義教學中，可以采用動畫的方式讓學生直觀地感受從規則函數到沖激信號的逼近過程。以脈沖函數的極限為例講解比較直觀，假設脈沖的寬度為，高度為，可以得到關系式如式（4）所示。

脈沖面積固定為1保持不變，縮短脈寬，脈沖高度就會相應變高，當脈寬無限小趨于零時，脈沖高度趨于無窮大，此時得到的信號就是單位沖激信號。這里的脈寬為零、脈沖高度無窮大就對應了式（2）所表示的狄拉克函數的第一個條件含義。而脈沖面積固定為1與式（3）所表示的積分為1含義相同。由此可以得出，基于狄拉克函數和基于信號極限的兩種沖激信號定義方式含義是相吻合的，都是為了表示持續時間極短、取值極大和積分有限的含義。

需要強調的是，矩形脈沖在實際中也是無法實現的，實際中的信號往往更逼近于三角脈沖、雙邊指數脈沖、鐘形脈沖、抽樣函數等等[4]。因此，根據這幾類信號的極限同樣可以得到沖激信號。這一部分可以作為知識拓展讓學生課下討論研究。

3 從嚴格數學理論到基于廣義函數的定義

在工程應用中，掌握狄拉克函數定義和基于信號極限的定義方式基本已經夠用。然而，從數學嚴密性來講，這兩種定義方式是存在數學漏洞的[5]。

例如，考察信號。顯然，沖激偶信號包含正負極性的兩個沖激信號，它不屬于沖激信號的范疇，因此自然也不是沖激信號。如果把帶入狄拉克函數的定義式，可以得到

即不是沖激信號，卻滿足狄拉克函數的定義。因此，狄拉克函數對沖激信號的定義是不嚴謹的，是存在數學漏洞的。

事實上，在狄拉克提出這種函數的時候，按照那時所形成的數學理論，是無法理解這種奇特的函數的。但正是這種看似奇特的函數，當它被參與數學運算后所得到的數學結論與物理結論確是正好吻合的。這就迫使理論學家們要為這類奇特的函數尋找嚴格的數學定義。后來，隨著廣義函數理論的發展，人們發現，對沖激信號比較嚴格的定義方式是基于廣義函數的定義。廣義函數的定義如式（6）所示。

其中，為檢驗函數，廣義函數是對檢驗空間中的每個函數賦予一個函數為N的映射。按照廣義函數理論，沖激信號可這樣定義：

因此，沖激信號屬于廣義函數的一種。

這里，可利用式（7）的沖激信號定義方式考察信號。由于

因此，根據廣義函數的定義，不滿足沖激信號的定義。正因為基于廣義函數的沖激信號定義具有嚴密的數學基礎，可以由此得出沖激信號的一系列重要性質，式（7）所示的就是沖激信號的篩選性質。另外，還可以通過沖激信號的廣義函數定義證明沖激信號的其他性質。

4 結語

沖激信號作為信號與系統課程中的一類重要的奇異信號，其應用貫穿了課程的始終。本文從實際物理現象、工程近似模型和嚴格數學理論三個角度說明了沖激信號的三位一體特性，并分別剖析了狄拉克函數定義、基于信號極限的定義和基于廣義函數的定義三種定義方式，闡述了這三種定義方式之間的區別與聯系，使學生能夠更加深入地理解沖激信號，為后續沖激信號的性質及應用的學習夯實基礎。

參考文獻：

[1]楊忠林，歐陽華，候新國，王家林. 沖激函數教學方法的初步探討[J]. 課程教育研究，2016（13）：34-37.

[2]陳關榮. 狄拉克和他的δ函數[J]. 數學文化，2016（6）：106-113.

[3]陳光紅. 《信號與系統》中沖激函數δ（t）的教學探討[J]. 電腦知識與技術，2011（25）：13-17.

[4]張盛峰，代少升，雷芳. 信號與系統中單位沖激函數教學方法研究[J]. 大眾科技，2013（11）：174-176.

[5]徐斌. 沖激函數匹配法在信號與系統教學中的應用研究[J]. 文理導航（下旬），2014（2）：29-31.

作者簡介：

1.李文娟，女，1985年2月出生，碩士，講師，研究方向為信號與信息處理;

2.周杰，男，1979年9月出生，博士，講師，研究方向為多源信息融合;

3.李傲梅，女，博士，教授，研究方向為信息與通信工程。