基于相關性準則和R-ELM模型的巖溶隧道涌水量預測研究

賀華剛

(重慶工商職業學院, 重慶 400052)

0 引言

隨著我國交通基礎建設的快速發展，隧道工程數量日益增加，受地質環境條件的影響，隧道施工過程中的工程問題日益突出，例如隧道涌水災害。隧道涌水災害不僅延誤工期，還會帶來嚴重的經濟損失，尤其在巖溶地區，該類問題更加突出。因此，開展巖溶隧道涌水災害研究具有重要意義。目前，國內許多研究者已開展了隧道涌水預測方面的研究。楊卓等[1]利用BP神經網絡構建了巖溶隧道突涌水風險評估模型，可為支護方案的選擇提供依據；王者鵬等[2]通過分析水文地質特征，構建了巖溶隧道的涌水預測模型，可合理判斷施工過程中的涌水區段；張雄文[3]利用儲量分類法分析了地下巖溶水的空間分布特征，并在此基礎上進一步研究了降雨與地下水儲量之間的對應關系。根據上述研究成果可知，巖溶區的隧道涌水災害極易發生，但研究均未涉及隧道涌水影響因素的篩選。同時，根據黃雄軍[4]、許增光等[5]的研究成果可知，隧道涌水受多種因素的共同作用，并不是單一因素的作用結果，且不同因素的影響程度具有一定差異，因此有必要進行篩選分析。本文以通海隧道為工程背景，在對隧道涌水影響因素進行分析的基礎上，利用相關系數法和極限學習機構建了隧道涌水預測模型，旨在實現隧道涌水的高精度預測，以期為現場災害防治提供參考。

1 預測模型的基本原理

隧道涌水預測模型主要包括： 涌水影響因素的篩選和預測模型的構建。在影響因素的篩選過程中，先結合文獻[6-7]的研究成果，構建了隧道涌水影響因素體系； 以現場涌水統計結果為基礎，利用相關系數法分析不同因素對隧道涌水的影響程度，進而篩選出重要影響因素。在預測模型的構建過程中，將已篩選出的重要影響因素作為輸入信息，且為保證預測精度，先利用試算法和經驗公式優化極限學習機的模型參數，再利用M估計優化誤差序列，進而構建出隧道涌水的優化預測模型，以達到高精度預測的目的。

1.1 影響因素的篩選

在以往隧道涌水影響因素分析中，多從各方面構建隧道涌水影響因素體系，但并未進一步探討各因素對隧道涌水的影響程度。為實現不同影響因素與隧道涌水災害間的相關性篩選，本文以相關系數法為理論基礎，通過相關系數評價各影響因素對隧道涌水的影響程度。相關系數法是一種統計理論方法，具有操作簡單、可信度高等優點，適用于評價相關指標間的緊密程度。在該方法的應用過程中，若評價指標為xi和yi，i=1,2,…,n，則兩者的相關系數

(1)

式中x′、y′為對應評價對象的平均值。

根據相關系數r的正負及其絕對值大小即可判斷評價指標間的相關性程度。當r<0時，說明兩評價指標呈負相關，兩者的變化關系呈相反趨勢；反之，兩評價指標呈正相關，兩者的變化關系具有一致性。另外，評價指標間的相關性程度可由r值的絕對值大小來評價，具體標準如表1所示。

表1 相關性程度劃分標準

1.2 預測模型的構建

隧道涌水的影響因素較多，因此，隧道涌水預測具有較強的不確定性和復雜性。傳統預測模型(如BP神經網絡、RBF神經網絡和SVM模型等)難以實現隧道涌水的準確預測，并且具有如下缺點：

1)BP神經網絡的收斂速度較慢，造成訓練時間較長，且易出現局部極值的問題；

2)RBF神經網絡對大樣本預測具有訓練時間長及易出現局部極值的問題；

3)SVM模型對懲罰函數的要求較高，當該值選擇不當時，易出現過擬合現象。

極限學習機是近些年新興起的一種新型智能預測算法，具有學習速度快、泛化能力強等優點，可有效克服局部極值等問題。因此，本文將其作為隧道涌水預測模型的理論基礎。極限學習機(extreme learning machine,ELM)是一種單層前饋神經網絡，包含3層網絡結構，若樣本表示為(xi，ti，i=1,2,…,N)，N為樣本總數，則ELM模型的訓練過程可表示為

(2)

式中：yj為預測值；L為隱層節點數；βi為隱層與輸出層間的連接權值；g(x)為激勵函數；wi為輸入層與隱層間的連接權值；xj為輸入值；bi為隱層神經元閾值。

通過ELM模型的不斷訓練，可實現誤差的零逼近，即

(3)

進而可將ELM模型的訓練過程表示為

(4)

將式(4)轉變為矩陣形式，即為

T=Hβ。

(5)

式中：T為輸出矩陣；H為隱層矩陣；β為權值矩陣。

值得指出的是，受各種誤差因素的綜合影響，任一模型均不可能完全刻畫預測對象，即式(5)在應用過程中是不嚴格相等的，會存在一定誤差。誤差矩陣的表達形式為

V=T-Hβ。

(6)

式中V為誤差矩陣。

1.3 ELM模型相關問題優化

根據相關系數法的影響因素篩選，可有效保證輸入層信息的有效性。但通過ELM模型原理分析可知，ELM模型在應用過程中仍存在3個問題： 1)激勵函數的選擇問題； 2)隱層神經元的個數問題； 3)誤差矩陣的弱化問題。

為取得隧道涌水的高精度預測，仍需進一步優化上述3個問題。結合相關文獻[8-9]的研究成果，上述3個問題的優化方法如下。

1.3.1 激勵函數的優化

ELM模型共有3種激勵函數，分別為Hardlim型、Sine型和Sigmiod型。各類激勵函數的適用性存在一定差異，難以直接判斷其在工程應用中的有效性。因此，本文提出采用全試算的方法來確定最優激勵函數，即對3種激勵函數的預測效果進行試算，將預測效果最優者作為最優激勵函數。

1.3.2 隱層節點數的優化

隱層節點數對ELM模型的預測精度具有較大影響，主要表現為： 節點數較少時難以保證預測精度，反之，又有可能出現過擬合現象。目前，并沒有隱層節點數的直接確定方法，多是根據一定的經驗公式綜合確定。為解決隱層節點數的優化問題，本文先利用經驗公式確定隱層節點數的經驗值，再對其進行區間擴展，驗算不同節點數的預測效果，進而確定出最優隱層節點數。根據文獻[10]的研究成果，隱層節點數的經驗公式可由式(7)進行求解，即

(7)

式中：m、n分別為輸入層和輸出層的節點數；a為調節常數，一般取10。

上述激勵函數和隱層節點數的優化均屬于ELM模型的參數優化。結合兩者的優化方法及預測過程，將兩者的優化順序設計為： 先利用經驗公式確定隱層節點數的經驗值，然后以經驗值作為初步隱層節點數，并對3類激勵函數進行預測試算，以確定最優激勵函數，最后再對最優隱層節點數進行篩選求解。為便于后期描述，將該階段優化后的模型命名為參數優化ELM模型。

1.3.3 誤差值的弱化

預測結果的誤差值是不可避免的，但可對其進行一定程度的弱化，以提高預測精度。為實現該目的，本文利用M估計弱化誤差值，其準則為

(8)

通過求導及最小二乘估計可實現式(8)的轉換，即將誤差值的弱化問題轉變為權值矩陣β的求解問題，進而得到M估計條件下ELM模型的權值矩陣

β=(HTPH)-1HTPT。

(9)

式中P為權函數矩陣。

在式(9)的求解過程中，M估計是通過迭代計算實現的。其過程為： 根據誤差值的大小，對不同觀測值賦予不同的權重，再通過反復迭代計算弱化觀測值的權重，進而達到弱化誤差的目的。

M估計的優化過程主要是對預測誤差進行弱化。因此，該優化過程是位于激勵函數和隱層節點數優化之后，且為便于后期描述，將該階段的優化模型命名為R-ELM優化模型。

2 工程實例分析

2.1 工程概況

通海隧道為玉蒙線的重點工程，起始里程DK27+060，出口里程DK37+362，長度為10.302 km，最大埋深約467 m，屬于特長深埋鐵路隧道。該隧道位于高原構造剝蝕溶蝕低中山地貌，多為北東向山脈，高程為1 560～2 203 m，高差一般為100～643 m，相對起伏較大；同時，斜坡地帶植被以松林為主，局部為灌木，總體植被較為發育，而溝谷平緩地帶則多為旱地，局部為水田。根據野外調查及鉆孔勘探可知，隧址區地層巖性較為復雜，其中，第四系覆土以粉質黏土、塊石土和泥炭質土為主，共分為8類土層，但各類土層對隧道涌水災害的影響較小。

結合區域地質資料和鉆孔成果，隧址區基巖以D3zg、Zbd、C1、C2+3灰巖和白云巖為主，且各類可溶性巖石隧道長度占隧道全長的90%，多呈灰色、灰白色，厚層—中厚層狀，質堅性脆，完整性較差。受場區內大構造背景影響，區內褶皺及斷裂構造較為發育，共計有4處褶皺和4條斷裂帶，造成巖體松動，且地下水補給徑流條件較好，使得隧道發生涌水災害的可能性較大。因此，開展該隧道的涌水災害研究具有較強的必要性[11-12]。

2.2 隧道涌水災害影響因素分析

通海隧道所處地質條件較為復雜，隧道涌水災害受多種因素綜合作用影響。由工程實際及文獻[6-7]可知，隧道涌水發生需要巖性條件、構造條件及地下水循環條件等共同作用。因此，可將隧道涌水影響因素細分為巖石可溶性影響因素、地表匯水影響因素、地質構造影響因素、地下水循環影響因素和隧道空間位置影響因素等。為實現隧道涌水的高精度預測，結合通海隧道的工程實際，將上述5類因素的選取標準和量化標準分述如下。

2.2.1 巖石可溶性因素

巖石可溶性是巖溶發育的必要條件之一，其決定了后期溶穴的儲水能力。結合以往的研究成果可知，可溶性影響因素主要包含2個方面： 1)可溶鹽的礦物成分因素，一般條件下，碳酸巖的不溶物含量不應超過10%，因此可利用可溶鹽(CaCO3)的含量來評價巖溶的發育程度，即CaCO3的含量越高，巖溶的發育程度越高，富水性也越強。2)巖石結構因素，該影響因素可控制地下水的徑流條件，且結合工程實際，可進一步將該因素細分為微觀結構因素和宏觀結構因素，其中，微觀結構因素可由巖石結構類型進行劃分，而宏觀結構因素可由隧道圍巖級別進行劃分。

為便于后續預測分析，有必要將上述各因素進行量化處理。結合工程實際，將巖石可溶性因素的量化標準劃分，如表2所示。

表2巖石可溶性因素的量化劃分標準

Table 2 Quantitative classification criteria for rock solubility factors

CaCO3含量/%巖石結構圍巖級別量化評分 <5粗晶結構Ⅰ0～525～5亮晶結構Ⅱ5～1050～25粒屑結構Ⅲ10～1575～50泥晶結構Ⅳ15～20 >75生物碎屑結構Ⅴ20～25

2.2.2 地表匯水影響因素

地表水的匯集是隧道涌水災害發生的補給條件，即地表水的匯水條件越好，隧址區地下水的補給條件相對也越好，進而發生涌水災害的可能性也越大。因此，隧道涌水災害的發生與地表匯水影響因素具有較大的聯系。結合工程實際，將地表匯水影響因素劃分為3類，即降雨量、地形地貌及滲透系數。其中，降雨量是地下水的直接來源；地形地貌則決定了地表水的匯聚能力，即地形坡度越陡，降雨越易形成地表徑流，地下水的補給條件相對越差，反之，地下水的補給條件相對越好；滲透系數直接關系地表水的下滲能力。類比巖石可溶性因素的量化過程，將地表匯水影響因素也進行量化處理，其中，降雨量因素可直接由降雨量進行歸一化處理得到量化值，滲透系數以可用類比的統計方法進行量化處理。地形地貌因素的量化劃分標準如表3所示。

表3地形地貌因素的量化劃分標準

Table 3 Quantitative classification criteria for topographic and geomorphic factors

地形坡度/(°)量化評分>450～430～454～820～308～1210～2012～16<1016～20

2.2.3 地質構造因素

地質構造直接控制著地下水的水力聯系，進而影響涌水災害發生時的水量補給。因此，地質構造是涌水災害發生的另一重要影響因素。結合區域地質構造可知，隧址區主要位于單斜構造中，其巖層組合關系、巖層厚度和巖層傾角會對涌水災害產生直接影響。因此，將上述3個指標作為地質構造因素的二級指標。在實際量化過程中，3個指標均是通過統計位置掌子面的具體參數進行量化。地質構造因素的量化劃分標準見表4。

表4地質構造因素的量化劃分標準

Table 4 Quantitative classification criteria for geological structural factors

地質構造因素分類量化評分巖層組合關系孔隙-裂隙巖溶含水組0～4夾層裂隙含水組4～10厚層脈狀-裂隙含水組10～16厚層裂隙-巖溶含水組16～20巖層厚度薄層狀 0～2中厚層狀2～6厚層狀6～10巨厚層狀10～12巖層傾角>60°0～660°～45°6～1045°～30°10～14<30°14～20

2.2.4 地下水循環影響因素

地下水的循環運動是巖溶發育的必要條件之一，其循環過程具有多種運動特征。地下水循環程度一般可由Ca+含量來決定，即利用該離子在水中的飽和指數SIC來確定，SIC值越小，說明地下水的溶蝕能力越強，反之，溶蝕能力越弱。同時，涌水段的長度也可反映地下水的循環強度，涌水段長度越大，地下水循環條件相對越好。在量化過程中，涌水段長度指標可由現場施工直接測得，因此，以其現場監測值作為統計指標；飽和指數則是基于現場取樣后的室內試驗求得，且在工程實際應用過程中，若未取得研究斷面的水樣，可將距離其最近的飽和指數SIC試驗結果作為指標進行預測研究。飽和指數SIC的量化劃分標準如表5所示。

2.2.5 隧道空間位置影響因素

由于隧道洞身位置的埋深不一致，因此，其所處位置的垂直向分帶也具有一定差異，且由于不同垂向分帶對巖溶發育具有較大的影響，因此，以隧道所處的循環帶類型來評價隧道空間位置對涌水災害的影響。隧道所處循環帶指標的量化劃分標準如表6所示。在具體量化過程中，以隧道勘察成果為基礎，通過統計斷面的里程進行位置確定，再以現場涌水條件作為校核依據，以確定隧道所處循環帶的量化評分。

表5飽和指數SIC的量化劃分標準

Table 5 Quantitative classification criteria for saturation index SIC

飽和指數SIC量化評分 >1.20～41.2～0.84～80.8～0.48～120.4～0 12～16<016～20

表6隧道所處循環帶指標的量化劃分標準

Table 6 Quantitative classification criteria for cyclic zones index in tunnels

隧道所處循環帶量化評分水平徑流帶18～14深部徑流帶12～8交替帶12～6垂直滲流帶6～0

通過上述總結分析，將通海隧道的涌水影響因素共分為5大類12小類，具體如表7所示。

表7通海隧道涌水影響因素統計

Table 7 Statistics of influencing factors of water inflow in Tonghai Tunnel

前述各評價指標的量化評分有一定差異，不利于后續預測模型的構建，因而有必要利用式(10)進行無量綱處理，以提高數據的均衡性。

(10)

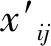
本文以DK29+203斷面為例，詳述各影響因素的量化過程。圍巖CaCO3含量為30%，根據表2得其評分為11分；圍巖為粒屑結構，評分為12分；圍巖級別為Ⅳ級，評分為20分；對應地形坡度為30°～45°，評分為7分；巖層組合關系為厚層脈狀-裂隙含水組地下水，評分為15分；巖層厚度為中厚層狀，評分為5分；巖層傾角為35°，評分為12分；Ca+的飽和指數SIC為0.6，評分為10分；隧道所處循環帶為深部徑流帶，評分為10分。根據上述評分量化，再利用式(10)進行歸一化處理，得到隧道涌水災害樣本量化評分如表8所示。

通海隧道在施工過程中發生了多起涌水災害事故，為更好地指導類似工程，基于前述影響因素分析，統計了17處現場涌水災害樣本，如表8所示。

2.3 隧道涌水影響因素的篩選

隧道涌水影響因素較多，共有5個一級影響因素和12個二級影響因素，不同影響因素對隧道涌水災害的作用程度存在一定差異。為保證后續預測模型輸入層的可靠性，有必要對影響因素進行篩選處理。本文利用相關系數法篩選各影響因素對隧道涌水災害的影響程度，篩選結果如表9所示。各影響因素與涌水量間的相關系數存在不同，因此，各影響因素對隧道涌水災害的影響程度也有差異。根據篩選結果統計，呈負相關的影響因素共計有4個，所占比例為33.33%，說明各影響因素多以正相關為主；地形地貌因素、巖層傾角因素和涌水段長度的相關程度相對較低，所占比例為25%；Ⅱ級影響因素共有7個，所占比例為58.33%，而Ⅲ級影響因素僅2個，所占比例為16.66%，說明影響因素的相關性等級以Ⅱ級為主。

值得指出的是，在分析結果中，降雨量、涌水段長度與涌水量間存在負相關，這與工程實際存在一定差異。

降雨量與涌水量呈負相關原因： 1)降雨入滲至隧道所處位置需要一定的時間，造成降雨入滲的效果存在一定差異； 2)降雨不僅影響地下水系統，還與地表水系統相關，且兩系統間也存在著復雜的水力聯系，因此其影響規律存在一定差異。

表8 隧道涌水災害影響因素歸一化處理后的樣本統計

表9隧道涌水影響因素篩選統計

Table 9 Screening statistics of influencing factors of tunnel water inflow

序號影響因素相關系數相關性相關程度相關等級1巖性化學成分-0.258負相關中度相關Ⅱ2巖石結構0.326正相關中度相關Ⅱ3圍巖級別0.363正相關中度相關Ⅱ4降雨量-0.345負相關中度相關Ⅱ5地形地貌0.132正相關低度相關Ⅰ6滲透系數0.533正相關高度相關Ⅲ7巖層組合類型0.275正相關中度相關Ⅱ8巖層厚度-0.239負相關中度相關Ⅱ9巖層傾角0.124正相關低度相關Ⅰ10涌水段長度-0.096負相關低度相關Ⅰ11方解石0.360正相關中度相關Ⅱ12隧道所處循環帶0.461正相關高度相關Ⅲ

涌水段長度與涌水量呈負相關原因： 從某種程度上講涌水段越長，對應的涌水量應越高，但這忽略了每延米上是平均涌水速率的影響，即涌水可能存在于短距離上的集中涌水，也可能存在于長距離上的少量滲水等；同時，該因素與涌水量間的相關性也較弱，不僅說明了該因素對隧道涌水的影響程度有限，也驗證了該文影響因素篩選的必要性。

雖然上述兩影響因素與工程實際存在一定差異，但本文僅是以影響因素相關性程度來確定預測模型的輸入層信息，因此，影響因素的相關性對預測模型的影響有限，其相關性程度才是預測模型輸入層信息構建的決定因素。

根據上述影響因素的篩選結果，本文以相關等級為Ⅱ級和Ⅲ級的影響因素作為后續預測模型的輸入層，即輸入層共計有9個神經網絡節點。

2.4 隧道涌水的預測分析

根據前述預測模型的構建過程，以1—12號樣本作為訓練樣本，13—17號樣本作為驗證樣本，并將參數優化過程和誤差值弱化過程分述如下。

2.4.1 參數優化過程

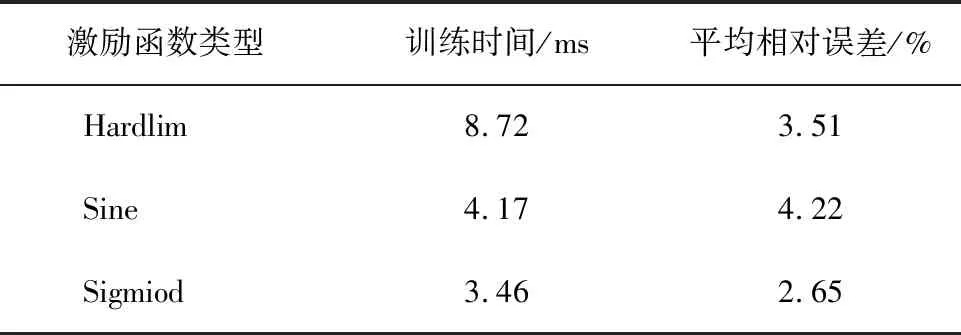
根據前述影響因素篩選，得出涌水預測模型的輸入層共計有9個網絡節點，而輸出層為涌水量，具有1個網絡節點，進而確定初步隱層節點數為13，并以該隱層節點數進行初步設置，試算得到各激勵函數的預測效果如表10所示。在訓練時間方面，Hardlim型激勵函數的訓練時間相對最長，其次是Sine型激勵函數和Sigmiod型激勵函數；而在預測精度方面，Sigmiod型激勵函數的平均相對誤差最小，預測精度最優，其次是Hardlim型激勵函數和Sine型激勵函數。因此，不同激勵函數在該文實例中的適用性具有明顯差異，在對比訓練時間和預測精度的基礎上，確定Sigmiod型激勵函數的預測效果相對最優。

表10不同激勵函數的預測效果

Table 10 Statistics of predicted effects of different excitation functions

激勵函數類型訓練時間/ms平均相對誤差/%Hardlim8.723.51Sine4.174.22Sigmiod3.462.65

在最優激勵函數的基礎上，再對隱層節點數進行優化篩選，篩選區間為9—17，結果如表11所示。根據隱層節點數的優化篩選可知，隨隱層節點數的增加，訓練時間也會有一定程度的增加，說明隱層節點數并非越多越好； 同時，隨隱層節點數的增加，樣本的平均累計誤差和平均相對誤差均呈現先減小再增加的趨勢，且當隱層節點數為14時，平均相對誤差僅為2.28%，預測結果相對最優。

根據上述參數優化，綜合確定ELM模型的最優激勵函數為Sigmiod型，隱層節點數為14。

2.4.2 誤差值弱化

在參數優化的基礎上，再利用M估計進一步弱化預測誤差。為驗證本文預測模型及M估計的有效性，同步利用傳統BP神經網絡進行預測，并將參數優化和M估計優化后的預測結果進行對比分析，結果如表12所示。

表11不同隱層節點數的預測結果統計

Table 11 Statistics of predicted results for number of nodes in different hidden layers

隱層節點數訓練時間/ms平均累計誤差/(m3/d)平均相對誤差/%91.21326.953.95102.43281.543.73112.81261.293.53123.02248.133.12133.46202.152.65143.83174.162.28154.92199.122.55167.66247.782.821710.24255.453.04

對比不同預測模型在相應驗證樣本處的預測結果可知，ELM模型的預測精度均不同程度地高于傳統BP神經網絡模型，驗證了ELM模型作為新型智能算法的優越性。同時，對比M估計優化前后的預測結果可知，通過M估計的誤差弱化，各驗證樣本的相對誤差均出現不同程度減小，說明M估計能達到弱化預測誤差的目的。R-ELM模型的相對誤差均值為1.12%，說明該模型具較高的預測精度，適用于隧道涌水預測。

表12 不同預測模型的隧道涌水預測結果統計

綜上所述，R-ELM模型具有較快的運算速度和精度，對隧道涌水預測的適用性較好，值得在類似工程項目中的推廣應用研究。

3 結論與討論

通過相關系數法和R-ELM模型在通海隧道涌水預測中的綜合應用研究，主要獲得了如下結論。

1)巖溶隧道的涌水影響因素較多，共有5個一級影響因素和12個二級影響因素，且不同影響因素與涌水量之間的相關性多以中度相關為主。

2)在預測模型的構建過程中，激勵函數類型和隱層節點數對預測效果具有較大的影響，利用試算法可有效實現參數優化，對保證預測精度具有重要意義；同時，M估計可有效弱化誤差值，可進一步提高預測精度。

3)本文構建的R-ELM模型具有較高的預測精度，且其泛化能力較強，適用于隧道涌水預測。本文的隧道涌水量預測思路也可應用于類似工程的涌水災害防治。

4)由于隧道所處環境具有明顯的區域性特征，隧道涌水災害的影響因素也存在一定差異，因此，在R-ELM模型的推廣應用中，應充分結合工程實際，構建合適的隧道涌水影響因素評價體系，以保證預測模型輸入層信息的準確性。