大跨PC連續(xù)剛構橋主梁關鍵設計參數影響分析

摘要：為研究大跨PC連續(xù)剛構橋主梁不同設計參數對結構受力的影響，文章以某98 m+180 m+ 98 m大跨PC連續(xù)剛構橋為工程背景，選取了主梁邊中跨比、梁底曲線冪次、跨中梁高和支點梁高4個關鍵設計參數，分別分析了不同設計參數主梁在自重作用下的內力、應力及最大撓度變化情況，得出了主梁不同設計參數對結構受力的影響程度，為大跨PC連續(xù)剛構橋主梁在參數選取與截面設計方面提供一定的參考與借鑒。

關鍵詞：連續(xù)剛構橋;主梁;設計參數;邊中跨比;梁底曲線冪次;跨中梁高;支點梁高

中圖分類號：U448. 23文獻標識碼：A DOI： 10. 13282/j. cnki. wccst.2019. 12. 036

文章編號：1673 - 4874（2019）12 - 0131 - 06

0 引言

大跨PC連續(xù)剛構橋憑借其受力合理、行車舒適、施工方便、跨越能力大等優(yōu)點在我國橋梁建設中得到了廣泛的應用[1]。然而由于大跨PC連續(xù)剛構橋設計參數眾多，受力復雜，在參數選取與截面設計中受設計人員工作經驗影響，往往存在一些因參數設計不合理而導致橋梁病害發(fā)生的問題[2-4]。

為研究大跨PC連續(xù)剛構橋主梁不同設計參數對結構受力的影響，近年來，國內學者對此作了不少研究。文獻[5]對主梁自重、混凝土收縮徐變、溫度、主梁彈模等進行了不同程度的參數敏感性分析，研究發(fā)現(xiàn)主梁自重、混凝土收縮徐變、溫度等因素為主梁主要敏感性參數，主梁彈模為次要敏感性參數。文獻[6]也做了類似的參數分析。文獻[7、8]則以某連續(xù)剛構橋為工程背景，分析了梁底曲線變化對主梁受力狀態(tài)的影響。

本文在以上研究的基礎上，以某98 m+ 180 m+ 98 m大跨PC連續(xù)剛構橋為工程背景，選取主梁邊中跨比、梁底曲線冪次、跨中梁高和支點梁高4個關鍵設計參數，分別分析不同設計參數主梁在自重作用下的內力、應力及跨中最大撓度的變化情況，為大跨PC連續(xù)剛構橋主梁在參數選取與截面設計方面提供一定的參考與借鑒。

1 工程背景簡介及原始模型建立

1.1 工程背景簡介

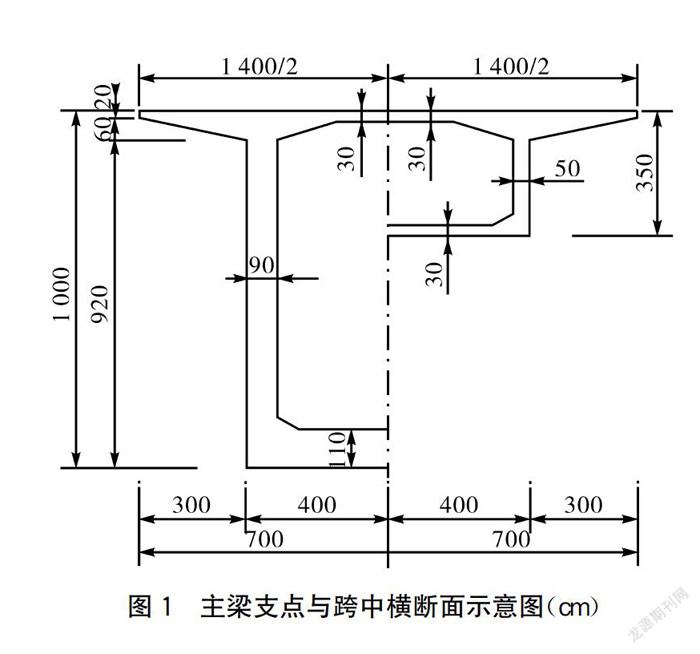
本橋為三跨PC連續(xù)剛構橋，橋跨布置為98 m+ 180 m+ 98 m，上構主梁為單箱單室箱梁，其支點與跨中橫斷面如下頁圖1所示。箱梁底部曲線冪次采用1.7次，采用懸臂現(xiàn)澆施工，主梁采用C55混凝土。下構采用雙肢薄壁墩，橫橋向壁寬8m，順橋向壁厚1.8m，雙肢中心間距為7.8m，墩身采用C40混凝土，基礎均采用樁基礎。

1.2 原始模型建立

采用Midas Civil 2019軟件建立結構整體有限元模型（如圖2所示）。全橋共劃分為202個梁單元，其中上構11 2個梁單元，下構90個梁單元。

2 不同邊中跨比主梁受力影響分析

經國內外統(tǒng)計表明，大跨PC連續(xù)剛構橋主梁邊中跨比大部分在0. 55～0. 58之間，故本文分別選取邊跨長94 m、98 m、102 m、106 m、110 m五組參數，保持中跨180 m不變，則五組參數的邊中跨比分別為0. 522、0.544、0.566、0.588、0.611。根據選取的五組參數，分別建立結構有限元模型，分析不同邊中跨比主梁在自重作用下的內力、應力及邊跨最大撓度的變化情況。

2.1 自重作用下主梁內力分析

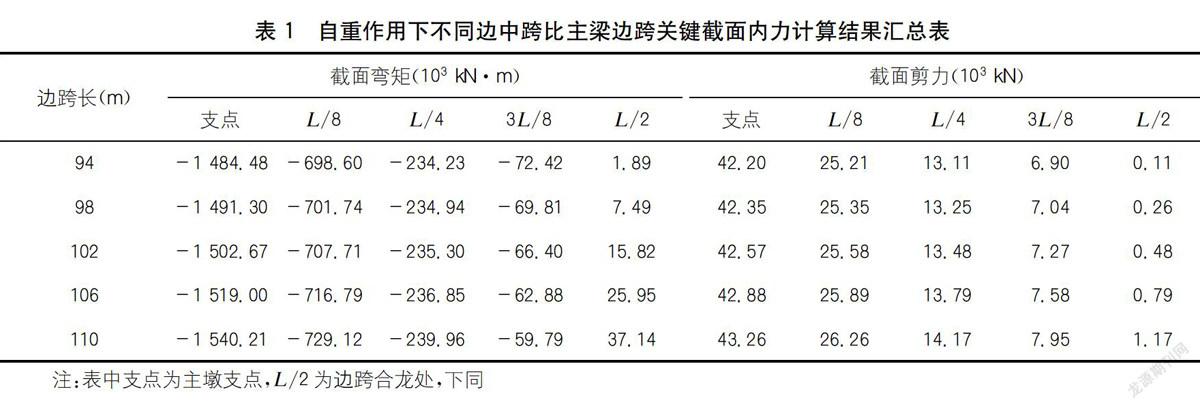
自重作用下不同邊中跨比主梁邊跨關鍵截面內力有限元計算結果如表1所示。

分析表1可知：自重作用下主梁邊跨支點、L/8、L/4、L/2截面彎矩隨邊中跨比增大而增大，3L/8截面彎矩隨邊中跨比增大而減小，邊中跨比越大，變化速率越快，離L/4截面越近，變化速率越緩。

自重作用下主梁邊跨截面剪力隨邊中跨比增大而增大，邊中跨比越大，變化速率越快，離//4截面越近，變化速率越緩。

2.2 自重作用下主梁應力分析

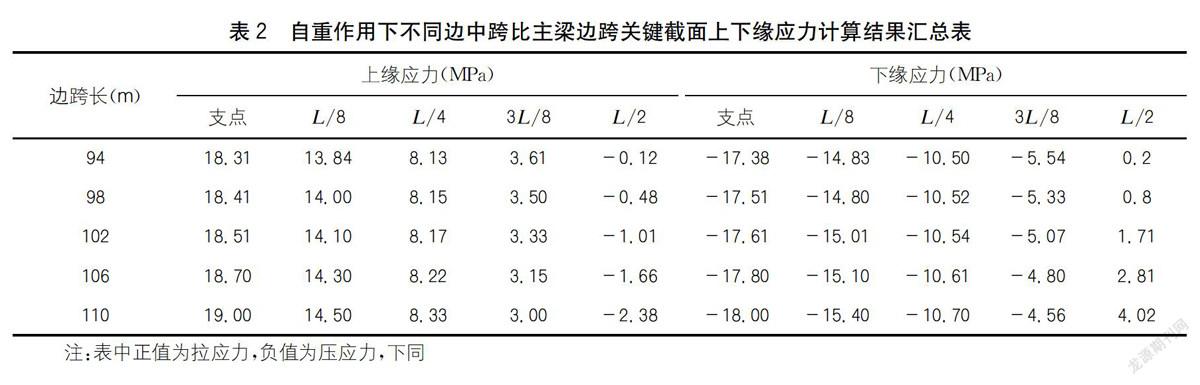
自重作用下不同邊中跨比主梁邊跨關鍵截面上下緣應力有限元計算結果如表2所示。

分析表2可知：自重作用下主梁應力變化與彎矩類似，邊跨支點、L/8、L/4、L/2截面上下緣應力隨邊中跨比增大而增大，3//8截面上下緣應力隨邊中跨比增大而減小，離L/4截面越近，變化速率越緩。

2.3 自重作用下主梁邊跨最大撓度分析

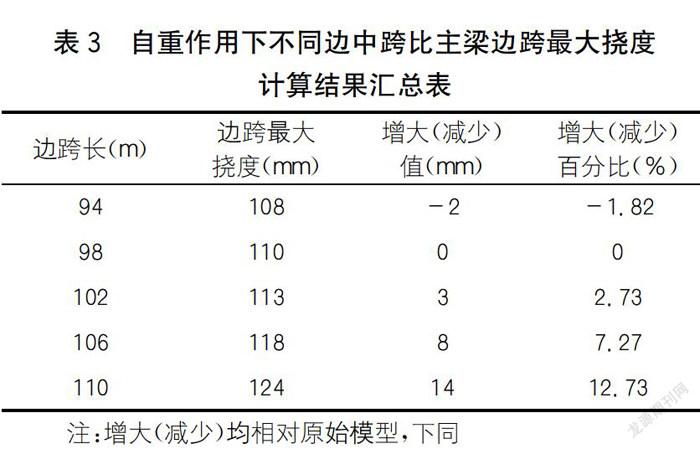
自重作用下不同邊中跨比主梁邊跨最大撓度有限元計算結果如表3所示。

分析表3可知：自重作用下主梁邊跨最大撓度隨邊中跨比增大而增大，邊中跨比越大，變化速率越快。

3 不同梁底曲線冪次主梁受力影響分析

經國內外統(tǒng)計表明，大跨PC連續(xù)剛構橋主梁梁底曲線冪次大部分在1.6～2.0O之間，故本文選取梁底曲線冪次1.6、1.7、1.8、1.9、2.0五組參數。根據選取的五組參數，分別建立結構有限元模型，分析不同梁底曲線冪次主梁在自重作用下的內力、應力及跨中最大撓度的變化情況。

3.1 主梁自重變化分析

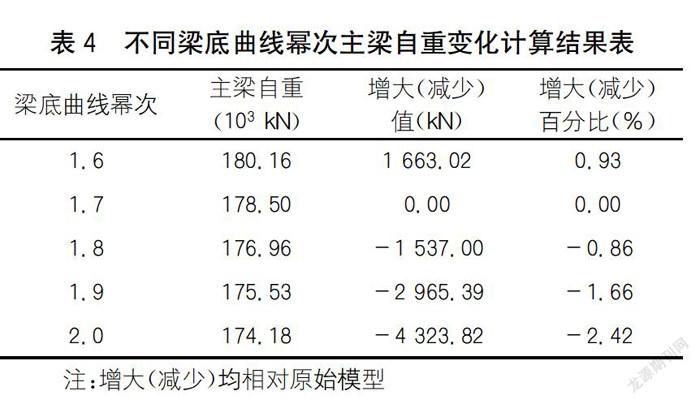
不同梁底曲線冪次主梁自重計算結果如表4所示。

分析表4可知：主梁自重隨梁底曲線冪次增大而減少，但減少百分比不大，變化規(guī)律接近線性。若單從混凝土方量考慮，梁底曲線冪次對主梁經濟性影響較小。

3.2 自重作用下主梁內力分析

自重作用下不同梁底曲線冪次主梁關鍵截面內力有限元計算結果如表5所示。

分析表5可知：自重作用下主梁截面內力隨梁底曲線冪次增大而減少，梁底曲線冪次越大，變化速率越緩，離支點越近，變化幅度越大，變化速率越快。

3.3 自重作用下主梁應力分析

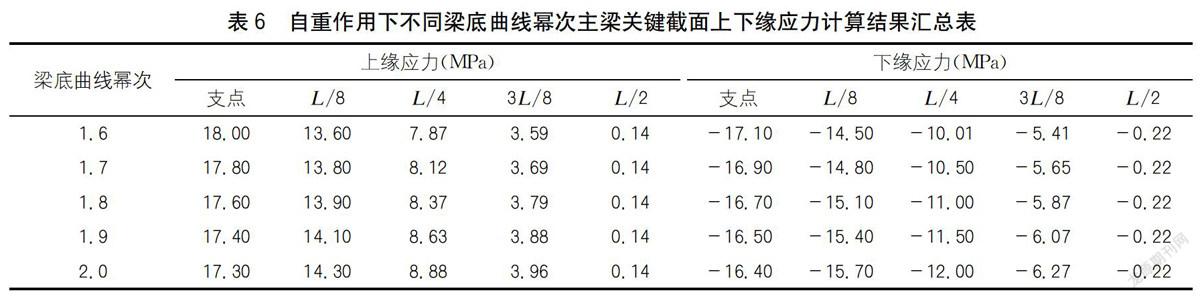
自重作用下不同梁底曲線冪次主梁關鍵截面上下緣應力有限元計算結果如表6所示。

分析表6可知：自重作用下主梁支點截面應力隨梁底曲線冪次增大而減少，L/8、L/4、3L/8截面應力隨梁底曲線冪次增大而增大，L/2截面應力幾乎無變化。截面應力變化最大為主梁L/4截面，尤其是下緣應力變化。由此可見，梁底曲線冪次是影響主梁L/4截面應力變化的一個重要因素。

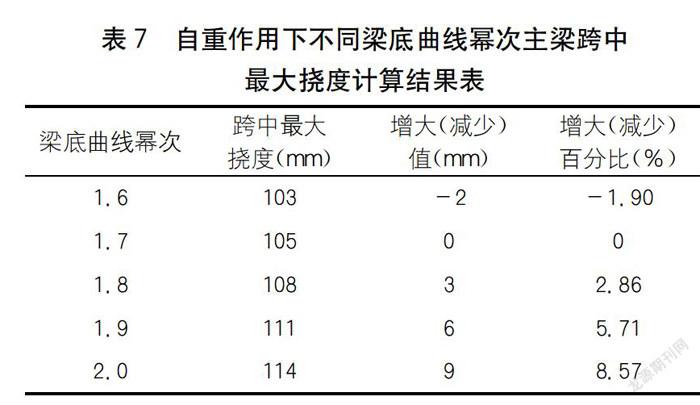
3.4 自重作用下主梁跨中最大撓度分析

自重作用下不同梁底曲線冪次主梁跨中最大撓度有限元計算結果如表7所示。中梁高與中跨之比大部分在1/50～1/60之間，故本文選取跨中梁高3.00 m、3.25 m、3.50 m、3.75 m、4. 00 m五組參數，保持中跨180 m不變，則五組參數與中跨之比分別為1/60.0、1/55. 4、1/51.4、1/48.0、1/45.0。根據選取的五組參數，分別建立結構有限元模型，分析不同跨中梁高主梁在自重作用下的內力、應力及跨中最大撓度的變化情況。

4.1 主梁自重變化分析

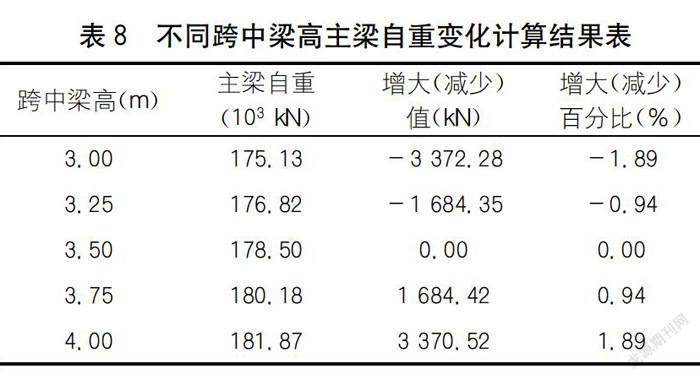
不同跨中梁高主梁自重計算結果如表8所示。

分析表7可知：自重作用下主梁跨中最大撓度隨梁底曲線冪次增大而增大，變化規(guī)律接近線性。

4不同跨中梁高主梁受力分析

經國內外統(tǒng)計表明，大跨PC連續(xù)剛構橋主梁跨

分析表8可知：主梁自重隨跨中梁高增大而增大，但增大百分比有限，變化規(guī)律接近線性。同樣，若單從混凝土方量考慮，跨中梁高對主梁經濟性影響較小。

4.2 自重作用下主梁內力分析

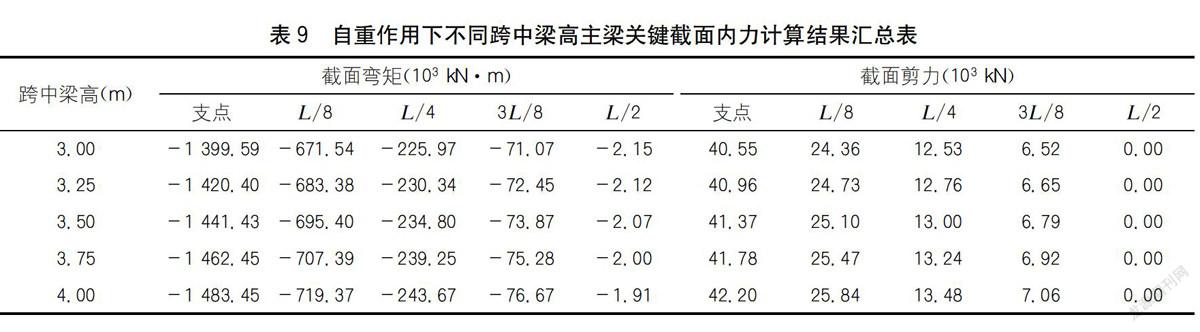
自重作用下不同跨中梁高主梁關鍵截面內力有限元計算結果如表9所示。

分析表9可知：自重作用下主梁截面內力隨跨中梁高增大而增大，離支點越近，變化幅度越大，變化規(guī)律接近線性。

4.3 自重作用下主梁應力分析

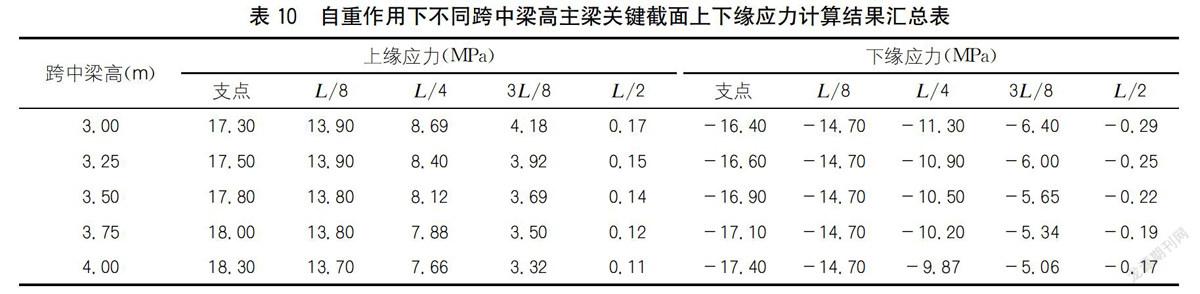
自重作用下不同跨中梁高主梁關鍵截面上下緣應力有限元計算結果如表10所示。

分析表10可知：自重作用下主梁支點截面應力隨跨中梁高增大而增大，應力變化較明顯，L/8、//4、3L/8、L/2截面應力隨梁高增大而減少，L/4及3L/8截面應力變化最明顯。由此可見，跨中梁高是影響主梁L/4及3L/8截面應力變化的一個重要因素。

4.4 自重作用下主梁跨中最大撓度分析

自重作用下不同跨中梁高主梁跨中最大撓度有限元計算結果如表11所示。

分析表11可知：自重作用下主梁跨中最大撓度隨跨中梁高增大而減少，變化甚微。

5 不同支點梁高主梁受力分析

經國內外統(tǒng)計表明，大跨PC連續(xù)剛構橋主梁支點梁高與中跨之比大部分在1/17～1/20之間，故本文選取支點梁高9.00 m、9.50 m、10.00 m、10. 50 m、11.00 m五組參數，保持中跨180 m不變，則五組參數與中跨之比分別為1/20.0、1/18.9、1/18.O、1/17.1、1/16.3。根據選取的五組參數，分別建立結構有限元模型，分析不同支點梁高主梁在自重作用下的內力、應力及跨中最大撓度的變化情況。

5.1 主梁自重變化分析

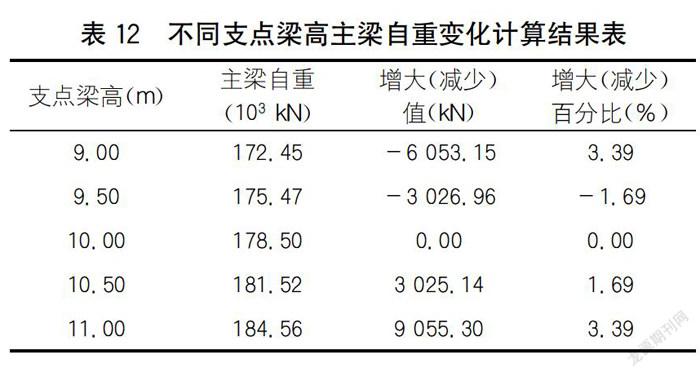
不同支點梁高主梁自重計算結果如表12所示。

分析表12可知：主梁自重隨支點梁高增大而增大，但增大百分比有限，變化規(guī)律接近線性。同樣，若單從混凝土方量考慮，支點梁高對主梁經濟性影響較小。

5.2 自重作用下主梁內力分析

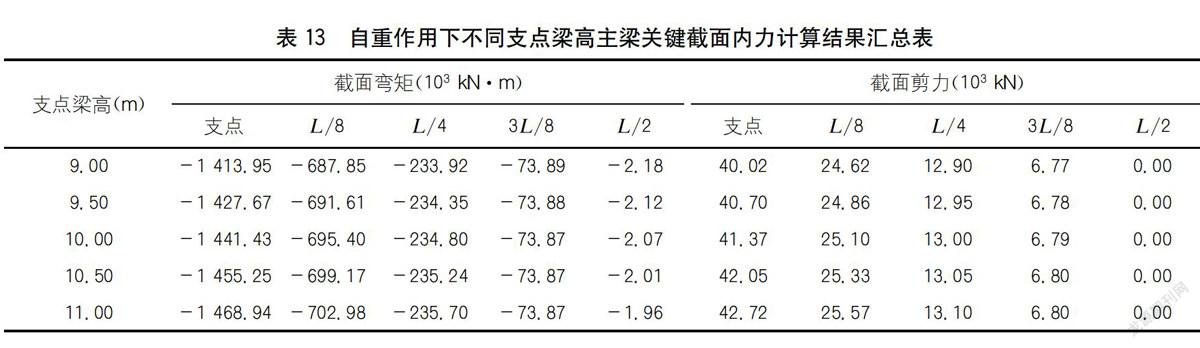
自重作用下不同支點梁高主梁關鍵截面內力有限元計算結果如表13所示。

分析表13可知：自重作用下主梁截面內力隨支點梁高增大而增大，離支點越近，變化幅度越大，變化規(guī)律接近線性。

5.3 自重作用下主梁應力分析

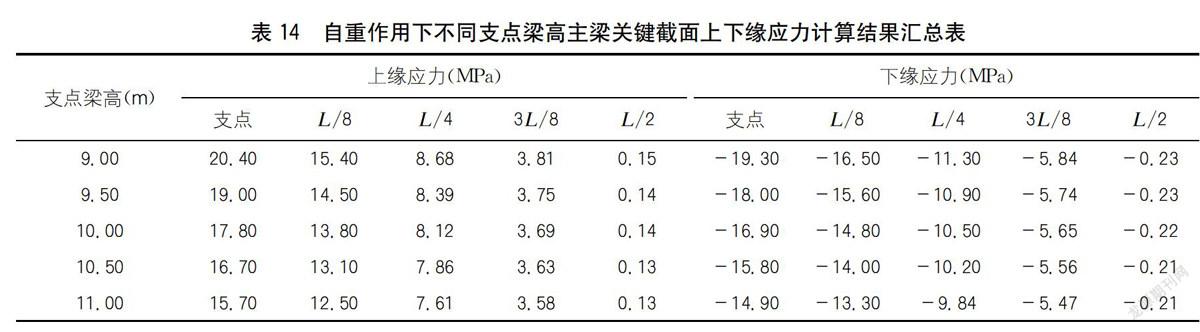
自重作用下不同支點梁高主梁關鍵截面上下緣應力有限元計算結果如表14所示。

分析表14可知：自重作用下主梁截面應力隨支點梁高增大而減少，支點梁高越大，變化速率越緩，離支點越近，變化幅度越大，變化速率越快，支點及L/8截面應力變化最明顯。由此可見，支點梁高是影響主梁支點及L/8截面應力變化的一個重要因素。

5.4 自重作用下主梁跨中最大撓度分析

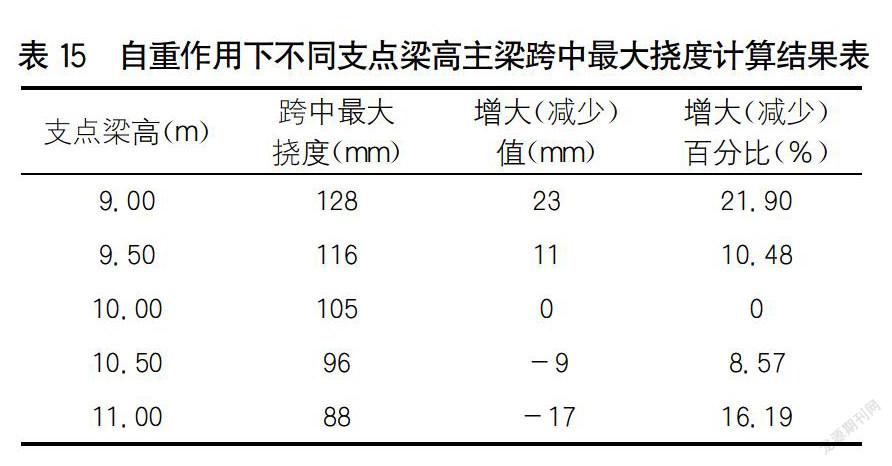
自重作用下不同支點梁高主梁跨中最大撓度有限元計算結果如表15所示。

分析表15可知：自重作用下主梁跨中最大撓度隨支點梁高增大而減少，支點梁高越大，變化速率越緩。

6 結語

大跨PC連續(xù)剛構橋不同設計參數對結構受力影響有所不同。主梁自重作用下，邊中跨比對主梁邊跨L/4截面受力影響最小，離L/4截面越遠，受力影響越大;梁底曲線冪次對主梁L/4截面受力影響最大，對跨中截面影響最小;跨中梁高對主梁L/4及3L/8截面受力影響較大，對L/8截面影響最小;支點梁高則對主梁支點及L/8截面受力影響較大，對跨中截面影響最小。此外，梁底曲線冪次、跨中梁高、邊中跨比對主梁自重作用下最大撓度影響有限，支點梁高對主梁最大撓度影響較大。

因此，在大跨PC連續(xù)剛構橋主梁設計中，若因截面設計不合理而導致主梁驗算難以滿足規(guī)范要求[9-10]（或所計算儲備值偏小）時，根據不合理截面位置，應有針對性地調整主梁對應設計參數，修改設計截面，能快速將主梁調整到合理的受力狀態(tài)。該思路已在實橋設計中得以應用，應用效果良好。

參考文獻

[1]姚玲森.橋梁工程[M].北京：人民交通出版社，2008.

[2]常興科.大跨徑連續(xù)剛構橋不合理邊中跨比的調整[J].公路，2009（10）：26 - 29.

[3]劉慶志.PC連續(xù)剛構橋箱梁下緣曲線選取研究[J].山西建筑，2008（15）：11-13.

[4]白蓉蓉.大跨度預應力混凝土連續(xù)剛構橋設計參數研究[D].西安：長安大學，2011.

[5]劉龍，呂吳文，劉釗.大跨度連續(xù)剛構橋參數敏感性分析[J].內蒙古公路與運輸，2018（5）：54 - 58.

[6]劉雪鋒，文武.某大跨度連續(xù)剛構橋參數影響分析[J].公路與汽運，2012（4）：195 -198.

[7]付雷，沈兆坤，周旭.小跨徑連續(xù)剛構橋梁底曲線研究[J].公路交通科技應用技術版，2015（7）：125-127.

[8]張才平，金東，童曉鵬.大跨混凝土連續(xù)剛構梁底曲線合理形式研究[J].交通科技，201 0，238（1）：24 - 26.

[9]JTG D60-2015，公路橋涵設計通用規(guī)范[S]。

[10]JTG 3362 - 2018，公路鋼筋混凝土及預應力混凝土橋涵設計規(guī)范[S].

作者簡介：張維軍（1987-），工程師，主要從事公路工程施工和管理工作。