頻率捷變相控陣雷達最大似然測角方法
(西安電子科技大學雷達信號處理國家重點實驗室,陜西西安 710071)
0 引 言
頻率捷變技術可以大大提高雷達的抗干擾能力與戰場生存能力[1-5],因此國內外軍用雷達常采用頻率捷變體制。為了能在戰爭中獲得主動權,要求雷達必須能夠準確估計敵方目標的方向。在陣列信號處理中,目標角度估計方法有很多,如波束形成、子空間類算法[6-7]和最大似然算法[8]等。頻率捷變雷達通常采用脈間頻率捷變技術,相鄰發射脈沖的載頻會在較寬頻段內快速變化,使得目標相鄰回波去相關,且相鄰脈沖信噪比起伏嚴重[9],因此頻率捷變雷達進行目標角度估計性能較差,只有想辦法將頻率捷變雷達的多次不相干快拍數據進行合理有效的積累,才能提高測角精度。
目前,頻率捷變雷達進行角度估計時可以采用二進制積累方式或者非相干積累的方式對多次快拍進行處理[10],這兩種方式都是基于最大似然算法的。二進制積累即先對每一次快拍數據進行角度估計,得到一組角度估計值,然后對這組角度估計值進行取平均操作,這種處理方式只是簡單取平均,因此性能依然很差。非相干積累方法即采用最大似然算法對多次快拍數據直接進行處理,建立起代價函數,通過使代價函數最大化來估計目標角度,該方法只是對多次快拍數據的簡單利用,因此對測角性能的提高有限,尤其是當信噪比較低時,測角精度依然較差。
針對上述問題,本文提出一種頻率捷變相控陣雷達最大似然測角方法,該方法對每一次快拍數據分別進行角度估計,得到一組角度估計值,然后利用多次快拍的測角精度得到一組最優融合的權值,用該組權值對多次角度估計結果進行融合得到新的角度估計值。該方法充分挖掘了多次快拍數據的有效信息,能夠有效地提高測角精度,在低信噪比時測角精度依然能得到一定提升,具有實際工程意義。
1 信號模型
設陣列為一個由N個陣元組成的均勻線陣,陣元間距為d,θt為目標回波方向,λ為雷達波長,由于在相同方位上同一距離單元內存在兩個目標的情況很少發生,因此,本文假設陣列模型為單目標模型,并對陣列接收到的信號進行M次快拍采樣,則M次快拍的接收數據可以表示為
x(m)=Smam(θt)+n(m),m=1,2,…,M
(1)
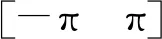
am(θt)表示第m次快拍時目標信號的導向矢量,此導向矢量與每次快拍數據的載頻有關,其表達式可以寫為
(2)
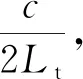
n(m)表示零均值的高斯白噪聲,與信號不相關。
2 頻率捷變相控陣雷達最大似然測角方法
2.1 基本原理
對于頻率捷變相控陣雷達,每次快拍都可獲得一個角度估計值,但是由于各次快拍間的信噪比起伏很大,導致這一組角度估計值的估計精度也相差較大。該算法從測角精度出發,在對角度信息進行融合時應該根據測角精度來優化權值,如果該次快拍的測角精度高,則該次快拍角度估計值對應的權值大,反之,精度低的角度估計值對應的權值小,因此可以根據多次快拍數據的信息得到一組最優權值使得融合后的角度估計值精度達到最高。具體過程如下:
首先,對每一次快拍進行角度估計,設第m次快拍時的掃描波束導向矢量矩陣為
(3)
式中,Θ為雷達作用空域角度集合,為了表示方便,將Am(Θ)簡記為Am,am(θt)簡記為am,x(m)簡記為xm。利用權矢量Am對M次快拍數據分別進行常規波束形成,求得M次快拍數據的似然函數分別為
(4)
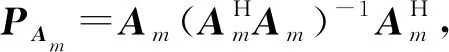
(5)
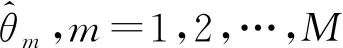
(6)
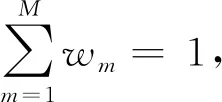
2.2 單次快拍下最大似然算法的理論精度分析
最優權值的選取與各次快拍的測角精度密切相關,為了便于最優權值的計算,在本小節對單次快拍時最大似然算法角度估計的偏差和方差理論值進行推導,本文推導的理論前提為每次測角的誤差服從零均值的高斯分布,由于篇幅受限,這里省略了推導過程,具體可參考文獻[11]。
在上述信號模型下,當信噪比足夠大時,單次快拍最大似然算法測角偏差和方差分別為
(7)
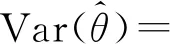
[σ2/|s|2+(N)-1σ4/|s|4]*
(8)
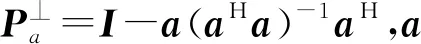
上式中的角度估計方差為兩部分之和,隨著陣元數或陣元信噪比|s|2/σ2的增大,兩部分趨于零,但第二部分趨于零的速度要遠快于第一部分。因此在陣元數或信噪比足夠大的情況下,單次快拍時最大似然算法的角度估計理論均方誤差為
(9)
(10)
式中,f為當前快拍雷達信號的載頻,k為一固定常數,與陣元個數、陣元間距、目標方向有關,k值并不影響后面最優權值的計算。
2.3 最優融合加權
M次快拍得到的M個角度估計值之間彼此相互獨立,由2.2節可得M個角度估計值的偏差和方差為
(11)
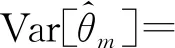
(12)

(13)
(14)
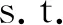
(15)
wm≥0,m=1,2,…,M
對上述優化問題進行求解,得到最優權
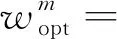
m=1,2,…,M
(16)
用此最優權值對M個角度估計值進行加權獲得的目標角度估計值,此時可保證測角誤差最小。

至此,可得到最優融合權值:
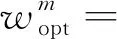
m=1,2,…,M
(17)
從式(16)可以看出,本算法中的權系數是由每一次快拍的雷達信號載頻和檢測信噪比來決定的,該加權融合方式物理意義明確,信噪比越大的快拍數據對應的角度測量值可靠性越高,因此權重越大。本方法充分挖掘出了多次快拍數據的有效信息,并對其進行綜合利用,因此可以明顯提高測角精度,且在信噪比很低的情況下測角精度依然能得到一定的提升。
3 計算機仿真
為了驗證文中方法的有效性,作如下仿真。
仿真參數:假設回波信號模型為SwerlingⅡ或Swerling Ⅳ,陣列結構為均勻線陣,陣元個數N=16,陣元間距d=0.05 cm,初始載頻f0=3×109Hz,任意兩次快拍數據的載頻頻差為15 MHz,目標角度為10°,蒙特卡洛實驗次數為1 000次,噪聲功率采用長度為2 000的實際樣本進行估計。
實驗1:積累快拍數為10,信噪比變化區間為-6~12 dB,分別利用二進制積累、非相干積累和最優融合的方法對目標角度進行估計,當回波模型為SwerlingⅡ時,得到3種方法均方根誤差隨信噪比變化的對比圖如圖1所示,當回波模型為Swerling Ⅳ時,3種方法均方根誤差隨信噪比變化的對比圖如圖2所示。
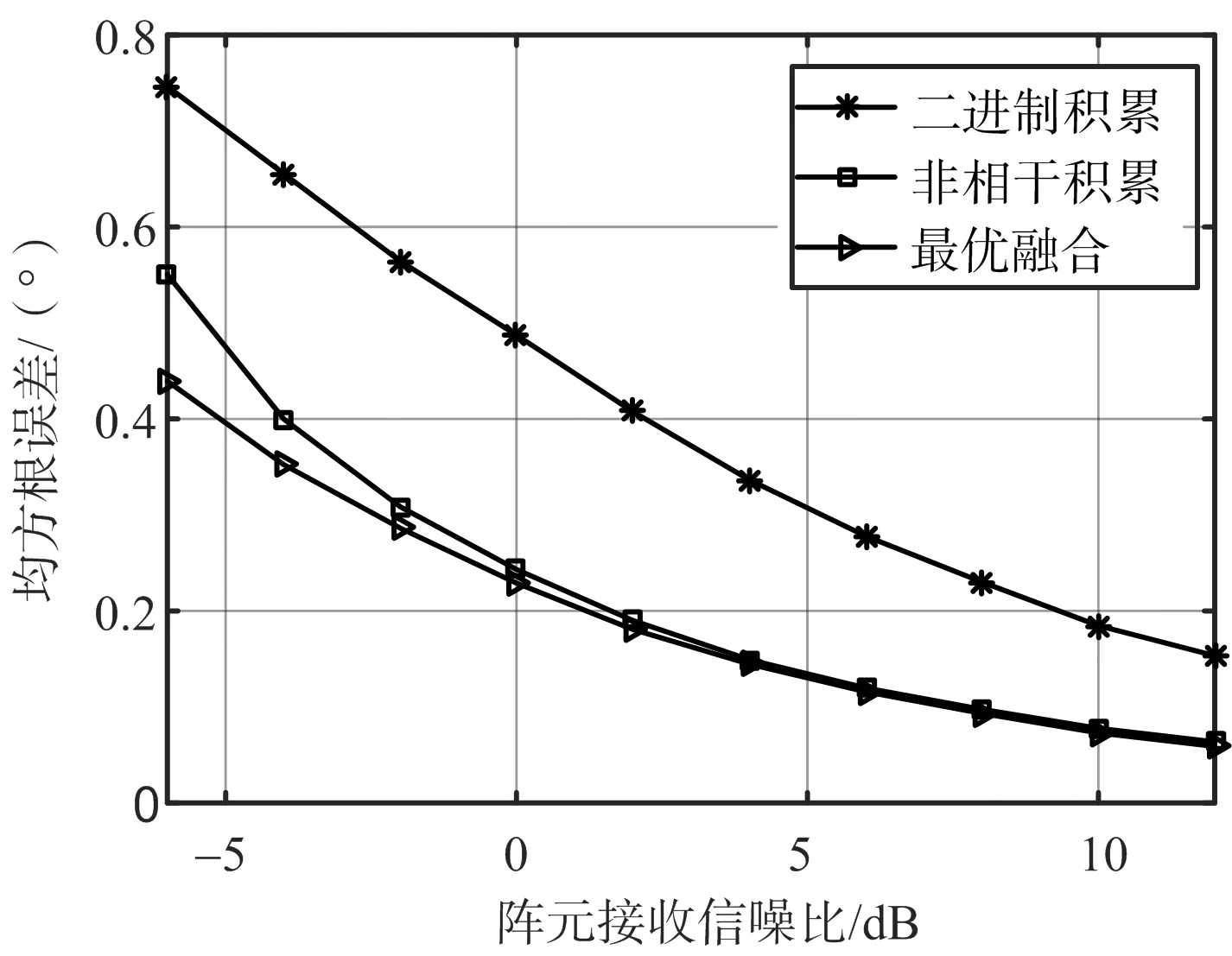
圖1 RMSE隨信噪比變化圖(SwerlingⅡ模型)
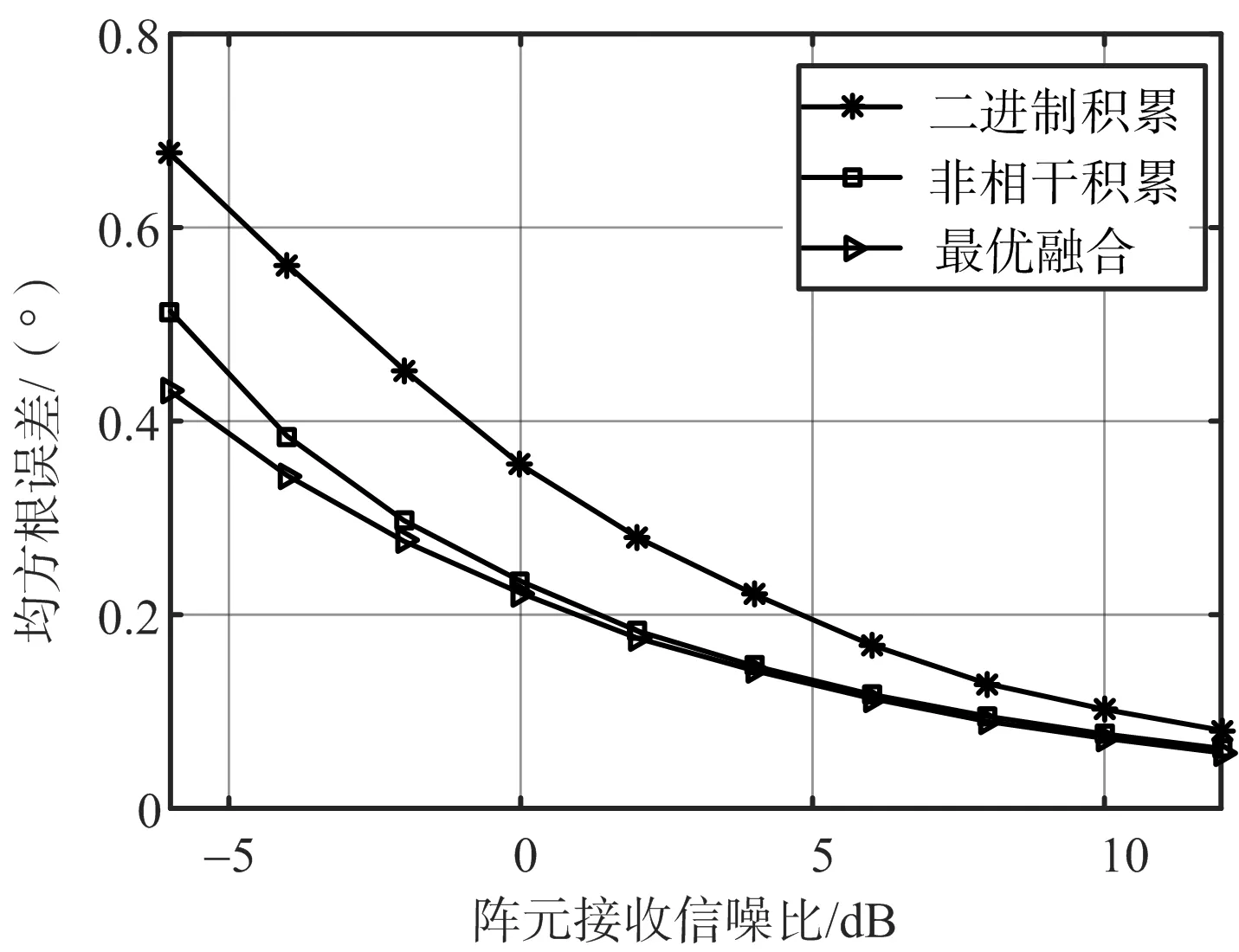
圖2 RMSE隨信噪比變化圖(Swerling Ⅳ模型)
實驗2:單次快拍陣元信噪比為-5 dB,積累快拍數變化范圍為1~10,分別利用二進制積累、非相干積累和最優融合的方法對目標角度進行估計,當回波模型為Swerling Ⅱ時,可得3種方法的均方根誤差隨積累快拍數變化的對比圖如圖3所示,當回波模型為Swerling Ⅳ時,3種方法的均方根誤差隨積累快拍數變化的對比圖如圖4所示。
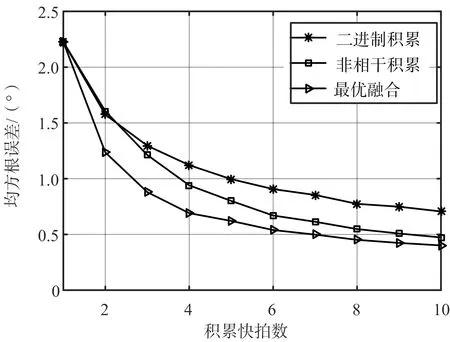
圖3 RMSE隨快拍數變化圖(Swerling Ⅱ模型)
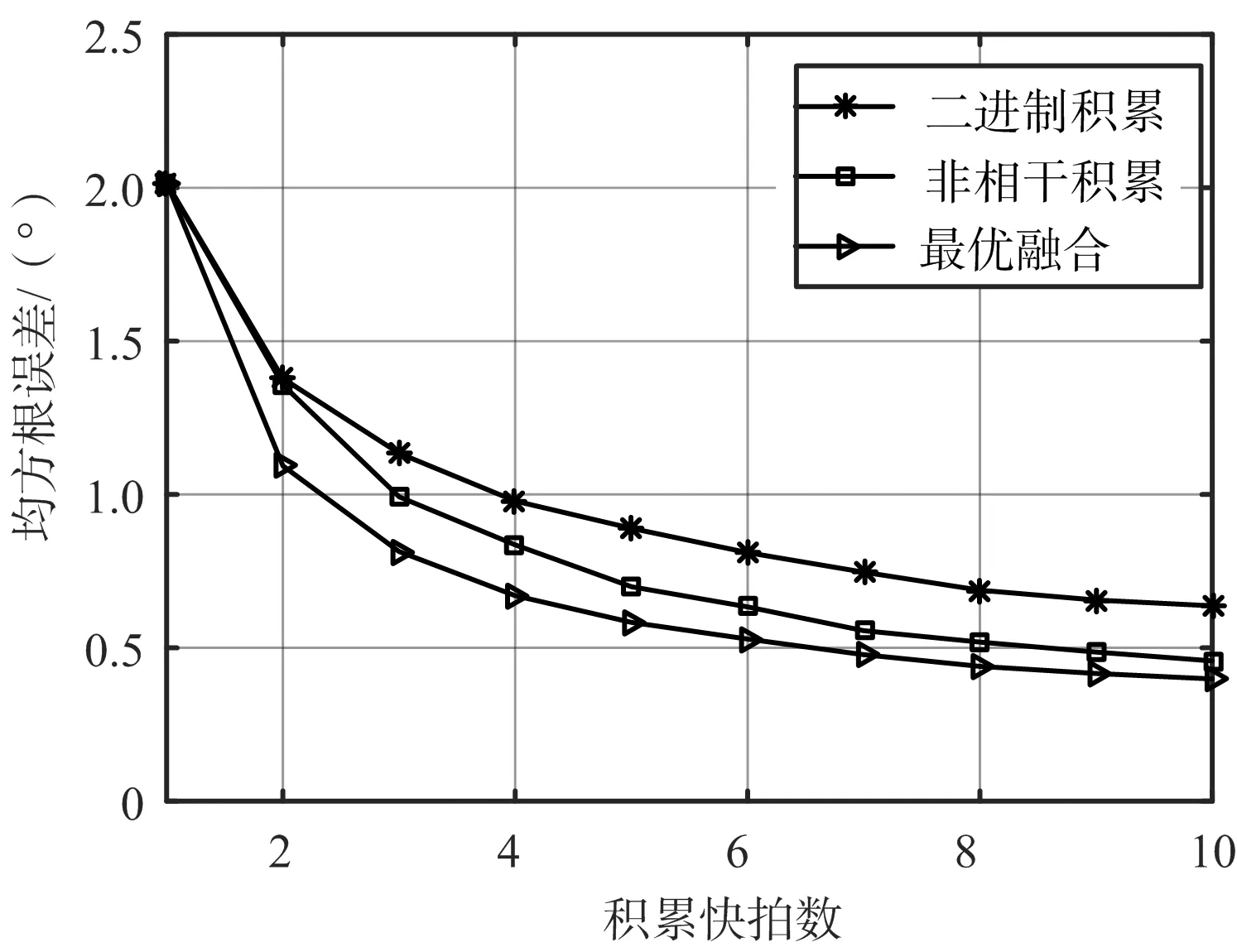
圖4 RMSE隨快拍數變化圖(Swerling Ⅳ模型)
由圖1、圖2可以看出,隨著信噪比的增大,3種方法的測角均方根誤差都逐漸減小,即測量精度隨著信噪比的增大而提高,但是最優融合方法的測角誤差始終最小,即使在信噪比較小時,該方法依然是有效的。由圖3、圖4的對比可以看出,當只有單次快拍時,3種方法是等效的,但是只要積累快拍數為多次(大于一次)時,最優融合方法的測角精度就高于另外兩種方法。
4 結束語
本文提出了一種頻率捷變相控陣雷達最大似然測角方法,該方法利用最優融合的思想充分有效地將多次不相關的快拍數據積累起來,提高了頻率捷變相控陣雷達的測角性能,即使在信噪比較低的情況下測角精度也能得到一定程度的提升。仿真結果表明,此方法具有一定優越性,對頻率捷變相控陣雷達測角的工程實現有一定的指導意義。

